人教A版高中数学选择性必修第一册2.4.2圆的一般方程 课件(共83张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册2.4.2圆的一般方程 课件(共83张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:44:18 | ||
图片预览











文档简介
(共83张PPT)
人教版2019高一数学(选修一) 第二章 直线和圆的方程
2.4.2 圆的一般式方程
学习目标
1.理解圆的一般方程及其特点,发展数学抽象和数学建模的核心素养。
2.掌握圆的一般方程和标准方程的互化。发展逻辑推理,直观想象、数学运算的核心素养。
3.会求圆的一般方程以及与圆有关的简单的轨迹方程问题.提升数形结合及方程思想,发展逻辑推理,直观想象、数学抽象和数学运算的核心素养。
情景导入
我们已经学习了曲线与方程的关系,也已经认识了直线方程的多种形式,
刚刚学习了圆的标准方程,现给出一个一般的二元二次方程:
Ax2+Cy2+Dx+Ey+F=0(A,C,D,E,F为常数),
请问你能写出一个它分别表示
①直线;②圆;③y关于x的二次函数的必要条件吗
1.圆的一般式方程
新知探究
根据上节课所学的知识,我们知道方程(x-1)2+(y+2) 2=4表示以(1, -2)为圆心 , 2为半径的圆 . 可以将此方程变形为
x2+y2-2x+4y+1=0.
一般地 , 圆的标准方程 (x-a)2+(y-b)2=r2可以变形为
x2+y2+Dx+Ey+F=0 的形式.
那么形如x2+y2+Dx+Ey+F=0的方程一定能通过恒等变形变为圆的标准方程吗
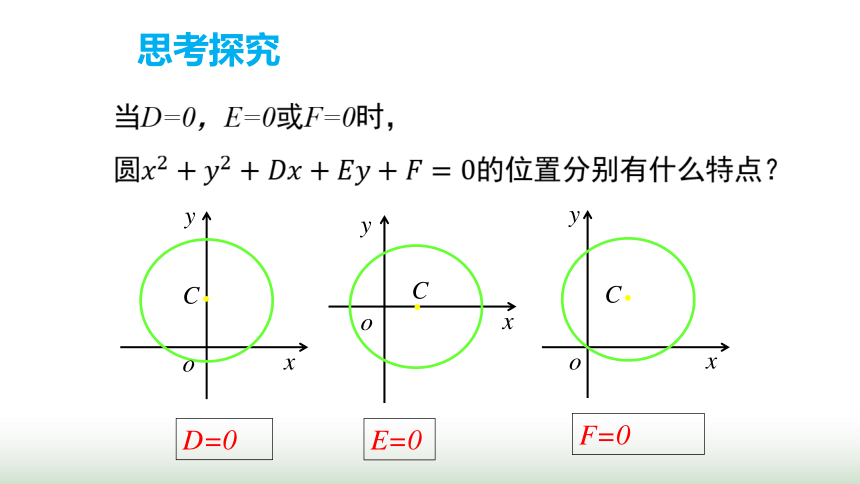
思考探究
思考探究
那么形如x2+y2+Dx+Ey+F=0的方程一定能通过恒等变形变为圆的标准方程吗
例如:对于方程x2+y2-2x-4y+6=0 ,
我们对其进行配方 , 得到(x-1)2+(y-2) 2=-1 ,
显然任意一个点的坐标(x, y)都不满足这个方程 ,
所以这个方程不表示任何图形 .
因此形如x2+y2+Dx+Ey+F=0的方程不一定能通过恒等变形变为圆的标准方程。
这表明x2+y2+Dx+Ey+F=0不一定是圆的方程。
思考探究
那么当x2+y2+Dx+Ey+F=0中的D,E,F满足什么条件时这个方程表示圆?
因此,当 D2+E2-4F>0 时,方程x2+y2+Dx+Ey+F=0表示一个圆,
我们把它叫做圆的一般方程.
你能说说圆的一般式方程同圆的标准式方程有何处不同吗?
圆的一般式方程同圆的标准式方程有何处不同
我们观察一下这个二元二次方程不难发现:
圆的一般方程突出了代数结构:
(1) x2和y2系数相同,都不等于0.
(2) 没有xy这样的二次项.
(3)当 D2+E2-4F>0 时,方程才表示一个圆.
圆的标准方程明确给出了圆心坐标和半径
圆的一般方程则明确表明其形式是一种特殊的二元二次方程.
两种方程的字母间的关系:
圆的一般式方程同圆的标准式方程有何处不同
C
x
o
y
C
x
o
y
C
x
o
y
D=0
E=0
F=0
思考探究
例4 求过三点O(0, 0) , M1(1, 1) , M2 (4, 2)的圆的方程, 并求这个圆的半径长和圆心坐标.
课本例题
建:建立直角坐标系
设:用坐标表示有关的量
限:限制条件
课本例题
代:进行有关代数运算
化:化简
概念归纳
求圆的方程常用的待定系数法,其大致步骤是:
1.根据题意, 选择标准方程或一般方程.
2.根据条件列出有关 a, b, r, 或 D, E, F 的方程组.
3.解出 a, b, r 或 D, E, F 代入标准方程或一般方程.
概念归纳
圆的一般方程与圆的标准方程在运用上的比较
求圆的方程时,如果由已知条件容易求得圆心坐标、
半径或需利用圆心的坐标或半径列方程的问题,
一般采用圆的标准方程,再用待定系数法求出a,b,r;
如果已知条件与圆心和半径都无直接关系,
一般采用圆的一般方程,再用待定系数法求出系数D,E,F.
概念归纳
求轨迹方程的三种常用方法
(1)直接法:根据题目条件,建立坐标系,设出动点坐标,找出动点满足的条件,然后化简、证明;
(2)定义法:当动点的运动轨迹符合圆的定义时,可利用定义写出动点的轨迹方程;
(3)代入法:若动点P(x,y)依赖于某圆上的一个动点Q(x1,y1)而运动,把x1,y1用x,y表示,再将Q点的坐标代入到已知圆的方程中,得点P的轨迹方程.
例1(1)方程x2+y2-2x+6y+1=0表示的是 ( )
A.以(1,-3)为圆心,6为半径的圆
B.以(-1,3)为圆心,6为半径的圆
C.以(1,-3)为圆心,3为半径的圆
D.以(-1,3)为圆心,3为半径的圆
(2)点M,N在圆x2+y2+kx+2y-4=0上,且点M,N关于直线x-y+1=0对称,则该圆的面积是________.
题型1 圆的一般方程的概念
典例剖析
C
9π
典例剖析
归纳总结
方程x2+y2+Dx+Ey+F=0表示圆的判断方法
(1)由圆的一般方程的定义,令D2+E2-4F>0,成立则表示圆,否则不表示圆.
(2)将方程配方后,根据圆的标准方程的特征判断.
应用这两种方法时,要注意所给方程是不是x2+y2+Dx+Ey+F=0这种形式,否则要化为这种形式再求解.
1.如果圆的方程为x2+y2+kx+2y+k2=0,那么当圆的面积最大时,圆心的坐标是________.
(0,-1)
练一练
例2.已知A(2,2),B(5,3),C(3,-1),求△ABC的外接圆的方程.
题型2 待定系数法求圆的一般方程
典例剖析
先设出圆的一般方程,根据点在圆上列方程组,解方程组求出待定系数,得外接圆方程.
解:因为△ABC的外接圆方程为x2+y2-8x-2y+12=0.
点M(a,2)在所求的圆上,故点M(a,2)的坐标满足圆的方程,
可得a2+22-8a-2×2+12=0,
即a2-8a+12=0,解得a=2或a=6.
例3.已知A(2,2),B(5,3),C(3,-1),点M(a,2)在△ABC的外接圆上,求a的值 .
典例剖析
例4.已知A(2,2),B(5,3),圆C过A,B两点且圆关于直线y=-x对称,
求圆的方程
典例剖析
待定系数法求圆的一般方程的步骤
(1)根据题意设所求的圆的一般方程为x2+y2+Dx+Ey+F=0.
(2)根据已知条件,建立关于D,E,F的方程组.
(3)解此方程组,求出D,E,F的值.
(4)将所得的值代回所设的圆的方程中,就得到所求的圆的一
般方程.
归纳总结
练一练
练一练
例5.已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.
(1)求线段AP中点的轨迹方程;
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
题型3 求动点的轨迹方程
典例剖析
解:(1)设AP的中点为M(x,y),
由中点坐标公式可知,P点坐标为(2x-2,2y).
因为P点在圆x2+y2=4上,所以(2x-2)2+(2y)2=4.
故线段AP中点的轨迹方程为(x-1)2+y2=1.
(2)设PQ的中点为N(x,y).
在Rt△PBQ中,|PN|=|BN|,
设O为坐标原点,连接ON,则ON⊥PQ.
所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
所以x2+y2+(x-1)2+(y-1)2=4.
故线段PQ中点的轨迹方程为x2+y2-x-y-1=0.
归纳总结
求与圆有关的轨迹问题的方法
(1)直接法:直接根据题目提供的条件列出方程.
(2)定义法:根据圆、直线等定义列方程.
(3)代入法:找到要求点与已知点的关系,代入已知点满足的关系式等.
提醒:注意“求轨迹”与“求轨迹方程”是不同的.
3.点P(4,-2)与圆x2+y2=4上任一点连线的中点的轨迹方程是( )
A.(x-2)2+(y+1)2=1
B.(x-2)2+(y+1)2=4
C.(x+4)2+(y-2)2=4
D.(x+2)2+(y-1)2=1
【答案】A
练一练
练一练
4.如图,经过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A,B两点,求线段AB的中点P的轨迹.
练一练
练一练
练一练
练一练
典例剖析
规范解答 求圆的一般方程
1.注意考虑问题的全面性
解决有关圆的问题时,要认真审题,注意隐含条件,如本例中点C在y轴的正半轴上,则其纵坐标大于零.
2.熟练圆的方程的设法
在求解圆的方程时,要根据不同的条件,灵活地设出圆的方程,如本例中根据条件可设出圆的一般方程,有时可设圆的标准方程,利用待定系数法求解即可.
归纳总结
1.已知圆的方程是x2+y2-2x+6y+8=0,那么经过圆心的一条直线的方程是( )
A.2x-y+1=0 B.2x+y+1=0
C.2x-y-1=0 D.2x+y-1=0
2.若点M(3,0)是圆x2+y2-8x-4y+10=0内一点,则过点M(3,0)的最长的弦所在的直线方程是( )
A.x+y-3=0 B.x-y-3=0
C.2x-y-6=0 D.2x+y-6=0
B
C
随堂练
3.如果x2+y2-2x+y+k=0是圆的方程,则实数k的取值范围是 .
4.已知圆C:x2+y2+2x+ay-3=0(a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则参数a的值为 .
-2
随堂练
课本练习
O
A
D
C
B
x
y
E
O
A
D
C
B
x
y
E
O
A
D
C
B
x
y
E
A
B
C
7.等腰三角形的顶点A的坐标是(4,2),底边一个端点B的坐标是(3,5),求另一个端点C的轨迹方程,并说明它是什么图形.
7.等腰三角形的顶点A的坐标是(4,2),底边一个端点B的坐标是(3,5),求另一个端点C的轨迹方程,并说明它是什么图形.
根据题意,等腰三角形ABC的另一个端点C在以A(4,2)为圆心,经过B(3,5)的圆上,且除去点B以及B关于A的对称点B’
O
A
M
B
x
y
阿氏圆是阿波罗尼斯圆的简称,已知平面上两点A、B,则所有满足PA/PB=k且不等于1的点P的轨迹是一个以定比m:n内分和外分定线段AB的两个分点的连线为直径的圆。这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿氏圆。
已知定点A(a,2)在圆x2+y2-2ax-3y+a2+a=0的外部,则a的取值范围为________.
易错辨析 忽视圆的条件致错
错因分析
a>2
错因分析
分层练习-基础
1.已知圆C过点M(1,1),N(5,1),且圆心在直线y=x-2上,则圆C的方程为( )
A.x2+y2-6x-2y+6=0 B.x2+y2+6x-2y+6=0
C.x2+y2+6x+2y+6=0 D.x2+y2-2x-6y+6=0
2.方程x2+y2+2ax-2y+a2+a=0表示圆,则实数a的取值范围是( )
A.a≤1 B.a<1
C.a>1 D.0A
B
分层练习-基础
3.已知圆的圆心为(-2,1),其一条直径的两个端点恰好在两坐标轴上,则这个圆的方程是( )
A.x2+y2+4x-2y-5=0 B.x2+y2-4x+2y-5=0
C.x2+y2+4x-2y=0 D.x2+y2-4x+2y=0
C
A
分层练习-基础
5.已知点E(1,0)在圆x2+y2-4x+2y+5k=0的外部,则k的取值范围是________.
6.动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为________.
7.已知圆C:x2+y2-2x+2y-3=0,AB为圆C的一条直径,点A(0,1),则点B的坐标为________.
8.若点(a+1,a-1)在圆x2+y2-2ay-4=0的内部(不含边界),则a的取值范围是________.
x2+y2=16
(2,-3)
a < 1
分层练习-基础
9.求经过三点A(1,-1),B(1,4),C(4,-2)的圆的一般方程.
分层练习-基础
10.已知圆经过点(4,2)和(-2,-6),该圆与两坐标轴的四个截距之和为-2,求圆的方程.
分层练习-巩固
11.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为( )
A.(x-2)2+(y+2)2=1 B.(x+2)2+(y-2)2=1
C.(x-2)2+(y-2)2=1 D.(x-2)2+(y-1)2=1
A
BC
分层练习-巩固
13.设A为圆C:(x-1)2+y2=1上的动点,PA是圆的切线且|PA|=1,则P点的轨迹方程是____________.
14.若点M(3,0)是圆x2+y2-8x-4y+10=0内一点,则过点M(3,0)的最长的弦所在的直线方程是________.
(x-1)2+y2=2
2x-y-6=0
分层练习-巩固
15.已知Rt△ABC的斜边为AB,且A(-1,0),B(3,0),求:
(1)直角顶点C的轨迹方程;
(2)直角边BC中点M的轨迹方程.
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
(1)当 时,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
人教版2019高一数学(选修一) 第二章 直线和圆的方程
2.4.2 圆的一般式方程
学习目标
1.理解圆的一般方程及其特点,发展数学抽象和数学建模的核心素养。
2.掌握圆的一般方程和标准方程的互化。发展逻辑推理,直观想象、数学运算的核心素养。
3.会求圆的一般方程以及与圆有关的简单的轨迹方程问题.提升数形结合及方程思想,发展逻辑推理,直观想象、数学抽象和数学运算的核心素养。
情景导入
我们已经学习了曲线与方程的关系,也已经认识了直线方程的多种形式,
刚刚学习了圆的标准方程,现给出一个一般的二元二次方程:
Ax2+Cy2+Dx+Ey+F=0(A,C,D,E,F为常数),
请问你能写出一个它分别表示
①直线;②圆;③y关于x的二次函数的必要条件吗
1.圆的一般式方程
新知探究
根据上节课所学的知识,我们知道方程(x-1)2+(y+2) 2=4表示以(1, -2)为圆心 , 2为半径的圆 . 可以将此方程变形为
x2+y2-2x+4y+1=0.
一般地 , 圆的标准方程 (x-a)2+(y-b)2=r2可以变形为
x2+y2+Dx+Ey+F=0 的形式.
那么形如x2+y2+Dx+Ey+F=0的方程一定能通过恒等变形变为圆的标准方程吗
思考探究
思考探究
那么形如x2+y2+Dx+Ey+F=0的方程一定能通过恒等变形变为圆的标准方程吗
例如:对于方程x2+y2-2x-4y+6=0 ,
我们对其进行配方 , 得到(x-1)2+(y-2) 2=-1 ,
显然任意一个点的坐标(x, y)都不满足这个方程 ,
所以这个方程不表示任何图形 .
因此形如x2+y2+Dx+Ey+F=0的方程不一定能通过恒等变形变为圆的标准方程。
这表明x2+y2+Dx+Ey+F=0不一定是圆的方程。
思考探究
那么当x2+y2+Dx+Ey+F=0中的D,E,F满足什么条件时这个方程表示圆?
因此,当 D2+E2-4F>0 时,方程x2+y2+Dx+Ey+F=0表示一个圆,
我们把它叫做圆的一般方程.
你能说说圆的一般式方程同圆的标准式方程有何处不同吗?
圆的一般式方程同圆的标准式方程有何处不同
我们观察一下这个二元二次方程不难发现:
圆的一般方程突出了代数结构:
(1) x2和y2系数相同,都不等于0.
(2) 没有xy这样的二次项.
(3)当 D2+E2-4F>0 时,方程才表示一个圆.
圆的标准方程明确给出了圆心坐标和半径
圆的一般方程则明确表明其形式是一种特殊的二元二次方程.
两种方程的字母间的关系:
圆的一般式方程同圆的标准式方程有何处不同
C
x
o
y
C
x
o
y
C
x
o
y
D=0
E=0
F=0
思考探究
例4 求过三点O(0, 0) , M1(1, 1) , M2 (4, 2)的圆的方程, 并求这个圆的半径长和圆心坐标.
课本例题
建:建立直角坐标系
设:用坐标表示有关的量
限:限制条件
课本例题
代:进行有关代数运算
化:化简
概念归纳
求圆的方程常用的待定系数法,其大致步骤是:
1.根据题意, 选择标准方程或一般方程.
2.根据条件列出有关 a, b, r, 或 D, E, F 的方程组.
3.解出 a, b, r 或 D, E, F 代入标准方程或一般方程.
概念归纳
圆的一般方程与圆的标准方程在运用上的比较
求圆的方程时,如果由已知条件容易求得圆心坐标、
半径或需利用圆心的坐标或半径列方程的问题,
一般采用圆的标准方程,再用待定系数法求出a,b,r;
如果已知条件与圆心和半径都无直接关系,
一般采用圆的一般方程,再用待定系数法求出系数D,E,F.
概念归纳
求轨迹方程的三种常用方法
(1)直接法:根据题目条件,建立坐标系,设出动点坐标,找出动点满足的条件,然后化简、证明;
(2)定义法:当动点的运动轨迹符合圆的定义时,可利用定义写出动点的轨迹方程;
(3)代入法:若动点P(x,y)依赖于某圆上的一个动点Q(x1,y1)而运动,把x1,y1用x,y表示,再将Q点的坐标代入到已知圆的方程中,得点P的轨迹方程.
例1(1)方程x2+y2-2x+6y+1=0表示的是 ( )
A.以(1,-3)为圆心,6为半径的圆
B.以(-1,3)为圆心,6为半径的圆
C.以(1,-3)为圆心,3为半径的圆
D.以(-1,3)为圆心,3为半径的圆
(2)点M,N在圆x2+y2+kx+2y-4=0上,且点M,N关于直线x-y+1=0对称,则该圆的面积是________.
题型1 圆的一般方程的概念
典例剖析
C
9π
典例剖析
归纳总结
方程x2+y2+Dx+Ey+F=0表示圆的判断方法
(1)由圆的一般方程的定义,令D2+E2-4F>0,成立则表示圆,否则不表示圆.
(2)将方程配方后,根据圆的标准方程的特征判断.
应用这两种方法时,要注意所给方程是不是x2+y2+Dx+Ey+F=0这种形式,否则要化为这种形式再求解.
1.如果圆的方程为x2+y2+kx+2y+k2=0,那么当圆的面积最大时,圆心的坐标是________.
(0,-1)
练一练
例2.已知A(2,2),B(5,3),C(3,-1),求△ABC的外接圆的方程.
题型2 待定系数法求圆的一般方程
典例剖析
先设出圆的一般方程,根据点在圆上列方程组,解方程组求出待定系数,得外接圆方程.
解:因为△ABC的外接圆方程为x2+y2-8x-2y+12=0.
点M(a,2)在所求的圆上,故点M(a,2)的坐标满足圆的方程,
可得a2+22-8a-2×2+12=0,
即a2-8a+12=0,解得a=2或a=6.
例3.已知A(2,2),B(5,3),C(3,-1),点M(a,2)在△ABC的外接圆上,求a的值 .
典例剖析
例4.已知A(2,2),B(5,3),圆C过A,B两点且圆关于直线y=-x对称,
求圆的方程
典例剖析
待定系数法求圆的一般方程的步骤
(1)根据题意设所求的圆的一般方程为x2+y2+Dx+Ey+F=0.
(2)根据已知条件,建立关于D,E,F的方程组.
(3)解此方程组,求出D,E,F的值.
(4)将所得的值代回所设的圆的方程中,就得到所求的圆的一
般方程.
归纳总结
练一练
练一练
例5.已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.
(1)求线段AP中点的轨迹方程;
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
题型3 求动点的轨迹方程
典例剖析
解:(1)设AP的中点为M(x,y),
由中点坐标公式可知,P点坐标为(2x-2,2y).
因为P点在圆x2+y2=4上,所以(2x-2)2+(2y)2=4.
故线段AP中点的轨迹方程为(x-1)2+y2=1.
(2)设PQ的中点为N(x,y).
在Rt△PBQ中,|PN|=|BN|,
设O为坐标原点,连接ON,则ON⊥PQ.
所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
所以x2+y2+(x-1)2+(y-1)2=4.
故线段PQ中点的轨迹方程为x2+y2-x-y-1=0.
归纳总结
求与圆有关的轨迹问题的方法
(1)直接法:直接根据题目提供的条件列出方程.
(2)定义法:根据圆、直线等定义列方程.
(3)代入法:找到要求点与已知点的关系,代入已知点满足的关系式等.
提醒:注意“求轨迹”与“求轨迹方程”是不同的.
3.点P(4,-2)与圆x2+y2=4上任一点连线的中点的轨迹方程是( )
A.(x-2)2+(y+1)2=1
B.(x-2)2+(y+1)2=4
C.(x+4)2+(y-2)2=4
D.(x+2)2+(y-1)2=1
【答案】A
练一练
练一练
4.如图,经过点M(-6,0)作圆C:x2+y2-6x-4y+9=0的割线,交圆C于A,B两点,求线段AB的中点P的轨迹.
练一练
练一练
练一练
练一练
典例剖析
规范解答 求圆的一般方程
1.注意考虑问题的全面性
解决有关圆的问题时,要认真审题,注意隐含条件,如本例中点C在y轴的正半轴上,则其纵坐标大于零.
2.熟练圆的方程的设法
在求解圆的方程时,要根据不同的条件,灵活地设出圆的方程,如本例中根据条件可设出圆的一般方程,有时可设圆的标准方程,利用待定系数法求解即可.
归纳总结
1.已知圆的方程是x2+y2-2x+6y+8=0,那么经过圆心的一条直线的方程是( )
A.2x-y+1=0 B.2x+y+1=0
C.2x-y-1=0 D.2x+y-1=0
2.若点M(3,0)是圆x2+y2-8x-4y+10=0内一点,则过点M(3,0)的最长的弦所在的直线方程是( )
A.x+y-3=0 B.x-y-3=0
C.2x-y-6=0 D.2x+y-6=0
B
C
随堂练
3.如果x2+y2-2x+y+k=0是圆的方程,则实数k的取值范围是 .
4.已知圆C:x2+y2+2x+ay-3=0(a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则参数a的值为 .
-2
随堂练
课本练习
O
A
D
C
B
x
y
E
O
A
D
C
B
x
y
E
O
A
D
C
B
x
y
E
A
B
C
7.等腰三角形的顶点A的坐标是(4,2),底边一个端点B的坐标是(3,5),求另一个端点C的轨迹方程,并说明它是什么图形.
7.等腰三角形的顶点A的坐标是(4,2),底边一个端点B的坐标是(3,5),求另一个端点C的轨迹方程,并说明它是什么图形.
根据题意,等腰三角形ABC的另一个端点C在以A(4,2)为圆心,经过B(3,5)的圆上,且除去点B以及B关于A的对称点B’
O
A
M
B
x
y
阿氏圆是阿波罗尼斯圆的简称,已知平面上两点A、B,则所有满足PA/PB=k且不等于1的点P的轨迹是一个以定比m:n内分和外分定线段AB的两个分点的连线为直径的圆。这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿氏圆。
已知定点A(a,2)在圆x2+y2-2ax-3y+a2+a=0的外部,则a的取值范围为________.
易错辨析 忽视圆的条件致错
错因分析
a>2
错因分析
分层练习-基础
1.已知圆C过点M(1,1),N(5,1),且圆心在直线y=x-2上,则圆C的方程为( )
A.x2+y2-6x-2y+6=0 B.x2+y2+6x-2y+6=0
C.x2+y2+6x+2y+6=0 D.x2+y2-2x-6y+6=0
2.方程x2+y2+2ax-2y+a2+a=0表示圆,则实数a的取值范围是( )
A.a≤1 B.a<1
C.a>1 D.0
B
分层练习-基础
3.已知圆的圆心为(-2,1),其一条直径的两个端点恰好在两坐标轴上,则这个圆的方程是( )
A.x2+y2+4x-2y-5=0 B.x2+y2-4x+2y-5=0
C.x2+y2+4x-2y=0 D.x2+y2-4x+2y=0
C
A
分层练习-基础
5.已知点E(1,0)在圆x2+y2-4x+2y+5k=0的外部,则k的取值范围是________.
6.动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,则动点P的轨迹方程为________.
7.已知圆C:x2+y2-2x+2y-3=0,AB为圆C的一条直径,点A(0,1),则点B的坐标为________.
8.若点(a+1,a-1)在圆x2+y2-2ay-4=0的内部(不含边界),则a的取值范围是________.
x2+y2=16
(2,-3)
a < 1
分层练习-基础
9.求经过三点A(1,-1),B(1,4),C(4,-2)的圆的一般方程.
分层练习-基础
10.已知圆经过点(4,2)和(-2,-6),该圆与两坐标轴的四个截距之和为-2,求圆的方程.
分层练习-巩固
11.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为( )
A.(x-2)2+(y+2)2=1 B.(x+2)2+(y-2)2=1
C.(x-2)2+(y-2)2=1 D.(x-2)2+(y-1)2=1
A
BC
分层练习-巩固
13.设A为圆C:(x-1)2+y2=1上的动点,PA是圆的切线且|PA|=1,则P点的轨迹方程是____________.
14.若点M(3,0)是圆x2+y2-8x-4y+10=0内一点,则过点M(3,0)的最长的弦所在的直线方程是________.
(x-1)2+y2=2
2x-y-6=0
分层练习-巩固
15.已知Rt△ABC的斜边为AB,且A(-1,0),B(3,0),求:
(1)直角顶点C的轨迹方程;
(2)直角边BC中点M的轨迹方程.
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
(1)当 时,
(2)当 时,
表示点
(3)当 时,
不表示任何图形
