人教A版高中数学选择性必修第一册2.5.2圆与圆的位置关系 课件(共101张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册2.5.2圆与圆的位置关系 课件(共101张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:48:43 | ||
图片预览







文档简介
(共101张PPT)
人教版2019高一数学(选修一) 第二章 直线和圆的方程
2.5.2 直线的点斜式方程
学习目标
1.能根据给定圆的方程,用代数法判断圆与圆的位置关系
(重难点)
2.能根据给定圆的方程,用几何法判断圆与圆的位置关系
(重点)
3.两圆相交与相切问题(易错点)
情景导入
“打水漂”游戏别名轻功水上漂、七点漂、漂瓦.人们用扁形瓦片或石片,在手上呈水平放置后,用力飞出,石片擦水面飞行,石片碰水面后弹起再飞,石片不断在水面上向前弹跳,直至沉水.
在这一过程中,石片与水面接触形成了一个个逐渐扩大的圆,这些圆在变化的过程中位置关系是怎样的
1.圆与圆的位置关系
新知探究
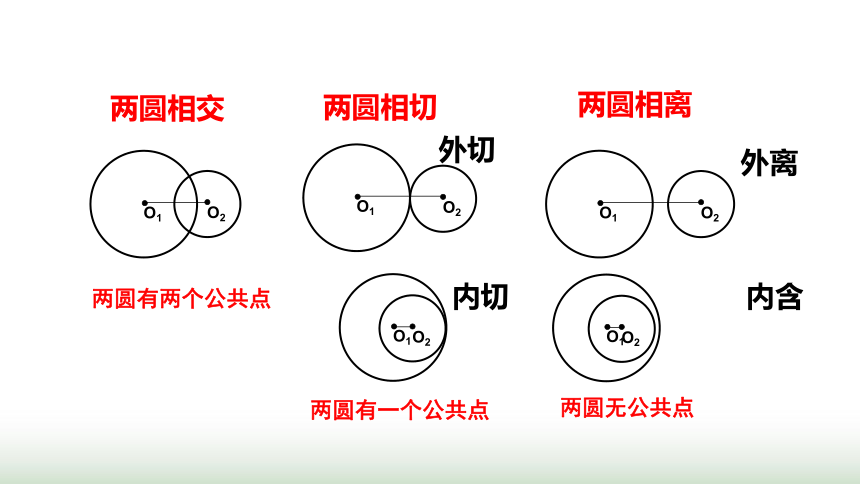
我们知道,两个圆之间存在以下三种位置关系:
(1)两圆相交,有两个公共点;
(2)两圆相切,包括外切与内切,只有一个公共点;
(3)两圆相离,包括外离与内含,没有公共点.
类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?
O1
O2
两圆相交
O1
O2
O1
O2
两圆相切
O1
O2
O1
O2
两圆相离
内切
外切
外离
内含
两圆无公共点
两圆有一个公共点
两圆有两个公共点
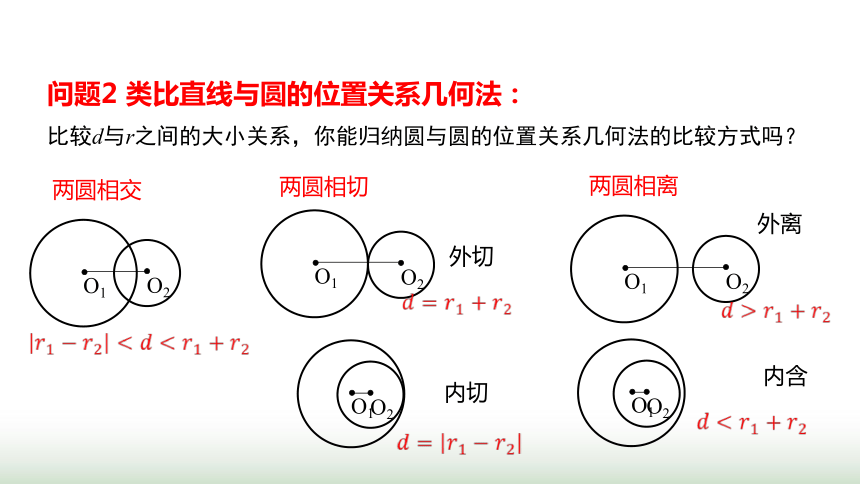
问题2 类比直线与圆的位置关系几何法:
比较d与r之间的大小关系,你能归纳圆与圆的位置关系几何法的比较方式吗?
O1
O2
两圆相交
O1
O2
O1
O2
两圆相切
O1
O2
O1
O2
两圆相离
外离
内含
外切
内切
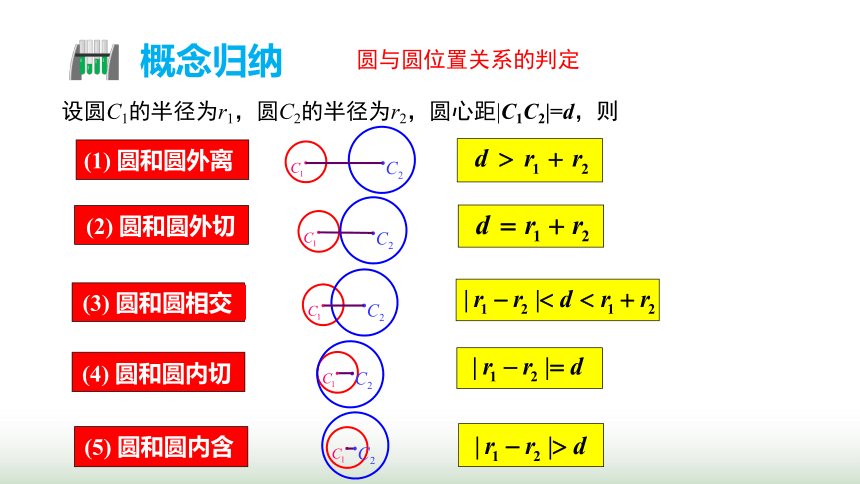
概念归纳
设圆C1的半径为r1,圆C2的半径为r2,圆心距|C1C2|=d,则
圆与圆位置关系的判定
课本例题
解法一: 把圆C1与圆C2的方程分别化成标准方程,得
∴圆C1与圆C2相交.
y
x
A
B
C2
C1
课本例题
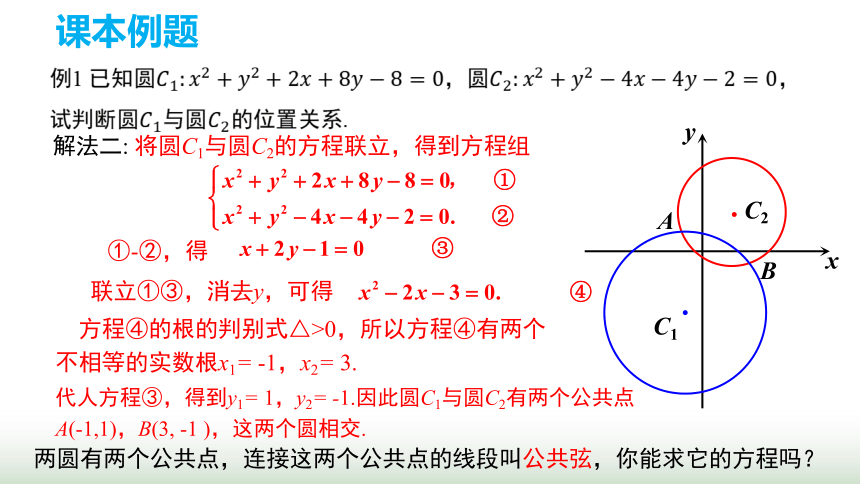
解法二: 将圆C1与圆C2的方程联立,得到方程组
①-②,得
联立①③,消去y,可得
方程④的根的判别式△>0,所以方程④有两个
不相等的实数根x1= -1,x2= 3.
y
x
A
B
C2
C1
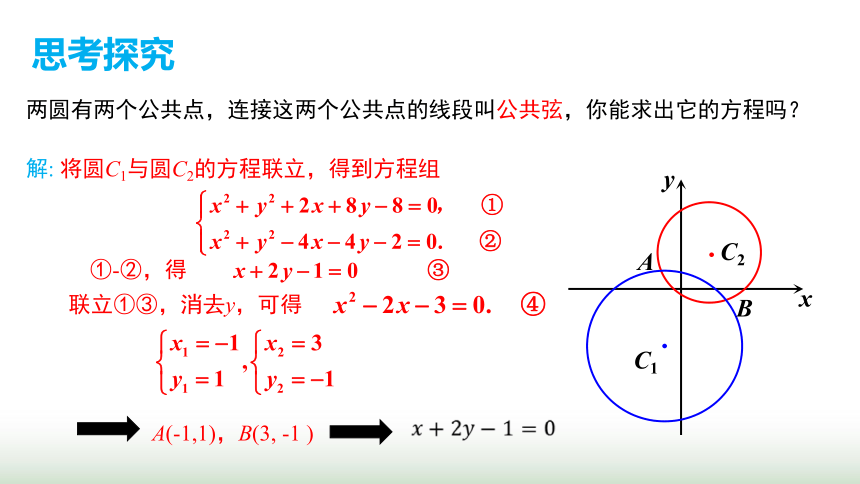
两圆有两个公共点,连接这两个公共点的线段叫公共弦,你能求它的方程吗?
代人方程③,得到y1= 1,y2= -1.因此圆C1与圆C2有两个公共点
A(-1,1),B(3, -1 ),这两个圆相交.
课本例题
解: 将圆C1与圆C2的方程联立,得到方程组
①-②,得
联立①③,消去y,可得
y
x
A
B
C2
C1
A(-1,1),B(3, -1 )
两圆有两个公共点,连接这两个公共点的线段叫公共弦,你能求出它的方程吗?
思考探究
y
x
A
B
C2
C1
A(-1,1),B(3, -1 )
消去y,可得
方法一:将圆C1与圆C2的方程联立,
方法二:将圆C1与圆C2的方程相减,得到
公共弦长的求法:
方法一:
将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
方法二:
求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
概念归纳
思考探究
思考探究
你能比较这两种方法的特征吗
几何法:直观,容易理解,可以判断两圆确切的位置关系,但不能求出交点坐标.
代数法:只能用判断交点的个数,不能判断两圆确切的位置关系,优点是可以求出交点的坐标.
位置关系 外离 外切 相交 内切 内含
圆与圆公共点个数 0 1 2 1 0
圆与圆方程联立(代数法)
d与R、r的关系(几何法) d>R+r d=R+r |R-r|什么是轨迹?
举例1
举例2
轨迹就是一个几何图形,是满足一定条件的点,常常把图形看成点的集合或点运动形成的轨迹. 所以求轨迹,就是求一个几何图形.求轨迹的方程就是求几何图形的方程。
课本例题
我们可以通过建立适当的平面直角坐标系,求得满足条件的动点M的轨迹方程,从而得到点M的轨迹;通过研究它的轨迹方程与圆O方程的关系,判断这个轨迹与圆O的位置关系。
课本例题
A
O
B
P
M
x
y
课本例题
思考探究
概念归纳
把几何问题求轨迹转化成代数问题求轨迹方程,再通过轨迹方程的代数特征回归到它是什么轨迹这个问题的结论中,这就是利用坐标法解决轨迹问题的基本步骤
坐标法求轨迹方程的步骤:建、设、限、代、化、检。
判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的个数问题.
相交弦及轨迹问题的解决
1.求两圆的公共弦所在直线的方程的方法:将两圆方程相减即得两圆公共弦所在直线方程,但必须注意只有当两圆方程中二次项系数相同时,才能如此求解,否则应先调整系数.
公共弦长度可以用交点得距离公式,也可以用勾股关系求解.
2.坐标法求轨迹问题:建、设、限、代、化、检.
概念归纳
当实数k为何值时,两圆C1:x2+y2+4x-6y+12=0,C2:x2+y2-2x-14y+k=0相交、相切、相离?
题型1 两圆位置关系的判定
典例剖析
1.几何法判断圆与圆的位置关系的步骤
(1)将两圆的方程化为标准方程;
(2)求两圆的圆心坐标和半径r1,r2;
(3)求两圆的圆心距d;
(4)比较d与|r1-r2|,r1+r2的大小关系,从而判断两圆的位置关系.
2.代数法判断圆与圆的位置关系的注意点
(1)由Δ=0得两圆相切,但无法区分内切或外切.
(2)由Δ<0得两圆相离,但无法区分内含或外离.
归纳总结
1.已知圆C1:x2+y2-2mx+4y+m2-5=0与圆C2:x2+y2+2x=0.
(1)当m=1时,判断圆C1与圆C2的位置关系;
(2)是否存在m使得圆C1与圆C2内含?
练一练
练一练
(多选)若圆C1:(x-1)2+y2=1与圆C2:x2+y2-8x+8y+m=0相切,则m的值可以是 ( )
A.16 B.7
C.-4 D.-7
题型2 与两圆相切有关的问题
典例剖析
探究一 已知两圆相切求变量范围
AC
典例剖析
题型2 与两圆相切有关的问题
探究二 两圆的公切线问题
B
BCD
已知直线l:y+2=0和圆C:x2+y2-2y=0,动圆M与l相切,且与C内切.当M的圆心距直线g:x-y-2=0最近时,求M的方程.
典例剖析
题型3 与两圆都相切的轨迹问题
处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须考虑分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
归纳总结
2.已知动圆M与y轴相切且与定圆A:(x-3)2+y2=9外切,则动圆的圆心M的轨迹方程是 ( )
A.y2=12x(x>0)
B.y=0(x<0)
C.y2=12x
D.y2=12x(x>0)或y=0(x<0)
练一练
D
练一练
3.已知以C(4,-3)为圆心的圆与圆O:x2+y2=1相切,则圆C的方程是______________.
【解析】若圆C与圆O外切,则rc+1=5,
所以rc=4.若圆C与圆O内切,
因为点C在圆O外,
所以rc-1=5,所以rc=6.
所以圆C的方程为
(x-4)2+(y+3)2=16或(x-4)2+(y+3)2=36.
(x-4)2+(y+3)2=16或(x-4)2+(y+3)2=36
练一练
已知⊙A的方程为x2+y2-2x-2y-7=0,⊙B的方程为x2+y2+2x+2y-2=0,判断⊙A和⊙B是否相交.若相交,求过两交点的直线的方程及两交点间的距离;若不相交,请说明理由.
典例剖析
题型4 与两圆相交有关的问题
归纳总结
1.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
2.两圆相交时,过交点的直线或圆的方程的求法
已知圆C1:x2+y2+D1x+E1y+F1=0,圆C2:x2+y2+D2x+E2y+F2=0,方程:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0,其中λ为任意实数.当两圆C1,C2相交时.
①若λ=-1,则方程表示过两圆C1,C2的交点的直线;
②若λ≠-1,则方程表示过两圆C1,C2的交点的圆系方程(但方程所表示的圆不包括圆C2,圆系中的一切圆都和C1,C2相交).
4.将本例中⊙A的方程改为x2+y2+2x-6y+1=0,⊙B的方程改为x2+y2-4x+2y-11=0,如何解答?
练一练
练一练
练一练
5.(拓展练)求经过点M(2,-2)以及圆x2+y2-6x=0与圆x2+y2=4交点的圆的方程.
解:设过圆x2+y2-6x=0与圆x2+y2=4交点的圆的方程为
x2+y2-6x+λ(x2+y2-4)=0①,
把点M(2,-2)代入①,得λ=1.
把λ=1代入①,化简得x2+y2-3x-2=0,
所以所求圆的方程为x2+y2-3x-2=0.
1.两圆x2+y2-1=0和x2+y2-4x+2y-4=0的位置关系是( )
A.内切 B.相交 C.外切 D.外离
2.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为( )
A.(x-4)2+(y-6)2=16 B.(x±4)2+(y-6)2=16
C.(x-4)2+(y-6)2=36 D.(x±4)2+(y-6)2=36
B
D
随堂练
随堂练
3.圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦所在的直线方程是 .
4.已知圆x2+y2=9与圆x2+y2+8x-6y+25-r2=0(r>0)有公共点,则r的取值范围是 .
4x+3y-2=0
[2,8]
课本练习
习题2.5
O
M
E
C
x
y
A
B
M
C
C1
解法二:相交圆系
B
A
C
O
x
y
B
A
C
O
x
y
解法二:相交圆系
C
A
B
M
O
x
y
N
C
F
E
11.如图,某台机器的三个轮齿,A和B啮合,C和B也啮合. 若A轮的直径为200 cm,B轮的直径为120 cm,C轮的直径为250 cm,且∠A=45°.试建立适当的坐标系,用坐标法求出A,C两齿轮的中心距离(精确到1 cm).
错因分析
易错辨析 忘记求相交两圆的公共弦方程的前提致错.
过两圆C1:x2+y2-2x-2y+1=0,C2:x2+y2-4x-21=0的交点所在的直线的方程为( )
A.x-y+11=0 B.x-y-11=0
C.x+y+11=0 D.不存在
D
错因分析
易错警示:忘记了两圆相交的前提,直接把两圆方程相减得x-y+11=0,错选A.
纠错心得:只有当两圆相交时,它的公共弦方程才是把两圆的方程对应相减得到;如果两圆不相交,则不能用这个结论.今后遇到类似问题,要先判断两圆的位置关系,再作决定
分层练习-基础
1.两圆x2+y2-1=0和x2+y2-4x+2y-4=0的位置关系是( )
A.内切 B.相交
C.外切 D.外离
2.圆C1:x2+y2-4x+2y+1=0与C2:x2+y2+4x-4y-1=0的公切线有( )
A.1条 B.2条
C.3条 D.4条
B
C
分层练习-基础
3.圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有( )
A.1条 B.2条
C.3条 D.4条
C
C
分层练习-基础
5.两圆x2+y2+2ax+2ay+2a2-3=0与x2+y2+2bx+2by+2b2-1=0公共弦长的最大值为________.
6.已知圆C1:x2+y2=4与圆C2:x2+y2-2ax+a2-1=0内切,则a等于________.
7.若曲线C1:x2+y2=5与曲线C2:x2+y2-2mx+m2-20=0(m∈R)相交于A,B两点,且两曲线在A处的切线互相垂直,则m的值是________.
8.已知圆C1:x2+y2-6x-7=0与圆C2:x2+y2-6y-27=0相交于A,B两点,则线段AB的中垂线方程为________.
2
±1
±5
x+y-3=0
分层练习-基础
分层练习-基础
分层练习-基础
10.已知过点M(0,2)且斜率为k的直线l与圆C:(x-1)2+y2=1交于A,B两点.
(1)求斜率k的取值范围;
(2)以点M为圆心,r为半径的圆与圆C总存在公共点,求r的取值范围;
(3)O为坐标原点,求证:直线OA与OB斜率之和为定值.
分层练习-基础
分层练习-基础
分层练习-巩固
C
分层练习-巩固
12.(多选)已知圆C1:x2+y2=r2,圆C2:(x-a)2+(y-b)2=r2(r>0)交于不同的A(x1,y1),B(x2,y2)两点,下列结论正确的有( )
A.a(x1-x2)+b(y1-y2)=0
B.2ax1+2by1=a2+b2
C.x1+x2=a
D.y1+y2=2b
ABC
分层练习-巩固
14.两圆x2+y2=16与(x-4)2+(y+3)2=r2(r>0)在交点处的切线互相垂直,则r=________.
13.若点A(a,b)在圆x2+y2=4上,则圆(x-a)2+y2=1与圆x2+(y-b)2=1的位置关系是________.
外切
3
分层练习-巩固
15.求以圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦为直径的圆C的方程.
分层练习-巩固
分层练习-巩固
16.如图,已知圆心坐标为M(,1)的圆M与x轴及直线y=x均相切,切点分别为A,B,另一圆N与x轴及直线y=x均相切,切点分别为C,D.圆M与圆N外切.
(1)求圆M和圆N的方程;
(2)过B点作MN的平行线l,求直线l被圆N截得的弦的长度.
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
人教版2019高一数学(选修一) 第二章 直线和圆的方程
2.5.2 直线的点斜式方程
学习目标
1.能根据给定圆的方程,用代数法判断圆与圆的位置关系
(重难点)
2.能根据给定圆的方程,用几何法判断圆与圆的位置关系
(重点)
3.两圆相交与相切问题(易错点)
情景导入
“打水漂”游戏别名轻功水上漂、七点漂、漂瓦.人们用扁形瓦片或石片,在手上呈水平放置后,用力飞出,石片擦水面飞行,石片碰水面后弹起再飞,石片不断在水面上向前弹跳,直至沉水.
在这一过程中,石片与水面接触形成了一个个逐渐扩大的圆,这些圆在变化的过程中位置关系是怎样的
1.圆与圆的位置关系
新知探究
我们知道,两个圆之间存在以下三种位置关系:
(1)两圆相交,有两个公共点;
(2)两圆相切,包括外切与内切,只有一个公共点;
(3)两圆相离,包括外离与内含,没有公共点.
类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?
O1
O2
两圆相交
O1
O2
O1
O2
两圆相切
O1
O2
O1
O2
两圆相离
内切
外切
外离
内含
两圆无公共点
两圆有一个公共点
两圆有两个公共点
问题2 类比直线与圆的位置关系几何法:
比较d与r之间的大小关系,你能归纳圆与圆的位置关系几何法的比较方式吗?
O1
O2
两圆相交
O1
O2
O1
O2
两圆相切
O1
O2
O1
O2
两圆相离
外离
内含
外切
内切
概念归纳
设圆C1的半径为r1,圆C2的半径为r2,圆心距|C1C2|=d,则
圆与圆位置关系的判定
课本例题
解法一: 把圆C1与圆C2的方程分别化成标准方程,得
∴圆C1与圆C2相交.
y
x
A
B
C2
C1
课本例题
解法二: 将圆C1与圆C2的方程联立,得到方程组
①-②,得
联立①③,消去y,可得
方程④的根的判别式△>0,所以方程④有两个
不相等的实数根x1= -1,x2= 3.
y
x
A
B
C2
C1
两圆有两个公共点,连接这两个公共点的线段叫公共弦,你能求它的方程吗?
代人方程③,得到y1= 1,y2= -1.因此圆C1与圆C2有两个公共点
A(-1,1),B(3, -1 ),这两个圆相交.
课本例题
解: 将圆C1与圆C2的方程联立,得到方程组
①-②,得
联立①③,消去y,可得
y
x
A
B
C2
C1
A(-1,1),B(3, -1 )
两圆有两个公共点,连接这两个公共点的线段叫公共弦,你能求出它的方程吗?
思考探究
y
x
A
B
C2
C1
A(-1,1),B(3, -1 )
消去y,可得
方法一:将圆C1与圆C2的方程联立,
方法二:将圆C1与圆C2的方程相减,得到
公共弦长的求法:
方法一:
将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
方法二:
求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
概念归纳
思考探究
思考探究
你能比较这两种方法的特征吗
几何法:直观,容易理解,可以判断两圆确切的位置关系,但不能求出交点坐标.
代数法:只能用判断交点的个数,不能判断两圆确切的位置关系,优点是可以求出交点的坐标.
位置关系 外离 外切 相交 内切 内含
圆与圆公共点个数 0 1 2 1 0
圆与圆方程联立(代数法)
d与R、r的关系(几何法) d>R+r d=R+r |R-r|
举例1
举例2
轨迹就是一个几何图形,是满足一定条件的点,常常把图形看成点的集合或点运动形成的轨迹. 所以求轨迹,就是求一个几何图形.求轨迹的方程就是求几何图形的方程。
课本例题
我们可以通过建立适当的平面直角坐标系,求得满足条件的动点M的轨迹方程,从而得到点M的轨迹;通过研究它的轨迹方程与圆O方程的关系,判断这个轨迹与圆O的位置关系。
课本例题
A
O
B
P
M
x
y
课本例题
思考探究
概念归纳
把几何问题求轨迹转化成代数问题求轨迹方程,再通过轨迹方程的代数特征回归到它是什么轨迹这个问题的结论中,这就是利用坐标法解决轨迹问题的基本步骤
坐标法求轨迹方程的步骤:建、设、限、代、化、检。
判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解的个数问题.
相交弦及轨迹问题的解决
1.求两圆的公共弦所在直线的方程的方法:将两圆方程相减即得两圆公共弦所在直线方程,但必须注意只有当两圆方程中二次项系数相同时,才能如此求解,否则应先调整系数.
公共弦长度可以用交点得距离公式,也可以用勾股关系求解.
2.坐标法求轨迹问题:建、设、限、代、化、检.
概念归纳
当实数k为何值时,两圆C1:x2+y2+4x-6y+12=0,C2:x2+y2-2x-14y+k=0相交、相切、相离?
题型1 两圆位置关系的判定
典例剖析
1.几何法判断圆与圆的位置关系的步骤
(1)将两圆的方程化为标准方程;
(2)求两圆的圆心坐标和半径r1,r2;
(3)求两圆的圆心距d;
(4)比较d与|r1-r2|,r1+r2的大小关系,从而判断两圆的位置关系.
2.代数法判断圆与圆的位置关系的注意点
(1)由Δ=0得两圆相切,但无法区分内切或外切.
(2)由Δ<0得两圆相离,但无法区分内含或外离.
归纳总结
1.已知圆C1:x2+y2-2mx+4y+m2-5=0与圆C2:x2+y2+2x=0.
(1)当m=1时,判断圆C1与圆C2的位置关系;
(2)是否存在m使得圆C1与圆C2内含?
练一练
练一练
(多选)若圆C1:(x-1)2+y2=1与圆C2:x2+y2-8x+8y+m=0相切,则m的值可以是 ( )
A.16 B.7
C.-4 D.-7
题型2 与两圆相切有关的问题
典例剖析
探究一 已知两圆相切求变量范围
AC
典例剖析
题型2 与两圆相切有关的问题
探究二 两圆的公切线问题
B
BCD
已知直线l:y+2=0和圆C:x2+y2-2y=0,动圆M与l相切,且与C内切.当M的圆心距直线g:x-y-2=0最近时,求M的方程.
典例剖析
题型3 与两圆都相切的轨迹问题
处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须考虑分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
归纳总结
2.已知动圆M与y轴相切且与定圆A:(x-3)2+y2=9外切,则动圆的圆心M的轨迹方程是 ( )
A.y2=12x(x>0)
B.y=0(x<0)
C.y2=12x
D.y2=12x(x>0)或y=0(x<0)
练一练
D
练一练
3.已知以C(4,-3)为圆心的圆与圆O:x2+y2=1相切,则圆C的方程是______________.
【解析】若圆C与圆O外切,则rc+1=5,
所以rc=4.若圆C与圆O内切,
因为点C在圆O外,
所以rc-1=5,所以rc=6.
所以圆C的方程为
(x-4)2+(y+3)2=16或(x-4)2+(y+3)2=36.
(x-4)2+(y+3)2=16或(x-4)2+(y+3)2=36
练一练
已知⊙A的方程为x2+y2-2x-2y-7=0,⊙B的方程为x2+y2+2x+2y-2=0,判断⊙A和⊙B是否相交.若相交,求过两交点的直线的方程及两交点间的距离;若不相交,请说明理由.
典例剖析
题型4 与两圆相交有关的问题
归纳总结
1.公共弦长的求法
(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.
(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
2.两圆相交时,过交点的直线或圆的方程的求法
已知圆C1:x2+y2+D1x+E1y+F1=0,圆C2:x2+y2+D2x+E2y+F2=0,方程:x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0,其中λ为任意实数.当两圆C1,C2相交时.
①若λ=-1,则方程表示过两圆C1,C2的交点的直线;
②若λ≠-1,则方程表示过两圆C1,C2的交点的圆系方程(但方程所表示的圆不包括圆C2,圆系中的一切圆都和C1,C2相交).
4.将本例中⊙A的方程改为x2+y2+2x-6y+1=0,⊙B的方程改为x2+y2-4x+2y-11=0,如何解答?
练一练
练一练
练一练
5.(拓展练)求经过点M(2,-2)以及圆x2+y2-6x=0与圆x2+y2=4交点的圆的方程.
解:设过圆x2+y2-6x=0与圆x2+y2=4交点的圆的方程为
x2+y2-6x+λ(x2+y2-4)=0①,
把点M(2,-2)代入①,得λ=1.
把λ=1代入①,化简得x2+y2-3x-2=0,
所以所求圆的方程为x2+y2-3x-2=0.
1.两圆x2+y2-1=0和x2+y2-4x+2y-4=0的位置关系是( )
A.内切 B.相交 C.外切 D.外离
2.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程为( )
A.(x-4)2+(y-6)2=16 B.(x±4)2+(y-6)2=16
C.(x-4)2+(y-6)2=36 D.(x±4)2+(y-6)2=36
B
D
随堂练
随堂练
3.圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦所在的直线方程是 .
4.已知圆x2+y2=9与圆x2+y2+8x-6y+25-r2=0(r>0)有公共点,则r的取值范围是 .
4x+3y-2=0
[2,8]
课本练习
习题2.5
O
M
E
C
x
y
A
B
M
C
C1
解法二:相交圆系
B
A
C
O
x
y
B
A
C
O
x
y
解法二:相交圆系
C
A
B
M
O
x
y
N
C
F
E
11.如图,某台机器的三个轮齿,A和B啮合,C和B也啮合. 若A轮的直径为200 cm,B轮的直径为120 cm,C轮的直径为250 cm,且∠A=45°.试建立适当的坐标系,用坐标法求出A,C两齿轮的中心距离(精确到1 cm).
错因分析
易错辨析 忘记求相交两圆的公共弦方程的前提致错.
过两圆C1:x2+y2-2x-2y+1=0,C2:x2+y2-4x-21=0的交点所在的直线的方程为( )
A.x-y+11=0 B.x-y-11=0
C.x+y+11=0 D.不存在
D
错因分析
易错警示:忘记了两圆相交的前提,直接把两圆方程相减得x-y+11=0,错选A.
纠错心得:只有当两圆相交时,它的公共弦方程才是把两圆的方程对应相减得到;如果两圆不相交,则不能用这个结论.今后遇到类似问题,要先判断两圆的位置关系,再作决定
分层练习-基础
1.两圆x2+y2-1=0和x2+y2-4x+2y-4=0的位置关系是( )
A.内切 B.相交
C.外切 D.外离
2.圆C1:x2+y2-4x+2y+1=0与C2:x2+y2+4x-4y-1=0的公切线有( )
A.1条 B.2条
C.3条 D.4条
B
C
分层练习-基础
3.圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有( )
A.1条 B.2条
C.3条 D.4条
C
C
分层练习-基础
5.两圆x2+y2+2ax+2ay+2a2-3=0与x2+y2+2bx+2by+2b2-1=0公共弦长的最大值为________.
6.已知圆C1:x2+y2=4与圆C2:x2+y2-2ax+a2-1=0内切,则a等于________.
7.若曲线C1:x2+y2=5与曲线C2:x2+y2-2mx+m2-20=0(m∈R)相交于A,B两点,且两曲线在A处的切线互相垂直,则m的值是________.
8.已知圆C1:x2+y2-6x-7=0与圆C2:x2+y2-6y-27=0相交于A,B两点,则线段AB的中垂线方程为________.
2
±1
±5
x+y-3=0
分层练习-基础
分层练习-基础
分层练习-基础
10.已知过点M(0,2)且斜率为k的直线l与圆C:(x-1)2+y2=1交于A,B两点.
(1)求斜率k的取值范围;
(2)以点M为圆心,r为半径的圆与圆C总存在公共点,求r的取值范围;
(3)O为坐标原点,求证:直线OA与OB斜率之和为定值.
分层练习-基础
分层练习-基础
分层练习-巩固
C
分层练习-巩固
12.(多选)已知圆C1:x2+y2=r2,圆C2:(x-a)2+(y-b)2=r2(r>0)交于不同的A(x1,y1),B(x2,y2)两点,下列结论正确的有( )
A.a(x1-x2)+b(y1-y2)=0
B.2ax1+2by1=a2+b2
C.x1+x2=a
D.y1+y2=2b
ABC
分层练习-巩固
14.两圆x2+y2=16与(x-4)2+(y+3)2=r2(r>0)在交点处的切线互相垂直,则r=________.
13.若点A(a,b)在圆x2+y2=4上,则圆(x-a)2+y2=1与圆x2+(y-b)2=1的位置关系是________.
外切
3
分层练习-巩固
15.求以圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦为直径的圆C的方程.
分层练习-巩固
分层练习-巩固
16.如图,已知圆心坐标为M(,1)的圆M与x轴及直线y=x均相切,切点分别为A,B,另一圆N与x轴及直线y=x均相切,切点分别为C,D.圆M与圆N外切.
(1)求圆M和圆N的方程;
(2)过B点作MN的平行线l,求直线l被圆N截得的弦的长度.
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
