人教A版高中数学选择性必修第一册3.2.1双曲线及其标准方程 课件(共34张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册3.2.1双曲线及其标准方程 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:52:44 | ||
图片预览








文档简介
(共34张PPT)
人教版2019高一数学(选修一) 第三章 圆锥曲线的方程
3.2.1双曲线及其标准方程
学习目标
1.理解双曲线的定义、几何图形和标准方程的推导过程.(重点)
2.掌握双曲线的标准方程及其求法.(重点)
3.会利用双曲线的定义和标准方程解决简单的问题.(难点)
1.椭圆的定义:
平面内与两个定点|F1F2|的距离的和等于常数(大于|F1F2| )的点的轨迹叫做椭圆.
2.椭圆的标准方程:
问题:如果把椭圆定义中“距离的和”改为“距离的差”那么动点的轨迹会发生怎样的变化?
复习导入
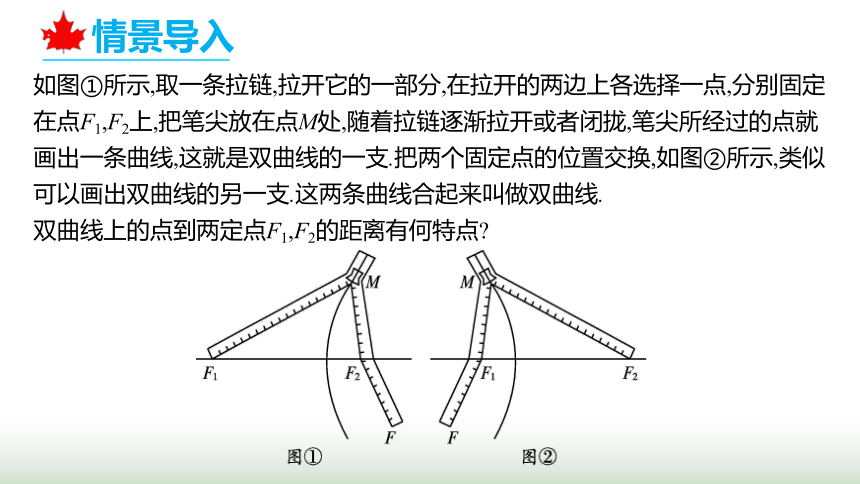
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,这就是双曲线的一支.把两个固定点的位置交换,如图②所示,类似可以画出双曲线的另一支.这两条曲线合起来叫做双曲线.
双曲线上的点到两定点F1,F2的距离有何特点
情景导入
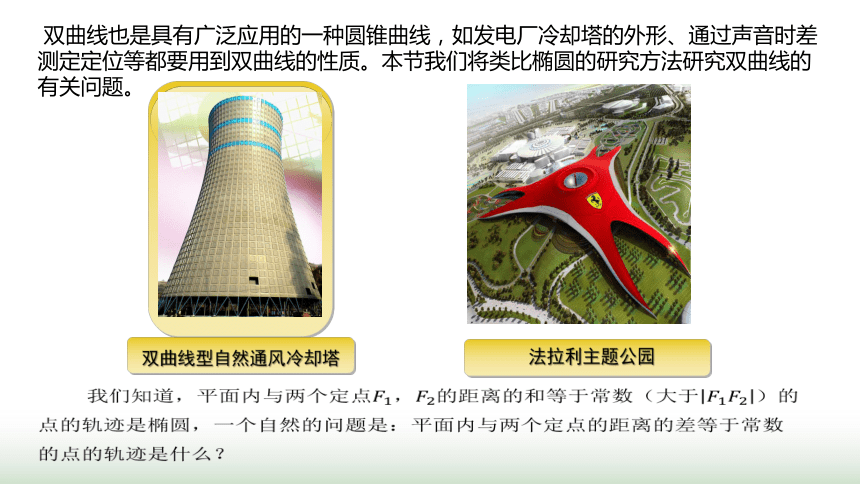
双曲线型自然通风冷却塔
法拉利主题公园
双曲线也是具有广泛应用的一种圆锥曲线,如发电厂冷却塔的外形、通过声音时差测定定位等都要用到双曲线的性质。本节我们将类比椭圆的研究方法研究双曲线的有关问题。
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
通常情况下,我们把|F1F2|记为2c(c>0), 常数记为2a(a>0),则双曲线定义还可以描述为
若||MF1|-|MF2||=2a<2c,则点M的轨迹是双曲线.
思考1 定义中为什么强调距离差的绝对值为常数?
一、双曲线的定义
如果不加绝对值,那得到的轨迹只是双曲线的一支.
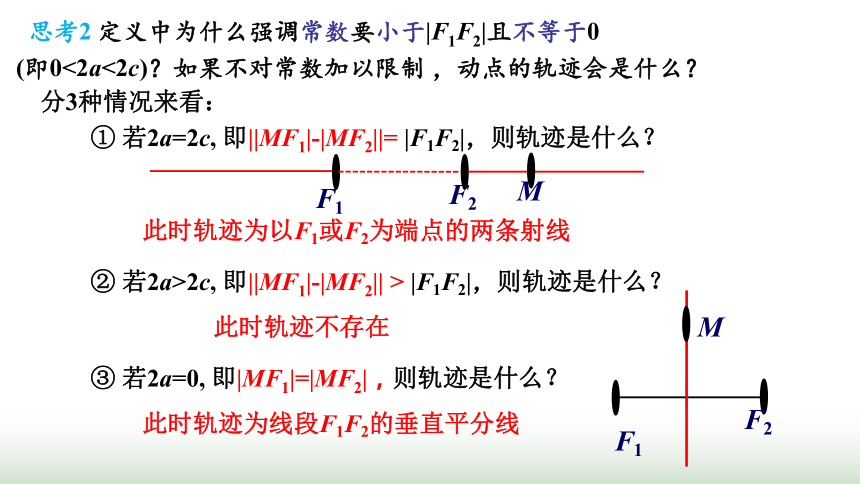
① 若2a=2c, 即||MF1|-|MF2||= |F1F2|,则轨迹是什么?
② 若2a>2c, 即||MF1|-|MF2|| > |F1F2|,则轨迹是什么?
③ 若2a=0, 即|MF1|=|MF2|,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
分3种情况来看:
思考2 定义中为什么强调常数要小于|F1F2|且不等于0
(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
F1
F2
M
F1
F2
M
设M(x,y)为双曲线上任一点, 双曲线的焦距为2c(c>0), 那么焦点F1,F2的坐标分别为 F1(-c,0), F2(c,0), 又设||MF1|-|MF2||=2a(0二、双曲线标准方程
① 建系:
如图示,建立平面直角坐标系.
② 设点:
③ 列式:
O
M
④ 化简整理得:
我们把上述方程叫做双曲线的标准方程,它表示焦点在x轴上,焦点坐标分别是F1(-c, 0), F2(c, 0)的双曲线,这里c2=a2+b2.
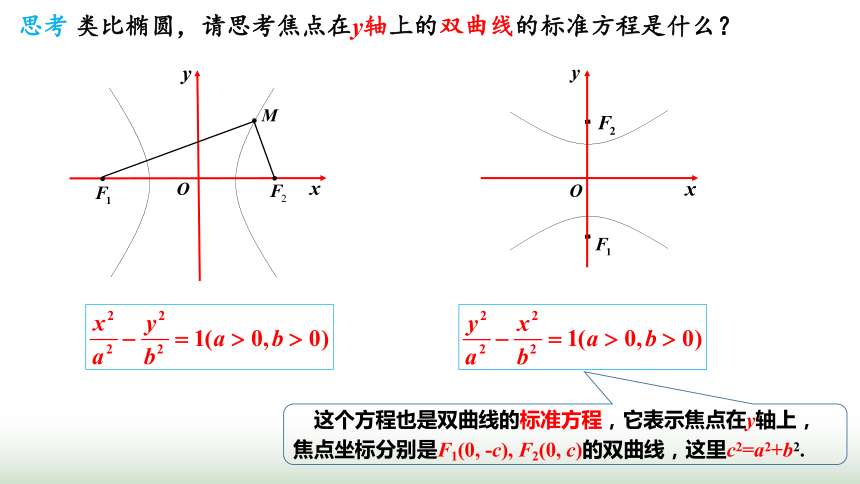
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
O
M
这个方程也是双曲线的标准方程,它表示焦点在y轴上,焦点坐标分别是F1(0, -c), F2(0, c)的双曲线,这里c2=a2+b2.
例1 已知双曲线的焦点 F1(-5, 0), F2(5, 0),双曲线上一点P到焦点的距离差的绝对值等于8,求双曲线的标准方程.
课本例题
例2 已知A, B两地相距800m, 在A地听到炮弹爆炸声比在B地晚2s, 且声速为340m/s, 求炮弹爆炸点的轨迹方程.
课本例题
想一想:如果A, B两处同时听到爆炸声,那么爆炸点应在什么样的曲线上?
答:爆炸点应在线段AB的中垂线上.
由例2可知,利用两个不同的观测点测得同一炮弹爆炸声的时间差 , 就可以确定爆炸点所在的双曲线的方程,但是不能确定爆炸点的准确位置.
要想确定爆炸点的准确位置,还需增设一个观测点C,利用A, C( 或B, C) 两处测得的爆炸声的时间差 , 求爆炸点所在的另一个双曲线的方程.
解这两个双曲线方程组成的方程组 , 就能确定爆炸点的准确位置 . 这是双曲线的一个重要应用 .
思考 如何准确测出爆炸点的位置?
x
y
o
B
A
P
C
A
B
M
O
x
y
探究 如图, 点A, B的坐标分别是(-5, 0), (5, 0), 直线AM, BM相交于点M,
且它们的斜率之积是 , 试求点M的轨迹方程, 并由点M的轨迹方程判
断轨迹的形式, 与3.1例3比较, 你有什么发现
解:
由方程可知,点M的轨迹是除去(-5,0),(5,0)两点且焦点在x轴上的双曲线.
1. 求适合下列条件的双曲线的标准方程.
(1) 焦点在轴x上,a=4,b=3 ;
(2) 焦点在轴x上,经过点
(3) 焦点为(0, -6), (0, 6), 且经过点(2, -5).
(2) ∵焦点在x轴上,故可设双曲线的标准方程为
课本练习
1. 求适合下列条件的双曲线的标准方程.
(1) 焦点在轴x上,a=4,b=3 ;
(2) 焦点在轴x上,经过点
(3) 焦点为(0, -6), (0, 6), 且经过点(2, -5).
(2)解2 : 设双曲线的方程为
1. 求适合下列条件的双曲线的标准方程.
(1) 焦点在轴x上,a=4,b=3 ;
(2) 焦点在轴x上,经过点
(3) 焦点为(0, -6), (0, 6), 且经过点(2, -5).
(3) 解1: ∵焦点在y轴上,故可设双曲线的标准方程为
证明:
解:
典例剖析
题型一:双曲线定义的应用
解 (1)设|MF1|=16,根据双曲线的定义知||MF2|-16|=6,即|MF2|-16=±6.
解得|MF2|=10或|MF2|=22.
归纳总结
题型二:求双曲线的标准方程
典例剖析
思路分析(1)结合a的值设出标准方程的两种形式,将点A的坐标代入求解.
(2)因为焦点相同,所以所求双曲线的焦点也在x轴上,且c2=16+4=20,利用待定系数法求解,或设出统一方程求解.
(3)双曲线焦点的位置不确定,可设出一般方程求解.
归纳总结
解 (1)由已知得,c=5,2a=8,即a=4.∵c2=a2+b2,∴b2=c2-a2=52-42=9.
∵焦点在x轴上,
(1)若该方程表示双曲线,求实数k的取值范围;
(2)若该方程表示焦点在y轴上的双曲线,求实数k的取值范围.
思路分析根据双曲线方程的特征建立不等式(组)求解.
题型三:双曲线标准方程的应用
典例剖析
归纳总结
【变式】(1)在方程mx2-my2=3n中,若mn<0,则该方程表示( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆 D.焦点在y轴上的双曲线
(2)若方程x2sin α-y2cos α=1(0≤α<π)表示双曲线,则α的取值范围是 .
课堂小结
人教版2019高一数学(选修一) 第三章 圆锥曲线的方程
3.2.1双曲线及其标准方程
学习目标
1.理解双曲线的定义、几何图形和标准方程的推导过程.(重点)
2.掌握双曲线的标准方程及其求法.(重点)
3.会利用双曲线的定义和标准方程解决简单的问题.(难点)
1.椭圆的定义:
平面内与两个定点|F1F2|的距离的和等于常数(大于|F1F2| )的点的轨迹叫做椭圆.
2.椭圆的标准方程:
问题:如果把椭圆定义中“距离的和”改为“距离的差”那么动点的轨迹会发生怎样的变化?
复习导入
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,这就是双曲线的一支.把两个固定点的位置交换,如图②所示,类似可以画出双曲线的另一支.这两条曲线合起来叫做双曲线.
双曲线上的点到两定点F1,F2的距离有何特点
情景导入
双曲线型自然通风冷却塔
法拉利主题公园
双曲线也是具有广泛应用的一种圆锥曲线,如发电厂冷却塔的外形、通过声音时差测定定位等都要用到双曲线的性质。本节我们将类比椭圆的研究方法研究双曲线的有关问题。
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
通常情况下,我们把|F1F2|记为2c(c>0), 常数记为2a(a>0),则双曲线定义还可以描述为
若||MF1|-|MF2||=2a<2c,则点M的轨迹是双曲线.
思考1 定义中为什么强调距离差的绝对值为常数?
一、双曲线的定义
如果不加绝对值,那得到的轨迹只是双曲线的一支.
① 若2a=2c, 即||MF1|-|MF2||= |F1F2|,则轨迹是什么?
② 若2a>2c, 即||MF1|-|MF2|| > |F1F2|,则轨迹是什么?
③ 若2a=0, 即|MF1|=|MF2|,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
分3种情况来看:
思考2 定义中为什么强调常数要小于|F1F2|且不等于0
(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
F1
F2
M
F1
F2
M
设M(x,y)为双曲线上任一点, 双曲线的焦距为2c(c>0), 那么焦点F1,F2的坐标分别为 F1(-c,0), F2(c,0), 又设||MF1|-|MF2||=2a(0
① 建系:
如图示,建立平面直角坐标系.
② 设点:
③ 列式:
O
M
④ 化简整理得:
我们把上述方程叫做双曲线的标准方程,它表示焦点在x轴上,焦点坐标分别是F1(-c, 0), F2(c, 0)的双曲线,这里c2=a2+b2.
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
O
M
这个方程也是双曲线的标准方程,它表示焦点在y轴上,焦点坐标分别是F1(0, -c), F2(0, c)的双曲线,这里c2=a2+b2.
例1 已知双曲线的焦点 F1(-5, 0), F2(5, 0),双曲线上一点P到焦点的距离差的绝对值等于8,求双曲线的标准方程.
课本例题
例2 已知A, B两地相距800m, 在A地听到炮弹爆炸声比在B地晚2s, 且声速为340m/s, 求炮弹爆炸点的轨迹方程.
课本例题
想一想:如果A, B两处同时听到爆炸声,那么爆炸点应在什么样的曲线上?
答:爆炸点应在线段AB的中垂线上.
由例2可知,利用两个不同的观测点测得同一炮弹爆炸声的时间差 , 就可以确定爆炸点所在的双曲线的方程,但是不能确定爆炸点的准确位置.
要想确定爆炸点的准确位置,还需增设一个观测点C,利用A, C( 或B, C) 两处测得的爆炸声的时间差 , 求爆炸点所在的另一个双曲线的方程.
解这两个双曲线方程组成的方程组 , 就能确定爆炸点的准确位置 . 这是双曲线的一个重要应用 .
思考 如何准确测出爆炸点的位置?
x
y
o
B
A
P
C
A
B
M
O
x
y
探究 如图, 点A, B的坐标分别是(-5, 0), (5, 0), 直线AM, BM相交于点M,
且它们的斜率之积是 , 试求点M的轨迹方程, 并由点M的轨迹方程判
断轨迹的形式, 与3.1例3比较, 你有什么发现
解:
由方程可知,点M的轨迹是除去(-5,0),(5,0)两点且焦点在x轴上的双曲线.
1. 求适合下列条件的双曲线的标准方程.
(1) 焦点在轴x上,a=4,b=3 ;
(2) 焦点在轴x上,经过点
(3) 焦点为(0, -6), (0, 6), 且经过点(2, -5).
(2) ∵焦点在x轴上,故可设双曲线的标准方程为
课本练习
1. 求适合下列条件的双曲线的标准方程.
(1) 焦点在轴x上,a=4,b=3 ;
(2) 焦点在轴x上,经过点
(3) 焦点为(0, -6), (0, 6), 且经过点(2, -5).
(2)解2 : 设双曲线的方程为
1. 求适合下列条件的双曲线的标准方程.
(1) 焦点在轴x上,a=4,b=3 ;
(2) 焦点在轴x上,经过点
(3) 焦点为(0, -6), (0, 6), 且经过点(2, -5).
(3) 解1: ∵焦点在y轴上,故可设双曲线的标准方程为
证明:
解:
典例剖析
题型一:双曲线定义的应用
解 (1)设|MF1|=16,根据双曲线的定义知||MF2|-16|=6,即|MF2|-16=±6.
解得|MF2|=10或|MF2|=22.
归纳总结
题型二:求双曲线的标准方程
典例剖析
思路分析(1)结合a的值设出标准方程的两种形式,将点A的坐标代入求解.
(2)因为焦点相同,所以所求双曲线的焦点也在x轴上,且c2=16+4=20,利用待定系数法求解,或设出统一方程求解.
(3)双曲线焦点的位置不确定,可设出一般方程求解.
归纳总结
解 (1)由已知得,c=5,2a=8,即a=4.∵c2=a2+b2,∴b2=c2-a2=52-42=9.
∵焦点在x轴上,
(1)若该方程表示双曲线,求实数k的取值范围;
(2)若该方程表示焦点在y轴上的双曲线,求实数k的取值范围.
思路分析根据双曲线方程的特征建立不等式(组)求解.
题型三:双曲线标准方程的应用
典例剖析
归纳总结
【变式】(1)在方程mx2-my2=3n中,若mn<0,则该方程表示( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆 D.焦点在y轴上的双曲线
(2)若方程x2sin α-y2cos α=1(0≤α<π)表示双曲线,则α的取值范围是 .
课堂小结
