人教A版高中数学选择性必修第一册3.3.1抛物线及其标准方程 课件(共23张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册3.3.1抛物线及其标准方程 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 10:53:24 | ||
图片预览







文档简介
(共23张PPT)
人教版2019高一数学(选修一) 第三章 圆锥曲线的方程
3.3.1 抛物线及其标准方程
1.掌握抛物线的定义及焦点、准线的概念.(重点)
2.掌握抛物线的标准方程及其推导过程.(易错点)
3.明确p的几何意义,并能解决简单的求抛物线标准方程问题.
(难点)
学习目标
我们把一根直尺固定在图板上直线l的位置,把一块三角尺的一条直角边紧靠着直尺的边缘,再把一条细绳的一端固定在三角尺的另一条直角边的一点A,取绳长等于点A到直角顶点C的长(即点A到直线l的距离),并且把绳子的另一端固定在图板上的一点F.用铅笔尖引着
绳子,使点A到笔尖的一段绳子紧靠着三角尺,然后将三角尺沿着直尺上下滑动,笔尖就在图板上描出了一条曲线.
这就是本节我们要学习的抛物线,这条曲线上的点有什么特征
情景导入
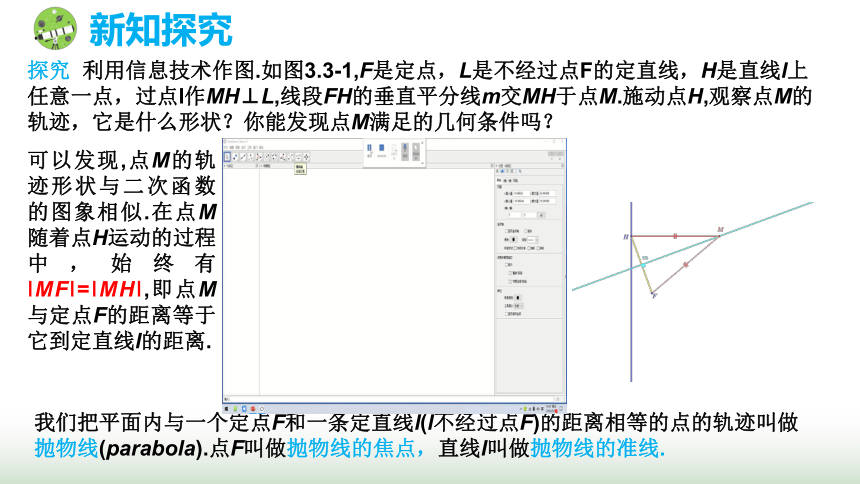
探究 利用信息技术作图.如图3.3-1,F是定点,L是不经过点F的定直线,H是直线l上任意一点,过点l作MH⊥L,线段FH的垂直平分线m交MH于点M.施动点H,观察点M的轨迹,它是什么形状?你能发现点M满足的几何条件吗?
可以发现,点M的轨迹形状与二次函数的图象相似.在点M随着点H运动的过程中,始终有 MF = MH ,即点M与定点F的距离等于它到定直线l的距离.
我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线(parabola).点F叫做抛物线的焦点,直线l叫做抛物线的准线.
新知探究
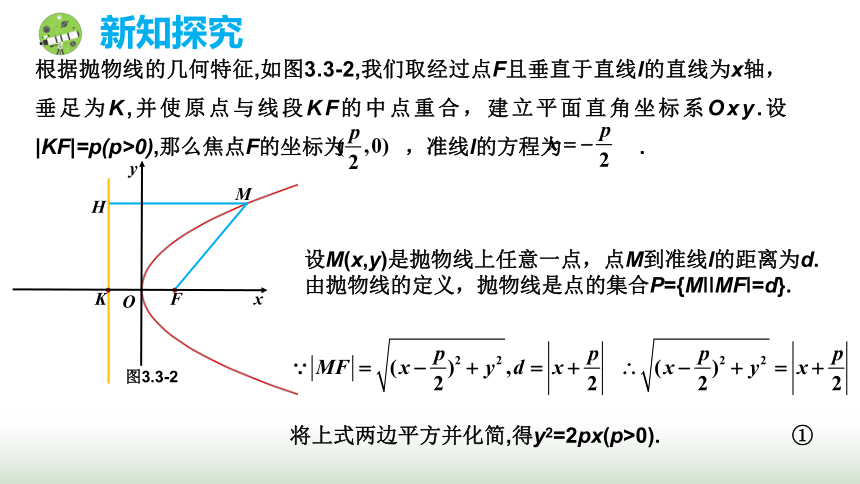
根据抛物线的几何特征,如图3.3-2,我们取经过点F且垂直于直线l的直线为x轴,垂足为K,并使原点与线段KF的中点重合,建立平面直角坐标系Oxy.设|KF|=p(p>0),那么焦点F的坐标为 ,准线l的方程为 .
K
F
M
x
y
O
图3.3-2
H
设M(x,y)是抛物线上任意一点,点M到准线l的距离为d.由抛物线的定义,抛物线是点的集合P={M MF =d}.
将上式两边平方并化简,得y2=2px(p>0). ①
新知探究
从上述过程可以看到,抛物线上任意一点的坐标(x,y)都是方程①的解,以方程①的解为坐标的点(x,y)与抛物线的焦点 的距离和它到准线 的距离相等,即以方程①的解为坐标的点都在抛物线上,我们把方程①叫做抛物线的标准方程,它表示焦点在x轴正半轴上,焦点是 ,准线是 的抛物线.
设M(x,y)是抛物线上任意一点,点M到准线l的距离为d.由抛物线的定义,抛物线是点的集合P={M MF =d}.
将上式两边平方并化简,得y2=2px(p>0). ①
K
F
M
x
y
O
H
在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同形式的标准方程,抛物线的标准方程有哪些不同的形式 请探究之后填写下表.
图像 标准方程 焦点坐标 准线方程
l
课本例题
l
课本练习
题型一:抛物线的标准方程
典例剖析
归纳总结
题型二:抛物线定义及应用
典例剖析
抛物线定义的两种应用
1.实现距离转化:根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,因此,由抛物线定义可以实现点点距离与点线距离的相互转化,从而简化某些问题.
2.解决最值问题:在抛物线中求解与焦点有关的两间间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.
归纳总结
题型三:抛物线的实际应用
典例剖析
求解抛物线实际应用题的5步骤
1.建系:建立适当的平面直角坐标系.
2.假设:设出合适的抛物线标准方程.
3.计算:通过计算求出抛物线的标准方程.
4.求解:求出所要求的量.
5.还原:还原到实际问题中,从而解决实际问题.
归纳总结
课堂小结
人教版2019高一数学(选修一) 第三章 圆锥曲线的方程
3.3.1 抛物线及其标准方程
1.掌握抛物线的定义及焦点、准线的概念.(重点)
2.掌握抛物线的标准方程及其推导过程.(易错点)
3.明确p的几何意义,并能解决简单的求抛物线标准方程问题.
(难点)
学习目标
我们把一根直尺固定在图板上直线l的位置,把一块三角尺的一条直角边紧靠着直尺的边缘,再把一条细绳的一端固定在三角尺的另一条直角边的一点A,取绳长等于点A到直角顶点C的长(即点A到直线l的距离),并且把绳子的另一端固定在图板上的一点F.用铅笔尖引着
绳子,使点A到笔尖的一段绳子紧靠着三角尺,然后将三角尺沿着直尺上下滑动,笔尖就在图板上描出了一条曲线.
这就是本节我们要学习的抛物线,这条曲线上的点有什么特征
情景导入
探究 利用信息技术作图.如图3.3-1,F是定点,L是不经过点F的定直线,H是直线l上任意一点,过点l作MH⊥L,线段FH的垂直平分线m交MH于点M.施动点H,观察点M的轨迹,它是什么形状?你能发现点M满足的几何条件吗?
可以发现,点M的轨迹形状与二次函数的图象相似.在点M随着点H运动的过程中,始终有 MF = MH ,即点M与定点F的距离等于它到定直线l的距离.
我们把平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线(parabola).点F叫做抛物线的焦点,直线l叫做抛物线的准线.
新知探究
根据抛物线的几何特征,如图3.3-2,我们取经过点F且垂直于直线l的直线为x轴,垂足为K,并使原点与线段KF的中点重合,建立平面直角坐标系Oxy.设|KF|=p(p>0),那么焦点F的坐标为 ,准线l的方程为 .
K
F
M
x
y
O
图3.3-2
H
设M(x,y)是抛物线上任意一点,点M到准线l的距离为d.由抛物线的定义,抛物线是点的集合P={M MF =d}.
将上式两边平方并化简,得y2=2px(p>0). ①
新知探究
从上述过程可以看到,抛物线上任意一点的坐标(x,y)都是方程①的解,以方程①的解为坐标的点(x,y)与抛物线的焦点 的距离和它到准线 的距离相等,即以方程①的解为坐标的点都在抛物线上,我们把方程①叫做抛物线的标准方程,它表示焦点在x轴正半轴上,焦点是 ,准线是 的抛物线.
设M(x,y)是抛物线上任意一点,点M到准线l的距离为d.由抛物线的定义,抛物线是点的集合P={M MF =d}.
将上式两边平方并化简,得y2=2px(p>0). ①
K
F
M
x
y
O
H
在建立椭圆、双曲线的标准方程时,选择不同的坐标系我们得到了不同形式的标准方程,抛物线的标准方程有哪些不同的形式 请探究之后填写下表.
图像 标准方程 焦点坐标 准线方程
l
课本例题
l
课本练习
题型一:抛物线的标准方程
典例剖析
归纳总结
题型二:抛物线定义及应用
典例剖析
抛物线定义的两种应用
1.实现距离转化:根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,因此,由抛物线定义可以实现点点距离与点线距离的相互转化,从而简化某些问题.
2.解决最值问题:在抛物线中求解与焦点有关的两间间距离和的最小值时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.
归纳总结
题型三:抛物线的实际应用
典例剖析
求解抛物线实际应用题的5步骤
1.建系:建立适当的平面直角坐标系.
2.假设:设出合适的抛物线标准方程.
3.计算:通过计算求出抛物线的标准方程.
4.求解:求出所要求的量.
5.还原:还原到实际问题中,从而解决实际问题.
归纳总结
课堂小结
