苏教版六年级下册数学立体图形的表面积和体积整理与复习课件(共23张PPT)
文档属性
| 名称 | 苏教版六年级下册数学立体图形的表面积和体积整理与复习课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 00:00:00 | ||
图片预览

文档简介
(共23张PPT)
立体图形的表面积和体积
苏教版 六年级下册 总复习
回忆一下,我们学过的立体图形有哪些?
在小组里说一说,你用什么方式整理了哪些内容?
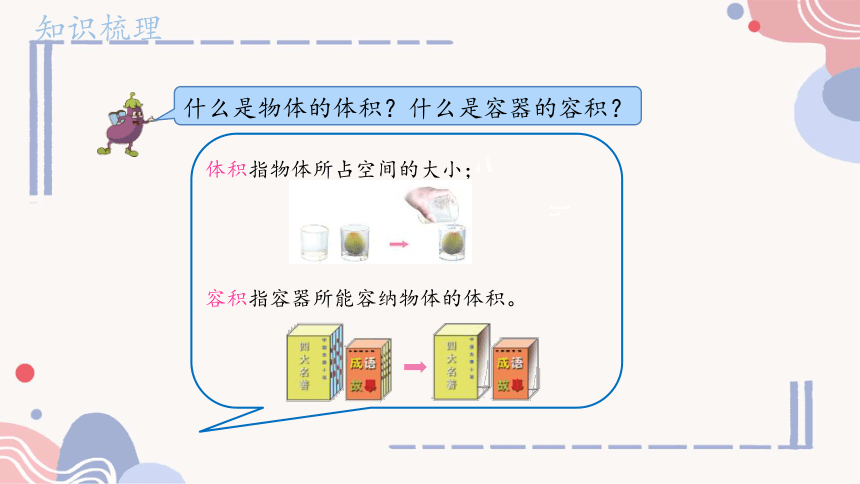
什么是物体的体积?什么是容器的容积?
体积指物体所占空间的大小;
容积指容器所能容纳物体的体积。
知识梳理
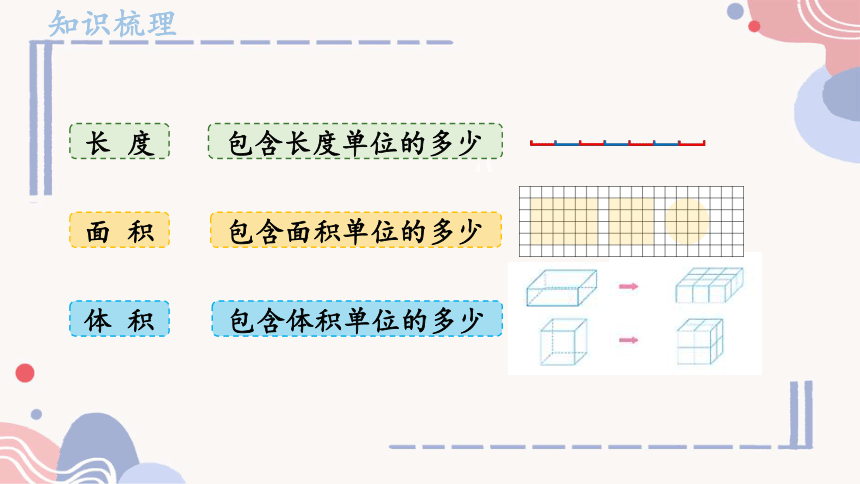
长 度
面 积
体 积
包含长度单位的多少
包含体积单位的多少
包含面积单位的多少
知识梳理
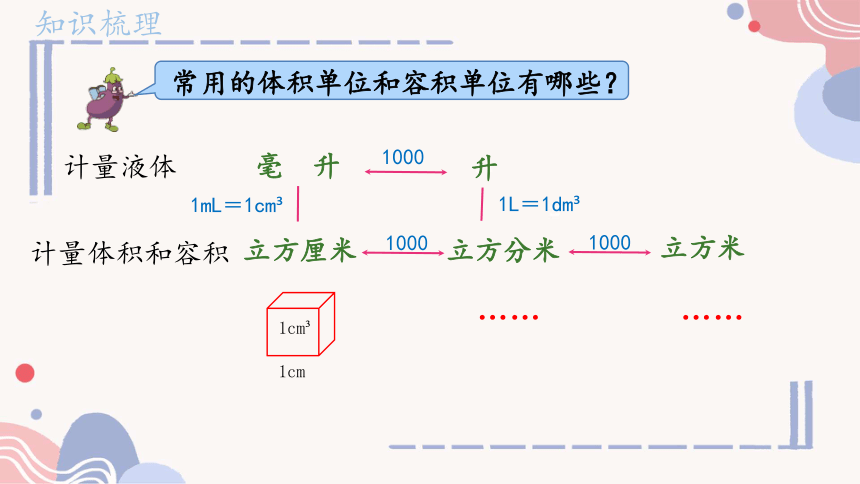
常用的体积单位和容积单位有哪些?
立方厘米
立方分米
立方米
1000
毫 升
升
计量体积和容积
计量液体
1cm
……
……
1000
1mL=1cm
1L=1dm
1000
知识梳理
1cm
× ×
× ×
整理与反思
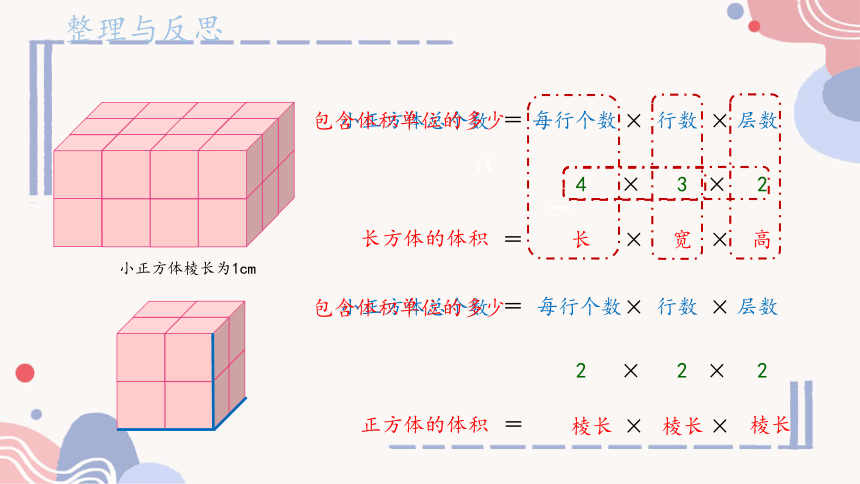
小正方体棱长为1cm
每行个数
行数
层数
4
3
2
小正方体总个数
长
宽
高
× ×
长方体的体积
=
包含体积单位的多少
=
× ×
× ×
行数
层数
2
2
2
小正方体总个数
× ×
棱长
棱长
棱长
正方体的体积
=
=
每行个数
包含体积单位的多少
整理与反思
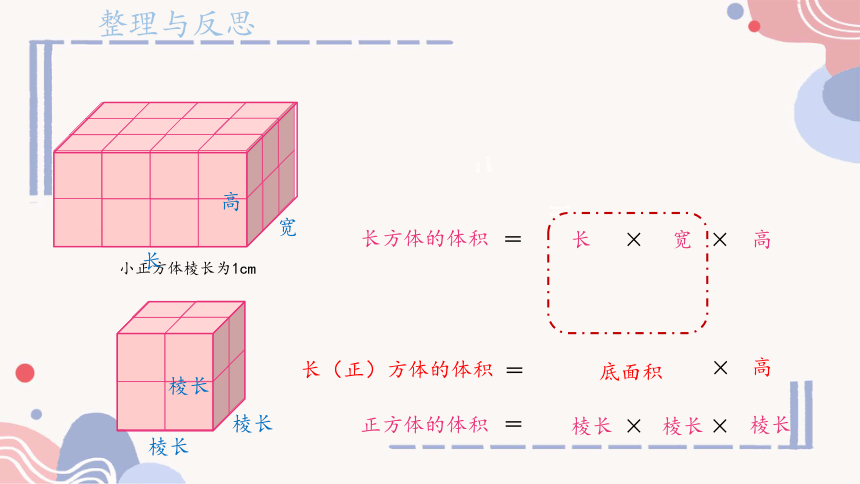
小正方体棱长为1cm
× ×
长
宽
高
长方体的体积
=
× ×
棱长
棱长
棱长
正方体的体积
=
高
×
长(正)方体的体积
=
底面积
长
宽
高
棱长
棱长
棱长
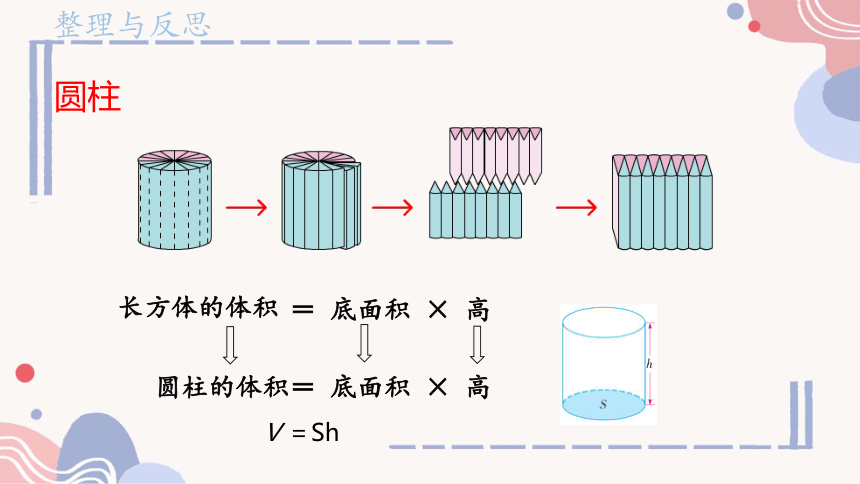
圆柱的体积= 底面积 × 高
V =Sh
圆柱
长方体的体积
= 底面积 × 高
整理与反思
整理与反思
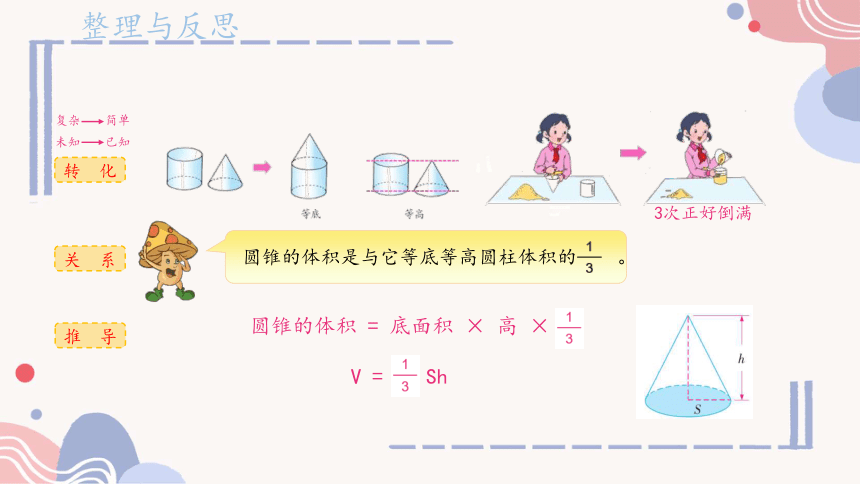
3次正好倒满
圆锥的体积 = 底面积 × 高 ×
圆锥的体积是与它等底等高圆柱体积的 。
V = Sh
转 化
关 系
推 导
未知 已知
复杂 简单
整理与反思
这些体积计算公式之间有什么内在联系?
V = Sh
V=πr h
=Sh
V=abh
=Sh
V=a
=Sh
什么是长方体、正方体和圆柱的表面积?
知识梳理
知识梳理
长方体的表面积=(长×宽+长×高+宽×高)×2
长方体
正方体
正方体的表面积=棱长×棱长×6
立体图形的表面积
圆柱
圆柱的表面积 =侧面积+2个底面积
底面周长×高
知识梳理
如果给你一张A4纸(长方形纸),不允许剪裁,可以创造出哪些立体图形?这张纸与立体图形之间又有什么联系呢?先自己动手试一试,等会儿请你来做展示哦!
实践与拓展
立体图形的侧面积=底面周长×高
观察这些立体图形的展开图,你有什么发现?
立体图形的表面积=侧面积+底面积×2
实践与拓展
立体图形(直柱体)的体积=底面积×高
想一想:除了卷一卷、折一折,还有别的方法得到这些立体图形吗?
练习与实践
制作这样一个油桶,至少需要多少铁皮?
表面积
侧面积+底面积×2
有关表面积的问题,还可能求……
游泳池
侧面积+底面积
侧面积
压路机压路的面积
一周商标纸
练习与实践
一个长方体,表面积是184平方分米,一个底面积是32平方分米,底面周长是24分米,求这个长方体的体积。
184-32×2=120(平方分米)
120÷24=5(分米)
32×5=160(立方分米)
答:这个长方体的体积是160立方分米。
练习与实践
求下面立体图形的体积。
(1)一个正方体,底面周长是 8 dm。
(2)一个长方体,底面是边长12cm 的正方形,高是50cm。
8÷4=2(分米)
2×2×2=8(立方分米)
答:正方体的体积是8立方分米。
12×12×50 = 7200(立方厘米)
答:长方体的体积是7200立方厘米。
底面积
高
底面积
高
练习与实践
(3)一个圆柱,底面周长是 12.56 cm,高是 5 cm。
(4)一个圆锥,底面半径是 3 cm,高是 4.5 cm。
12.56÷3.14÷2 =2(厘米)
22 π×5=20π(立方厘米)
答:圆柱的体积是20π立方厘米。
32 π×4.5×
=9π×4.5×
=13.5π(立方厘米)答:圆锥的体积是13.5π立方厘米。
底面积
高
底面积
高
练习与实践
联 系
统 一
灵 活
立体图形的表面积和体积
苏教版 六年级下册 总复习
回忆一下,我们学过的立体图形有哪些?
在小组里说一说,你用什么方式整理了哪些内容?
什么是物体的体积?什么是容器的容积?
体积指物体所占空间的大小;
容积指容器所能容纳物体的体积。
知识梳理
长 度
面 积
体 积
包含长度单位的多少
包含体积单位的多少
包含面积单位的多少
知识梳理
常用的体积单位和容积单位有哪些?
立方厘米
立方分米
立方米
1000
毫 升
升
计量体积和容积
计量液体
1cm
……
……
1000
1mL=1cm
1L=1dm
1000
知识梳理
1cm
× ×
× ×
整理与反思
小正方体棱长为1cm
每行个数
行数
层数
4
3
2
小正方体总个数
长
宽
高
× ×
长方体的体积
=
包含体积单位的多少
=
× ×
× ×
行数
层数
2
2
2
小正方体总个数
× ×
棱长
棱长
棱长
正方体的体积
=
=
每行个数
包含体积单位的多少
整理与反思
小正方体棱长为1cm
× ×
长
宽
高
长方体的体积
=
× ×
棱长
棱长
棱长
正方体的体积
=
高
×
长(正)方体的体积
=
底面积
长
宽
高
棱长
棱长
棱长
圆柱的体积= 底面积 × 高
V =Sh
圆柱
长方体的体积
= 底面积 × 高
整理与反思
整理与反思
3次正好倒满
圆锥的体积 = 底面积 × 高 ×
圆锥的体积是与它等底等高圆柱体积的 。
V = Sh
转 化
关 系
推 导
未知 已知
复杂 简单
整理与反思
这些体积计算公式之间有什么内在联系?
V = Sh
V=πr h
=Sh
V=abh
=Sh
V=a
=Sh
什么是长方体、正方体和圆柱的表面积?
知识梳理
知识梳理
长方体的表面积=(长×宽+长×高+宽×高)×2
长方体
正方体
正方体的表面积=棱长×棱长×6
立体图形的表面积
圆柱
圆柱的表面积 =侧面积+2个底面积
底面周长×高
知识梳理
如果给你一张A4纸(长方形纸),不允许剪裁,可以创造出哪些立体图形?这张纸与立体图形之间又有什么联系呢?先自己动手试一试,等会儿请你来做展示哦!
实践与拓展
立体图形的侧面积=底面周长×高
观察这些立体图形的展开图,你有什么发现?
立体图形的表面积=侧面积+底面积×2
实践与拓展
立体图形(直柱体)的体积=底面积×高
想一想:除了卷一卷、折一折,还有别的方法得到这些立体图形吗?
练习与实践
制作这样一个油桶,至少需要多少铁皮?
表面积
侧面积+底面积×2
有关表面积的问题,还可能求……
游泳池
侧面积+底面积
侧面积
压路机压路的面积
一周商标纸
练习与实践
一个长方体,表面积是184平方分米,一个底面积是32平方分米,底面周长是24分米,求这个长方体的体积。
184-32×2=120(平方分米)
120÷24=5(分米)
32×5=160(立方分米)
答:这个长方体的体积是160立方分米。
练习与实践
求下面立体图形的体积。
(1)一个正方体,底面周长是 8 dm。
(2)一个长方体,底面是边长12cm 的正方形,高是50cm。
8÷4=2(分米)
2×2×2=8(立方分米)
答:正方体的体积是8立方分米。
12×12×50 = 7200(立方厘米)
答:长方体的体积是7200立方厘米。
底面积
高
底面积
高
练习与实践
(3)一个圆柱,底面周长是 12.56 cm,高是 5 cm。
(4)一个圆锥,底面半径是 3 cm,高是 4.5 cm。
12.56÷3.14÷2 =2(厘米)
22 π×5=20π(立方厘米)
答:圆柱的体积是20π立方厘米。
32 π×4.5×
=9π×4.5×
=13.5π(立方厘米)答:圆锥的体积是13.5π立方厘米。
底面积
高
底面积
高
练习与实践
联 系
统 一
灵 活
