山西省山西大学附属中学校2024-2025学年高一下学期期中考试数学试题(图片版,含详解)
文档属性
| 名称 | 山西省山西大学附属中学校2024-2025学年高一下学期期中考试数学试题(图片版,含详解) |  | |
| 格式 | |||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 09:39:38 | ||
图片预览



文档简介
山西省山西大学附属中学校 2024-2025 学年高一下
学期期中考试数学试题
一、单选题
1. 若复数 满足 ,则 的虚部为( )
A. B. C. D.
2. 如图,已知 为平行四边形 内一点, ,则 等
于( )
A. B. C. D.
3. 如图所示,在三棱台 中,截去三棱锥 ,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.组合体
4. 已知平面向量 , ,则 在 上的投影向量为( )
A. B. C. D.
5. 在△ABC中,角 A,B,C对边分别为 a,b,c, ,且
,则 ( )
A. B. C. D.
6. 在 中, , 是 的中点, 与 交于点 ,若
,则 ( )
A. B. C. D.1
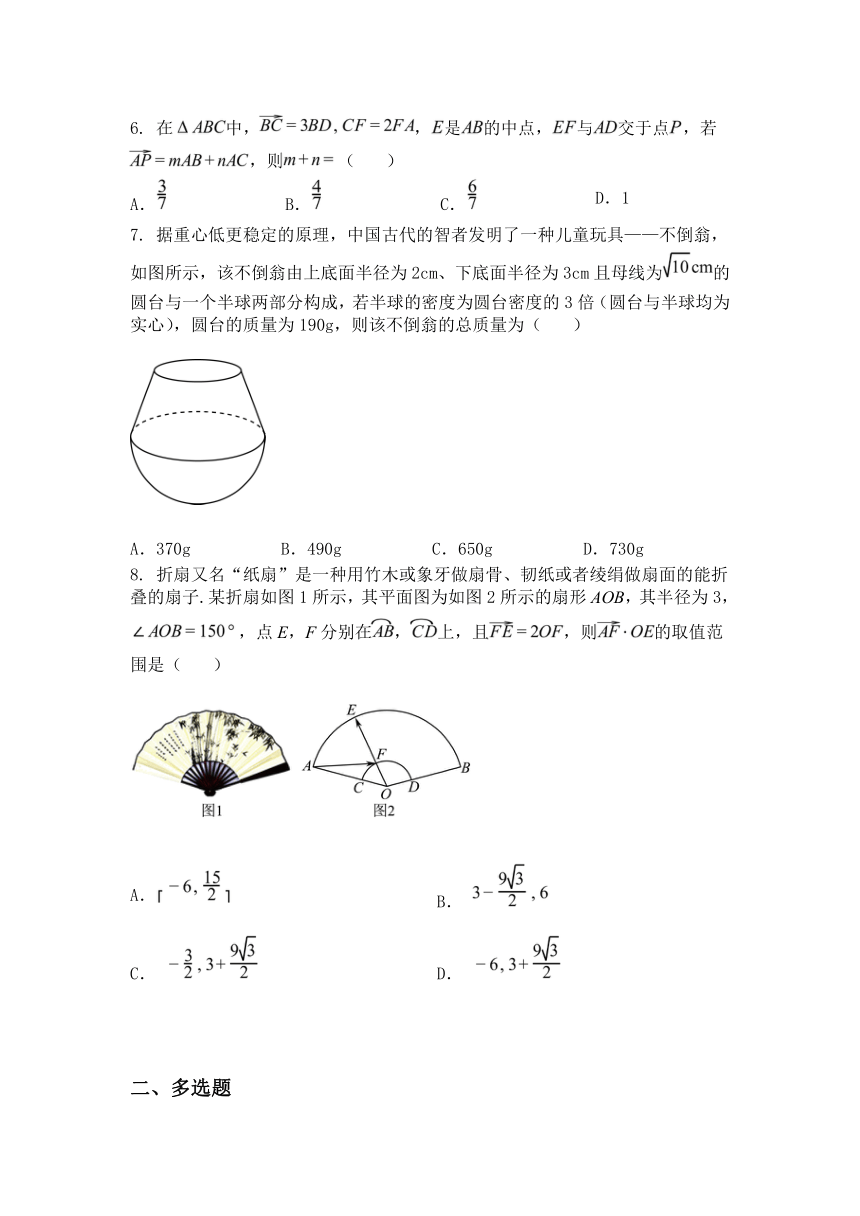
7. 据重心低更稳定的原理,中国古代的智者发明了一种儿童玩具——不倒翁,
如图所示,该不倒翁由上底面半径为 2cm、下底面半径为 3cm 且母线为 的
圆台与一个半球两部分构成,若半球的密度为圆台密度的 3倍(圆台与半球均为
实心),圆台的质量为 190g,则该不倒翁的总质量为( )
A.370g B.490g C.650g D.730g
8. 折扇又名“纸扇”是一种用竹木或象牙做扇骨、韧纸或者绫绢做扇面的能折
叠的扇子.某折扇如图 1所示,其平面图为如图 2所示的扇形 AOB,其半径为 3,
,点 E,F分别在 , 上,且 ,则 的取值范
围是( )
A. B.
C. D.
二、多选题
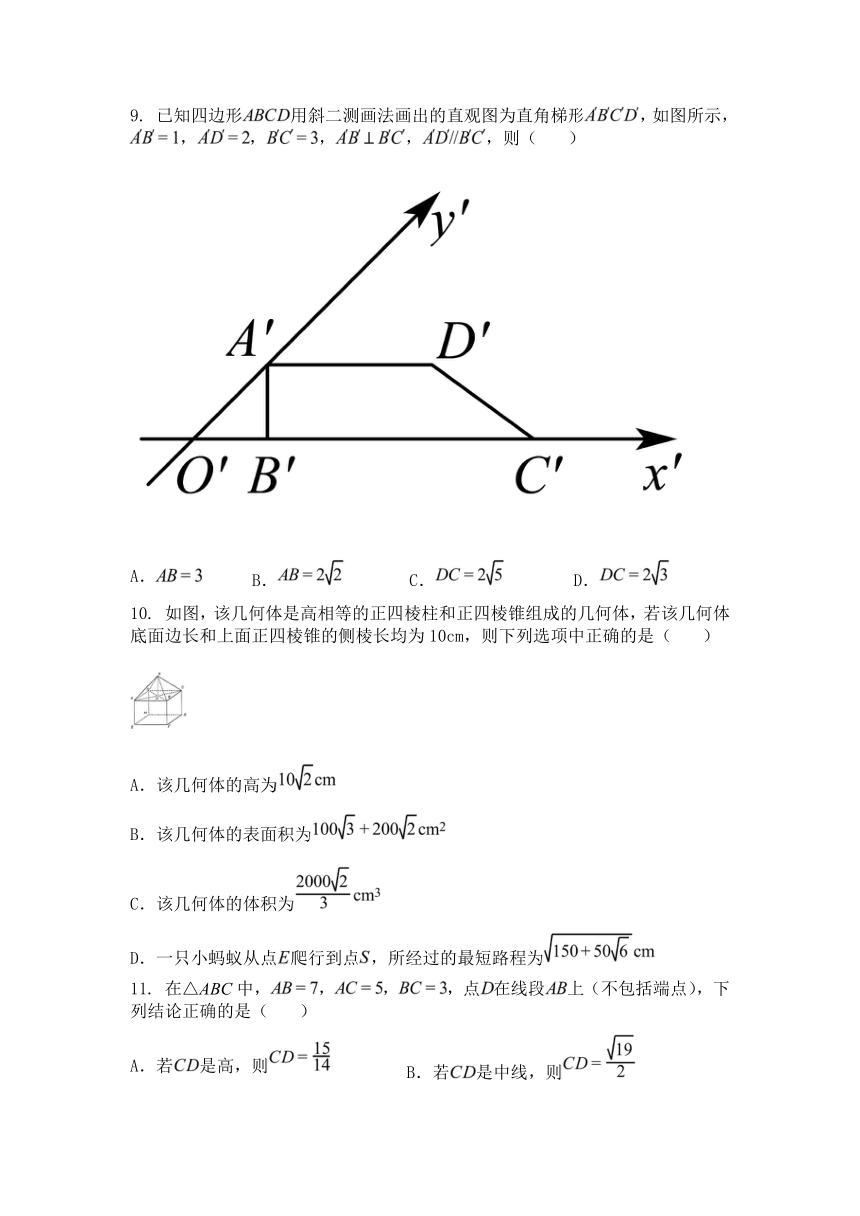
9. 已知四边形 用斜二测画法画出的直观图为直角梯形 ,如图所示,
, , , , ,则( )
A. B. C. D.
10. 如图,该几何体是高相等的正四棱柱和正四棱锥组成的几何体,若该几何体
底面边长和上面正四棱锥的侧棱长均为 10cm,则下列选项中正确的是( )
A.该几何体的高为
B.该几何体的表面积为
C.该几何体的体积为
D.一只小蚂蚁从点 爬行到点 ,所经过的最短路程为
11. 在△ABC中, , , ,点 在线段 上(不包括端点),下
列结论正确的是( )
A.若 是高,则 B.若 是中线,则
C.若 是角平分线,则 D.若 ,则 是线段 的三等分点
三、填空题
12. 复数 z满足 ,则复数 z的模的最大值是______.
13. 已知球 的表面积为 ,平面 截球 所得的截面面积为 ,则以 为顶点,
截面为底面的圆锥的体积为__________.
14. 目前,中国已经建成全球最大的 5G 网络,无论是大山深处还是广袤平原,
处处都能见到 5G 基站的身影.如图,某同学在一条水平公路上观测对面山顶上的
一座 5G 基站 ,已知基站高 m,该同学眼高 1.5m(眼睛到地面的距离),
该同学在初始位置 C处(眼睛所在位置)测得基站底部 B的仰角为 37°,测得
基站顶端 A的仰角为 45°.求出山高 ______m(用参考数据进行计算);
如图,当该同学面向基站 AB前行时(保持在同一铅垂面内),记该同学所在位
置 C处(眼睛所在位置)到基站 所在直线的距离 m,且记在 C处观测
基站底部 B的仰角为α,观测基站顶端 A的仰角为β.试问当 _____m时,观测
基站的视角 最大?参考数据: , , ,
, .
四、解答题
15. 设 , ,向量 , , ,且 , .
(1)求 ;
(2)求向量 与 夹角的余弦值.
16. (1)计算: ;
(2)已知 是虚数单位, 表示 的共轭复数,复数 满足 ,求 的
值.
17. 如图,三棱柱 的侧棱垂直于底面,其高为 2cm,底面三角形的
边长分别为 3cm,4cm,5cm.
(1)以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积 ;
(2)求该三棱柱的外接球的表面积.
18. 在面积为 S的 中,内角 A,B,C所对的边分别为 a,b,c,且
.
(1)若 ,试判断 的形状,并说明理由;
(2)若 ,则 的面积为 ,求 , 的值;
(3)若 为锐角三角形,求 的取值范围.
19. “费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:
在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.意大利
数学家托里拆利给出了解答,当 的三个内角均小于 时,使得
的点 即为费马点;当 有一个内角大于
或等于 时,最大内角的顶点为费马点.试用以上知识解决下面的问题:
(1)若 是边长为的 6等边三角形,求该三角形的费马点 到各顶点的距离
之和;
(2) 的内角 , , 所对的边分别为 , , ,且 ,点 为 的
费马点.
(i)若 ,求 ;
(ii)求 的最小值.
山西省山西大学附属中学校 2024-2025 学年高一下学期期中考试数学试题
整体难度:适中
考试范围:复数、平面向量、空间向量与立体几何、三角函数与解三角形、等式与不等式
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 2
较易 7
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 求复数的实部与虚部;复数代数形式的乘法运算
2 0.65 向量加法法则的几何应用;向量减法法则的几何应用
3 0.94 棱锥的结构特征和分类;棱台的结构特征和分类
4 0.85 数量积的坐标表示;求投影向量
5 0.65 余弦定理解三角形;已知模求数量积
向量的线性运算的几何应用;平面向量基本定理的应用;平面向量共线定理的推
6 0.4
论
7 0.85 台体体积的有关计算;球的体积的有关计算;求组合体的体积
8 0.65 求 cosx(型)函数的值域;数量积的运算律;向量加法法则的几何应用
二、多选题
9 0.85 斜二测画法中有关量的计算;由直观图还原几何图形
棱柱的展开图及最短距离问题;正棱锥及其有关计算;求组合多面体的表面积;
10 0.65
求组合体的体积
11 0.65 余弦定理解三角形;用向量解决线段的长度问题
三、填空题
12 0.85 与复数模相关的轨迹(图形)问题
13 0.85 球的截面的性质及计算;锥体体积的有关计算;球的表面积的有关计算
用和、差角的正切公式化简、求值;正弦定理解三角形;高度测量问题;基本不
14 0.65
等式求和的最小值
四、解答题
向量夹角的计算;向量垂直的坐标表示;由向量共线(平行)求参数;坐标计算
15 0.65
向量的模
复数代数形式的乘法运算;复数的除法运算;求复数的模;共轭复数的概念及计
16 0.85
算
多面体与球体内切外接问题;求组合体的体积;柱体体积的有关计算;球的表面
17 0.65
积的有关计算
三角形面积公式及其应用;正弦定理边角互化的应用;余弦定理解三角形;正、
18 0.85
余弦定理判定三角形形状
三角形面积公式及其应用;余弦定理解三角形;用定义求向量的数量积;基本不
19 0.65
等式求和的最小值
知识点分析
序号 知识点 对应题号
1 复数 1,12,16
2 平面向量 2,4,5,6,8,11,15,19
3 空间向量与立体几何 3,7,9,10,13,17
4 三角函数与解三角形 5,8,11,14,18,19
5 等式与不等式 14,19
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
学期期中考试数学试题
一、单选题
1. 若复数 满足 ,则 的虚部为( )
A. B. C. D.
2. 如图,已知 为平行四边形 内一点, ,则 等
于( )
A. B. C. D.
3. 如图所示,在三棱台 中,截去三棱锥 ,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.组合体
4. 已知平面向量 , ,则 在 上的投影向量为( )
A. B. C. D.
5. 在△ABC中,角 A,B,C对边分别为 a,b,c, ,且
,则 ( )
A. B. C. D.
6. 在 中, , 是 的中点, 与 交于点 ,若
,则 ( )
A. B. C. D.1
7. 据重心低更稳定的原理,中国古代的智者发明了一种儿童玩具——不倒翁,
如图所示,该不倒翁由上底面半径为 2cm、下底面半径为 3cm 且母线为 的
圆台与一个半球两部分构成,若半球的密度为圆台密度的 3倍(圆台与半球均为
实心),圆台的质量为 190g,则该不倒翁的总质量为( )
A.370g B.490g C.650g D.730g
8. 折扇又名“纸扇”是一种用竹木或象牙做扇骨、韧纸或者绫绢做扇面的能折
叠的扇子.某折扇如图 1所示,其平面图为如图 2所示的扇形 AOB,其半径为 3,
,点 E,F分别在 , 上,且 ,则 的取值范
围是( )
A. B.
C. D.
二、多选题
9. 已知四边形 用斜二测画法画出的直观图为直角梯形 ,如图所示,
, , , , ,则( )
A. B. C. D.
10. 如图,该几何体是高相等的正四棱柱和正四棱锥组成的几何体,若该几何体
底面边长和上面正四棱锥的侧棱长均为 10cm,则下列选项中正确的是( )
A.该几何体的高为
B.该几何体的表面积为
C.该几何体的体积为
D.一只小蚂蚁从点 爬行到点 ,所经过的最短路程为
11. 在△ABC中, , , ,点 在线段 上(不包括端点),下
列结论正确的是( )
A.若 是高,则 B.若 是中线,则
C.若 是角平分线,则 D.若 ,则 是线段 的三等分点
三、填空题
12. 复数 z满足 ,则复数 z的模的最大值是______.
13. 已知球 的表面积为 ,平面 截球 所得的截面面积为 ,则以 为顶点,
截面为底面的圆锥的体积为__________.
14. 目前,中国已经建成全球最大的 5G 网络,无论是大山深处还是广袤平原,
处处都能见到 5G 基站的身影.如图,某同学在一条水平公路上观测对面山顶上的
一座 5G 基站 ,已知基站高 m,该同学眼高 1.5m(眼睛到地面的距离),
该同学在初始位置 C处(眼睛所在位置)测得基站底部 B的仰角为 37°,测得
基站顶端 A的仰角为 45°.求出山高 ______m(用参考数据进行计算);
如图,当该同学面向基站 AB前行时(保持在同一铅垂面内),记该同学所在位
置 C处(眼睛所在位置)到基站 所在直线的距离 m,且记在 C处观测
基站底部 B的仰角为α,观测基站顶端 A的仰角为β.试问当 _____m时,观测
基站的视角 最大?参考数据: , , ,
, .
四、解答题
15. 设 , ,向量 , , ,且 , .
(1)求 ;
(2)求向量 与 夹角的余弦值.
16. (1)计算: ;
(2)已知 是虚数单位, 表示 的共轭复数,复数 满足 ,求 的
值.
17. 如图,三棱柱 的侧棱垂直于底面,其高为 2cm,底面三角形的
边长分别为 3cm,4cm,5cm.
(1)以上、下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积 ;
(2)求该三棱柱的外接球的表面积.
18. 在面积为 S的 中,内角 A,B,C所对的边分别为 a,b,c,且
.
(1)若 ,试判断 的形状,并说明理由;
(2)若 ,则 的面积为 ,求 , 的值;
(3)若 为锐角三角形,求 的取值范围.
19. “费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:
在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.意大利
数学家托里拆利给出了解答,当 的三个内角均小于 时,使得
的点 即为费马点;当 有一个内角大于
或等于 时,最大内角的顶点为费马点.试用以上知识解决下面的问题:
(1)若 是边长为的 6等边三角形,求该三角形的费马点 到各顶点的距离
之和;
(2) 的内角 , , 所对的边分别为 , , ,且 ,点 为 的
费马点.
(i)若 ,求 ;
(ii)求 的最小值.
山西省山西大学附属中学校 2024-2025 学年高一下学期期中考试数学试题
整体难度:适中
考试范围:复数、平面向量、空间向量与立体几何、三角函数与解三角形、等式与不等式
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 2
较易 7
适中 9
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 求复数的实部与虚部;复数代数形式的乘法运算
2 0.65 向量加法法则的几何应用;向量减法法则的几何应用
3 0.94 棱锥的结构特征和分类;棱台的结构特征和分类
4 0.85 数量积的坐标表示;求投影向量
5 0.65 余弦定理解三角形;已知模求数量积
向量的线性运算的几何应用;平面向量基本定理的应用;平面向量共线定理的推
6 0.4
论
7 0.85 台体体积的有关计算;球的体积的有关计算;求组合体的体积
8 0.65 求 cosx(型)函数的值域;数量积的运算律;向量加法法则的几何应用
二、多选题
9 0.85 斜二测画法中有关量的计算;由直观图还原几何图形
棱柱的展开图及最短距离问题;正棱锥及其有关计算;求组合多面体的表面积;
10 0.65
求组合体的体积
11 0.65 余弦定理解三角形;用向量解决线段的长度问题
三、填空题
12 0.85 与复数模相关的轨迹(图形)问题
13 0.85 球的截面的性质及计算;锥体体积的有关计算;球的表面积的有关计算
用和、差角的正切公式化简、求值;正弦定理解三角形;高度测量问题;基本不
14 0.65
等式求和的最小值
四、解答题
向量夹角的计算;向量垂直的坐标表示;由向量共线(平行)求参数;坐标计算
15 0.65
向量的模
复数代数形式的乘法运算;复数的除法运算;求复数的模;共轭复数的概念及计
16 0.85
算
多面体与球体内切外接问题;求组合体的体积;柱体体积的有关计算;球的表面
17 0.65
积的有关计算
三角形面积公式及其应用;正弦定理边角互化的应用;余弦定理解三角形;正、
18 0.85
余弦定理判定三角形形状
三角形面积公式及其应用;余弦定理解三角形;用定义求向量的数量积;基本不
19 0.65
等式求和的最小值
知识点分析
序号 知识点 对应题号
1 复数 1,12,16
2 平面向量 2,4,5,6,8,11,15,19
3 空间向量与立体几何 3,7,9,10,13,17
4 三角函数与解三角形 5,8,11,14,18,19
5 等式与不等式 14,19
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
