人教版五年级下册数学分数通分以及找几个数的最小公倍数的方法课件(共14张PPT)
文档属性
| 名称 | 人教版五年级下册数学分数通分以及找几个数的最小公倍数的方法课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 605.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 09:37:20 | ||
图片预览




文档简介
(共14张PPT)
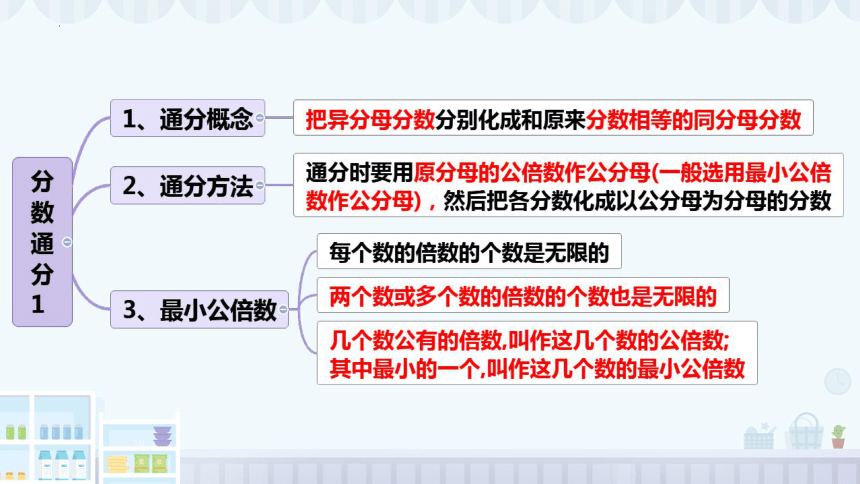
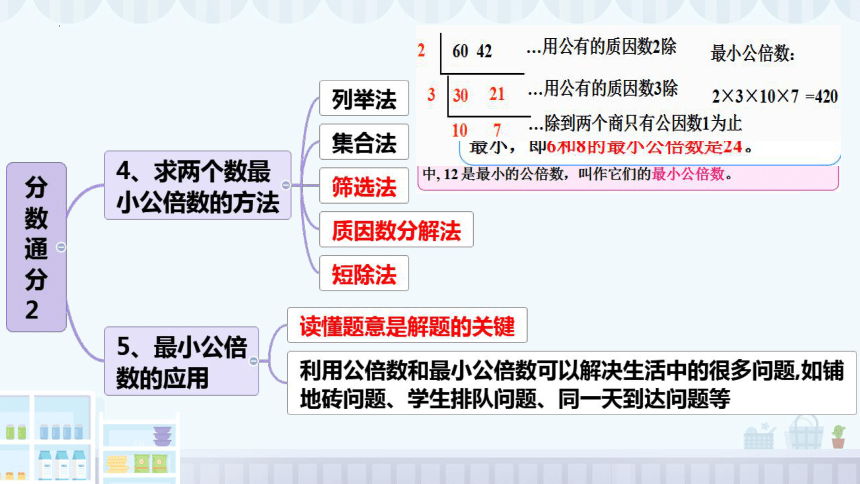
分数通分以及找几个数的最小公倍数的方法
二、课堂练习
1、请找出下列每组数据的最小公倍数。
4和12 6和9
2 4 12
2 2 6
1 3
4和12的最小公倍数是12.
3 6 9
2 3
6和9的最小公倍数=3X2X3=18.
二、课堂练习
1、请找出下列每组数据的最小公倍数。
11和17 12和18
11和17互质,所以11和17的最小公倍数=11X17=187.
2 12 18
3 6 9
2 3
12和18的最小公倍数是36.
二、课堂练习
1、请找出下列每组数据的最小公倍数。
16和24 18和24
2 16 24
2 8 12
2 4 6
2 3
16和24的最小公倍数是48.
2 18 24
3 9 12
3 4
18和24的最小公倍数是72.
2、30以内既是4的倍数,又是5的倍数的数是( )。
3、100以内既是10的倍数又是12的倍数的数是( )。
4、a和b是两个连续的非零自然数,它们的最小公倍数是( ) 。一个分数的分子和分母同时除以3,得到 ,原分数的分子和分母的最大公因数是( )。
5、一个数被3除余2,被7除也余2,这个数最小是( )。
6、一个三位数同时是3和5的倍数,这个三位数最小是( )。
7、两个质数的最小公倍数是77,这两个质数的和是( )。
20
60
ab
6
23
105
18
8、用长20cm、宽8cm的瓷砖贴一块正方形墙面,如果这块正方形墙面刚好由完整的这样的瓷砖贴成,这块正方形墙面边长最小是多少厘米?需要几块这样的瓷砖才能贴成?
2 20 8
2 10 4
5 2
20和8的最小公倍数=2×2×5×2=40.
40÷20=2(块),40÷8=5(块),则
2×5=10(块)
答:这块正方形墙面边长最小是40厘米;需要10块这样的瓷砖才能贴成。
9、五年级同学栽花,按12人一组或按15人一组都能正好分完.五年级参加栽花的至少有多少人?
3 12 15
4 5
12和15的最小公倍数=3×4×5=60.
答:五年级参加栽花的至少有60人。
10、五年级同学做操,按每8人一行,10人一行或12人一行,都正好排成整 旋转行而没有剩余,五年级至少有多少人?
求五年级至少有多少人,即求8、10、12三个数的最小公倍数,则
8=2×2×2
10=2×5
12=2×2×3
即8、10、12三个数的最小公倍数=2×2×2×5×3=120.
答:五年级至少有120人。
11、一些贝壳,4个4个地数,最后多1个;5个5个地数,最后多2个;6个6个数,最后多3个,这些贝壳至少有多少个?
由题意可知:这些贝壳加上3个就是4、5、6的公倍数,要求至少就是这些贝壳的个数是4、5、6的最小公倍数减去3,则
4=2×2,5=1×5,6=2×3,那么4、5、6的最小公倍数=2×2×5×3=60,则这些贝壳的个数=60-3=57(个)
答:这些贝壳至少有57个。
12、爸爸和他的同事张叔叔都参加了运动健身中心业余羽毛球锻炼,爸爸4天去一次,张叔叔6天去一次,5月1日他们同时在一起打球,几月几日他们会再次相遇?
2 4 6
2 3
4和6的最小公倍数=2×2×3=12.
1+12=13(日)
答:5月13日他们会再次相遇。
13、为了筹备毕业典礼座谈会,六(1)班的同学全部行动起来了.全班 的同学布置教室, 的同学采购物品,其余的准备汇报的节目.六(1)班最少有多少人?
全班 的同学布置教室, 的同学采购物品,所以班级人数必为9和5的倍数,因为9和5互质,所以9和5的最小公倍数=9×5=45,则六(1)班最少有45人。
答:六(1)班最少有45人。
14、大雪后的一天,小明与爸爸共同步测一个圆形花坛的周长,他们走的起点,路线,方向完全相同,小明的步长为54厘米,爸爸的步长为72厘米,由于两人脚印有重合,所以雪地里就留下60个脚印,这个花坛的周长是多少?
第一次两人脚印重合时,爸爸走的步数=216÷72=3(步),小明走的步数=216÷54=4(步),即爸爸3步与小明4步时脚印重合一次,此时有6个脚印,距离是216厘米。总共有60个脚印,应重合的次数=60÷6=10(次),则这条路长=216×10=2160(厘米)
答:这个花坛的周长是2160厘米。
2 54 72
3 27 36
3 9 12
3 4
54和72的最小公倍数=2×3×3×3×4=216.
分数通分以及找几个数的最小公倍数的方法
二、课堂练习
1、请找出下列每组数据的最小公倍数。
4和12 6和9
2 4 12
2 2 6
1 3
4和12的最小公倍数是12.
3 6 9
2 3
6和9的最小公倍数=3X2X3=18.
二、课堂练习
1、请找出下列每组数据的最小公倍数。
11和17 12和18
11和17互质,所以11和17的最小公倍数=11X17=187.
2 12 18
3 6 9
2 3
12和18的最小公倍数是36.
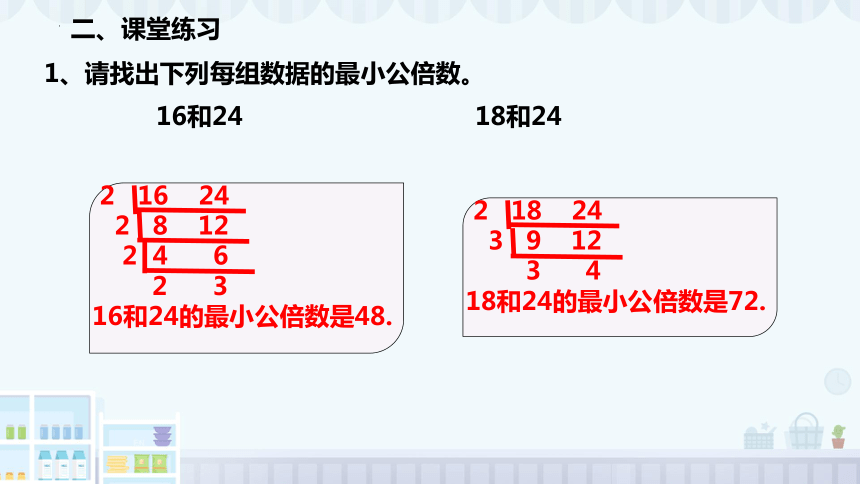
二、课堂练习
1、请找出下列每组数据的最小公倍数。
16和24 18和24
2 16 24
2 8 12
2 4 6
2 3
16和24的最小公倍数是48.
2 18 24
3 9 12
3 4
18和24的最小公倍数是72.
2、30以内既是4的倍数,又是5的倍数的数是( )。
3、100以内既是10的倍数又是12的倍数的数是( )。
4、a和b是两个连续的非零自然数,它们的最小公倍数是( ) 。一个分数的分子和分母同时除以3,得到 ,原分数的分子和分母的最大公因数是( )。
5、一个数被3除余2,被7除也余2,这个数最小是( )。
6、一个三位数同时是3和5的倍数,这个三位数最小是( )。
7、两个质数的最小公倍数是77,这两个质数的和是( )。
20
60
ab
6
23
105
18
8、用长20cm、宽8cm的瓷砖贴一块正方形墙面,如果这块正方形墙面刚好由完整的这样的瓷砖贴成,这块正方形墙面边长最小是多少厘米?需要几块这样的瓷砖才能贴成?
2 20 8
2 10 4
5 2
20和8的最小公倍数=2×2×5×2=40.
40÷20=2(块),40÷8=5(块),则
2×5=10(块)
答:这块正方形墙面边长最小是40厘米;需要10块这样的瓷砖才能贴成。
9、五年级同学栽花,按12人一组或按15人一组都能正好分完.五年级参加栽花的至少有多少人?
3 12 15
4 5
12和15的最小公倍数=3×4×5=60.
答:五年级参加栽花的至少有60人。
10、五年级同学做操,按每8人一行,10人一行或12人一行,都正好排成整 旋转行而没有剩余,五年级至少有多少人?
求五年级至少有多少人,即求8、10、12三个数的最小公倍数,则
8=2×2×2
10=2×5
12=2×2×3
即8、10、12三个数的最小公倍数=2×2×2×5×3=120.
答:五年级至少有120人。
11、一些贝壳,4个4个地数,最后多1个;5个5个地数,最后多2个;6个6个数,最后多3个,这些贝壳至少有多少个?
由题意可知:这些贝壳加上3个就是4、5、6的公倍数,要求至少就是这些贝壳的个数是4、5、6的最小公倍数减去3,则
4=2×2,5=1×5,6=2×3,那么4、5、6的最小公倍数=2×2×5×3=60,则这些贝壳的个数=60-3=57(个)
答:这些贝壳至少有57个。
12、爸爸和他的同事张叔叔都参加了运动健身中心业余羽毛球锻炼,爸爸4天去一次,张叔叔6天去一次,5月1日他们同时在一起打球,几月几日他们会再次相遇?
2 4 6
2 3
4和6的最小公倍数=2×2×3=12.
1+12=13(日)
答:5月13日他们会再次相遇。
13、为了筹备毕业典礼座谈会,六(1)班的同学全部行动起来了.全班 的同学布置教室, 的同学采购物品,其余的准备汇报的节目.六(1)班最少有多少人?
全班 的同学布置教室, 的同学采购物品,所以班级人数必为9和5的倍数,因为9和5互质,所以9和5的最小公倍数=9×5=45,则六(1)班最少有45人。
答:六(1)班最少有45人。
14、大雪后的一天,小明与爸爸共同步测一个圆形花坛的周长,他们走的起点,路线,方向完全相同,小明的步长为54厘米,爸爸的步长为72厘米,由于两人脚印有重合,所以雪地里就留下60个脚印,这个花坛的周长是多少?
第一次两人脚印重合时,爸爸走的步数=216÷72=3(步),小明走的步数=216÷54=4(步),即爸爸3步与小明4步时脚印重合一次,此时有6个脚印,距离是216厘米。总共有60个脚印,应重合的次数=60÷6=10(次),则这条路长=216×10=2160(厘米)
答:这个花坛的周长是2160厘米。
2 54 72
3 27 36
3 9 12
3 4
54和72的最小公倍数=2×3×3×3×4=216.
