人教版数学六年级下册典型应用题课件(共38张PPT)
文档属性
| 名称 | 人教版数学六年级下册典型应用题课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 09:51:53 | ||
图片预览








文档简介
(共38张PPT)
典型应用题
知识点1
归一、归总问题
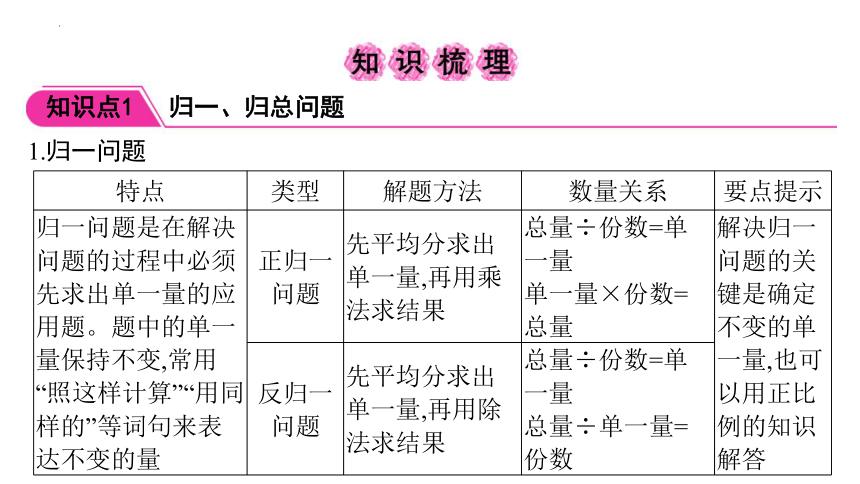
1.归一问题
特点 类型 解题方法 数量关系 要点提示
归一问题是在解决问题的过程中必须先求出单一量的应用题。题中的单一量保持不变,常用 “照这样计算”“用同样的”等词句来表达不变的量 正归一 问题 先平均分求出单一量,再用乘法求结果 总量÷份数=单一量 单一量×份数=总量 解决归一问题的关键是确定不变的单一量,也可以用正比例的知识解答
反归一 问题 先平均分求出单一量,再用除法求结果 总量÷份数=单一量 总量÷单一量=份数
2.归总问题
特点 解题方法 数量关系 要点提示
在解决问题的过程中必须先求出总量的应用题。题中的总数量保持不变 先求出总数量,再求未知数量 单一量×份数=总量 总量÷份数=单一量 总量÷单一量=份数 解决归总问题的关键是确定不变的总量,也可以用反比例的知识解答
知识点2
和差、和倍、差倍问题
类别 意义 数量关系
和差问题 已知两个数的和与差,求这两个数 (和+差)÷2=大数 大数-差=小数
(和-差)÷2=小数 小数+差=大数
和倍问题 已知两个数的和及它们之间的倍数关系,求这两个数 和÷(倍数+1)=小数(1倍数)
小数×倍数=大数(几倍数)
和-小数=大数
差倍问题 已知两个数的差及它们之间的倍数关系,求这两个数 差÷(倍数-1)=小数(1倍数)
小数×倍数=大数(几倍数)
差+小数=大数
知识点3
年龄问题
1.意义
已知两人或几人年龄之间的某些数量关系,求他们的年龄;或已知他们各自的年龄,求他们年龄之间的数量关系,这类问题一般称为年龄问题。
2.年龄问题中的规律
(1)两人年龄的差是不变的量。
(2)两人年龄的倍数关系是变化的量。
(3)两人年龄随着时间的增加都增加相等的岁数。
知识点4
工程问题
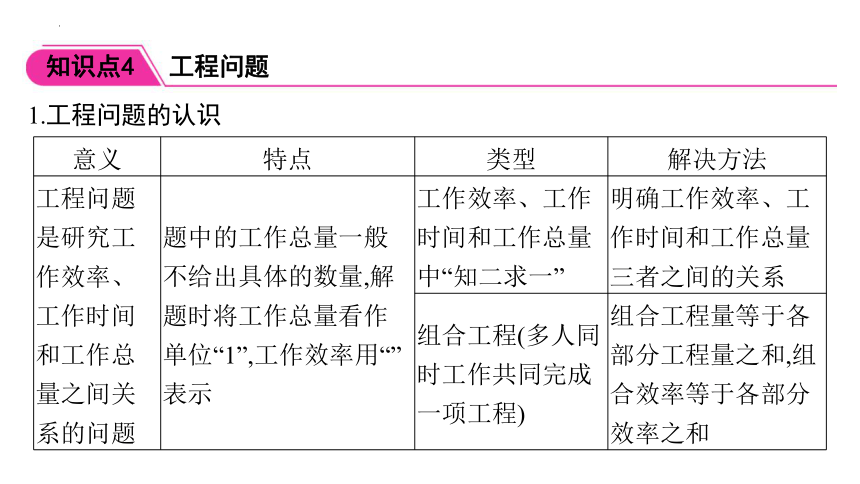
1.工程问题的认识
意义 特点 类型 解决方法
工程问题是研究工作效率、工作时间和工作总量之间关系的问题 题中的工作总量一般不给出具体的数量,解题时将工作总量看作单位“1”,工作效率用“”表示 工作效率、工作时间和工作总量中“知二求一” 明确工作效率、工作时间和工作总量三者之间的关系
组合工程(多人同时工作共同完成一项工程) 组合工程量等于各部分工程量之和,组合效率等于各部分效率之和
意义 特点 类型 解决方法
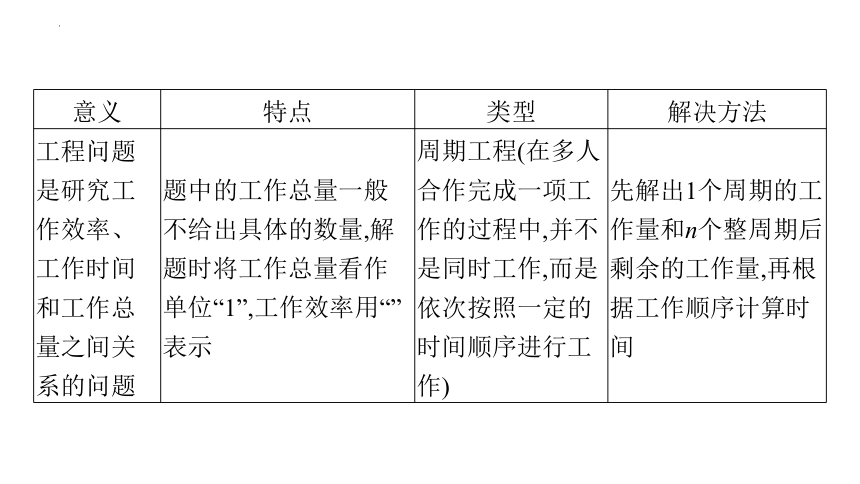
工程问题是研究工作效率、工作时间和工作总量之间关系的问题 题中的工作总量一般不给出具体的数量,解题时将工作总量看作单位“1”,工作效率用“”表示 周期工程(在多人合作完成一项工作的过程中,并不是同时工作,而是依次按照一定的时间顺序进行工作) 先解出1个周期的工作量和n个整周期后剩余的工作量,再根据工作顺序计算时间
意义 特点 类型 解决方法
工程问题是研究工作效率、工作时间和工作总量之间关系的问题 题中的工作总量一般不给出具体的数量,解题时将工作总量看作单位“1”,工作效率用“”表示 做做停停(一项工程本来由多人一起合作完成,合作一段时间后,突发状况,某一人离开,剩下的工程由其他人完成,求完成整个工作所需的时间) 先分别计算各阶段的工作量,再累加工作量得到总工作量,最后利用总工作量和相关条件求解具体问题
分配问题(主要涉及工程款的分配,分配的原则是按劳分配,根据工作量的比例关系来分配钱的多少,工作量大的分的钱就多) 确定总的工作量以及参与分配的各项工作的效率,再建立相应的等式
2.工程问题中的数量关系
(1)单人工程问题
工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
(2)合作工程问题
工作效率和×合作时间=工作总量 工作总量÷工作效率和=合作时间
工作总量÷合作时间=工作效率和 甲工作效率+乙工作效率=甲、乙工作效率和
知识点5
行程问题
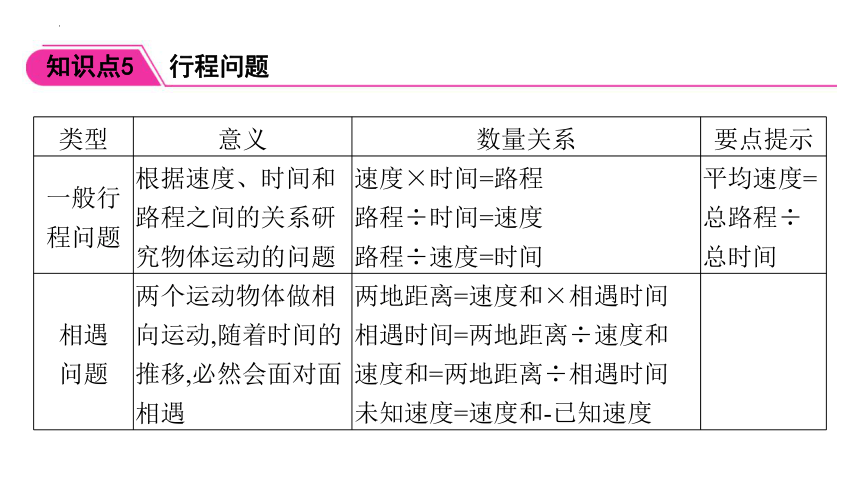
类型 意义 数量关系 要点提示
一般行程问题 根据速度、时间和路程之间的关系研究物体运动的问题 速度×时间=路程 路程÷时间=速度 路程÷速度=时间 平均速度=总路程÷总时间
相遇 问题 两个运动物体做相向运动,随着时间的推移,必然会面对面相遇 两地距离=速度和×相遇时间 相遇时间=两地距离÷速度和 速度和=两地距离÷相遇时间 未知速度=速度和-已知速度
类型 意义 数量关系 要点提示
追及 问题 两个运动物体在不同地点同时出发(或在同一地点不同时出发,或在不同地点不同时出发)做同向运动,后面的运动物体速度较快,前面的运动物体速度较慢,在一定时间之内,后面的运动物体会追上前面的运动物体 追及距离=速度差×追及时间 速度差=追及距离÷追及时间 追及时间=追及距离÷速度差 相遇问题和追及问题的关键词:同时、提前、相对开出、相向而行、背向而行等
类型 意义 数量关系 要点提示
火车行驶问题 火车在行驶中常有过桥与通过隧道、两车对开错车或快车超越慢车等情况。有路程、速度与时间之间的数量关系,同时还涉及车长、桥长等问题 (桥长+列车长)÷速度=过桥时间 火车过火车:反向,路程和=两车长;同向,路程差=两车长
类型 意义 数量关系 要点提示
流水行船问题 船在江河里航行时,除了本身的行进速度外,还受到流水的推送或阻挠,在这种情况下计算船的航行速度、时间和所行的路程的问题 顺水速度=船速+水速 逆水速度=船速-水速 船速=(顺水速度+逆水速度)÷2 水速=(顺水速度-逆水速度)÷2 可以将流水行船问题看作和差问题来解答,解题要以水速为线索
环形行程问题 两个运动物体在环形跑道以不同速度做背向或相向运动,随着时间的推移,必然会相遇或追及 相遇时间=环形周长÷速度和 追及时间=环形周长÷速度差 —
知识点6
浓度问题
1.意义
浓度问题是研究溶液、溶质、溶剂之间关系的问题。
2.类型
类型 意义 示例
溶质不变型 溶剂的增加或减少引起浓度的变化,始终不变的是溶质 向浓度为20%的盐水中加入50 g水
溶剂不变型 溶质的增加或减少引起浓度的变化,始终不变的是溶剂 向浓度为20%的盐水中加入5 g盐
配比型 两种或者几种不同浓度的溶液配比问题,混合前各溶液的溶质质量的和与混合后溶液的溶质质量相等 将100 g浓度为10%的盐水和100 g浓度为30%的盐水混合
3.数量关系
浓度=×100%=×100% 溶液质量=溶质质量÷浓度
溶剂质量=溶液质量-溶质质量=溶液质量×(1-浓度)
知识点7
盈亏问题
1.意义
在日常生活中,我们经常会将一定数量的物品平均分给一定数量的人。若每人少分一点,则物品有余(盈);若每人多分一点,则物品不够(亏)。根据分法的不同,得出所盈和所亏的数量,从而求得物品的数量和人数,像这一类问题叫盈亏问题。
2.类型
类型 意义 数量关系 要点提示
单盈问题 一次有余,另一次刚好够分 盈÷分配量之差=参与分配的份数 解决盈亏问题的关键在于找准分配和被分配的对象,有些题目是把人分配到物上,如乘车、乘船、分座位等
单亏问题 一次不足,另一次刚好够分 亏÷分配量之差=参与分配的份数
盈亏问题 一次有余,另一次不足 (盈+亏)÷分配量之差=参与分配的份数
双盈问题 第一次有余,第二次也有余 两盈之差÷分配量之差=参与分配的份数
双亏问题 第一次不足,第二次也不足 两亏之差÷分配量之差=参与分配的份数
刘老师去买书,买4本故事书和8本漫画书一共需要136元,买同样的3本故事书和10本漫画书一共需要150元。则买8本故事书和4本漫画书一共需要多少元
【分析】4本故事书和8本漫画书一共需要136元,将这些书按照1本故事书和2本漫画书为1份,可以分成4份,每一份是(136÷4)元,那么3本故事书和6本漫画书就是(136÷4×3)元。3本故事书和10本漫画书一共需要150元,两者相差了(150-136÷4×3)元,则(150-136÷4×3)元就是相差的4本漫画书的钱,据此先求出1本漫画书的价钱,再根据条件求出1本故事书的价钱,最后求出8本故事书和4本漫画书的价钱。
考 点
归一、归总问题(★★★★★)
1
例1
漫画书: (150-136÷4×3)÷4=(150-34×3)÷4=(150-102)÷4=48÷4=12(元) 故事书: (136-8×12)÷4=(136-96)÷4=40÷4=10(元)
8×10+4×12
=80+48
=128(元)
答:买8本故事书和4本漫画书一共需要128元。
1.一台冰箱5天耗电2.75千瓦时,照这样计算,这台冰箱8月份耗电( )千瓦时。
2.为响应习总书记“义务植树”的号召,学校一共买来800棵小树苗,同学们4天一共植树320棵。照这样计算,还要多少天才能把小树苗都植完
800÷(320÷4)=800÷80=10(天)
10-4=6(天)
答:还要6天才能把小树苗都植完。
17.05
3.[新情境]湘鄂川革命根据地纪念馆是我国第二批全国爱国主义教育基地。为缅怀先烈功绩,弘扬革命精神,纪念馆计划雕刻人物浮雕墙,计划每天雕刻28平方米的墙面,5.5天就能完工,实际提前了1天半,实际每天比计划多雕刻多少平方米墙面
28×5.5÷(5.5-1.5)=154÷4=38.5(平方米)
38.5-28=10.5(平方米)
答:实际每天比计划多雕刻10.5平方米墙面。
实验一小、实验二小两校一共有学生2346人,如果实验一小增加146人,实验二小减少88人,两校的学生人数就相等。这两个学校实际分别有多少人
【分析】根据“如果实验一小增加146人,实验二小减少88人,两校的学生人数就相等”可知,在实验一小人数没有增加,实验二小人数没有减少之前,两校的人数相差(146+88)人,则根据(和+差)÷2=大数可以求出实验二小实际的人数,进而求出实验一小实际的人数。
实验二小:(2346+146+88)÷2=2580÷2=1290(人)
实验一小: 2346-1290=1056(人)
答:实验一小实际有1056人,实验二小实际有1290人。
考 点
和差、和倍、差倍问题(★★★★★)
2
例2
4.功夫熊猫阿宝一天早晨、中午和晚上一共吃了80个包子,中午吃的个数是早晨的2倍,晚上吃的个数比早晨的2倍多5。那么阿宝这天中午吃了( )个包子。
5.两组学生参加义务劳动,甲组学生人数是乙组的3倍,而乙组的学生人数比甲组的3倍少40。求参加义务劳动的学生一共有( )人。
6.商店运来橘子、苹果、香蕉共53千克,橘子的质量比苹果的3倍少3千克,香蕉的质量比苹果的2倍多2千克。橘子重多少千克
(53+3-2)÷(3+2+1)=54÷6=9(千克)
9×3-3=27-3=24(千克)
答:橘子重24千克。
30
20
上学的路上,湘湘听到两个人在谈论各自的年龄,只听一人说“当我的年龄是你现在的年龄时,你才4岁”,另一人说“当我的年龄是你现在的年龄时,你将是61岁”。他们两人中,年龄较小的现在( )岁。
【解析】根据两人的年龄差一定可知,现在小年龄比年龄差大4岁,大年龄比年龄差大小年龄。当小年龄是大年龄现在的年龄时,大年龄将是61岁,就是再过一个年龄差,是61岁,61-4=57(岁),即57岁是3个年龄差,则年龄差为57÷3=19(岁),故年龄较小的现在的年龄为19+4=23(岁)。
考 点
年龄问题(★★★☆☆)
3
例3
23
7.五位老人的年龄之和是423岁,他们的年龄都取整数,并且各不相同,他们当中年龄最大的人最小可能是( )岁。
87
一件工程,乙队先做4天,甲、丙两队再合作6天,剩下的工程甲队单独做9天完成。已知乙队完成的是甲队完成的,丙队完成的是乙队完成的2倍,则甲、乙、丙三队单独做各需要多少天
【分析】先把甲完成的工作量看作单位“1”,则乙完成的工作量是,丙完成的工作量是,求出这项工程的总工作量;再根据“工作时间=工作量÷工作效率”列式计算。
考 点
工程问题(★★★★★)
4
例4
把甲完成的工作量看作单位“1”,则乙完成的工作量是
,
所以这项工程的总工作量为1+=2。
由题意可知,甲一共做了6+9=15(天),乙做了4天,丙做了6天。
甲: 15÷(1÷2)=15÷
=18(天)
答:甲单独做需要30天,乙单独做需要24天,丙单独做需要18天。
8.一个水池可以容水36立方米,有两个注水管注水。如果单开甲管6小时就可以注满;如果单开乙管4小时就可以注满。现在同时打开两个注水管向这个水池注水,( )小时后可以注满这个水池的;此时甲管注水( )立方米。
9.某服装工厂生产一批衣服,甲车间单独生产需要12天完成,乙车间单独生产需要30天完成。甲车间单独生产几天后由于机器故障,剩下的衣服全部由乙车间单独生产,从开始到完成生产共用15天。甲车间单独生产了几天 (用方程解答)
2
12
解:设甲车间单独生产了x天,则乙车间单独生产了(15-x)天。
×(15-x)=1
x=1
x=10
答:甲车间单独生产了10天。
10.修一条水渠,甲队单独修15天完成,乙队单独修2天修了全长的。现在甲队先修5天,乙队再加入一起修。完成工程后,两队共得工资3000元。按工作量分配甲队应得多少元
甲队的工作效率:1÷15=
乙队的工作效率:
甲、乙两队合作的工作时间:
×6=4(天)
×3000=1800(元)
答:按工作量分配甲队应得1800元。
英子和奶奶去操场上散步,奶奶走一圈需要12分钟,英子走一圈需要6分钟。如果两人同时从同一个地方出发,相背而行,相遇时她们走了( )分钟。
【解析】先把操场一圈的长度看作单位“1”,根据速度=路程÷时间,得到奶奶的速度为1÷12=,英子的速度为1÷6=;再根据相遇时间=路程÷速度和,得到相遇时间为1÷=4(分)。
考 点
行程问题(★★★★★)
5
例5
4
11.某铁路桥长2000米,一列火车从桥上通过,测得火车从开始上桥到完全下桥共用120秒,整列火车完全在桥上的时间为80秒。则火车的速度是( )米/秒。
12.甲、乙两人同时由A地出发到B地,甲骑自行车每分钟250米,乙步行每分钟90米,甲骑自行车到达B地后立即返回A地,在离B地3200米处与乙相遇。A,B两地相距( )米。
13.小赵早上以每分钟50米的速度从家向学校出发,12分钟后,小赵的爸爸发现小赵没有带文具盒,骑自行车以每分钟110米的速度去追小赵。爸爸( )分钟后能追上小赵。
20
6800
10
14.一艘船往返于甲、乙两地共用10小时,前5小时比后5小时多行驶80千米,顺流比逆流每小时多行驶20千米。则甲、乙两地相距多少千米
顺流的行驶时间:80÷20=4(时)
逆流的行驶时间:10-4=6(时)
把甲、乙两地的距离看作单位“1”,则顺流速度为。
20÷=240(千米)
答:甲、乙两地相距240千米。
一杯糖水,第一次加入一定量的水后,糖水的含糖百分比为15%;第二次又加入同样多的水,糖水的含糖百分比变为12%;第三次再加入同样多的水,糖水的含糖百分比将变为( )。
【解析】第一次加水后含糖百分比为15%,即糖占15份,水占85份,共100份。第二次又加入同样多的水,糖水的含糖百分比变为12%,则原来的15份糖的浓度变成了12%,所以此时的糖水份数为15÷12%=125,125-100=25,即每次加了25份水。根据浓度=×100%,得到第三次加水后的含糖百分比是×100%=10%。
考 点
浓度问题(★★★★☆)
6
例6
10%
15.现在有浓度为20%的酒精溶液300克,要把它变成浓度为40%的酒精溶液,需要加纯酒精( )克。
16.现有浓度为10%的盐水20千克,再加入多少千克浓度为30%的盐水,可以得到浓度为22%的盐水
20×(22%-10%)÷(30%-22%)
=20×12%÷8%
=2.4÷0.08
=30(千克)
答:再加入30千克浓度为30%的盐水,可以得到浓度为22%的盐水。
100
[传统文化]清明节,又称踏青节、三月节等,是“二十四节气”之一,也是传统祭祖节日,扫墓祭祖、踏青郊游是清明节的基本主题。放假前,孙老师给数学小组的同学准备了青团。若每人发10个,则还差32个;若每人发6个,则刚好分完。那么数学小组一共有多少名同学 孙老师一共准备了多少个青团
【分析】本题属于盈亏问题,两次分配时,人数和青团数量不变。第一次差32个,第二次刚好分完,可认为差0个,看作“双亏型”盈亏问题进行求解。
考 点
盈亏问题(★★★☆☆)
7
例7
32÷(10-6)
=32÷4
=8(名)
6×8=48(个)
答:数学小组一共有8名同学,孙老师一共准备了48个青团。
17.[新角度]某玻璃厂托运玻璃250箱,合同规定每箱运费20元,如果损坏一箱,不但不付运费还要赔偿100元。运后结算时,共付运费4400元。托运中损坏了( )箱玻璃。
5
典型应用题
知识点1
归一、归总问题
1.归一问题
特点 类型 解题方法 数量关系 要点提示
归一问题是在解决问题的过程中必须先求出单一量的应用题。题中的单一量保持不变,常用 “照这样计算”“用同样的”等词句来表达不变的量 正归一 问题 先平均分求出单一量,再用乘法求结果 总量÷份数=单一量 单一量×份数=总量 解决归一问题的关键是确定不变的单一量,也可以用正比例的知识解答
反归一 问题 先平均分求出单一量,再用除法求结果 总量÷份数=单一量 总量÷单一量=份数
2.归总问题
特点 解题方法 数量关系 要点提示
在解决问题的过程中必须先求出总量的应用题。题中的总数量保持不变 先求出总数量,再求未知数量 单一量×份数=总量 总量÷份数=单一量 总量÷单一量=份数 解决归总问题的关键是确定不变的总量,也可以用反比例的知识解答
知识点2
和差、和倍、差倍问题
类别 意义 数量关系
和差问题 已知两个数的和与差,求这两个数 (和+差)÷2=大数 大数-差=小数
(和-差)÷2=小数 小数+差=大数
和倍问题 已知两个数的和及它们之间的倍数关系,求这两个数 和÷(倍数+1)=小数(1倍数)
小数×倍数=大数(几倍数)
和-小数=大数
差倍问题 已知两个数的差及它们之间的倍数关系,求这两个数 差÷(倍数-1)=小数(1倍数)
小数×倍数=大数(几倍数)
差+小数=大数
知识点3
年龄问题
1.意义
已知两人或几人年龄之间的某些数量关系,求他们的年龄;或已知他们各自的年龄,求他们年龄之间的数量关系,这类问题一般称为年龄问题。
2.年龄问题中的规律
(1)两人年龄的差是不变的量。
(2)两人年龄的倍数关系是变化的量。
(3)两人年龄随着时间的增加都增加相等的岁数。
知识点4
工程问题
1.工程问题的认识
意义 特点 类型 解决方法
工程问题是研究工作效率、工作时间和工作总量之间关系的问题 题中的工作总量一般不给出具体的数量,解题时将工作总量看作单位“1”,工作效率用“”表示 工作效率、工作时间和工作总量中“知二求一” 明确工作效率、工作时间和工作总量三者之间的关系
组合工程(多人同时工作共同完成一项工程) 组合工程量等于各部分工程量之和,组合效率等于各部分效率之和
意义 特点 类型 解决方法
工程问题是研究工作效率、工作时间和工作总量之间关系的问题 题中的工作总量一般不给出具体的数量,解题时将工作总量看作单位“1”,工作效率用“”表示 周期工程(在多人合作完成一项工作的过程中,并不是同时工作,而是依次按照一定的时间顺序进行工作) 先解出1个周期的工作量和n个整周期后剩余的工作量,再根据工作顺序计算时间
意义 特点 类型 解决方法
工程问题是研究工作效率、工作时间和工作总量之间关系的问题 题中的工作总量一般不给出具体的数量,解题时将工作总量看作单位“1”,工作效率用“”表示 做做停停(一项工程本来由多人一起合作完成,合作一段时间后,突发状况,某一人离开,剩下的工程由其他人完成,求完成整个工作所需的时间) 先分别计算各阶段的工作量,再累加工作量得到总工作量,最后利用总工作量和相关条件求解具体问题
分配问题(主要涉及工程款的分配,分配的原则是按劳分配,根据工作量的比例关系来分配钱的多少,工作量大的分的钱就多) 确定总的工作量以及参与分配的各项工作的效率,再建立相应的等式
2.工程问题中的数量关系
(1)单人工程问题
工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
(2)合作工程问题
工作效率和×合作时间=工作总量 工作总量÷工作效率和=合作时间
工作总量÷合作时间=工作效率和 甲工作效率+乙工作效率=甲、乙工作效率和
知识点5
行程问题
类型 意义 数量关系 要点提示
一般行程问题 根据速度、时间和路程之间的关系研究物体运动的问题 速度×时间=路程 路程÷时间=速度 路程÷速度=时间 平均速度=总路程÷总时间
相遇 问题 两个运动物体做相向运动,随着时间的推移,必然会面对面相遇 两地距离=速度和×相遇时间 相遇时间=两地距离÷速度和 速度和=两地距离÷相遇时间 未知速度=速度和-已知速度
类型 意义 数量关系 要点提示
追及 问题 两个运动物体在不同地点同时出发(或在同一地点不同时出发,或在不同地点不同时出发)做同向运动,后面的运动物体速度较快,前面的运动物体速度较慢,在一定时间之内,后面的运动物体会追上前面的运动物体 追及距离=速度差×追及时间 速度差=追及距离÷追及时间 追及时间=追及距离÷速度差 相遇问题和追及问题的关键词:同时、提前、相对开出、相向而行、背向而行等
类型 意义 数量关系 要点提示
火车行驶问题 火车在行驶中常有过桥与通过隧道、两车对开错车或快车超越慢车等情况。有路程、速度与时间之间的数量关系,同时还涉及车长、桥长等问题 (桥长+列车长)÷速度=过桥时间 火车过火车:反向,路程和=两车长;同向,路程差=两车长
类型 意义 数量关系 要点提示
流水行船问题 船在江河里航行时,除了本身的行进速度外,还受到流水的推送或阻挠,在这种情况下计算船的航行速度、时间和所行的路程的问题 顺水速度=船速+水速 逆水速度=船速-水速 船速=(顺水速度+逆水速度)÷2 水速=(顺水速度-逆水速度)÷2 可以将流水行船问题看作和差问题来解答,解题要以水速为线索
环形行程问题 两个运动物体在环形跑道以不同速度做背向或相向运动,随着时间的推移,必然会相遇或追及 相遇时间=环形周长÷速度和 追及时间=环形周长÷速度差 —
知识点6
浓度问题
1.意义
浓度问题是研究溶液、溶质、溶剂之间关系的问题。
2.类型
类型 意义 示例
溶质不变型 溶剂的增加或减少引起浓度的变化,始终不变的是溶质 向浓度为20%的盐水中加入50 g水
溶剂不变型 溶质的增加或减少引起浓度的变化,始终不变的是溶剂 向浓度为20%的盐水中加入5 g盐
配比型 两种或者几种不同浓度的溶液配比问题,混合前各溶液的溶质质量的和与混合后溶液的溶质质量相等 将100 g浓度为10%的盐水和100 g浓度为30%的盐水混合
3.数量关系
浓度=×100%=×100% 溶液质量=溶质质量÷浓度
溶剂质量=溶液质量-溶质质量=溶液质量×(1-浓度)
知识点7
盈亏问题
1.意义
在日常生活中,我们经常会将一定数量的物品平均分给一定数量的人。若每人少分一点,则物品有余(盈);若每人多分一点,则物品不够(亏)。根据分法的不同,得出所盈和所亏的数量,从而求得物品的数量和人数,像这一类问题叫盈亏问题。
2.类型
类型 意义 数量关系 要点提示
单盈问题 一次有余,另一次刚好够分 盈÷分配量之差=参与分配的份数 解决盈亏问题的关键在于找准分配和被分配的对象,有些题目是把人分配到物上,如乘车、乘船、分座位等
单亏问题 一次不足,另一次刚好够分 亏÷分配量之差=参与分配的份数
盈亏问题 一次有余,另一次不足 (盈+亏)÷分配量之差=参与分配的份数
双盈问题 第一次有余,第二次也有余 两盈之差÷分配量之差=参与分配的份数
双亏问题 第一次不足,第二次也不足 两亏之差÷分配量之差=参与分配的份数
刘老师去买书,买4本故事书和8本漫画书一共需要136元,买同样的3本故事书和10本漫画书一共需要150元。则买8本故事书和4本漫画书一共需要多少元
【分析】4本故事书和8本漫画书一共需要136元,将这些书按照1本故事书和2本漫画书为1份,可以分成4份,每一份是(136÷4)元,那么3本故事书和6本漫画书就是(136÷4×3)元。3本故事书和10本漫画书一共需要150元,两者相差了(150-136÷4×3)元,则(150-136÷4×3)元就是相差的4本漫画书的钱,据此先求出1本漫画书的价钱,再根据条件求出1本故事书的价钱,最后求出8本故事书和4本漫画书的价钱。
考 点
归一、归总问题(★★★★★)
1
例1
漫画书: (150-136÷4×3)÷4=(150-34×3)÷4=(150-102)÷4=48÷4=12(元) 故事书: (136-8×12)÷4=(136-96)÷4=40÷4=10(元)
8×10+4×12
=80+48
=128(元)
答:买8本故事书和4本漫画书一共需要128元。
1.一台冰箱5天耗电2.75千瓦时,照这样计算,这台冰箱8月份耗电( )千瓦时。
2.为响应习总书记“义务植树”的号召,学校一共买来800棵小树苗,同学们4天一共植树320棵。照这样计算,还要多少天才能把小树苗都植完
800÷(320÷4)=800÷80=10(天)
10-4=6(天)
答:还要6天才能把小树苗都植完。
17.05
3.[新情境]湘鄂川革命根据地纪念馆是我国第二批全国爱国主义教育基地。为缅怀先烈功绩,弘扬革命精神,纪念馆计划雕刻人物浮雕墙,计划每天雕刻28平方米的墙面,5.5天就能完工,实际提前了1天半,实际每天比计划多雕刻多少平方米墙面
28×5.5÷(5.5-1.5)=154÷4=38.5(平方米)
38.5-28=10.5(平方米)
答:实际每天比计划多雕刻10.5平方米墙面。
实验一小、实验二小两校一共有学生2346人,如果实验一小增加146人,实验二小减少88人,两校的学生人数就相等。这两个学校实际分别有多少人
【分析】根据“如果实验一小增加146人,实验二小减少88人,两校的学生人数就相等”可知,在实验一小人数没有增加,实验二小人数没有减少之前,两校的人数相差(146+88)人,则根据(和+差)÷2=大数可以求出实验二小实际的人数,进而求出实验一小实际的人数。
实验二小:(2346+146+88)÷2=2580÷2=1290(人)
实验一小: 2346-1290=1056(人)
答:实验一小实际有1056人,实验二小实际有1290人。
考 点
和差、和倍、差倍问题(★★★★★)
2
例2
4.功夫熊猫阿宝一天早晨、中午和晚上一共吃了80个包子,中午吃的个数是早晨的2倍,晚上吃的个数比早晨的2倍多5。那么阿宝这天中午吃了( )个包子。
5.两组学生参加义务劳动,甲组学生人数是乙组的3倍,而乙组的学生人数比甲组的3倍少40。求参加义务劳动的学生一共有( )人。
6.商店运来橘子、苹果、香蕉共53千克,橘子的质量比苹果的3倍少3千克,香蕉的质量比苹果的2倍多2千克。橘子重多少千克
(53+3-2)÷(3+2+1)=54÷6=9(千克)
9×3-3=27-3=24(千克)
答:橘子重24千克。
30
20
上学的路上,湘湘听到两个人在谈论各自的年龄,只听一人说“当我的年龄是你现在的年龄时,你才4岁”,另一人说“当我的年龄是你现在的年龄时,你将是61岁”。他们两人中,年龄较小的现在( )岁。
【解析】根据两人的年龄差一定可知,现在小年龄比年龄差大4岁,大年龄比年龄差大小年龄。当小年龄是大年龄现在的年龄时,大年龄将是61岁,就是再过一个年龄差,是61岁,61-4=57(岁),即57岁是3个年龄差,则年龄差为57÷3=19(岁),故年龄较小的现在的年龄为19+4=23(岁)。
考 点
年龄问题(★★★☆☆)
3
例3
23
7.五位老人的年龄之和是423岁,他们的年龄都取整数,并且各不相同,他们当中年龄最大的人最小可能是( )岁。
87
一件工程,乙队先做4天,甲、丙两队再合作6天,剩下的工程甲队单独做9天完成。已知乙队完成的是甲队完成的,丙队完成的是乙队完成的2倍,则甲、乙、丙三队单独做各需要多少天
【分析】先把甲完成的工作量看作单位“1”,则乙完成的工作量是,丙完成的工作量是,求出这项工程的总工作量;再根据“工作时间=工作量÷工作效率”列式计算。
考 点
工程问题(★★★★★)
4
例4
把甲完成的工作量看作单位“1”,则乙完成的工作量是
,
所以这项工程的总工作量为1+=2。
由题意可知,甲一共做了6+9=15(天),乙做了4天,丙做了6天。
甲: 15÷(1÷2)=15÷
=18(天)
答:甲单独做需要30天,乙单独做需要24天,丙单独做需要18天。
8.一个水池可以容水36立方米,有两个注水管注水。如果单开甲管6小时就可以注满;如果单开乙管4小时就可以注满。现在同时打开两个注水管向这个水池注水,( )小时后可以注满这个水池的;此时甲管注水( )立方米。
9.某服装工厂生产一批衣服,甲车间单独生产需要12天完成,乙车间单独生产需要30天完成。甲车间单独生产几天后由于机器故障,剩下的衣服全部由乙车间单独生产,从开始到完成生产共用15天。甲车间单独生产了几天 (用方程解答)
2
12
解:设甲车间单独生产了x天,则乙车间单独生产了(15-x)天。
×(15-x)=1
x=1
x=10
答:甲车间单独生产了10天。
10.修一条水渠,甲队单独修15天完成,乙队单独修2天修了全长的。现在甲队先修5天,乙队再加入一起修。完成工程后,两队共得工资3000元。按工作量分配甲队应得多少元
甲队的工作效率:1÷15=
乙队的工作效率:
甲、乙两队合作的工作时间:
×6=4(天)
×3000=1800(元)
答:按工作量分配甲队应得1800元。
英子和奶奶去操场上散步,奶奶走一圈需要12分钟,英子走一圈需要6分钟。如果两人同时从同一个地方出发,相背而行,相遇时她们走了( )分钟。
【解析】先把操场一圈的长度看作单位“1”,根据速度=路程÷时间,得到奶奶的速度为1÷12=,英子的速度为1÷6=;再根据相遇时间=路程÷速度和,得到相遇时间为1÷=4(分)。
考 点
行程问题(★★★★★)
5
例5
4
11.某铁路桥长2000米,一列火车从桥上通过,测得火车从开始上桥到完全下桥共用120秒,整列火车完全在桥上的时间为80秒。则火车的速度是( )米/秒。
12.甲、乙两人同时由A地出发到B地,甲骑自行车每分钟250米,乙步行每分钟90米,甲骑自行车到达B地后立即返回A地,在离B地3200米处与乙相遇。A,B两地相距( )米。
13.小赵早上以每分钟50米的速度从家向学校出发,12分钟后,小赵的爸爸发现小赵没有带文具盒,骑自行车以每分钟110米的速度去追小赵。爸爸( )分钟后能追上小赵。
20
6800
10
14.一艘船往返于甲、乙两地共用10小时,前5小时比后5小时多行驶80千米,顺流比逆流每小时多行驶20千米。则甲、乙两地相距多少千米
顺流的行驶时间:80÷20=4(时)
逆流的行驶时间:10-4=6(时)
把甲、乙两地的距离看作单位“1”,则顺流速度为。
20÷=240(千米)
答:甲、乙两地相距240千米。
一杯糖水,第一次加入一定量的水后,糖水的含糖百分比为15%;第二次又加入同样多的水,糖水的含糖百分比变为12%;第三次再加入同样多的水,糖水的含糖百分比将变为( )。
【解析】第一次加水后含糖百分比为15%,即糖占15份,水占85份,共100份。第二次又加入同样多的水,糖水的含糖百分比变为12%,则原来的15份糖的浓度变成了12%,所以此时的糖水份数为15÷12%=125,125-100=25,即每次加了25份水。根据浓度=×100%,得到第三次加水后的含糖百分比是×100%=10%。
考 点
浓度问题(★★★★☆)
6
例6
10%
15.现在有浓度为20%的酒精溶液300克,要把它变成浓度为40%的酒精溶液,需要加纯酒精( )克。
16.现有浓度为10%的盐水20千克,再加入多少千克浓度为30%的盐水,可以得到浓度为22%的盐水
20×(22%-10%)÷(30%-22%)
=20×12%÷8%
=2.4÷0.08
=30(千克)
答:再加入30千克浓度为30%的盐水,可以得到浓度为22%的盐水。
100
[传统文化]清明节,又称踏青节、三月节等,是“二十四节气”之一,也是传统祭祖节日,扫墓祭祖、踏青郊游是清明节的基本主题。放假前,孙老师给数学小组的同学准备了青团。若每人发10个,则还差32个;若每人发6个,则刚好分完。那么数学小组一共有多少名同学 孙老师一共准备了多少个青团
【分析】本题属于盈亏问题,两次分配时,人数和青团数量不变。第一次差32个,第二次刚好分完,可认为差0个,看作“双亏型”盈亏问题进行求解。
考 点
盈亏问题(★★★☆☆)
7
例7
32÷(10-6)
=32÷4
=8(名)
6×8=48(个)
答:数学小组一共有8名同学,孙老师一共准备了48个青团。
17.[新角度]某玻璃厂托运玻璃250箱,合同规定每箱运费20元,如果损坏一箱,不但不付运费还要赔偿100元。运后结算时,共付运费4400元。托运中损坏了( )箱玻璃。
5
