人教A版高中数学选择性必修第一册1.4.1空间中点、直线和平面的向量表示(第1课时) 课件(共41张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.1空间中点、直线和平面的向量表示(第1课时) 课件(共41张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:35:15 | ||
图片预览






文档简介
(共41张PPT)
·选择性必修第一册·
第1课时 空间中点、直线和平面的向量表示
1
2
学习目标
课程标准要求:
能用向量语言描述直线和平面,理解直线的方向向量与平面的法向量。
课时目标要求:
(1)能用向量语言表示空间中的点、直线与平面.
(2)能用自己的语言解释直线的方向向量、平面的法向量的含义.
(3)能说出求解直线的方向向量与平面的法向量的一般步骤,会求直线的方向向量与平面的法向量.
引入新知
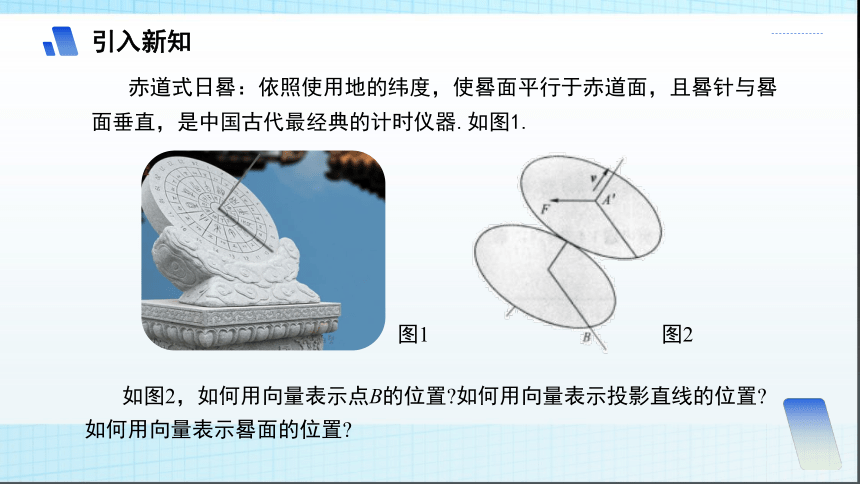
赤道式日晷:依照使用地的纬度,使晷面平行于赤道面,且晷针与晷面垂直,是中国古代最经典的计时仪器.如图1.
图1
图2
如图2,如何用向量表示点B的位置 如何用向量表示投影直线的位置 如何用向量表示晷面的位置
新课探究
我们知道,点、 直线和平面是空间的基本图形,点、 线段和平面图形等是组成空间几何体的基本元素因此,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、 直线和平面.
新课探究
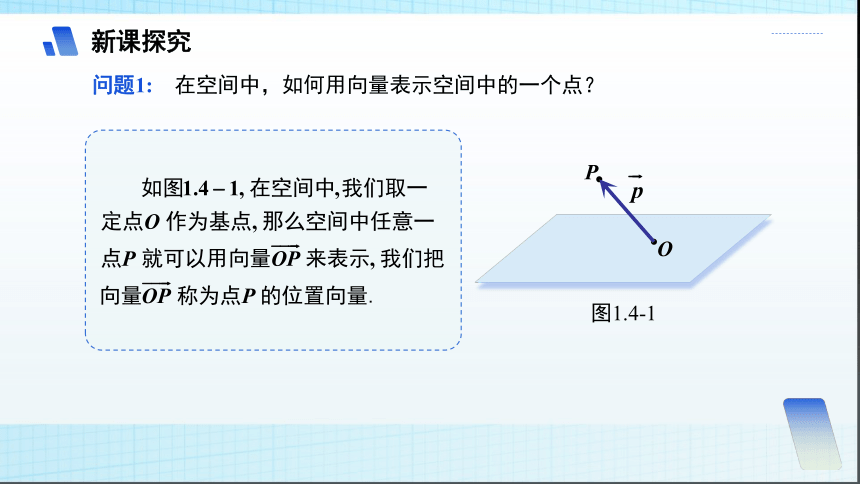
问题1: 在空间中,如何用向量表示空间中的一个点?
O
P
图1.4-1
新课探究
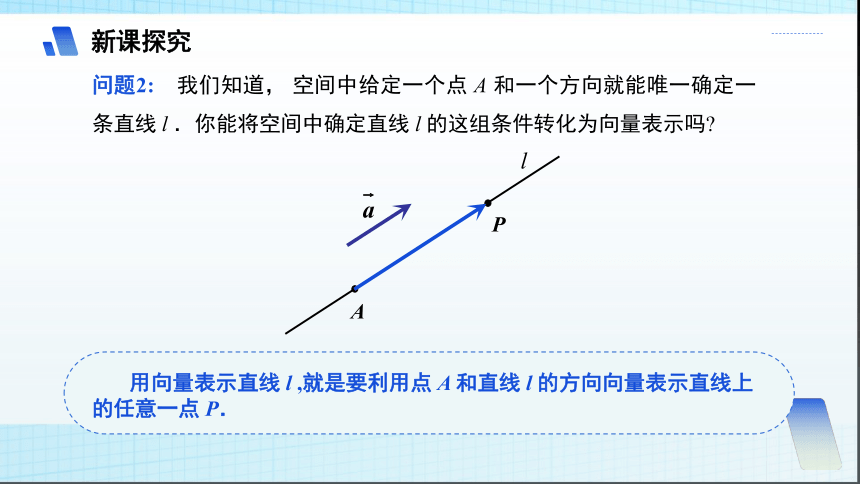
问题2: 我们知道, 空间中给定一个点 A 和一个方向就能唯一确定一条直线 l .你能将空间中确定直线 l 的这组条件转化为向量表示吗
A
P
l
用向量表示直线 l ,就是要利用点 A 和直线 l 的方向向量表示直线上的任意一点 P.
新课探究
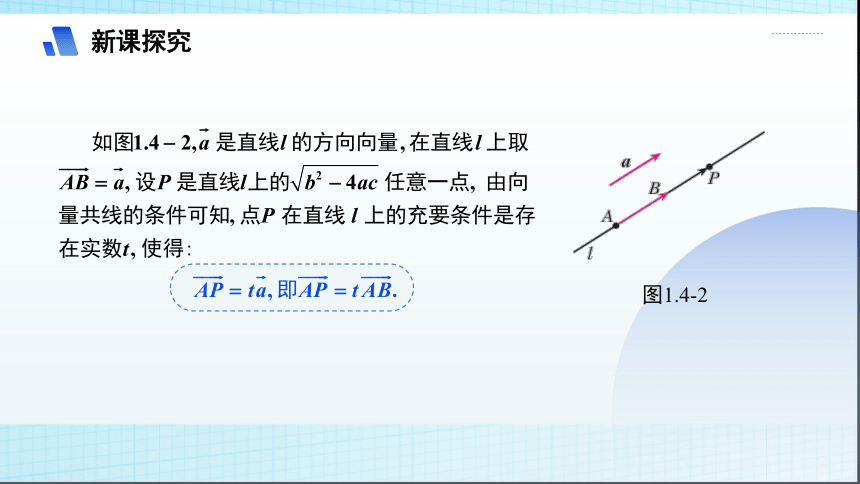
图1.4-2
新课探究
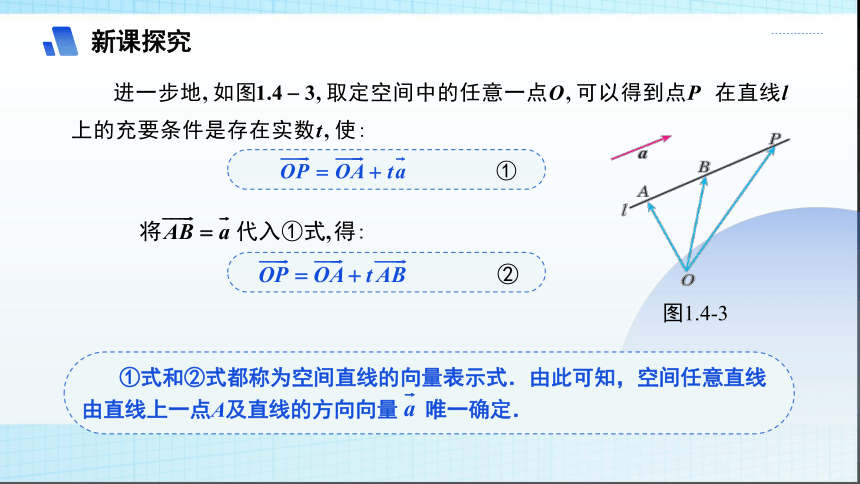
图1.4-3
①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点A及直线的方向向量 唯一确定.
新课探究
问题3: 我们知道,两条相交直线能确定一个平面,类比空间直线的向量表示,你能将上述确定一个平面的条件转化为向量表示吗
图1.4-4
新课探究
图1.4-5
我们把③式称为空间平面ABC的向量表示式.
由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
新课探究
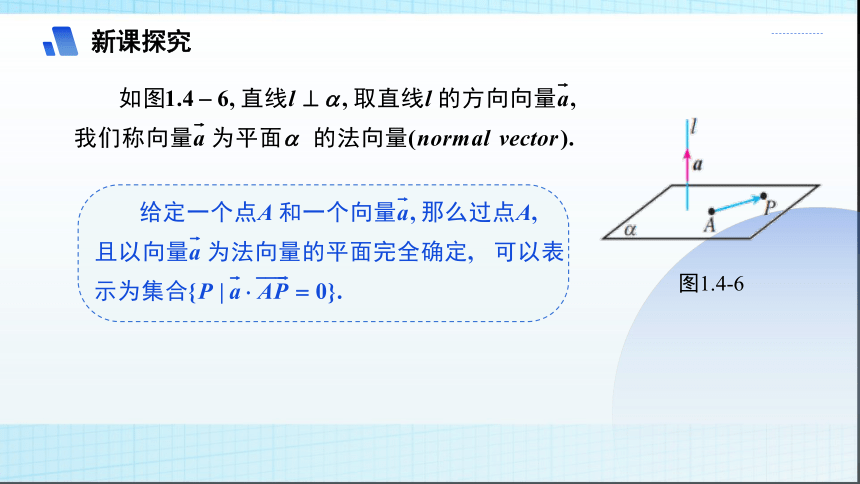
问题4: 给一个定点和一个定方向(向量),能确定一个平面在空间中的位置吗?
我们知道,给定空间一点 A 和一条直线 l ,则过点 A 且垂直于直线 l 的平面是唯一确定的.由此得到启发,我们可以利用点 A 和直线 l 的方向向量来确定平面.
新课探究
图1.4-6
新课探究
总结新知
空间中点线面的向量表示小结
l
A
P
应用新知
图1.4-7
应用新知
图1.4-7
应用新知
图1.4-7
应用新知
方法规律
应用新知
方法规律
求平面法向量的常见类型
(1)已知平面内三个点的坐标,求这三个点确定的平面的法向量;
(2)一个几何体中存在线面垂直关系,在建立空间直角坐标系后,平面的垂线的方向向量即为平面的法向量;
(3)在几何体中找到平面内已知点的坐标或找到与平面平行的向量,然后求平面的法向量.
应用新知
变式训练:
A
B
C
D
D1
A1
B1
C1
x
y
z
解:
应用新知
变式训练:
A
B
C
D
D1
A1
B1
C1
x
y
z
解:
应用新知
变式训练:
A
B
C
D
D1
A1
B1
C1
x
y
z
解:
能力提升
例题
题型一
利用空间直线的向量表示式解决问题
解析
能力提升
例题
题型一
利用空间直线的向量表示式解决问题
A
B
C
D
D1
A1
B1
C1
O
解析
能力提升
方法总结
能力提升
变式训练
题型一
利用空间直线的向量表示式解决问题
能力提升
题型一
利用空间直线的向量表示式解决问题
解析
能力提升
题型一
利用空间直线的向量表示式解决问题
解析
能力提升
例题
题型二
空间平面的向量表示式
解析
能力提升
例题
题型二
空间平面的向量表示式
解析
能力提升
方法总结
能力提升
方法总结
能力提升
变式训练
题型二
空间平面的向量表示式
解析
能力提升
题型二
空间平面的向量表示式
解析
变式训练
课堂小结
作业布置
巩固作业:教科书第29页练习第1题 ;
教科书第41页习题第1、2题.
作业答案(教科书第29页练习第1题)
解析
√
×
√
作业答案(教科书第41页习题1.4第1题)
解析
作业答案(教科书第41页习题1.4第1题)
解析
作业答案(教科书第41页习题1.4第2题)
解析
作业答案(教科书第41页习题1.4第2题)
解析
·选择性必修第一册·
第1课时 空间中点、直线和平面的向量表示
1
2
学习目标
课程标准要求:
能用向量语言描述直线和平面,理解直线的方向向量与平面的法向量。
课时目标要求:
(1)能用向量语言表示空间中的点、直线与平面.
(2)能用自己的语言解释直线的方向向量、平面的法向量的含义.
(3)能说出求解直线的方向向量与平面的法向量的一般步骤,会求直线的方向向量与平面的法向量.
引入新知
赤道式日晷:依照使用地的纬度,使晷面平行于赤道面,且晷针与晷面垂直,是中国古代最经典的计时仪器.如图1.
图1
图2
如图2,如何用向量表示点B的位置 如何用向量表示投影直线的位置 如何用向量表示晷面的位置
新课探究
我们知道,点、 直线和平面是空间的基本图形,点、 线段和平面图形等是组成空间几何体的基本元素因此,为了用空间向量解决立体几何问题,首先要用向量表示空间中的点、 直线和平面.
新课探究
问题1: 在空间中,如何用向量表示空间中的一个点?
O
P
图1.4-1
新课探究
问题2: 我们知道, 空间中给定一个点 A 和一个方向就能唯一确定一条直线 l .你能将空间中确定直线 l 的这组条件转化为向量表示吗
A
P
l
用向量表示直线 l ,就是要利用点 A 和直线 l 的方向向量表示直线上的任意一点 P.
新课探究
图1.4-2
新课探究
图1.4-3
①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点A及直线的方向向量 唯一确定.
新课探究
问题3: 我们知道,两条相交直线能确定一个平面,类比空间直线的向量表示,你能将上述确定一个平面的条件转化为向量表示吗
图1.4-4
新课探究
图1.4-5
我们把③式称为空间平面ABC的向量表示式.
由此可知,空间中任意平面由空间一点及两个不共线向量唯一确定.
新课探究
问题4: 给一个定点和一个定方向(向量),能确定一个平面在空间中的位置吗?
我们知道,给定空间一点 A 和一条直线 l ,则过点 A 且垂直于直线 l 的平面是唯一确定的.由此得到启发,我们可以利用点 A 和直线 l 的方向向量来确定平面.
新课探究
图1.4-6
新课探究
总结新知
空间中点线面的向量表示小结
l
A
P
应用新知
图1.4-7
应用新知
图1.4-7
应用新知
图1.4-7
应用新知
方法规律
应用新知
方法规律
求平面法向量的常见类型
(1)已知平面内三个点的坐标,求这三个点确定的平面的法向量;
(2)一个几何体中存在线面垂直关系,在建立空间直角坐标系后,平面的垂线的方向向量即为平面的法向量;
(3)在几何体中找到平面内已知点的坐标或找到与平面平行的向量,然后求平面的法向量.
应用新知
变式训练:
A
B
C
D
D1
A1
B1
C1
x
y
z
解:
应用新知
变式训练:
A
B
C
D
D1
A1
B1
C1
x
y
z
解:
应用新知
变式训练:
A
B
C
D
D1
A1
B1
C1
x
y
z
解:
能力提升
例题
题型一
利用空间直线的向量表示式解决问题
解析
能力提升
例题
题型一
利用空间直线的向量表示式解决问题
A
B
C
D
D1
A1
B1
C1
O
解析
能力提升
方法总结
能力提升
变式训练
题型一
利用空间直线的向量表示式解决问题
能力提升
题型一
利用空间直线的向量表示式解决问题
解析
能力提升
题型一
利用空间直线的向量表示式解决问题
解析
能力提升
例题
题型二
空间平面的向量表示式
解析
能力提升
例题
题型二
空间平面的向量表示式
解析
能力提升
方法总结
能力提升
方法总结
能力提升
变式训练
题型二
空间平面的向量表示式
解析
能力提升
题型二
空间平面的向量表示式
解析
变式训练
课堂小结
作业布置
巩固作业:教科书第29页练习第1题 ;
教科书第41页习题第1、2题.
作业答案(教科书第29页练习第1题)
解析
√
×
√
作业答案(教科书第41页习题1.4第1题)
解析
作业答案(教科书第41页习题1.4第1题)
解析
作业答案(教科书第41页习题1.4第2题)
解析
作业答案(教科书第41页习题1.4第2题)
解析
