人教A版高中数学选择性必修第一册1.3空间向量及其运算的坐标表示 课件(共57张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.3空间向量及其运算的坐标表示 课件(共57张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:36:19 | ||
图片预览





文档简介
(共57张PPT)
第一章 空间向量与立体几何1.3 空间向量及其坐标运算
·选择性必修第一册·
1
学习目标
了解空间向量基本定理及其意义,掌握空间向量的正交分解及其坐标表示。
掌握空间向量的线性运算及其坐标表示。
掌握空间向量的数量积及其坐标表示。
2
3
(一)课程标准要求
1
学习目标
2
3
(二)课时目标要求
4
理解空间直角坐标系,感受建立空间直角坐标系的必要性.
借助空间直角坐标系理解空间中点的坐标和向量的坐标的概念及坐标表示.
会用坐标表示空间向量的线性运算及数量积运算.
会利用空间向量运算的坐标表示解决一些简单的立体几何问题.
引入新知
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点排除了数量关系……对于集合,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法……”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
引入新知
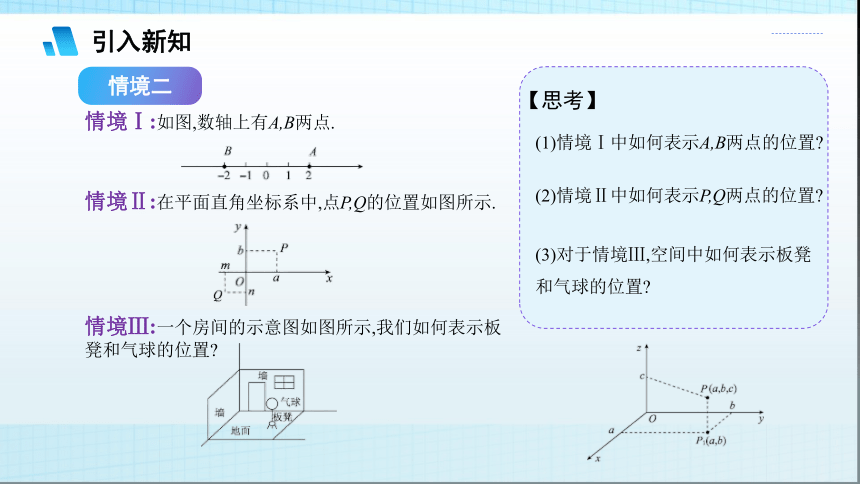
情境二
情境Ⅰ:如图,数轴上有A,B两点.
情境Ⅱ:在平面直角坐标系中,点P,Q的位置如图所示.
【思考】
(1)情境Ⅰ中如何表示A,B两点的位置
(2)情境Ⅱ中如何表示P,Q两点的位置
(3)对于情境Ⅲ,空间中如何表示板凳和气球的位置
情境Ⅲ:一个房间的示意图如图所示,我们如何表示板凳和气球的位置
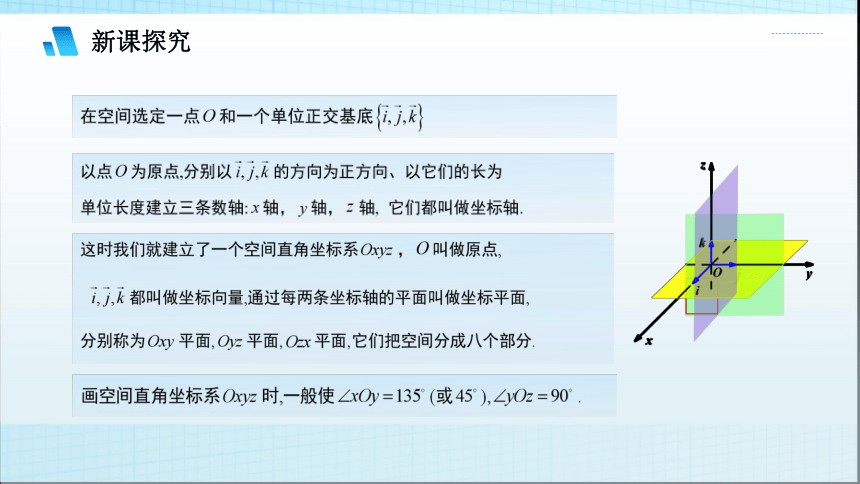
新课探究
问题1
我们是如何建立平面向量的坐标表示的 你能类比平面直角坐标系与平面向量单位正交基的关系,你能利用空间向量单位正交基底概念构建空间直角坐标系吗
x
y
O
i
j
新课探究
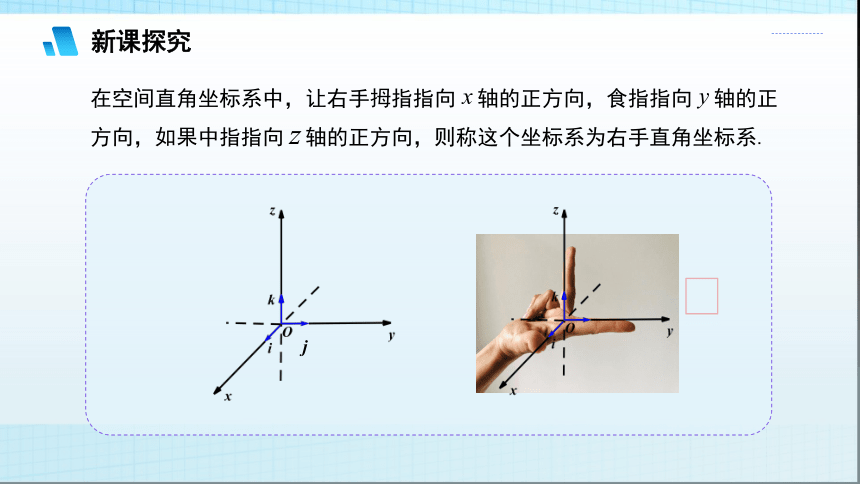
新课探究
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
新课探究
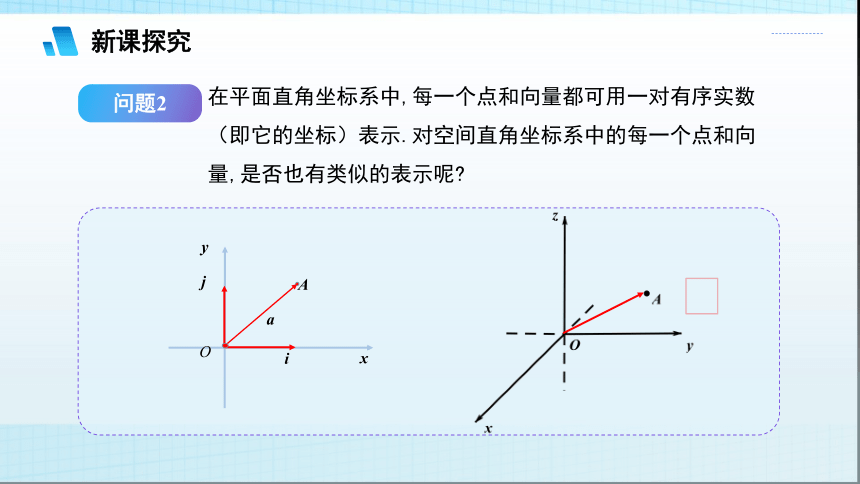
问题2
在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢
x
y
O
i
j
A
a
新课探究
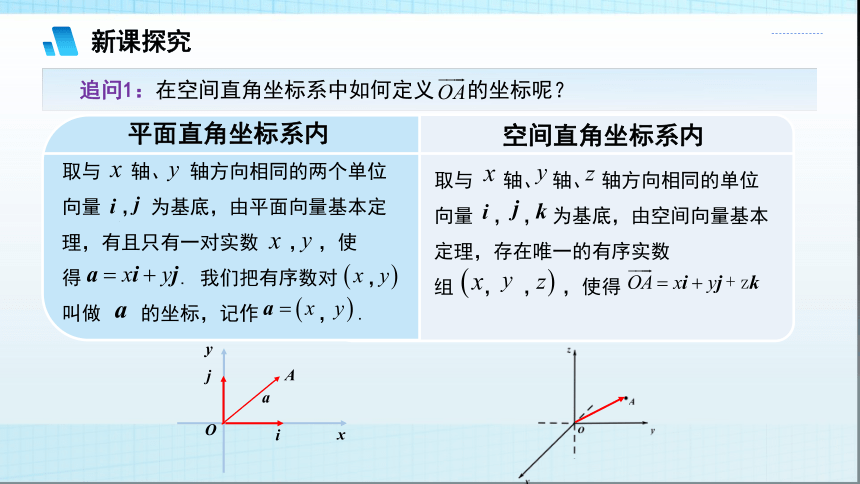
追问1:在空间直角坐标系中如何定义 的坐标呢?
x
y
O
i
j
a
A
平面直角坐标系内
空间直角坐标系内
取与 轴、 轴方向相同的两个单位向量 , 为基底,由平面向量基本定理,有且只有一对实数 , ,使得 . 我们把有序数对 , 叫做 的坐标,记作 , .
取与 轴、 轴、 轴方向相同的单位向量 , , 为基底,由空间向量基本定理,存在唯一的有序实数组 , , ,使得
新课探究
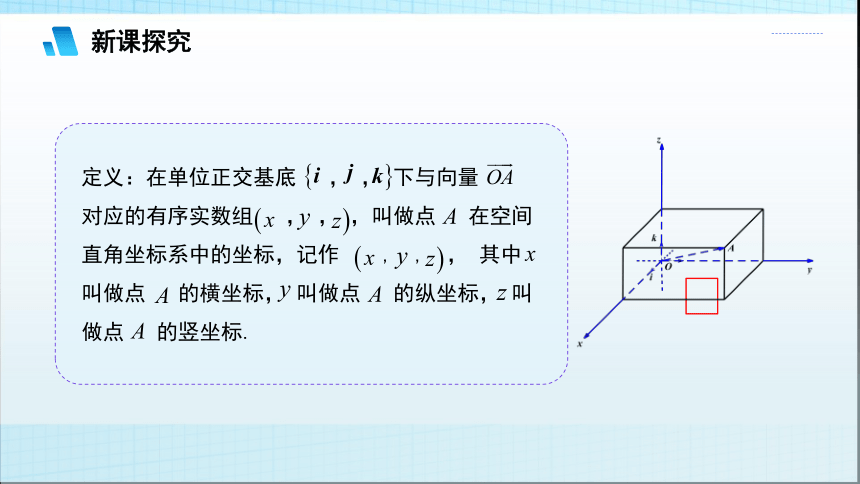
定义:在单位正交基底 , , 下与向量 对应的有序实数组 , , ,叫做点 在空间直角坐标系中的坐标,记作 , , , 其中 叫做点 的横坐标, 叫做点 的纵坐标, 叫做点 的竖坐标.
新课探究
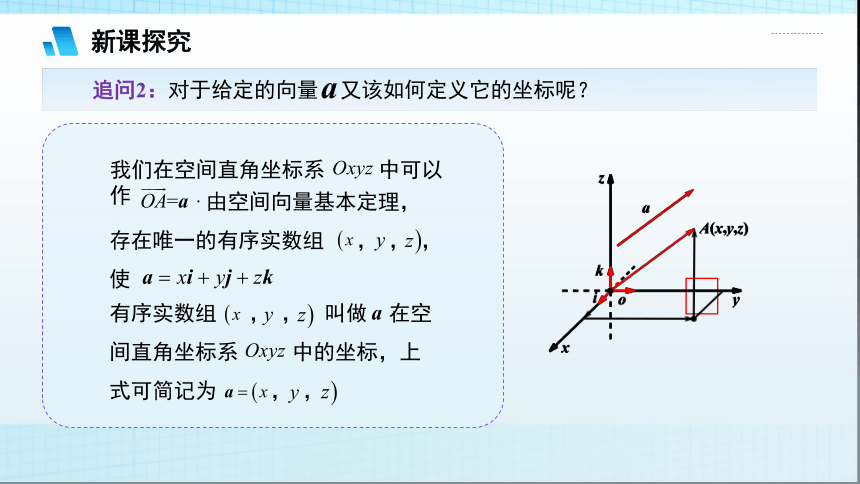
追问2:对于给定的向量 又该如何定义它的坐标呢?
我们在空间直角坐标系 中可以作 .
由空间向量基本定理,存在唯一的有序实数组 , , ,使
有序实数组 , , 叫做 在空间直角坐标系 中的坐标,上式可简记为 , ,
新课探究
问题3
在空间直角坐标系 中,对空间任意一点 ,或任意一个向量 ,你能借助几何直观确定它们的坐标 , , 吗?
过点 分别作垂直于 轴、 轴和 轴的平面
依次交 轴、 轴和 轴于点 , 和 .
即点 或者向量 的
坐标就是 , , .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
新课探究
问题4
有了空间向量的坐标表示,你能类比平面向量的坐标运算,得出空间向量运算的坐标表示并给出证明吗 请同学们类比平面向量运算的坐标表示研究空间向量运算的坐标表示,独立完成下列表格,并进行小组交流
新课探究
设
设
设
设
加法运算
减法运算
平面向量坐标运算
空间向量坐标运算
数乘运算
数量积运算
有向线段的向量坐标表示
线性运算
新课探究
下面我们证明空间向量数量积运算的坐标表示.
请同学们证明剩下运算的坐标表示
设 为空间的一个单位正交基底,
则
所以
因为
所以
新课探究
问题5
平面向量的坐标运算可以帮助我们解决平行、垂直等位置关系以及距离,角度等度量问题.空间向量的坐标运算是否仍然可以帮助我们解决这些问题?
新课探究
yOz平面
追问1:如何用平面向量的坐标运算刻画平面向量的平行和垂直?
平面向量的特殊位置关系
平面向量的特殊位置关系
设
当 时,
当 时,
设
能否表示为 ?
新课探究
当 时,
设
能否表示为 ?
至少一个不为0.
例如:当 与平面 平行时, .此时 无意义.
例如:当 与平面 平行时, .此时 无意义.
因此,只有 均不为0时,
特殊地, 与任意向量平行.
当 时,
新课探究
yOz平面
平面向量的特殊位置关系
空间向量的特殊位置关系
设
当 时,
当 时,
设
新课探究
yOz平面
追问2:能否用空间向量的坐标表示长度和夹角?
平面向量的长度和夹角
空间向量的长度和夹角
你能证明空间两点间的距离公式吗?
设 则
设
设
设 则
新课探究
你能证明空间两点间的距离公式吗?
设 , 是空间中任意两点,
如图,建立空间直角坐标系,
于是
所以
这就是空间两点间的距离公式.
则
应用新知
例1
应用新知
应用新知
反思感悟
1.在空间中根据点的坐标确定点的位置的方法
根据点的坐标确定点的位置,要先确定点(x0,y0)在Oxy平面上的位置,再由竖坐标确定点(x0,y0,z0)在空间直角坐标系中的位置.
(1)让尽可能多的点落在坐标轴上或坐标平面内;
(2)充分利用几何图形的特性.
一般先找出这一点在某一坐标平面上的射影,确定其两个坐标,再找出它在另一坐标轴上的射影(或者通过它到这个坐标平面的距离加上正号或负号),确定第三个坐标.
2.建立空间直角坐标系时应遵循的原则
3.求点的坐标的方法
应用新知
变式训练
详解
应用新知
例2
应用新知
O
A
B
C
x
y
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
z
例3
应用新知
O
A
B
C
x
y
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
z
应用新知
O
A
B
C
x
y
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
z
应用新知
规律方法
1.利用向量数量积的坐标公式求异面直线所成角的步骤
(1)根据几何图形的特点建立适当的空间直角坐标系;
(2)利用已知条件写出有关点的坐标,进而获得相关向量的坐标;
(3)利用向量数量积的坐标公式求得异面直线上有关向量的夹角,并将它转化为异面直线所成的角.
(1)建立适当的空间直角坐标系;
(2)求出线段端点的坐标;
(3)利用两点间的距离公式求出线段的长.
2.利用向量坐标求空间中线段的长度的一般步骤
应用新知
变式训练
能力提升
题型一
空间直角坐标系中的对称性问题
例题
能力提升
题型一
空间直角坐标系中的对称性问题
解析
应用新知
方法总结
yOz平面
求对称点的坐标可按以下规律写出:“关于谁对称谁不变,其余的符号均相反.”在空间直角坐标系中,任一点P(a,b,c)的几种特殊的对称点的坐标如下:
对称轴或对称中心
对称点坐标
坐标原点
x轴
y轴
z轴
xOy平面
yOz平面
xOz平面
(a,-b,-c)
(-a,b,-c)
(-a,-b,c)
(a,b,-c)
(-a,b,c)
(a,-b,c)
(-a,-b,-c)
P(a,b,c)
能力提升
方法总结
能力提升
题型一
空间直角坐标系中的对称性问题
变式训练
能力提升
题型一
空间直角坐标系中的对称性问题
解析
能力提升
题型二
空间向量的坐标运算
例题
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
应用新知
方法总结
进行空间向量的数量积坐标运算的技巧
应用新知
方法总结
应用新知
方法总结
判断空间向量垂直或平行的步骤
能力提升
题型二
空间向量的坐标运算
变式训练
解析
能力提升
题型二
空间向量的坐标运算
变式训练
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
课堂小结
yOz平面
空间向量及其运算的坐标表示
作业布置
巩固作业:教科书第21页练习第4、5题
教科书第22-23页习题第6、7、8题
作业答案
详解
作业答案
详解
作业答案
详解
作业答案
详解
作业答案
详解
第一章 空间向量与立体几何1.3 空间向量及其坐标运算
·选择性必修第一册·
1
学习目标
了解空间向量基本定理及其意义,掌握空间向量的正交分解及其坐标表示。
掌握空间向量的线性运算及其坐标表示。
掌握空间向量的数量积及其坐标表示。
2
3
(一)课程标准要求
1
学习目标
2
3
(二)课时目标要求
4
理解空间直角坐标系,感受建立空间直角坐标系的必要性.
借助空间直角坐标系理解空间中点的坐标和向量的坐标的概念及坐标表示.
会用坐标表示空间向量的线性运算及数量积运算.
会利用空间向量运算的坐标表示解决一些简单的立体几何问题.
引入新知
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点排除了数量关系……对于集合,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法……”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
引入新知
情境二
情境Ⅰ:如图,数轴上有A,B两点.
情境Ⅱ:在平面直角坐标系中,点P,Q的位置如图所示.
【思考】
(1)情境Ⅰ中如何表示A,B两点的位置
(2)情境Ⅱ中如何表示P,Q两点的位置
(3)对于情境Ⅲ,空间中如何表示板凳和气球的位置
情境Ⅲ:一个房间的示意图如图所示,我们如何表示板凳和气球的位置
新课探究
问题1
我们是如何建立平面向量的坐标表示的 你能类比平面直角坐标系与平面向量单位正交基的关系,你能利用空间向量单位正交基底概念构建空间直角坐标系吗
x
y
O
i
j
新课探究
新课探究
在空间直角坐标系中,让右手拇指指向 轴的正方向,食指指向 轴的正方向,如果中指指向 轴的正方向,则称这个坐标系为右手直角坐标系.
新课探究
问题2
在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢
x
y
O
i
j
A
a
新课探究
追问1:在空间直角坐标系中如何定义 的坐标呢?
x
y
O
i
j
a
A
平面直角坐标系内
空间直角坐标系内
取与 轴、 轴方向相同的两个单位向量 , 为基底,由平面向量基本定理,有且只有一对实数 , ,使得 . 我们把有序数对 , 叫做 的坐标,记作 , .
取与 轴、 轴、 轴方向相同的单位向量 , , 为基底,由空间向量基本定理,存在唯一的有序实数组 , , ,使得
新课探究
定义:在单位正交基底 , , 下与向量 对应的有序实数组 , , ,叫做点 在空间直角坐标系中的坐标,记作 , , , 其中 叫做点 的横坐标, 叫做点 的纵坐标, 叫做点 的竖坐标.
新课探究
追问2:对于给定的向量 又该如何定义它的坐标呢?
我们在空间直角坐标系 中可以作 .
由空间向量基本定理,存在唯一的有序实数组 , , ,使
有序实数组 , , 叫做 在空间直角坐标系 中的坐标,上式可简记为 , ,
新课探究
问题3
在空间直角坐标系 中,对空间任意一点 ,或任意一个向量 ,你能借助几何直观确定它们的坐标 , , 吗?
过点 分别作垂直于 轴、 轴和 轴的平面
依次交 轴、 轴和 轴于点 , 和 .
即点 或者向量 的
坐标就是 , , .
可以证明 在 轴、 轴、 轴上的投影向量分别为 , , .
新课探究
问题4
有了空间向量的坐标表示,你能类比平面向量的坐标运算,得出空间向量运算的坐标表示并给出证明吗 请同学们类比平面向量运算的坐标表示研究空间向量运算的坐标表示,独立完成下列表格,并进行小组交流
新课探究
设
设
设
设
加法运算
减法运算
平面向量坐标运算
空间向量坐标运算
数乘运算
数量积运算
有向线段的向量坐标表示
线性运算
新课探究
下面我们证明空间向量数量积运算的坐标表示.
请同学们证明剩下运算的坐标表示
设 为空间的一个单位正交基底,
则
所以
因为
所以
新课探究
问题5
平面向量的坐标运算可以帮助我们解决平行、垂直等位置关系以及距离,角度等度量问题.空间向量的坐标运算是否仍然可以帮助我们解决这些问题?
新课探究
yOz平面
追问1:如何用平面向量的坐标运算刻画平面向量的平行和垂直?
平面向量的特殊位置关系
平面向量的特殊位置关系
设
当 时,
当 时,
设
能否表示为 ?
新课探究
当 时,
设
能否表示为 ?
至少一个不为0.
例如:当 与平面 平行时, .此时 无意义.
例如:当 与平面 平行时, .此时 无意义.
因此,只有 均不为0时,
特殊地, 与任意向量平行.
当 时,
新课探究
yOz平面
平面向量的特殊位置关系
空间向量的特殊位置关系
设
当 时,
当 时,
设
新课探究
yOz平面
追问2:能否用空间向量的坐标表示长度和夹角?
平面向量的长度和夹角
空间向量的长度和夹角
你能证明空间两点间的距离公式吗?
设 则
设
设
设 则
新课探究
你能证明空间两点间的距离公式吗?
设 , 是空间中任意两点,
如图,建立空间直角坐标系,
于是
所以
这就是空间两点间的距离公式.
则
应用新知
例1
应用新知
应用新知
反思感悟
1.在空间中根据点的坐标确定点的位置的方法
根据点的坐标确定点的位置,要先确定点(x0,y0)在Oxy平面上的位置,再由竖坐标确定点(x0,y0,z0)在空间直角坐标系中的位置.
(1)让尽可能多的点落在坐标轴上或坐标平面内;
(2)充分利用几何图形的特性.
一般先找出这一点在某一坐标平面上的射影,确定其两个坐标,再找出它在另一坐标轴上的射影(或者通过它到这个坐标平面的距离加上正号或负号),确定第三个坐标.
2.建立空间直角坐标系时应遵循的原则
3.求点的坐标的方法
应用新知
变式训练
详解
应用新知
例2
应用新知
O
A
B
C
x
y
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
z
例3
应用新知
O
A
B
C
x
y
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
z
应用新知
O
A
B
C
x
y
图1.3-9
D
A1
B1
C1
D1
F1
M
E1
z
应用新知
规律方法
1.利用向量数量积的坐标公式求异面直线所成角的步骤
(1)根据几何图形的特点建立适当的空间直角坐标系;
(2)利用已知条件写出有关点的坐标,进而获得相关向量的坐标;
(3)利用向量数量积的坐标公式求得异面直线上有关向量的夹角,并将它转化为异面直线所成的角.
(1)建立适当的空间直角坐标系;
(2)求出线段端点的坐标;
(3)利用两点间的距离公式求出线段的长.
2.利用向量坐标求空间中线段的长度的一般步骤
应用新知
变式训练
能力提升
题型一
空间直角坐标系中的对称性问题
例题
能力提升
题型一
空间直角坐标系中的对称性问题
解析
应用新知
方法总结
yOz平面
求对称点的坐标可按以下规律写出:“关于谁对称谁不变,其余的符号均相反.”在空间直角坐标系中,任一点P(a,b,c)的几种特殊的对称点的坐标如下:
对称轴或对称中心
对称点坐标
坐标原点
x轴
y轴
z轴
xOy平面
yOz平面
xOz平面
(a,-b,-c)
(-a,b,-c)
(-a,-b,c)
(a,b,-c)
(-a,b,c)
(a,-b,c)
(-a,-b,-c)
P(a,b,c)
能力提升
方法总结
能力提升
题型一
空间直角坐标系中的对称性问题
变式训练
能力提升
题型一
空间直角坐标系中的对称性问题
解析
能力提升
题型二
空间向量的坐标运算
例题
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
应用新知
方法总结
进行空间向量的数量积坐标运算的技巧
应用新知
方法总结
应用新知
方法总结
判断空间向量垂直或平行的步骤
能力提升
题型二
空间向量的坐标运算
变式训练
解析
能力提升
题型二
空间向量的坐标运算
变式训练
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
能力提升
题型二
空间向量的坐标运算
解析
课堂小结
yOz平面
空间向量及其运算的坐标表示
作业布置
巩固作业:教科书第21页练习第4、5题
教科书第22-23页习题第6、7、8题
作业答案
详解
作业答案
详解
作业答案
详解
作业答案
详解
作业答案
详解
