人教A版高中数学选择性必修第一册1.1.2空间向量的数量积运算 课件(共40张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.1.2空间向量的数量积运算 课件(共40张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:36:55 | ||
图片预览








文档简介
(共40张PPT)
·选择性必修第一册·
1
学习目标
掌握空间向量的夹角的概念,培养数学抽象的核心素养.
掌握空间向量的数量积的定义、性质、运算律,提升数学抽象的核心素养.
了解空间向量投影的概念以及投影向量的意义,培养直观想象的核心素养.
能用空间向量的数量积解决立体几何中的垂直、夹角、长度等问题,强化数学运算的核心素养.
2
3
4
引入新知
G20峰会向世界展示了杭州的无穷魅力,一些别致的建筑和设计令人印象深刻!设计、制造这些宏伟的建筑、精美的造型,都会遇到许多立体几何问题,比如建筑的地面垂不垂直,要不要垂直 构成建筑的部件长度是多少 彼此成多少角度比较合适等等.怎么样才能解决这些问题呢,必须有强大的数学工具!
学习新知
追问:空间向量有数量积吗 为什么 是怎样的
问题2:我们已经学面向量,并深刻地体会到平面向量在解决垂直、长度、角度等问题中的应用.我们还学习了空间向量的加法、减法、数乘运算,那么空间向量中,怎么样的运算能支持判断垂直问题,计算长度、角度问题
问题1:在所学的数学工具中,哪些可以用来研究垂直问题,计算长度、角度问题
追问(1):学习平面向量时,我们是如何研究它的数量积运算的?
问题3:我们已经学面向量的数量积运算,你能类比平面向量,给出空间向量的数量积运算的定义吗?
夹角
数量积的定义
运算律
应用
学习新知
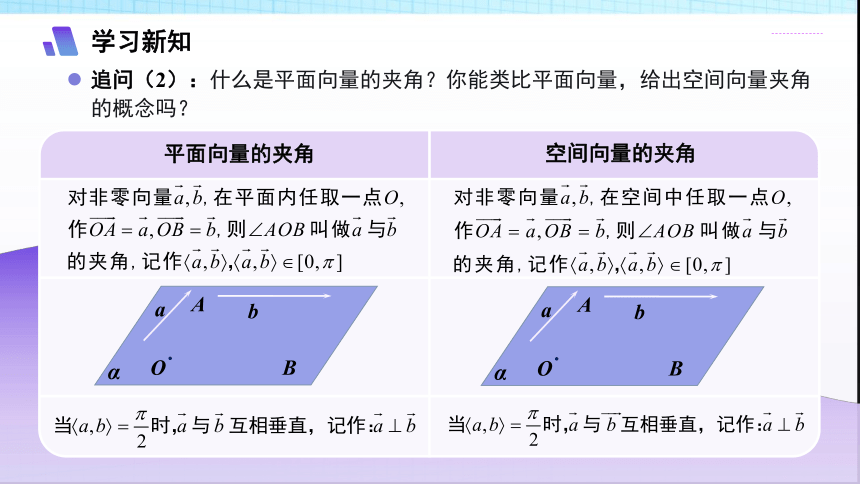
追问(2):什么是平面向量的夹角?你能类比平面向量,给出空间向量夹角的概念吗?
平面向量的夹角
空间向量的夹角
b
a
.
O
B
α
A
b
a
.
O
B
α
A
学习新知
追问(3):平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
平面向量的数量积
空间向量的数量积
证明垂直关系
求线段长度
求夹角大小
学习新知
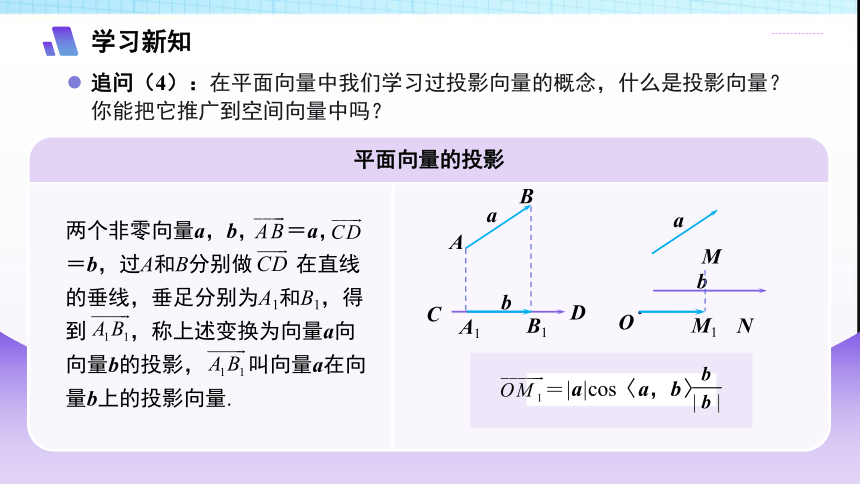
追问(4):在平面向量中我们学习过投影向量的概念,什么是投影向量?你能把它推广到空间向量中吗?
平面向量的投影
两个非零向量a,b, =a, =b,过A和B分别做 在直线的垂线,垂足分别为A1和B1,得到 ,称上述变换为向量a向向量b的投影, 叫向量a在向量b上的投影向量.
=|a|cos〈a,b〉
b
a
A
B
D
C
A1
B1
b
a
.
O
N
M
M1
学习新知
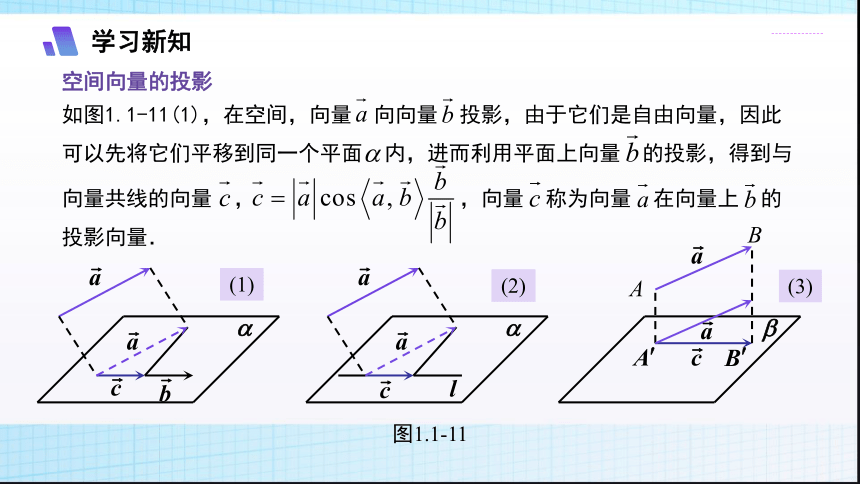
空间向量的投影
如图1.1-11(1),在空间,向量 向向量 投影,由于它们是自由向量,因此可以先将它们平移到同一个平面 内,进而利用平面上向量 的投影,得到与
向量共线的向量 , ,向量 称为向量 在向量上 的投影向量.
A
B
(1)
(2)
(3)
图1.1-11
学习新知
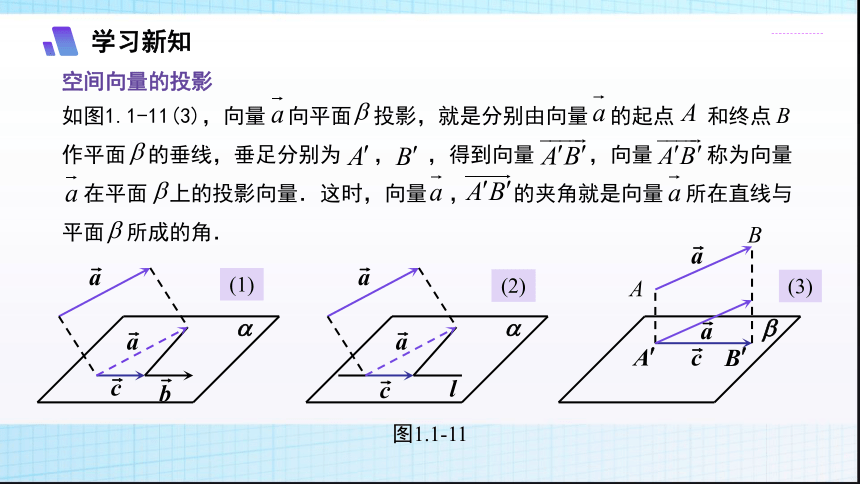
如图1.1-11(3),向量 向平面 投影,就是分别由向量 的起点 和终点 作平面 的垂线,垂足分别为 , ,得到向量 ,向量 称为向量
在平面 上的投影向量.这时,向量 , 的夹角就是向量 所在直线与平面 所成的角.
A
B
(1)
(2)
(3)
图1.1-11
空间向量的投影
学习新知
追问(5):类比平面向量数量积运算的运算律,空间向量的数量积运算有哪些运算律?如何证明?
空间向量的数量积满足如下的运算律:
(交换律);
, ;
(分配律).
请同学们课后给出运算律的证明
学习新知
1.对于三个均不为0的数 ,若 ,则 .对于向量 , , ,由 ,你能得到 吗?如果不能,请举出反例.
设 是非零向量,且 ,求证:
O
B
C
A
思考
学习新知
思考
2. 对于三个均不为0的数 ,若 ,则 (或 ).对于向量
, ,若 ,能不能写成 (或 )的形式?
3. 对三个不为0的数 ,有 ,对于向量 , , ,
成立吗?为什么
2. 不能!因为没有定义向量的除法运算.
3. 不一定!两个向量的数量积为一个实数,(a·b)c 和 a(b·c) 分别表示与向量c和向量a共线的向量,它们不一定相等.向量的数量积运算没有结合律.
应用新知
A
B
C
D
应用新知
A
B
C
D
应用新知
规律方法
(1)已知向量的模和夹角
利用 并结合运算律进行计算.
(2)在几何体中求空间向量的数量积
先将各向量分解成已知模和夹角的向量的组合形式.再利用向量的运算律将数量积展开,转化成已知模和夹角的向量的数量积.
应用新知
如图,连接AG并延长,与BC交于点D,连接OG,
∵点G是底面△ABC的重心,
应用新知
应用新知
l
m
n
g
分析
应用新知
l
m
n
g
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
M
能力提升
题型一
空间向量数量积的运算
例题
M
应用新知
方法总结
利用定义,直接利用a·b=|a||b|cos并结合运算律进行计算.
利用图形,计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.
利用向量分解,在几何体中进行向量的数量积运算时,要充分利用几何体的性质,把待求向量用已知夹角和模的向量表示后再进行运算.
步骤:(1)首先将各向量分解成已知模和夹角的向量的线性组合形式;
利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积;
代入a·b=|a||b|cos求解.
能力提升
题型二
利用数量积求解距离,角度等几何元素
例题
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
应用新知
方法总结
应用新知
方法总结
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
应用新知
规律方法
(1)证明线线垂直的方法:证明线线垂直的关键是确定直线的方向向量,看方向向量的数量积是否为0来判断两直线是否垂直.
(2)证明与空间向量a,b,c有关的向量m,n垂直的方法:先用向量a,b,c表示向量m,n,再求解向量m,n的数量积判断是否垂直.
课堂小结
作业布置
巩固作业:教科书第10页习题第8,10题。
拓展作业:证明空间向量数量积的运算律。
作业答案
8. 用向量方法证明:在平面内的一条直线,如果与这个平面的一条斜线在这个平面上的射影垂直,那么它也与这条斜线垂直(三垂线定理).
作业答案
作业答案
·选择性必修第一册·
1
学习目标
掌握空间向量的夹角的概念,培养数学抽象的核心素养.
掌握空间向量的数量积的定义、性质、运算律,提升数学抽象的核心素养.
了解空间向量投影的概念以及投影向量的意义,培养直观想象的核心素养.
能用空间向量的数量积解决立体几何中的垂直、夹角、长度等问题,强化数学运算的核心素养.
2
3
4
引入新知
G20峰会向世界展示了杭州的无穷魅力,一些别致的建筑和设计令人印象深刻!设计、制造这些宏伟的建筑、精美的造型,都会遇到许多立体几何问题,比如建筑的地面垂不垂直,要不要垂直 构成建筑的部件长度是多少 彼此成多少角度比较合适等等.怎么样才能解决这些问题呢,必须有强大的数学工具!
学习新知
追问:空间向量有数量积吗 为什么 是怎样的
问题2:我们已经学面向量,并深刻地体会到平面向量在解决垂直、长度、角度等问题中的应用.我们还学习了空间向量的加法、减法、数乘运算,那么空间向量中,怎么样的运算能支持判断垂直问题,计算长度、角度问题
问题1:在所学的数学工具中,哪些可以用来研究垂直问题,计算长度、角度问题
追问(1):学习平面向量时,我们是如何研究它的数量积运算的?
问题3:我们已经学面向量的数量积运算,你能类比平面向量,给出空间向量的数量积运算的定义吗?
夹角
数量积的定义
运算律
应用
学习新知
追问(2):什么是平面向量的夹角?你能类比平面向量,给出空间向量夹角的概念吗?
平面向量的夹角
空间向量的夹角
b
a
.
O
B
α
A
b
a
.
O
B
α
A
学习新知
追问(3):平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
平面向量的数量积
空间向量的数量积
证明垂直关系
求线段长度
求夹角大小
学习新知
追问(4):在平面向量中我们学习过投影向量的概念,什么是投影向量?你能把它推广到空间向量中吗?
平面向量的投影
两个非零向量a,b, =a, =b,过A和B分别做 在直线的垂线,垂足分别为A1和B1,得到 ,称上述变换为向量a向向量b的投影, 叫向量a在向量b上的投影向量.
=|a|cos〈a,b〉
b
a
A
B
D
C
A1
B1
b
a
.
O
N
M
M1
学习新知
空间向量的投影
如图1.1-11(1),在空间,向量 向向量 投影,由于它们是自由向量,因此可以先将它们平移到同一个平面 内,进而利用平面上向量 的投影,得到与
向量共线的向量 , ,向量 称为向量 在向量上 的投影向量.
A
B
(1)
(2)
(3)
图1.1-11
学习新知
如图1.1-11(3),向量 向平面 投影,就是分别由向量 的起点 和终点 作平面 的垂线,垂足分别为 , ,得到向量 ,向量 称为向量
在平面 上的投影向量.这时,向量 , 的夹角就是向量 所在直线与平面 所成的角.
A
B
(1)
(2)
(3)
图1.1-11
空间向量的投影
学习新知
追问(5):类比平面向量数量积运算的运算律,空间向量的数量积运算有哪些运算律?如何证明?
空间向量的数量积满足如下的运算律:
(交换律);
, ;
(分配律).
请同学们课后给出运算律的证明
学习新知
1.对于三个均不为0的数 ,若 ,则 .对于向量 , , ,由 ,你能得到 吗?如果不能,请举出反例.
设 是非零向量,且 ,求证:
O
B
C
A
思考
学习新知
思考
2. 对于三个均不为0的数 ,若 ,则 (或 ).对于向量
, ,若 ,能不能写成 (或 )的形式?
3. 对三个不为0的数 ,有 ,对于向量 , , ,
成立吗?为什么
2. 不能!因为没有定义向量的除法运算.
3. 不一定!两个向量的数量积为一个实数,(a·b)c 和 a(b·c) 分别表示与向量c和向量a共线的向量,它们不一定相等.向量的数量积运算没有结合律.
应用新知
A
B
C
D
应用新知
A
B
C
D
应用新知
规律方法
(1)已知向量的模和夹角
利用 并结合运算律进行计算.
(2)在几何体中求空间向量的数量积
先将各向量分解成已知模和夹角的向量的组合形式.再利用向量的运算律将数量积展开,转化成已知模和夹角的向量的数量积.
应用新知
如图,连接AG并延长,与BC交于点D,连接OG,
∵点G是底面△ABC的重心,
应用新知
应用新知
l
m
n
g
分析
应用新知
l
m
n
g
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
能力提升
题型一
空间向量数量积的运算
例题
M
能力提升
题型一
空间向量数量积的运算
例题
M
应用新知
方法总结
利用定义,直接利用a·b=|a||b|cos
利用图形,计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.
利用向量分解,在几何体中进行向量的数量积运算时,要充分利用几何体的性质,把待求向量用已知夹角和模的向量表示后再进行运算.
步骤:(1)首先将各向量分解成已知模和夹角的向量的线性组合形式;
利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积;
代入a·b=|a||b|cos
能力提升
题型二
利用数量积求解距离,角度等几何元素
例题
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
应用新知
方法总结
应用新知
方法总结
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
能力提升
例题
题型二
利用数量积求解距离,角度等几何元素
应用新知
规律方法
(1)证明线线垂直的方法:证明线线垂直的关键是确定直线的方向向量,看方向向量的数量积是否为0来判断两直线是否垂直.
(2)证明与空间向量a,b,c有关的向量m,n垂直的方法:先用向量a,b,c表示向量m,n,再求解向量m,n的数量积判断是否垂直.
课堂小结
作业布置
巩固作业:教科书第10页习题第8,10题。
拓展作业:证明空间向量数量积的运算律。
作业答案
8. 用向量方法证明:在平面内的一条直线,如果与这个平面的一条斜线在这个平面上的射影垂直,那么它也与这条斜线垂直(三垂线定理).
作业答案
作业答案
