人教A版高中数学选择性必修第一册1.4.1用空间向量研究空间中直线、平面的平行(第2课时) 课件(共52张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.1用空间向量研究空间中直线、平面的平行(第2课时) 课件(共52张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:37:16 | ||
图片预览






文档简介
(共52张PPT)
·选择性必修第一册·
第2课时 空间中直线、平面的平行
1
学习目标
一、课程标准要求:
能用向量语言表述直线与直线、直线与平面、平面与平面的夹角以
及垂直与平行关系.
能用向量方法证明必修内容中有关直线、平面位置关系的判定定理.
2
1
学习目标
二、课时目标要求:
能用向量的语言表述线线、线面、面面的平行关系,积累直观想象
经验.
能用向量的方法证明空间线面平行的有关定理.
能用向量的方法判断并证明空间中的直线、平面平行关系,提升逻
辑推理和数学运算素养.
2
3
引入新知
情景一:牌楼与牌坊类似,是中国传统建筑之一,最早见于周朝.在园林、寺观、宫苑、陵墓和街道常有建造.旧时牌楼主要有木、石、木石、砖木、琉璃几种,多设于要道口.牌楼中有一种有柱门形构筑物,一般较高大.如图,牌楼的柱子与地面是垂直的,如果牌楼上部的下边线与柱子垂直,我们就能知道下边线与地面平行.这是为什么呢?
引入新知
情景二:在天安门广场看到,解放军仪仗队、军乐团以“亮相即精彩、出场即震撼”的标准,高质量完成每天的升旗任务,充分展示了全党全军全国人民奋进新时代、开启新征程的时代风貌。观察图片,旗杆底部的平台和地面平行,旗杆所在的直线和护旗战士所在的直线平行.旗杆所在直线的方向向量和护旗战士所在直线的方向向量有什么关系?
新课探究
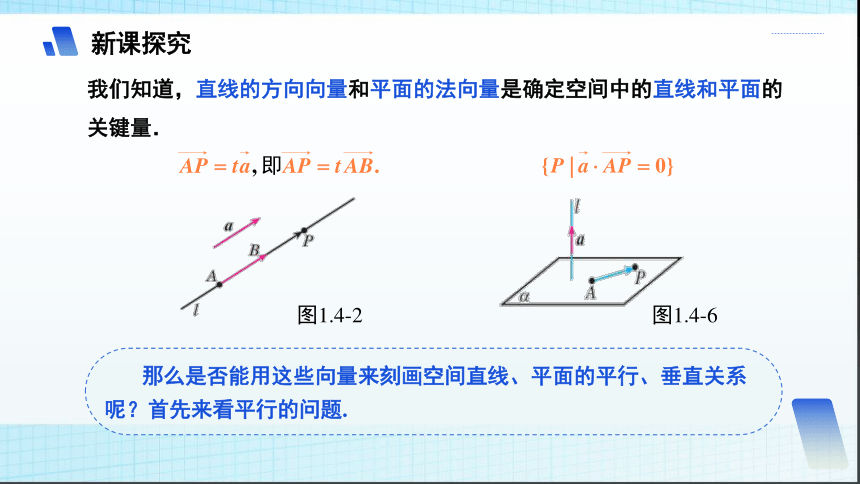
我们知道,直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量.
那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢?首先来看平行的问题.
图1.4-2
图1.4-6
新课探究
问题1: 由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系 反过来,由直线的方向向量、平面的法向量之间的平行关系,可以得到直线、平面的什么关系
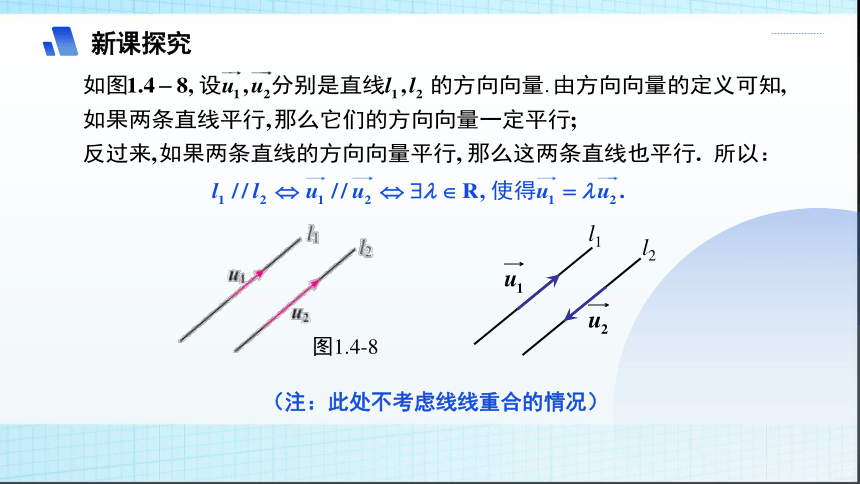
新课探究
l1
l2
(注:此处不考虑线线重合的情况)
图1.4-8
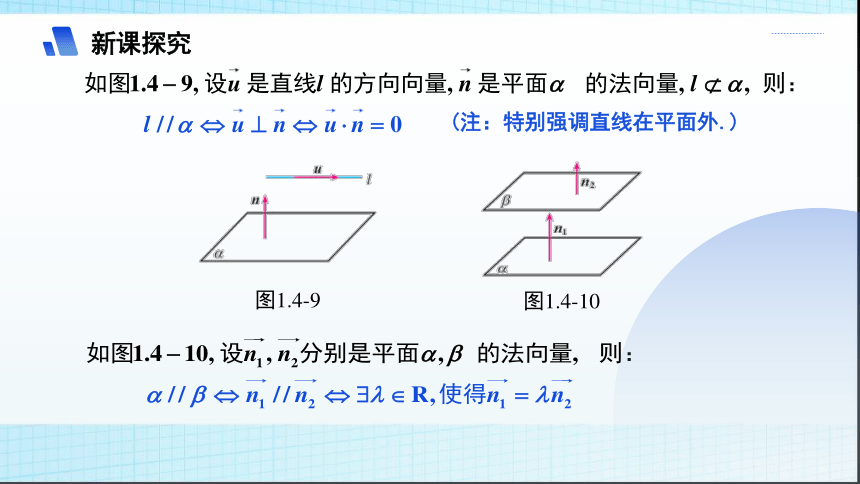
新课探究
图1.4-9
图1.4-10
(注:特别强调直线在平面外.)
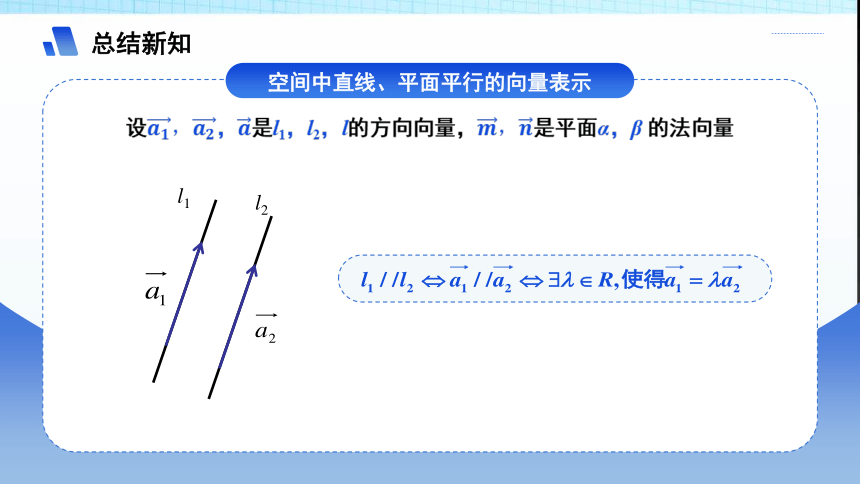
总结新知
空间中直线、平面平行的向量表示
l1
l2
总结新知
空间中直线、平面平行的向量表示
l
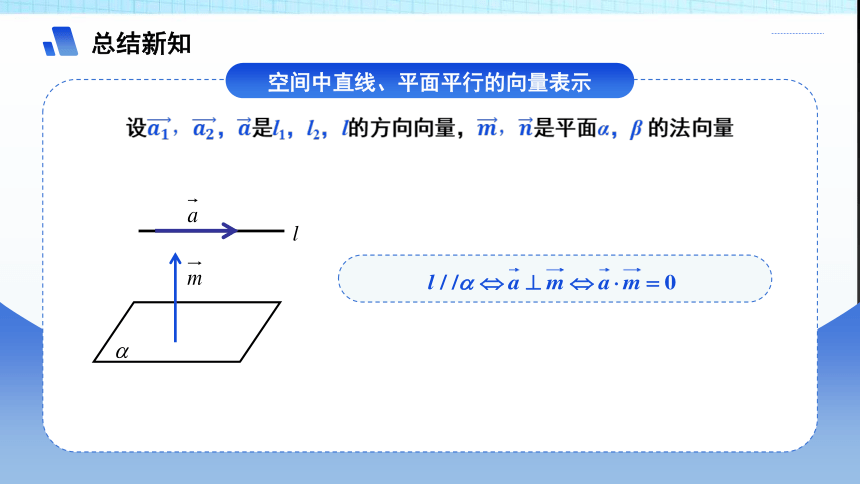
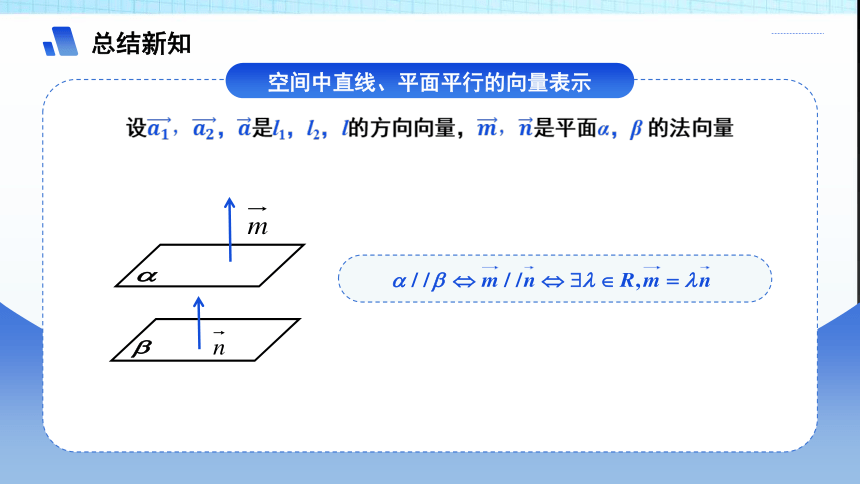
总结新知
空间中直线、平面平行的向量表示
应用新知
应用新知
应用新知
规律小结
证明空间两直线平行的思路
(1)把证明空间两直线平行的问题转化为判断空间两直线的方向向量共线;
(2)在建立空间直角坐标系后,主要问题是求出空间两直线的方向向量的坐标.
应用新知
规律小结
利用空间向量证明线线平行的方法步骤
(1)建立适当的空间直角坐标系,求出相应点的坐标.
(2)求出直线的方向向量.
(3)证明两向量共线.
(4)证明其中一个向量所在直线上的一点不在另一个向量所在的直线上,即表示方向向量的有向线段不共线,从而得证.
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
应用新知
图1.4-11
例2: 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
分析:
应用新知
图1.4-11
例2: 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
证明:
应用新知
方法规律
空间向量证明两个平面平行的思路方法
(1)直接证明法:建立空间直角坐标系,分别求出两个平面的法向量,证明两个法向量平行.
(2)转化的思路:根据两个平面平行的判定定理,把证明两个平面平行转化为证明线面平行或线线平行,再利用空间向量证明.
应用新知
变式训练:
应用新知
变式训练:
方法一:
应用新知
变式训练:
方法一:
应用新知
变式训练:
方法二:
应用新知
变式训练:
方法二:
应用新知
变式训练:
方法二:
应用新知
分析:
应用新知
应用新知
规律小结
利用空间向量证明线面平行的方法
方法一:证明直线的方向向量与平面内任意两个不共线的向量共面,即可用平面内的一组基底表示.
方法二:证明直线的方向向量与平面内某一向量共线,转化为线线平行,利用线面平行判定定理得证.
方法三:先求直线的方向向量,再求平面的法向量,证明直线的方向向量与平面的法向量垂直.
应用新知
3.用向量方法证明“直线与平面平行的判定定理”:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
变式训练:
l
m
证明:
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
图1.4-12
分析
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
应用新知
方法总结
存在型问题与探究型问题的求解方法
1.对于存在判断型问题的求解,应先假设存在,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.
2.对于位置探究型问题,通常借助向量,引进参数,综合已知和结论列出等式,解出参数.
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
此方程组无解
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
课堂小结
作业布置
巩固作业:教科书第42-44页习题1.4第3、4、12题.
作业答案(教科书第42页习题1.4第3题)
证明
作业答案(教科书第42页习题1.4第4题)
证明
作业答案(教科书第42页习题1.4第4题)
证明
作业答案(教科书第44页习题1.4第12题)
证明
作业答案(教科书第44页习题1.4第12题)
证明
·选择性必修第一册·
第2课时 空间中直线、平面的平行
1
学习目标
一、课程标准要求:
能用向量语言表述直线与直线、直线与平面、平面与平面的夹角以
及垂直与平行关系.
能用向量方法证明必修内容中有关直线、平面位置关系的判定定理.
2
1
学习目标
二、课时目标要求:
能用向量的语言表述线线、线面、面面的平行关系,积累直观想象
经验.
能用向量的方法证明空间线面平行的有关定理.
能用向量的方法判断并证明空间中的直线、平面平行关系,提升逻
辑推理和数学运算素养.
2
3
引入新知
情景一:牌楼与牌坊类似,是中国传统建筑之一,最早见于周朝.在园林、寺观、宫苑、陵墓和街道常有建造.旧时牌楼主要有木、石、木石、砖木、琉璃几种,多设于要道口.牌楼中有一种有柱门形构筑物,一般较高大.如图,牌楼的柱子与地面是垂直的,如果牌楼上部的下边线与柱子垂直,我们就能知道下边线与地面平行.这是为什么呢?
引入新知
情景二:在天安门广场看到,解放军仪仗队、军乐团以“亮相即精彩、出场即震撼”的标准,高质量完成每天的升旗任务,充分展示了全党全军全国人民奋进新时代、开启新征程的时代风貌。观察图片,旗杆底部的平台和地面平行,旗杆所在的直线和护旗战士所在的直线平行.旗杆所在直线的方向向量和护旗战士所在直线的方向向量有什么关系?
新课探究
我们知道,直线的方向向量和平面的法向量是确定空间中的直线和平面的关键量.
那么是否能用这些向量来刻画空间直线、平面的平行、垂直关系呢?首先来看平行的问题.
图1.4-2
图1.4-6
新课探究
问题1: 由直线与直线、直线与平面或平面与平面的平行关系,可以得到直线的方向向量、平面的法向量间的什么关系 反过来,由直线的方向向量、平面的法向量之间的平行关系,可以得到直线、平面的什么关系
新课探究
l1
l2
(注:此处不考虑线线重合的情况)
图1.4-8
新课探究
图1.4-9
图1.4-10
(注:特别强调直线在平面外.)
总结新知
空间中直线、平面平行的向量表示
l1
l2
总结新知
空间中直线、平面平行的向量表示
l
总结新知
空间中直线、平面平行的向量表示
应用新知
应用新知
应用新知
规律小结
证明空间两直线平行的思路
(1)把证明空间两直线平行的问题转化为判断空间两直线的方向向量共线;
(2)在建立空间直角坐标系后,主要问题是求出空间两直线的方向向量的坐标.
应用新知
规律小结
利用空间向量证明线线平行的方法步骤
(1)建立适当的空间直角坐标系,求出相应点的坐标.
(2)求出直线的方向向量.
(3)证明两向量共线.
(4)证明其中一个向量所在直线上的一点不在另一个向量所在的直线上,即表示方向向量的有向线段不共线,从而得证.
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
应用新知
图1.4-11
例2: 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
分析:
应用新知
图1.4-11
例2: 证明“平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
证明:
应用新知
方法规律
空间向量证明两个平面平行的思路方法
(1)直接证明法:建立空间直角坐标系,分别求出两个平面的法向量,证明两个法向量平行.
(2)转化的思路:根据两个平面平行的判定定理,把证明两个平面平行转化为证明线面平行或线线平行,再利用空间向量证明.
应用新知
变式训练:
应用新知
变式训练:
方法一:
应用新知
变式训练:
方法一:
应用新知
变式训练:
方法二:
应用新知
变式训练:
方法二:
应用新知
变式训练:
方法二:
应用新知
分析:
应用新知
应用新知
规律小结
利用空间向量证明线面平行的方法
方法一:证明直线的方向向量与平面内任意两个不共线的向量共面,即可用平面内的一组基底表示.
方法二:证明直线的方向向量与平面内某一向量共线,转化为线线平行,利用线面平行判定定理得证.
方法三:先求直线的方向向量,再求平面的法向量,证明直线的方向向量与平面的法向量垂直.
应用新知
3.用向量方法证明“直线与平面平行的判定定理”:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
变式训练:
l
m
证明:
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
图1.4-12
分析
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
能力提升
例题
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
图1.4-12
应用新知
方法总结
存在型问题与探究型问题的求解方法
1.对于存在判断型问题的求解,应先假设存在,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等.
2.对于位置探究型问题,通常借助向量,引进参数,综合已知和结论列出等式,解出参数.
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
此方程组无解
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面平行的探究性问题.
解析
课堂小结
作业布置
巩固作业:教科书第42-44页习题1.4第3、4、12题.
作业答案(教科书第42页习题1.4第3题)
证明
作业答案(教科书第42页习题1.4第4题)
证明
作业答案(教科书第42页习题1.4第4题)
证明
作业答案(教科书第44页习题1.4第12题)
证明
作业答案(教科书第44页习题1.4第12题)
证明
