人教A版高中数学选择性必修第一册1.4.1用空间向量研究空间中直线、平面的垂直(第3课时) 课件(共60张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.1用空间向量研究空间中直线、平面的垂直(第3课时) 课件(共60张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:37:48 | ||
图片预览








文档简介
(共60张PPT)
·选择性必修第一册·
第3课时 空间中直线、平面的垂直
1
学习目标
一、课程标准要求:
能用向量语言表述直线与直线、直线与平面、平面与平面的夹角以及
垂直与平行关系.
能用向量方法证明必修内容中有关直线、平面位置关系的判定定理.
2
1
学习目标
二、课时目标要求:
能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系,
发展数学抽象素养.
能用向量方法证明必修内容中有关直线、平面垂直关系的判定定理,
培养逻辑推理素养.
能用向量方法证明空间中直线、平面的垂直关系,培养逻辑推理素养.
2
3
引入新知
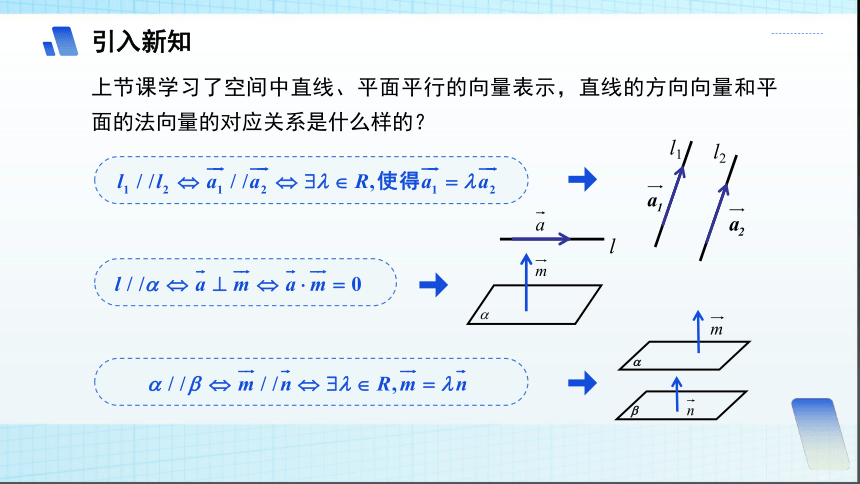
上节课学习了空间中直线、平面平行的向量表示,直线的方向向量和平面的法向量的对应关系是什么样的?
l1
l2
l
新课探究
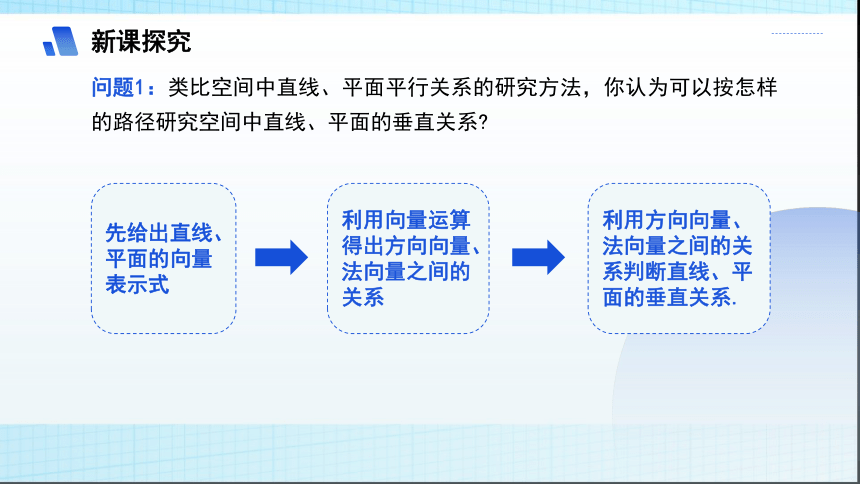
问题1:类比空间中直线、平面平行关系的研究方法,你认为可以按怎样的路径研究空间中直线、平面的垂直关系
先给出直线、平面的向量表示式
利用向量运算得出方向向量、法向量之间的关系
利用方向向量、法向量之间的关系判断直线、平面的垂直关系.
新课探究
问题2:类比空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系
一般地,直线与直线垂直,就是两直线的方向向量垂直;
直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
新课探究
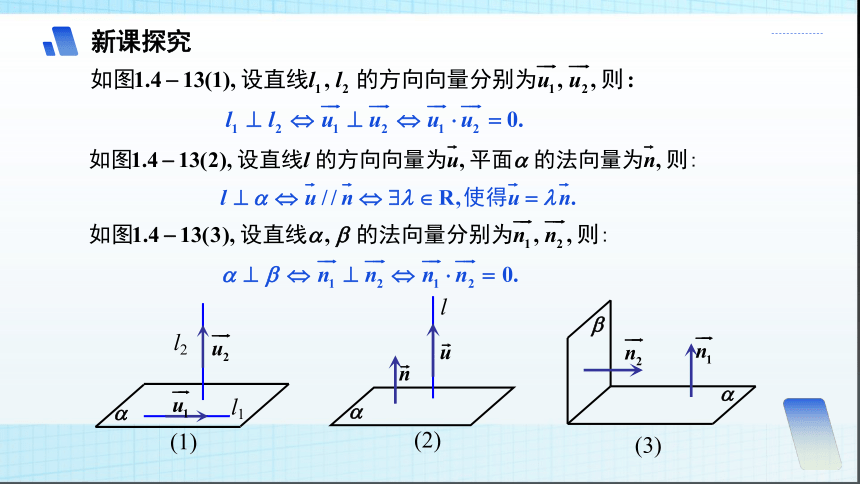
l1
l2
(1)
l
(2)
(3)
新课探究
思考:我们随时随地看到向量运算的作用,你同意“向量是躯体,运算是灵魂”“没有运算的向量只能起路标的作用”的说法吗?
有了向量的运算才能研究空间图形的位置关系、度量问题.向量的作用是通过其运算来体现的,如果没有运算,那么向量仅能表示空间中的点、直线和平面,只是“路标”,无法获得空间图形的几何性质.
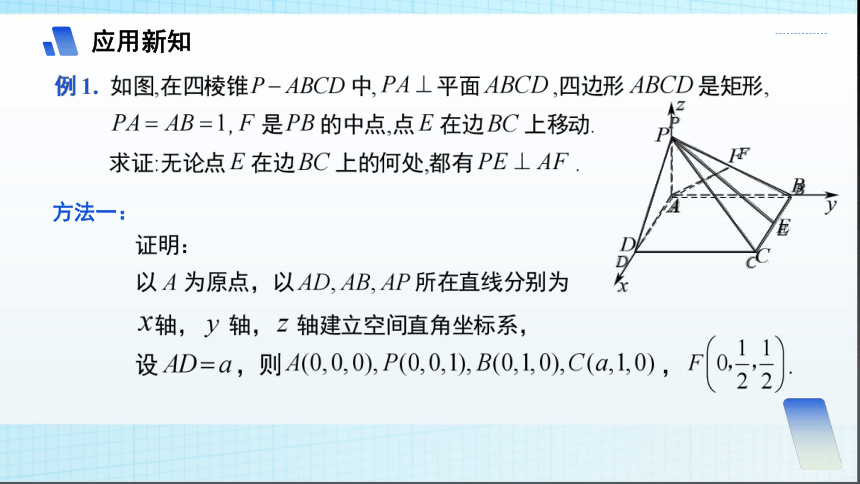
应用新知
分析:
应用新知
方法一:
应用新知
方法一:
应用新知
方法二:
应用新知
方法二:
应用新知
反思感悟
利用向量方法证明线线垂直的方法——基向量法:
①取三个不共线的已知向量(通常是它们的模及其两两夹角为已知)为空间的一个基底;
②用基底把两直线的方向向量表示出来;
③利用向量的数量积计算出两直线的方向向量的数量积为0;
④由方向向量垂直得到两直线垂直.
应用新知
反思感悟
利用向量方法证明线线垂直的方法——坐标法:
①根据已知条件和图形特征,建立适当的空间直角坐标系,正确地写出各点的坐标;
②根据所求出的点的坐标求出两直线方向向量的坐标;
③计算两直线方向向量的数量积为0;
④由方向向量垂直得到两直线垂直.
应用新知
变式训练:
应用新知
变式训练:
应用新知
应用新知
方法一
应用新知
方法一
应用新知
方法二
应用新知
方法二
应用新知
方法三
应用新知
方法三
应用新知
反思感悟
利用空间向量证明线面垂直的方法——基向量法:
①确定基向量作为空间的一个基底,用基向量表示有关直线的方向向量;
②找出平面内两条相交直线的方向向量,并分别用基向量表示;
③分别计算有关直线的方向向量与平面内相交直线的向量的数量积,根据数量积为0,证得线线垂直,然后由线面垂直的判定定理得出结论.
应用新知
反思感悟
利用空间向量证明线面垂直的方法——坐标法:
方法一:
①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③找出平面内两条相交直线,并用坐标表示它们的方向向量;
④分别计算两组向量的数量积,得到数量积为0,证得线线垂直,然后得出线面垂直.
应用新知
反思感悟
利用空间向量证明线面垂直的方法——坐标法:
方法二:
①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③求出平面的法向量;
④证明直线的方向向量与平面的法向量平行,得出线面垂直
应用新知
变式训练:
图1.4-14
应用新知
变式训练:
图1.4-14
应用新知
变式训练:
图1.4-14
应用新知
变式训练:
图1.4-14
应用新知
例3:证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,
则这两个平面垂直.
图1.4-15
分析:
证明:
应用新知
规律方法
利用空间向量证明线面垂直的方法
1.利用空间向量证明面面垂直的方法
(1)利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直,进而转化为线线垂直问题;
(2)直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直.
2.向量法证明面面垂直的优越性
主要体现在不必考虑图形的位置关系,恰当建系或用基向量表示后,只需经过向量运算就可得到要证明的结果,思路方法很“公式化”.
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
能力提升
例题
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
应用新知
方法总结
应用空间向量解答探索性(存在性)问题
立体几何中的存在探究题,解决思路一般有两个:
(1)根据题目的已知条件进行综合分析和观察猜想,找出点或线的位置,并用向量表示出来,然后再加以证明,得出结论;
(2)假设所求的点或参数存在,并用相关参数表示相关点,根据线、面满足的垂直、平行关系,构建方程(组)求解,若能求出参数的值且符合该限定的范围,则存在,否则不存在.
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
分析
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
分析
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
课堂小结
作业布置
巩固作业:教科书第33页练习第1题
教科书第42-43页习题1.4第5、8、11题
作业答案(教科书第33页练习第1题)
详解
作业答案(教科书第42-43页习题1.4第5题)
详解
作业答案(教科书第42-43页习题1.4第5题)
详解
作业答案(教科书第42-43页习题1.4第8题)
详解
作业答案(教科书第42-43页习题1.4第8题)
详解
作业答案(教科书第42-43页习题1.4第11题)
详解
作业答案(教科书第42-43页习题1.4第11题)
详解
·选择性必修第一册·
第3课时 空间中直线、平面的垂直
1
学习目标
一、课程标准要求:
能用向量语言表述直线与直线、直线与平面、平面与平面的夹角以及
垂直与平行关系.
能用向量方法证明必修内容中有关直线、平面位置关系的判定定理.
2
1
学习目标
二、课时目标要求:
能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系,
发展数学抽象素养.
能用向量方法证明必修内容中有关直线、平面垂直关系的判定定理,
培养逻辑推理素养.
能用向量方法证明空间中直线、平面的垂直关系,培养逻辑推理素养.
2
3
引入新知
上节课学习了空间中直线、平面平行的向量表示,直线的方向向量和平面的法向量的对应关系是什么样的?
l1
l2
l
新课探究
问题1:类比空间中直线、平面平行关系的研究方法,你认为可以按怎样的路径研究空间中直线、平面的垂直关系
先给出直线、平面的向量表示式
利用向量运算得出方向向量、法向量之间的关系
利用方向向量、法向量之间的关系判断直线、平面的垂直关系.
新课探究
问题2:类比空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系
一般地,直线与直线垂直,就是两直线的方向向量垂直;
直线与平面垂直,就是直线的方向向量与平面的法向量平行;平面与平面垂直,就是两平面的法向量垂直.
新课探究
l1
l2
(1)
l
(2)
(3)
新课探究
思考:我们随时随地看到向量运算的作用,你同意“向量是躯体,运算是灵魂”“没有运算的向量只能起路标的作用”的说法吗?
有了向量的运算才能研究空间图形的位置关系、度量问题.向量的作用是通过其运算来体现的,如果没有运算,那么向量仅能表示空间中的点、直线和平面,只是“路标”,无法获得空间图形的几何性质.
应用新知
分析:
应用新知
方法一:
应用新知
方法一:
应用新知
方法二:
应用新知
方法二:
应用新知
反思感悟
利用向量方法证明线线垂直的方法——基向量法:
①取三个不共线的已知向量(通常是它们的模及其两两夹角为已知)为空间的一个基底;
②用基底把两直线的方向向量表示出来;
③利用向量的数量积计算出两直线的方向向量的数量积为0;
④由方向向量垂直得到两直线垂直.
应用新知
反思感悟
利用向量方法证明线线垂直的方法——坐标法:
①根据已知条件和图形特征,建立适当的空间直角坐标系,正确地写出各点的坐标;
②根据所求出的点的坐标求出两直线方向向量的坐标;
③计算两直线方向向量的数量积为0;
④由方向向量垂直得到两直线垂直.
应用新知
变式训练:
应用新知
变式训练:
应用新知
应用新知
方法一
应用新知
方法一
应用新知
方法二
应用新知
方法二
应用新知
方法三
应用新知
方法三
应用新知
反思感悟
利用空间向量证明线面垂直的方法——基向量法:
①确定基向量作为空间的一个基底,用基向量表示有关直线的方向向量;
②找出平面内两条相交直线的方向向量,并分别用基向量表示;
③分别计算有关直线的方向向量与平面内相交直线的向量的数量积,根据数量积为0,证得线线垂直,然后由线面垂直的判定定理得出结论.
应用新知
反思感悟
利用空间向量证明线面垂直的方法——坐标法:
方法一:
①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③找出平面内两条相交直线,并用坐标表示它们的方向向量;
④分别计算两组向量的数量积,得到数量积为0,证得线线垂直,然后得出线面垂直.
应用新知
反思感悟
利用空间向量证明线面垂直的方法——坐标法:
方法二:
①建立空间直角坐标系;
②将直线的方向向量用坐标表示;
③求出平面的法向量;
④证明直线的方向向量与平面的法向量平行,得出线面垂直
应用新知
变式训练:
图1.4-14
应用新知
变式训练:
图1.4-14
应用新知
变式训练:
图1.4-14
应用新知
变式训练:
图1.4-14
应用新知
例3:证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,
则这两个平面垂直.
图1.4-15
分析:
证明:
应用新知
规律方法
利用空间向量证明线面垂直的方法
1.利用空间向量证明面面垂直的方法
(1)利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直,进而转化为线线垂直问题;
(2)直接求解两个平面的法向量,证明两个法向量垂直,从而得到两个平面垂直.
2.向量法证明面面垂直的优越性
主要体现在不必考虑图形的位置关系,恰当建系或用基向量表示后,只需经过向量运算就可得到要证明的结果,思路方法很“公式化”.
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
应用新知
变式训练:
能力提升
例题
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
应用新知
方法总结
应用空间向量解答探索性(存在性)问题
立体几何中的存在探究题,解决思路一般有两个:
(1)根据题目的已知条件进行综合分析和观察猜想,找出点或线的位置,并用向量表示出来,然后再加以证明,得出结论;
(2)假设所求的点或参数存在,并用相关参数表示相关点,根据线、面满足的垂直、平行关系,构建方程(组)求解,若能求出参数的值且符合该限定的范围,则存在,否则不存在.
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
解析
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
分析
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
变式训练
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
分析
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
能力提升
解析
题型一
利用空间向量解决空间中直线、平面垂直的探究性问题.
课堂小结
作业布置
巩固作业:教科书第33页练习第1题
教科书第42-43页习题1.4第5、8、11题
作业答案(教科书第33页练习第1题)
详解
作业答案(教科书第42-43页习题1.4第5题)
详解
作业答案(教科书第42-43页习题1.4第5题)
详解
作业答案(教科书第42-43页习题1.4第8题)
详解
作业答案(教科书第42-43页习题1.4第8题)
详解
作业答案(教科书第42-43页习题1.4第11题)
详解
作业答案(教科书第42-43页习题1.4第11题)
详解
