人教A版高中数学选择性必修第一册1.4.2用空间向量研究距离问题(第1课时) 课件(共70张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.2用空间向量研究距离问题(第1课时) 课件(共70张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:39:02 | ||
图片预览









文档简介
(共70张PPT)
·选择性必修第一册·
第1课时 用空间向量研究距离问题
学习目标
一、课程标准要求:
能用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的平面的距离问题 (参见案例16) 和简单夹角问题,并能描述解决这一类问题的程序,体会向量方法在研究几何问题中的作用。
学习目标
1
二、课时目标要求:
向量语言表述空间距离,理解运用向量运算求解空间距离的原理,
培养数学抽象、逻辑推理素养.
能应用空间向量法解决距离问题,培养数学运算素养.
理解空间向量解决立体几何中的问题的“三步曲”.
2
3
引入新知
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
新课探究
我们知道,立体几何中的距离问题包括点到直线、点到平面、两条平行直线以及两个平行平面的距离问题等.如何用空间向量解决这些距离问题呢?
两点间的距离是根本,点到直线的距离和点到平面的距离是基础,其他距离问题都可以转化为这两类距离问题.
下面我们先研究用向量方法求直线l外一点P到直线l的距离.
新课探究
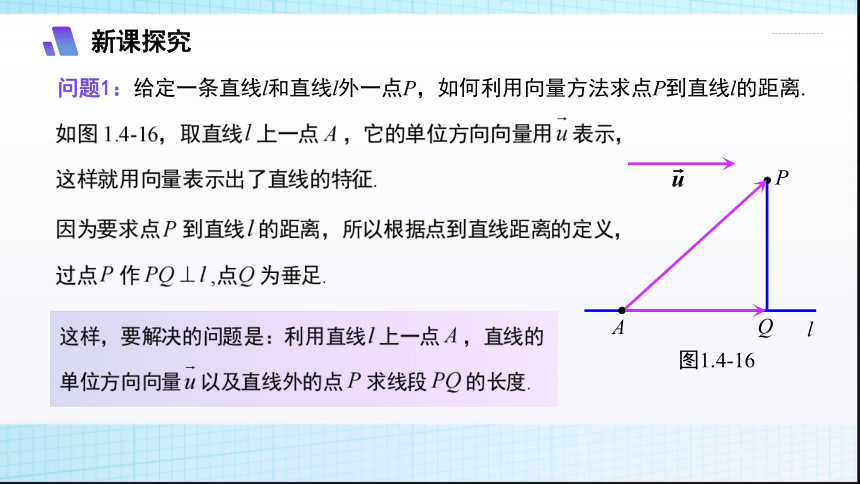
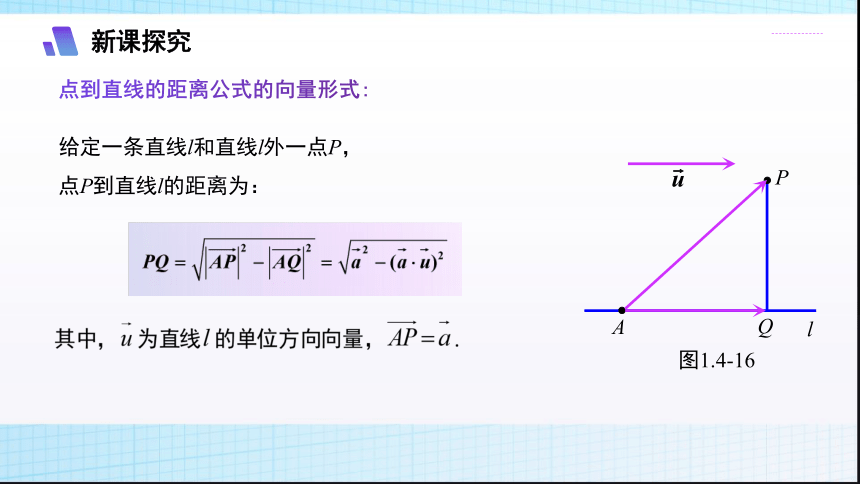
问题1:给定一条直线l和直线l外一点P,如何利用向量方法求点P到直线l的距离.
A
P
Q
l
图1.4-16
新课探究
A
P
Q
l
图1.4-16
新课探究
A
P
Q
l
图1.4-16
给定一条直线l和直线l外一点P,
点P到直线l的距离为:
新课探究
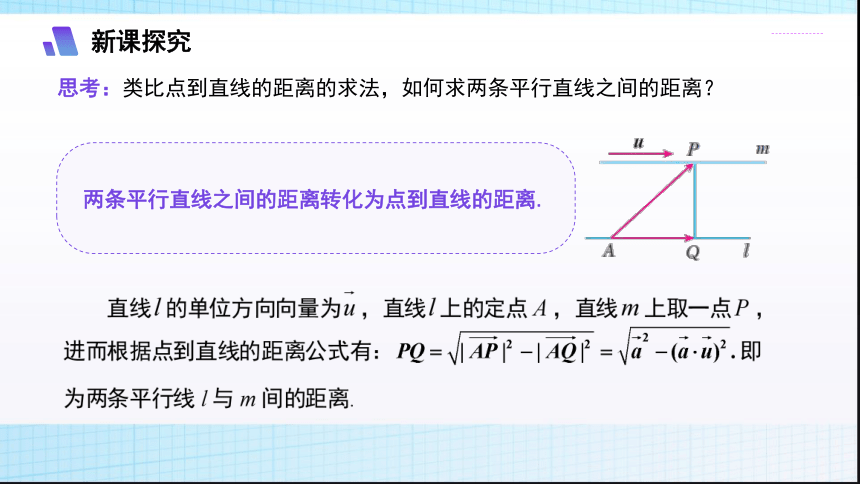
思考:类比点到直线的距离的求法,如何求两条平行直线之间的距离?
两条平行直线之间的距离转化为点到直线的距离.
新课探究
问题3:你能类比点到直线的距离公式的推导过程,推导出点到平面的距离公式吗 请大家自主探究.探究过程中要注意思考如下问题:
Q
P
l
n
α
A
新课探究
图1.4-17
新课探究
图1.4-17
第一步
第二步
第三步
第四步
新课探究
图1.4-17
图1.4-16
思考:点到平面的距离公式和点到直线的距离公式区别在哪里 为什么会有这样的区别
新课探究
图1.4-17
转化
转化
新课探究
点线距、线线距
点面距、线面距、面面距
图1.4-17
图1.4-16
应用新知
例1
根据条件建立空间直角坐标系,用坐标表示相关的点、直线的方向向量和平面的法向量,再利用有关公式,通过坐标运算得出相应的距离.
【分析】
图1.4-18
应用新知
例1
图1.4-18
解:
应用新知
例1
图1.4-18
应用新知
例1
图1.4-18
应用新知
例1
图1.4-18
方法规律
空间向量解决立体几何问题的“三步曲”
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
应用新知
问题5: 结合例1,回顾用空间向量解决距离问题的过程,你能总结用向量方法解决立体几何问题的基本步骤吗
方法规律
应用新知
方法规律
应用新知
应用新知
变式
练习
【解析】
应用新知
变式
练习
应用新知
变式
练习
应用新知
变式
练习
应用新知
变式
练习
能力提升
题型一
求空间两点间的距离问题
例题
能力提升
题型一
求空间两点间的距离问题
解析
能力提升
题型一
求空间两点间的距离问题
解析
方法总结
应用新知
能力提升
题型一
求空间两点间的距离问题
变式训练
能力提升
题型一
求空间两点间的距离问题
解析
能力提升
题型一
求空间两点间的距离问题
解析
能力提升
题型二
空间点到平面距离的几种求解方法
例题
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法总结
应用新知
方法总结
应用新知
能力提升
题型二
空间点到平面距离的几种求解方法
变式训练
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
变式训练
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法一:等体积法
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法二:直接法
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法二:直接法
能力提升
题型二
空间点到平面距离的几种求解方法
变式训练
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
转化法 + 等体积法
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
课堂小结
作业布置
巩固作业:教科书第35页练习第1、3题;
教科书第40页习题第6、7题;
教科书第44页习题第13题.
课后作业答案
教科书第35页练习第1题
课后作业答案
教科书第35页练习第3题
课后作业答案
教科书第40页习题1.4第6题
课后作业答案
教科书第40页习题1.4第7题
课后作业答案
教科书第40页习题1.4第7题
课后作业答案
教科书第44页习题1.4第13题
课后作业答案
教科书第44页习题1.4第13题
·选择性必修第一册·
第1课时 用空间向量研究距离问题
学习目标
一、课程标准要求:
能用向量方法解决点到直线、点到平面、相互平行的直线、相互平行的平面的距离问题 (参见案例16) 和简单夹角问题,并能描述解决这一类问题的程序,体会向量方法在研究几何问题中的作用。
学习目标
1
二、课时目标要求:
向量语言表述空间距离,理解运用向量运算求解空间距离的原理,
培养数学抽象、逻辑推理素养.
能应用空间向量法解决距离问题,培养数学运算素养.
理解空间向量解决立体几何中的问题的“三步曲”.
2
3
引入新知
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
新课探究
我们知道,立体几何中的距离问题包括点到直线、点到平面、两条平行直线以及两个平行平面的距离问题等.如何用空间向量解决这些距离问题呢?
两点间的距离是根本,点到直线的距离和点到平面的距离是基础,其他距离问题都可以转化为这两类距离问题.
下面我们先研究用向量方法求直线l外一点P到直线l的距离.
新课探究
问题1:给定一条直线l和直线l外一点P,如何利用向量方法求点P到直线l的距离.
A
P
Q
l
图1.4-16
新课探究
A
P
Q
l
图1.4-16
新课探究
A
P
Q
l
图1.4-16
给定一条直线l和直线l外一点P,
点P到直线l的距离为:
新课探究
思考:类比点到直线的距离的求法,如何求两条平行直线之间的距离?
两条平行直线之间的距离转化为点到直线的距离.
新课探究
问题3:你能类比点到直线的距离公式的推导过程,推导出点到平面的距离公式吗 请大家自主探究.探究过程中要注意思考如下问题:
Q
P
l
n
α
A
新课探究
图1.4-17
新课探究
图1.4-17
第一步
第二步
第三步
第四步
新课探究
图1.4-17
图1.4-16
思考:点到平面的距离公式和点到直线的距离公式区别在哪里 为什么会有这样的区别
新课探究
图1.4-17
转化
转化
新课探究
点线距、线线距
点面距、线面距、面面距
图1.4-17
图1.4-16
应用新知
例1
根据条件建立空间直角坐标系,用坐标表示相关的点、直线的方向向量和平面的法向量,再利用有关公式,通过坐标运算得出相应的距离.
【分析】
图1.4-18
应用新知
例1
图1.4-18
解:
应用新知
例1
图1.4-18
应用新知
例1
图1.4-18
应用新知
例1
图1.4-18
方法规律
空间向量解决立体几何问题的“三步曲”
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
应用新知
问题5: 结合例1,回顾用空间向量解决距离问题的过程,你能总结用向量方法解决立体几何问题的基本步骤吗
方法规律
应用新知
方法规律
应用新知
应用新知
变式
练习
【解析】
应用新知
变式
练习
应用新知
变式
练习
应用新知
变式
练习
应用新知
变式
练习
能力提升
题型一
求空间两点间的距离问题
例题
能力提升
题型一
求空间两点间的距离问题
解析
能力提升
题型一
求空间两点间的距离问题
解析
方法总结
应用新知
能力提升
题型一
求空间两点间的距离问题
变式训练
能力提升
题型一
求空间两点间的距离问题
解析
能力提升
题型一
求空间两点间的距离问题
解析
能力提升
题型二
空间点到平面距离的几种求解方法
例题
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法总结
应用新知
方法总结
应用新知
能力提升
题型二
空间点到平面距离的几种求解方法
变式训练
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
变式训练
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法一:等体积法
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法二:直接法
能力提升
题型二
空间点到平面距离的几种求解方法
解析
方法二:直接法
能力提升
题型二
空间点到平面距离的几种求解方法
变式训练
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
转化法 + 等体积法
能力提升
题型二
空间点到平面距离的几种求解方法
解析
能力提升
题型二
空间点到平面距离的几种求解方法
解析
课堂小结
作业布置
巩固作业:教科书第35页练习第1、3题;
教科书第40页习题第6、7题;
教科书第44页习题第13题.
课后作业答案
教科书第35页练习第1题
课后作业答案
教科书第35页练习第3题
课后作业答案
教科书第40页习题1.4第6题
课后作业答案
教科书第40页习题1.4第7题
课后作业答案
教科书第40页习题1.4第7题
课后作业答案
教科书第44页习题1.4第13题
课后作业答案
教科书第44页习题1.4第13题
