人教A版高中数学选择性必修第一册2.1.2两条直线平行和垂直的判定 课件(共48张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册2.1.2两条直线平行和垂直的判定 课件(共48张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:39:52 | ||
图片预览











文档简介
(共48张PPT)
·选择性必修第一册·
1
学习目标
理解两条直线平行与垂直的条件,培养数学抽象的核心素养.
重点: 能根据斜率判定两条直线平行或垂直,强化数学运算的核心素养.
难点: 能利用两直线平行或垂直的条件解决问题,培养逻辑推理的核心
素养.
2
3
2.1.2两条直线平行和垂直的判定
01
创设背景,引入新知
过山车是一项富有刺激性的娱乐项目.实际上,过山车的运动包含了许多数学和物理学原理.
过山车的两条铁轨是相互平行的轨道,它们靠着一根根巨大的柱形钢筋支撑着,为了使设备安全,柱子之间还有一些小的钢筋连接,这些钢筋有的互相平行,有的互相垂直。
像这样我们生活中的还有很多平行和垂直,所以数学来源于生活。
那么,两条直线的平行与垂直用什么来刻画呢
创设背景,引入新知
为了在平面直角坐标系中用代数方法表示直线,我们从确定直线位置的几何要素出发,引入直线的倾斜角;
再利用倾斜角与直线上点的坐标关系引入直线的斜率,从数的角度刻画了直线相对于x轴的倾斜程度,并导出了用直线上任意两点的坐标计算斜率的公式,从而把几何问题转化为代数问题.
下面,我们通过直线的斜率判断两条直线的位置关系
2.1.2两条直线平行和垂直的判定
02
探究新知
思考:我们知道,平面中的两条直线有两种位置关系:相交、平行.
当两条直线l1与l2平行时,它们的斜率k1与k2满足什么关系?并论证你的结论.
因此,对于斜率分别为k1,k2的两条直线l1,l2,有
l1//l2 k1=k2
如图,若l1∥l2,则倾斜角分别为α1=α2,所以
tan α1=tan α2,即k1=k2.
因此,若l1∥l2,即k1=k2.
反之,若k1=k2,则tan α1=tan α2,所以α1=α2所以l1∥l2.
l1//l2
探究新知
注意:若没有特别说明,说“两条直线l1,l2”时,指两条不重合的直线.
追问:当α1=α2=90o时,直线l1与直线l2的斜率均不存在时,两直线是什么位置关系?
O
x
y
l1
l2
探究新知
总结:
类型
前提条件
对应关系
图示
斜率存在
斜率不存在
α1=α2 ≠ 90°
α1=α2=90°
l1//l2 k1=k2
l1//l2 两直线的斜率都不存在
探究新知
思考:如何利用斜率证明A、B、C三点共线?
第一步
第二步
斜率相等:说明求的两个斜率相等;
第三步
平行且共点:说明两条直线平行且共点;
第四步
下结论:所以三点共线.
应用新知
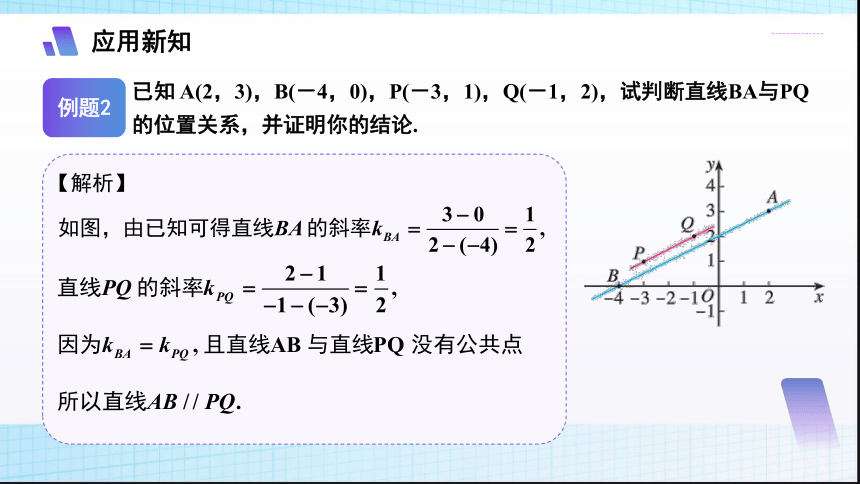
已知 A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
例题2
【解析】
应用新知
跟踪练习
【解析】
应用新知
变式练习
【解析】
应用新知
例题3
【解析】
应用新知
例题3
【解析】
探究新知
思考:如何利用斜率证明两条直线平行?
第一步
求斜率:分别求两条直线的斜率;
第二步
确定斜率关系:两个斜率相等或两个斜率均不存在;
第三步
检验:验证两条直线不重合;
第四步
下结论:所以两直线平行.
2.1.2两条直线平行和垂直的判定
03
探究新知
思考:当直线l1,l2垂直时,它们的斜率除了不相等外,是否还有特殊的
数量关系?
显然,当两条直线相交时,它们斜率不相等;
反之,当两条直线的斜率不相等时,它们相交.
在相交的位置关系中,垂直是最特殊的情形.
利用向量工具,考虑两条直线的方向向量垂直时,数量积时多少?
应用新知
问题1
问题2
应用新知
问题3
当直线l1的倾斜角为0°时,若直线l1⊥l2,则l2的斜率应满足什么条件?
如图,当直线l1的倾斜角为0°时,
若l1⊥l2,则l2的倾斜角为90°,
此时直线l2的斜率不存在.
探究新知
总结:
类型
前提条件
对应关系
图示
斜率都存在
l1(或l2)的斜率不存在
α1 ≠ 90°,且α2 ≠ 90°
α1=90°(或α2=90°)
l1⊥l2 k1k2= -1
l1⊥l2 l1(或l2)的斜率为0
应用新知
例题4
【解析】
应用新知
跟踪练习
【解析】
跟踪练习
【解析】
应用新知
例题5
【分析】
【解析】
探究新知
思考:如何利用斜率证明两条直线垂直?
第一步
求斜率:分别求两条直线的斜率;
第二步
确定斜率关系:两个斜率乘积等于-1 或一个斜率不存在、一个斜率为0;
第三步
下结论:所以两直线平行.
能力提升
题型一
利用斜率判断平面图形的形状
例题
【解析】
故四边形ABCD是直角梯形.
方法总结: 可以先用点的坐标试着画出图形,预猜是什么图形,然后用斜率证明平行和垂直,证明图形的形状的猜想.
能力提升
题型二
已知直线平行关系求参数值
例题
方法总结: 由直线平行,得到两直线的斜率相等,利用该等式关系建立关于参数的方程,解方程即可得解. 注意斜率都不存在的情况.
【解析】
能力提升
题型三
已知直线垂直关系求参数值
例题
方法总结: 由直线垂直,得到两直线的斜率乘积等于-1,利用该等式关系
建立关于参数的方程,解方程即可得解.
注意斜率一个为0、一个不存在的情况.
【解析】
课堂小结
两条直线平行与垂直的判定
学习新知
详解
C
学习新知
A
详解
学习新知
A
详解
学习新知
1
详解
学习新知
详解
综上可知
a=0或1
学习新知
直角梯形
详解
作业布置
作业1:完成教材:第57页 练习 第1,2题。
作业2:完成教材:第57 页 习题2.1 第5,6,9,10题。
课后作业答案
练习(第57页)
课后作业答案
练习(第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
y
P
O
A
B
x
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
·选择性必修第一册·
1
学习目标
理解两条直线平行与垂直的条件,培养数学抽象的核心素养.
重点: 能根据斜率判定两条直线平行或垂直,强化数学运算的核心素养.
难点: 能利用两直线平行或垂直的条件解决问题,培养逻辑推理的核心
素养.
2
3
2.1.2两条直线平行和垂直的判定
01
创设背景,引入新知
过山车是一项富有刺激性的娱乐项目.实际上,过山车的运动包含了许多数学和物理学原理.
过山车的两条铁轨是相互平行的轨道,它们靠着一根根巨大的柱形钢筋支撑着,为了使设备安全,柱子之间还有一些小的钢筋连接,这些钢筋有的互相平行,有的互相垂直。
像这样我们生活中的还有很多平行和垂直,所以数学来源于生活。
那么,两条直线的平行与垂直用什么来刻画呢
创设背景,引入新知
为了在平面直角坐标系中用代数方法表示直线,我们从确定直线位置的几何要素出发,引入直线的倾斜角;
再利用倾斜角与直线上点的坐标关系引入直线的斜率,从数的角度刻画了直线相对于x轴的倾斜程度,并导出了用直线上任意两点的坐标计算斜率的公式,从而把几何问题转化为代数问题.
下面,我们通过直线的斜率判断两条直线的位置关系
2.1.2两条直线平行和垂直的判定
02
探究新知
思考:我们知道,平面中的两条直线有两种位置关系:相交、平行.
当两条直线l1与l2平行时,它们的斜率k1与k2满足什么关系?并论证你的结论.
因此,对于斜率分别为k1,k2的两条直线l1,l2,有
l1//l2 k1=k2
如图,若l1∥l2,则倾斜角分别为α1=α2,所以
tan α1=tan α2,即k1=k2.
因此,若l1∥l2,即k1=k2.
反之,若k1=k2,则tan α1=tan α2,所以α1=α2所以l1∥l2.
l1//l2
探究新知
注意:若没有特别说明,说“两条直线l1,l2”时,指两条不重合的直线.
追问:当α1=α2=90o时,直线l1与直线l2的斜率均不存在时,两直线是什么位置关系?
O
x
y
l1
l2
探究新知
总结:
类型
前提条件
对应关系
图示
斜率存在
斜率不存在
α1=α2 ≠ 90°
α1=α2=90°
l1//l2 k1=k2
l1//l2 两直线的斜率都不存在
探究新知
思考:如何利用斜率证明A、B、C三点共线?
第一步
第二步
斜率相等:说明求的两个斜率相等;
第三步
平行且共点:说明两条直线平行且共点;
第四步
下结论:所以三点共线.
应用新知
已知 A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
例题2
【解析】
应用新知
跟踪练习
【解析】
应用新知
变式练习
【解析】
应用新知
例题3
【解析】
应用新知
例题3
【解析】
探究新知
思考:如何利用斜率证明两条直线平行?
第一步
求斜率:分别求两条直线的斜率;
第二步
确定斜率关系:两个斜率相等或两个斜率均不存在;
第三步
检验:验证两条直线不重合;
第四步
下结论:所以两直线平行.
2.1.2两条直线平行和垂直的判定
03
探究新知
思考:当直线l1,l2垂直时,它们的斜率除了不相等外,是否还有特殊的
数量关系?
显然,当两条直线相交时,它们斜率不相等;
反之,当两条直线的斜率不相等时,它们相交.
在相交的位置关系中,垂直是最特殊的情形.
利用向量工具,考虑两条直线的方向向量垂直时,数量积时多少?
应用新知
问题1
问题2
应用新知
问题3
当直线l1的倾斜角为0°时,若直线l1⊥l2,则l2的斜率应满足什么条件?
如图,当直线l1的倾斜角为0°时,
若l1⊥l2,则l2的倾斜角为90°,
此时直线l2的斜率不存在.
探究新知
总结:
类型
前提条件
对应关系
图示
斜率都存在
l1(或l2)的斜率不存在
α1 ≠ 90°,且α2 ≠ 90°
α1=90°(或α2=90°)
l1⊥l2 k1k2= -1
l1⊥l2 l1(或l2)的斜率为0
应用新知
例题4
【解析】
应用新知
跟踪练习
【解析】
跟踪练习
【解析】
应用新知
例题5
【分析】
【解析】
探究新知
思考:如何利用斜率证明两条直线垂直?
第一步
求斜率:分别求两条直线的斜率;
第二步
确定斜率关系:两个斜率乘积等于-1 或一个斜率不存在、一个斜率为0;
第三步
下结论:所以两直线平行.
能力提升
题型一
利用斜率判断平面图形的形状
例题
【解析】
故四边形ABCD是直角梯形.
方法总结: 可以先用点的坐标试着画出图形,预猜是什么图形,然后用斜率证明平行和垂直,证明图形的形状的猜想.
能力提升
题型二
已知直线平行关系求参数值
例题
方法总结: 由直线平行,得到两直线的斜率相等,利用该等式关系建立关于参数的方程,解方程即可得解. 注意斜率都不存在的情况.
【解析】
能力提升
题型三
已知直线垂直关系求参数值
例题
方法总结: 由直线垂直,得到两直线的斜率乘积等于-1,利用该等式关系
建立关于参数的方程,解方程即可得解.
注意斜率一个为0、一个不存在的情况.
【解析】
课堂小结
两条直线平行与垂直的判定
学习新知
详解
C
学习新知
A
详解
学习新知
A
详解
学习新知
1
详解
学习新知
详解
综上可知
a=0或1
学习新知
直角梯形
详解
作业布置
作业1:完成教材:第57页 练习 第1,2题。
作业2:完成教材:第57 页 习题2.1 第5,6,9,10题。
课后作业答案
练习(第57页)
课后作业答案
练习(第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
y
P
O
A
B
x
课后作业答案
习题2.1 (第57页)
课后作业答案
习题2.1 (第57页)
