人教A版高中数学选择性必修第一册1.4.2用空间向量研究夹角问题(第2课时) 课件(共73张PPT)
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.4.2用空间向量研究夹角问题(第2课时) 课件(共73张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 40.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 19:41:49 | ||
图片预览









文档简介
(共73张PPT)
·选择性必修第一册·
第2课时 用空间向量研究空间角度问题
学习目标
一、课程标准要求:
能用向量方法解决简单夹角问题,并能描述解决这一类问题的程序,体会向量方法在研究几何问题中的作用。
学习目标
二、课时目标要求:
理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法
求两异面直线所成角,发展直观想象,数学运算素养.
理解直线与平面所成角与直线方向向量和平面法向量夹角之间的关系,
会用向量方法求直线与平面所成角,发展直观想象,数学运算素养.
理解二面角大小与两个面法向量夹角之间的关系,会用向量方法求二
面角的大小,发展直观想象,数学运算素养.
1
2
3
引入新知
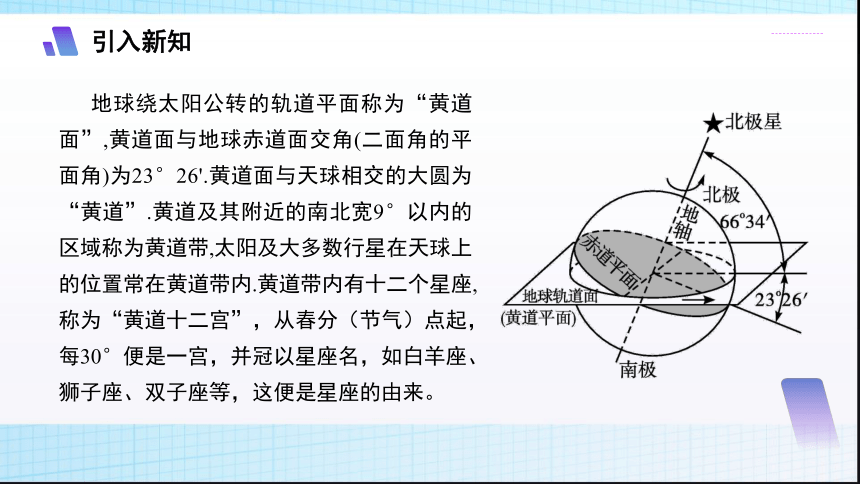
地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面交角(二面角的平面角)为23°26'.黄道面与天球相交的大圆为“黄道”.黄道及其附近的南北宽9°以内的区域称为黄道带,太阳及大多数行星在天球上的位置常在黄道带内.黄道带内有十二个星座,称为“黄道十二宫”,从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、狮子座、双子座等,这便是星座的由来。
新课探究
与距离一样,角度是立体几何中的另一类度量问题.本质上,角度是对两个方向的差的度量,向量是有方向的量,所以利用向量研究角度问题有其独特的优势.请同学们先看问题1.
新课探究
图1.4-19
新课探究
图1.4-19
化为向量问题
新课探究
图1.4-19
新课探究
图1.4-19
进行向量问题
新课探究
图1.4-19
回到图形问题
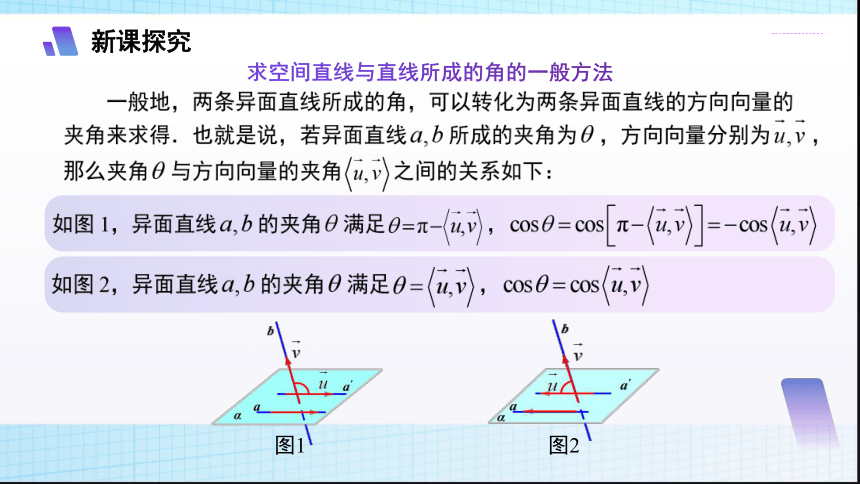
追问:回顾问题1的求解过程,你能归纳出利用向量求空间直线与直线所成的角的一般方法吗 其基本步骤是怎样的?
新课探究
图1
图2
新课探究
求空间直线与直线所成的角基本步骤
几何问题
向量问题
向量运算
几何解释
新课探究
问题2:类比直线与直线夹角的向量解决步骤,一般地,如何求直线与平面所成的角 如何将几何问题转化为向量问题
点与方向向量
点与法向量
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.
新课探究
图1.4-20(1)
图1.4-20(2)
新课探究
问题3: 类比已有的直线、平面所成角的定义,你认为应如何合理定义两个平面所成的角 进一步地,如何求平面和平面的夹角
图1.4-21
新课探究
图1.4-21(1)
图1.4-21(2)
新课探究
追问: 你能说说平面与平面的夹角与二面角的区别和联系吗
新课探究
范围
图形
公式
异面直线
所成角
直线与平
面所成角
平面与平
面所成角
应用新知
例8
图1.4-22
【分析】
应用新知
例8
图1.4-22
应用新知
例8
图1.4-22
应用新知
例8
图1.4-22
应用新知
例8
图1.4-22
方法规律
应用新知
用向量法求两平面夹角的大小,可以避免作出二面角的平面角这一难点,转化为计算两半平面法向量的夹角问题,具体求解步骤如下:
(1)建立空间直角坐标系;
(2)分别求出二面角的两个半平面所在平面的法向量;
(3)求两个法向量的夹角;
(4)确定两平面夹角的大小.
向量法求两平面夹角的步骤
应用新知
变式
练习
【解析】
应用新知
变式
练习
应用新知
变式
练习
应用新知
例9
图1.4-23
应用新知
例9
图1.4-23
图1.4-24
应用新知
例9
图1.4-24
应用新知
例10
图1.4-25
【分析】
本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角,这些问题都可以利用向量方法解决.由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标系,用向量及坐标表示问题中的几何元素,进而解决问题.
应用新知
例10
图1.4-25
图1.4-26
应用新知
例10
图1.4-26
应用新知
例10
图1.4-26
应用新知
例10
图1.4-26
应用新知
例10
图1.4-26
能力提升
题型一
异面直线所成角的求解
例题
解析
【方法1,坐标法】
能力提升
题型一
异面直线所成角的求解
解析
【方法2,基向量法】
能力提升
题型一
异面直线所成角的求解
解析
【方法3,几何法】
方法总结
应用新知
求异面直线所成的角的两种方法
能力提升
题型一
异面直线所成角的求解
变式训练
解析
【方法一:向量法】
能力提升
题型一
异面直线所成角的求解
变式训练
解析
【方法二:几何法】
能力提升
题型二
空间直线与平面所成角的求解
例题
解析
【方法1,坐标法】
能力提升
题型二
空间直线与平面所成角的求解
例题
解析
【方法2,几何法】
方法总结
应用新知
求空间直线与平面所成角的方法
几何法
向量法
能力提升
题型二
空间直线与平面所成角的求解
变式训练
解析
能力提升
题型三
平面角与二面角问题
例题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
方法总结
应用新知
向量法求二面角的步骤
能力提升
变式训练
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
课堂小结
作业布置
巩固作业:教科书第41页练习第1题;
教科书第43-44页习题1.4第9、10、14题.
课后作业答案
教科书第41页练习第1题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
·选择性必修第一册·
第2课时 用空间向量研究空间角度问题
学习目标
一、课程标准要求:
能用向量方法解决简单夹角问题,并能描述解决这一类问题的程序,体会向量方法在研究几何问题中的作用。
学习目标
二、课时目标要求:
理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法
求两异面直线所成角,发展直观想象,数学运算素养.
理解直线与平面所成角与直线方向向量和平面法向量夹角之间的关系,
会用向量方法求直线与平面所成角,发展直观想象,数学运算素养.
理解二面角大小与两个面法向量夹角之间的关系,会用向量方法求二
面角的大小,发展直观想象,数学运算素养.
1
2
3
引入新知
地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面交角(二面角的平面角)为23°26'.黄道面与天球相交的大圆为“黄道”.黄道及其附近的南北宽9°以内的区域称为黄道带,太阳及大多数行星在天球上的位置常在黄道带内.黄道带内有十二个星座,称为“黄道十二宫”,从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、狮子座、双子座等,这便是星座的由来。
新课探究
与距离一样,角度是立体几何中的另一类度量问题.本质上,角度是对两个方向的差的度量,向量是有方向的量,所以利用向量研究角度问题有其独特的优势.请同学们先看问题1.
新课探究
图1.4-19
新课探究
图1.4-19
化为向量问题
新课探究
图1.4-19
新课探究
图1.4-19
进行向量问题
新课探究
图1.4-19
回到图形问题
追问:回顾问题1的求解过程,你能归纳出利用向量求空间直线与直线所成的角的一般方法吗 其基本步骤是怎样的?
新课探究
图1
图2
新课探究
求空间直线与直线所成的角基本步骤
几何问题
向量问题
向量运算
几何解释
新课探究
问题2:类比直线与直线夹角的向量解决步骤,一般地,如何求直线与平面所成的角 如何将几何问题转化为向量问题
点与方向向量
点与法向量
类似地,直线与平面所成的角,可以转化为直线的方向向量与平面的法向量的夹角.
新课探究
图1.4-20(1)
图1.4-20(2)
新课探究
问题3: 类比已有的直线、平面所成角的定义,你认为应如何合理定义两个平面所成的角 进一步地,如何求平面和平面的夹角
图1.4-21
新课探究
图1.4-21(1)
图1.4-21(2)
新课探究
追问: 你能说说平面与平面的夹角与二面角的区别和联系吗
新课探究
范围
图形
公式
异面直线
所成角
直线与平
面所成角
平面与平
面所成角
应用新知
例8
图1.4-22
【分析】
应用新知
例8
图1.4-22
应用新知
例8
图1.4-22
应用新知
例8
图1.4-22
应用新知
例8
图1.4-22
方法规律
应用新知
用向量法求两平面夹角的大小,可以避免作出二面角的平面角这一难点,转化为计算两半平面法向量的夹角问题,具体求解步骤如下:
(1)建立空间直角坐标系;
(2)分别求出二面角的两个半平面所在平面的法向量;
(3)求两个法向量的夹角;
(4)确定两平面夹角的大小.
向量法求两平面夹角的步骤
应用新知
变式
练习
【解析】
应用新知
变式
练习
应用新知
变式
练习
应用新知
例9
图1.4-23
应用新知
例9
图1.4-23
图1.4-24
应用新知
例9
图1.4-24
应用新知
例10
图1.4-25
【分析】
本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角,这些问题都可以利用向量方法解决.由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标系,用向量及坐标表示问题中的几何元素,进而解决问题.
应用新知
例10
图1.4-25
图1.4-26
应用新知
例10
图1.4-26
应用新知
例10
图1.4-26
应用新知
例10
图1.4-26
应用新知
例10
图1.4-26
能力提升
题型一
异面直线所成角的求解
例题
解析
【方法1,坐标法】
能力提升
题型一
异面直线所成角的求解
解析
【方法2,基向量法】
能力提升
题型一
异面直线所成角的求解
解析
【方法3,几何法】
方法总结
应用新知
求异面直线所成的角的两种方法
能力提升
题型一
异面直线所成角的求解
变式训练
解析
【方法一:向量法】
能力提升
题型一
异面直线所成角的求解
变式训练
解析
【方法二:几何法】
能力提升
题型二
空间直线与平面所成角的求解
例题
解析
【方法1,坐标法】
能力提升
题型二
空间直线与平面所成角的求解
例题
解析
【方法2,几何法】
方法总结
应用新知
求空间直线与平面所成角的方法
几何法
向量法
能力提升
题型二
空间直线与平面所成角的求解
变式训练
解析
能力提升
题型三
平面角与二面角问题
例题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
方法总结
应用新知
向量法求二面角的步骤
能力提升
变式训练
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
能力提升
解析
题型三
平面角与二面角问题
课堂小结
作业布置
巩固作业:教科书第41页练习第1题;
教科书第43-44页习题1.4第9、10、14题.
课后作业答案
教科书第41页练习第1题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第9题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第10题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
课后作业答案
教科书第43页习题1.4第14题
