第二章一元二次方程 重难点复习练(含答案)2025-2026学年数学北师大版九年级上册
文档属性
| 名称 | 第二章一元二次方程 重难点复习练(含答案)2025-2026学年数学北师大版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 489.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 21:47:17 | ||
图片预览





文档简介
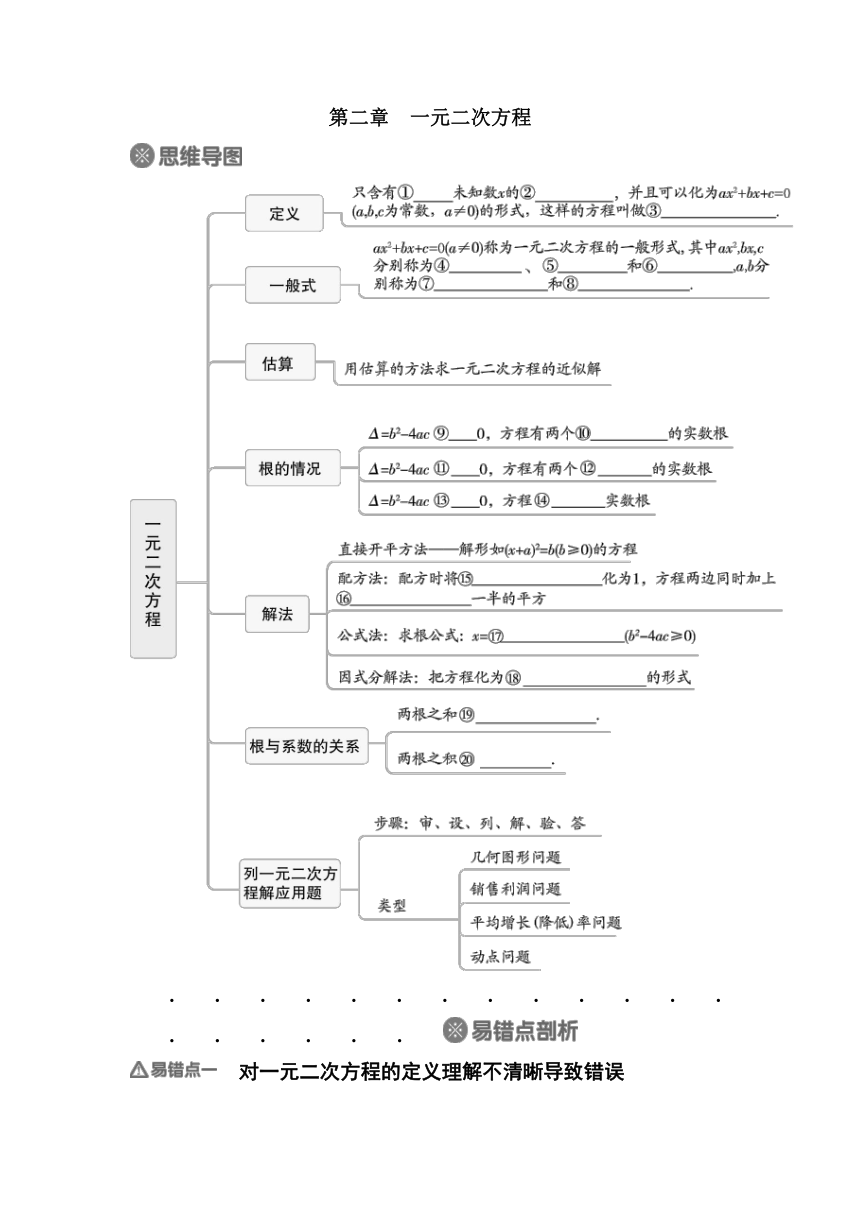
第二章 一元二次方程
. . . . . . . . . . . . . . . . . . .
对一元二次方程的定义理解不清晰导致错误
【例1】下列方程是一元二次方程的有 (只填序号).
①3x=x2,②x2=(x-3)2,③x2-3x=7,④=1,⑤x3 -3x=7,⑥x2-3y=7.
当我们判断一个方程是不是一元二次方程时,要注意以下几点:
1.判断时,方程要化为最简形式后才能进行;
2.必须有二次项,且二次项系数必须非0;
3.方程必须是整式方程;
4.方程中必须只有一个未知数,且未知数的最高次数是2.
1.(2023·深圳九年级联考)下列方程中,是一元二次方程的是( ).
A.+x=2 B.x2-4=4 C.5x2+3x+2y=0 D.x+5=1
2.(2024秋·深圳月考)下列方程一定是关于x的一元二次方程的是( ).
A.3x+1=x B.2x+y=5 C.+=1 D.x2-2x-3=0
在确定一元二次方程的各项系数时,经常漏了数字前面的符号而致错
【例2】(2023·深圳中学期中)将一元二次方程2x2=7x-5化成一般形式之后,一次项系数和常数项分别为( ).
A.-7,-5 B.5,-7 C.5,7 D.-7,5
1.要确定方程的各项系数,必须把方程化成一般形式;
2.对于方程来说,里面的“+”“-”是运算符号,当用来确定系数时,这些运算符号就变成了数的属性符号,表示是正数或负数.
3.(2023·深圳九年级校考)一元二次方程4x2+5x=81的二次项系数、一次项系数、常数项分别为( ).
A.4,5,81 B.4,5,-81 C.4,5,0 D.4x2,5x,-81
4.(2024秋·深圳月考)把一元二次方程(x+1)(x-1)=3x化成一般形式为 .
未知数指数中含有字母的一元二次方程,求字母值时,忽视一元二次方程的二次项系数不为0导致错误
【例3】(2023·佛山九年级校考阶段练习)若关于x的方程(m+1)-2x=3是一元二次方程,则m的值为( ).
A.1 B.-1 C.±1 D.0
一元二次方程满足的条件是
1.只含有一个未知数;
2.未知数的最高次数为2;
3.二次项系数不为0;
4.整式方程.
5.已知(m-1)-3x-5=0是一元二次方程,则m= .
6.关于x的方程(m-2)-2x+1=0是一元二次方程,则m的值为 .
已知二次项系数中含有字母,根据根的情形,求字母的取值范围时,忽视一元二次方程的二次项系数不为0导致错误
【例4】关于x的一元二次方程(a+1)x2-4x-1=0有实数根,则a的取值范围是 .
1.Δ=b2-4ac>0,方程有两个不相等的实数根;
2.Δ=b2-4ac=0,方程有两个相等的实数根;
3.Δ=b2-4ac<0,方程没有实数根;
4.根据方程根的情况,用Δ=b2-4ac列不等式确定字母的取值范围时不要忽视二次项系数不能为0这个条件.
7.(2024秋·光明区校级月考)关于x的一元二次方程(m-1)x2+2x-m2+1=0,常数项为0,则m值等于 .
8.若关于x的一元二次方程(m-1)x2+2mx+m-2=0有两个不相等的实数根,则m的取值范围是 .
一元二次方程的定义
(1)只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程;
(2)ax2+bx+c=0(a≠0)叫做一元二次方程的一般形式,ax2,bx,c分别称为二次项、一次项和常数项,a,b分别称为二次项系数和一次项系数.
1.下列方程是关于x的一元二次方程的是( ).
A.x2+=0 B.ax2+bx+c=0
C.(x-1)(x+2)=1 D.3x2-2xy+5=0
2.若方程(a-3)x2-x+1=0是关于x的一元二次方程,则a的取值范围是( ).
A.a≠3 B.a>3 C.a≥3 D.a<-3
3.(2025·深圳模拟)已知a是方程x2+2x=3的一个根,则代数式a2+2a+2 025的值为 .
4.把一元二次方程4(x+1)=5x2化为一般形式正确的是( ).
A.5x2-4x-4=0 B.5x2-4x+4=0
C.5x2+4x+4=0 D.5x2+4x-4=0
解一元二次方程——直接开平方法
(1)形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解;
(2)如果方程化成x2=p(p≥0)的形式,那么可得x=±;
(3)如果方程化成(nx+m)2=p(p≥0)的形式,那么nx+m=±.
5.解方程.
(1)4(x+2)2=25;
(2)(x-5)2-36=0;
(3)(x-5)2-9=0;
(4)2(x-1)2-18=0.
解一元二次方程——配方法
1.将一元二次方程配方成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.
2.用配方法解一元二次方程的步骤:
(1)把原方程化成ax2+bx+c=0(a≠0)的形式;
(2)方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;
(3)方程两边同时加上一次项系数一半的平方;
(4)把左边配方成一个完全平方式,右边化为一个常数;
(5)如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则此方程无实数解.
6.(2025·福田区一模)用配方法解方程x2+2x-1=0,下列配方正确的是( ).
A.(x+1)2=1 B.(x+1)2=2
C.(x-1)2=2 D.(x-1)2=1
7.方程x2+2x-2=0配方得到(x+m)2=3,则m= .
8.用配方法解方程.
(1)2x2-2x-1=0;
(2)2x2-4x=3.
解一元二次方程——公式法
1.一元二次方程ax2+bx+c=0(a≠0),当b2-4ac≥0时,方程有实数根,x=叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式.用求根公式解一元二次方程的方法叫做公式法.
2.用公式法解一元二次方程的步骤:
(1)把方程化成一般形式,进而确定a,b,c的值(注意符号);
(2)求出b2-4ac的值(若b2-4ac<0,方程无实数根);
(3)在b2-4ac≥0的前提下,把a,b,c的值代入求根公式进行计算,求出方程的根.
9.(2024·龙岗区校级开学)关于x的方程x2+mx-2=0根的情况是( ).
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
10.(2024秋·宝安区校级月考)若关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根,则k的取值范围是( ).
A.k<1 B.k<1且k≠0
C.k≠0 D.k>1
11.用公式法解方程.
(1)x2+4x+3=0;
(2)3x2-2x-2=0.
解一元二次方程——因式分解法
1.用因式分解法解一元二次方程的步骤:
(1)将方程右边化为0;
(2)将方程左边分解为两个一次因式的乘积;
(3)令这两个一次因式分别为0,得到两个一元一次方程;
(4)解这两个一元一次方程,它们的解就是原方程的解.
2.因式分解的常用方法:
提公因式法、公式法(完全平方公式、平方差公式)、十字相乘法等.
12.用因式分解法解方程.
(1)x2-2x-3=0;
(2)x(x-2)=x-2;
(3)x2-2x-15=0;
(4)(2x-1)2=(2-3x)2.
一元二次方程根与系数的关系
(1)设ax2+bx+c=0(a≠0)的两个根为x1,x2,则x1+x2=-,x1·x2=;(2)+=;(3) +=(x1 +x2 )2-2x1 x2 ;(4) (x1-x2)2=(x1+x2)2-4x1x2.
13.(2023·深圳九年级期中)若x1,x2是方程x2-7x-8=0的两个根,则( ).
A.x1+x2=7 B.x1+x2=-7 C.x1·x2= D.x1·x2=8
14.已知m,n是一元二次方程x2+4x-1=0的两根,则-的值是 .
15.已知关于x的一元二次方程(x+2)(x-3)=|k|.
(1)求证:对于任何实数k,方程总有两个不相等的实数根;
(2)设(x+2)(x-3)=|k|的两个实数根分别为x1,x2,若+=21,求k的值.
一元二次方程的应用
1.解决应用题的一般步骤:审、设、列、解、验、答.
2.解出方程后要根据题目的实际意义确定符合题意的解.
16.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( ).
A.200(1+a%)2=148 B.200(1-a%)2=148
C.200(1-2a%)=148 D.200(1-a2%)=148
17.(2024秋·增城区期末)某初中毕业班的每一个同学都将自己的相片向全班其他同学各送一张表示留念,全班共送了1 640张照片,如果全班有x名学生,根据题意,列出方程为( ).
A.x(x+1)=1 640 B.x(x+1)=1 640
C.x(x-1)=1 640 D.x(x-1)=1 640
18.(2025·深圳模拟)某校在科技节开幕式上,计划用一块正方形空地进行无人机表演,从这块空地上划出部分区域作为安全区(如图),原空地一边减少了4 m,另一边减少了2 m,剩余空地为起飞区.设原正方形空地的边长为x m.
(1)起飞区的边AB的长为 m(用含x的代数式表示);
(2)若起飞区的面积为120 m2,求原正方形空地的边长.
19.某文具专柜销售一种进价为40元/个的书包,当售价为60元/个时,日销售量为100个,国庆期间,通过市场调查发现这种书包的单价每降低2元,日销售量可增加20个.现准备每个书包降价x元销售,请回答:
(1)该专柜原来销售这种书包每天可获利 元;
(2)降价销售时,每个书包获利 元,每天可售出书包 个;
(3)若该专柜销售这种书包想要平均每天获利2 240元,并且要尽可能让利于顾客,赢得市场,则每个书包应降价多少元?
参考答案
【思维导图】
①一个 ②整式方程 ③一元二次方程 ④二次项 ⑤一次项 ⑥常数项 ⑦二次项系数 ⑧一次项系数 ⑨> ⑩不相等 = 相等 < 没有 二次项系数
一次项系数 (x+a)(x+b)=0 x1+x2=- x1x2=
【易错点剖析】
【例1】①③ 1.B 2.D
【例2】D 3.B 4.x2-3x-1=0
【例3】A 5.-3 6.-2
【例4】a≥-5且a≠-1 解析:∵一元二次方程(a+1)x2-4x-1=0有实数根,∴解得a≥-5且a≠-1.
7.-1 8.m>且m≠1
【重难点突破】
1.C 2.A 3.2 028 4.A
5.解:(1)4(x+2)2=25,∴(x+2)2=,
∴x+2=±,解得x1=,x2=-.
(2)(x-5)2-36=0,(x-5)2=36,x-5=±6,x=5±6,解得x1=11,x2=-1.
(3)(x-5)2-9=0,∴(x-5)2=9,
∴x-5=±3,∴x-5=3或x-5=-3,
∴x1=8,x2=2.
(4)2(x-1)2-18=0,∴2(x-1)2=18,∴(x-1)2=9,
∴x-1=±3,解得x1=4,x2=-2.
6.B 7.1
8.解:(1)2x2-2x-1=0,二次项系数化为1得x2-x-=0,
移项得x2-x=,配方得x2-x+(-)2=+(-)2,
即(x-)2=,∴x-=±,
解得x1=+,x2=-.
(2)2x2-4x=3,x2-2x=,x2-2x+1=,(x-1)2=,x-1=±,∴x1=1+,x2=1-.
9.A 10.B
11.解:(1)∵a=1,b=4,c=3,∴Δ=b2-4ac=42-4×1×3=16-12=4>0,∴x===-2±1,解得x1=-1,x2=-3.
(2)∵a=3,b=-2,c=-2,
∴Δ=b2-4ac=(-2)2-4×3×(-2)=28>0,
∴x====,∴x1=,x2=.
12.解:(1)x2-2x-3=0,(x-3)(x+1)=0,
x-3=0或x+1=0,解得x1=3,x2=-1.
(2)x(x-2)=x-2,移项,得x(x-2)-(x-2)=0,
因式分解得(x-2)(x-1)=0,
∴x-2=0或x-1=0,∴x1=2,x2=1.
(3)x2-2x-15=0,(x-5)(x+3)=0,x-5=0或x+3=0,
∴x1=5,x2=-3.
(4)(2x-1)2=(2-3x)2,(2x-1)2-(2-3x)2=0,
[(2x-1)-(2-3x)][(2x-1)+(2-3x)]=0,
(5x-3)(-x+1)=0,5x-3=0或-x+1=0,
解得x1=,x2=1.
13.A
14.4 解析:对于一元二次方程x2+4x-1=0,根据一元二次方程根与系数的关系,可得m+n=-=-4,mn==-1,所以-====4.故答案为4.
15.(1)证明:由题意可知,x2-x-6-|k|=0,
∴Δ=1+4(6+|k|)=25+4|k|>0,
∴对于任何实数k,方程总有两个不相等的实数根.
(2)解:原方程可化为x2-x-6-|k|=0,
∴x1+x2=1,x1x2=-6-|k|.
∵+=21,∴(x1+x2)2-2x1x2=21,
∴1-2(-6-|k|)=21,∴|k|=4,∴k=±4.
16.B 17.C
18.解:(1)根据题意,起飞区的边AB的长为(x-4)m,
故答案为(x-4).
解:(2)根据题意可得(x-2)(x-4)=120,
即x2-6x-112=0,解得x=14,x=-8(舍去).
答:原正方形空地的边长为14 m.
19.解:(1)根据题意得(60-40)×100=20×100=2 000(元),
∴该专柜原来销售这种书包每天可获利2 000元,
故答案为2 000.
解:(2)根据题意得,降价销售时,每个书包获利(60-40-x)=(20-x)元,
每天可售出书包(100+×20)=(100+10x)个.
故答案为(20-x);(100+10x).
解:(3)根据题意得(20-x)(100+10x)=2 240,
整理得x2-10x+24=0,解得x1=4,x2=6,
∵要尽可能让利于顾客,
∴x=6,∴每个书包应降价6元.
. . . . . . . . . . . . . . . . . . .
对一元二次方程的定义理解不清晰导致错误
【例1】下列方程是一元二次方程的有 (只填序号).
①3x=x2,②x2=(x-3)2,③x2-3x=7,④=1,⑤x3 -3x=7,⑥x2-3y=7.
当我们判断一个方程是不是一元二次方程时,要注意以下几点:
1.判断时,方程要化为最简形式后才能进行;
2.必须有二次项,且二次项系数必须非0;
3.方程必须是整式方程;
4.方程中必须只有一个未知数,且未知数的最高次数是2.
1.(2023·深圳九年级联考)下列方程中,是一元二次方程的是( ).
A.+x=2 B.x2-4=4 C.5x2+3x+2y=0 D.x+5=1
2.(2024秋·深圳月考)下列方程一定是关于x的一元二次方程的是( ).
A.3x+1=x B.2x+y=5 C.+=1 D.x2-2x-3=0
在确定一元二次方程的各项系数时,经常漏了数字前面的符号而致错
【例2】(2023·深圳中学期中)将一元二次方程2x2=7x-5化成一般形式之后,一次项系数和常数项分别为( ).
A.-7,-5 B.5,-7 C.5,7 D.-7,5
1.要确定方程的各项系数,必须把方程化成一般形式;
2.对于方程来说,里面的“+”“-”是运算符号,当用来确定系数时,这些运算符号就变成了数的属性符号,表示是正数或负数.
3.(2023·深圳九年级校考)一元二次方程4x2+5x=81的二次项系数、一次项系数、常数项分别为( ).
A.4,5,81 B.4,5,-81 C.4,5,0 D.4x2,5x,-81
4.(2024秋·深圳月考)把一元二次方程(x+1)(x-1)=3x化成一般形式为 .
未知数指数中含有字母的一元二次方程,求字母值时,忽视一元二次方程的二次项系数不为0导致错误
【例3】(2023·佛山九年级校考阶段练习)若关于x的方程(m+1)-2x=3是一元二次方程,则m的值为( ).
A.1 B.-1 C.±1 D.0
一元二次方程满足的条件是
1.只含有一个未知数;
2.未知数的最高次数为2;
3.二次项系数不为0;
4.整式方程.
5.已知(m-1)-3x-5=0是一元二次方程,则m= .
6.关于x的方程(m-2)-2x+1=0是一元二次方程,则m的值为 .
已知二次项系数中含有字母,根据根的情形,求字母的取值范围时,忽视一元二次方程的二次项系数不为0导致错误
【例4】关于x的一元二次方程(a+1)x2-4x-1=0有实数根,则a的取值范围是 .
1.Δ=b2-4ac>0,方程有两个不相等的实数根;
2.Δ=b2-4ac=0,方程有两个相等的实数根;
3.Δ=b2-4ac<0,方程没有实数根;
4.根据方程根的情况,用Δ=b2-4ac列不等式确定字母的取值范围时不要忽视二次项系数不能为0这个条件.
7.(2024秋·光明区校级月考)关于x的一元二次方程(m-1)x2+2x-m2+1=0,常数项为0,则m值等于 .
8.若关于x的一元二次方程(m-1)x2+2mx+m-2=0有两个不相等的实数根,则m的取值范围是 .
一元二次方程的定义
(1)只含有一个未知数,并且未知数的最高次数是2的整式方程,叫做一元二次方程;
(2)ax2+bx+c=0(a≠0)叫做一元二次方程的一般形式,ax2,bx,c分别称为二次项、一次项和常数项,a,b分别称为二次项系数和一次项系数.
1.下列方程是关于x的一元二次方程的是( ).
A.x2+=0 B.ax2+bx+c=0
C.(x-1)(x+2)=1 D.3x2-2xy+5=0
2.若方程(a-3)x2-x+1=0是关于x的一元二次方程,则a的取值范围是( ).
A.a≠3 B.a>3 C.a≥3 D.a<-3
3.(2025·深圳模拟)已知a是方程x2+2x=3的一个根,则代数式a2+2a+2 025的值为 .
4.把一元二次方程4(x+1)=5x2化为一般形式正确的是( ).
A.5x2-4x-4=0 B.5x2-4x+4=0
C.5x2+4x+4=0 D.5x2+4x-4=0
解一元二次方程——直接开平方法
(1)形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解;
(2)如果方程化成x2=p(p≥0)的形式,那么可得x=±;
(3)如果方程化成(nx+m)2=p(p≥0)的形式,那么nx+m=±.
5.解方程.
(1)4(x+2)2=25;
(2)(x-5)2-36=0;
(3)(x-5)2-9=0;
(4)2(x-1)2-18=0.
解一元二次方程——配方法
1.将一元二次方程配方成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.
2.用配方法解一元二次方程的步骤:
(1)把原方程化成ax2+bx+c=0(a≠0)的形式;
(2)方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;
(3)方程两边同时加上一次项系数一半的平方;
(4)把左边配方成一个完全平方式,右边化为一个常数;
(5)如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则此方程无实数解.
6.(2025·福田区一模)用配方法解方程x2+2x-1=0,下列配方正确的是( ).
A.(x+1)2=1 B.(x+1)2=2
C.(x-1)2=2 D.(x-1)2=1
7.方程x2+2x-2=0配方得到(x+m)2=3,则m= .
8.用配方法解方程.
(1)2x2-2x-1=0;
(2)2x2-4x=3.
解一元二次方程——公式法
1.一元二次方程ax2+bx+c=0(a≠0),当b2-4ac≥0时,方程有实数根,x=叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式.用求根公式解一元二次方程的方法叫做公式法.
2.用公式法解一元二次方程的步骤:
(1)把方程化成一般形式,进而确定a,b,c的值(注意符号);
(2)求出b2-4ac的值(若b2-4ac<0,方程无实数根);
(3)在b2-4ac≥0的前提下,把a,b,c的值代入求根公式进行计算,求出方程的根.
9.(2024·龙岗区校级开学)关于x的方程x2+mx-2=0根的情况是( ).
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
10.(2024秋·宝安区校级月考)若关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根,则k的取值范围是( ).
A.k<1 B.k<1且k≠0
C.k≠0 D.k>1
11.用公式法解方程.
(1)x2+4x+3=0;
(2)3x2-2x-2=0.
解一元二次方程——因式分解法
1.用因式分解法解一元二次方程的步骤:
(1)将方程右边化为0;
(2)将方程左边分解为两个一次因式的乘积;
(3)令这两个一次因式分别为0,得到两个一元一次方程;
(4)解这两个一元一次方程,它们的解就是原方程的解.
2.因式分解的常用方法:
提公因式法、公式法(完全平方公式、平方差公式)、十字相乘法等.
12.用因式分解法解方程.
(1)x2-2x-3=0;
(2)x(x-2)=x-2;
(3)x2-2x-15=0;
(4)(2x-1)2=(2-3x)2.
一元二次方程根与系数的关系
(1)设ax2+bx+c=0(a≠0)的两个根为x1,x2,则x1+x2=-,x1·x2=;(2)+=;(3) +=(x1 +x2 )2-2x1 x2 ;(4) (x1-x2)2=(x1+x2)2-4x1x2.
13.(2023·深圳九年级期中)若x1,x2是方程x2-7x-8=0的两个根,则( ).
A.x1+x2=7 B.x1+x2=-7 C.x1·x2= D.x1·x2=8
14.已知m,n是一元二次方程x2+4x-1=0的两根,则-的值是 .
15.已知关于x的一元二次方程(x+2)(x-3)=|k|.
(1)求证:对于任何实数k,方程总有两个不相等的实数根;
(2)设(x+2)(x-3)=|k|的两个实数根分别为x1,x2,若+=21,求k的值.
一元二次方程的应用
1.解决应用题的一般步骤:审、设、列、解、验、答.
2.解出方程后要根据题目的实际意义确定符合题意的解.
16.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( ).
A.200(1+a%)2=148 B.200(1-a%)2=148
C.200(1-2a%)=148 D.200(1-a2%)=148
17.(2024秋·增城区期末)某初中毕业班的每一个同学都将自己的相片向全班其他同学各送一张表示留念,全班共送了1 640张照片,如果全班有x名学生,根据题意,列出方程为( ).
A.x(x+1)=1 640 B.x(x+1)=1 640
C.x(x-1)=1 640 D.x(x-1)=1 640
18.(2025·深圳模拟)某校在科技节开幕式上,计划用一块正方形空地进行无人机表演,从这块空地上划出部分区域作为安全区(如图),原空地一边减少了4 m,另一边减少了2 m,剩余空地为起飞区.设原正方形空地的边长为x m.
(1)起飞区的边AB的长为 m(用含x的代数式表示);
(2)若起飞区的面积为120 m2,求原正方形空地的边长.
19.某文具专柜销售一种进价为40元/个的书包,当售价为60元/个时,日销售量为100个,国庆期间,通过市场调查发现这种书包的单价每降低2元,日销售量可增加20个.现准备每个书包降价x元销售,请回答:
(1)该专柜原来销售这种书包每天可获利 元;
(2)降价销售时,每个书包获利 元,每天可售出书包 个;
(3)若该专柜销售这种书包想要平均每天获利2 240元,并且要尽可能让利于顾客,赢得市场,则每个书包应降价多少元?
参考答案
【思维导图】
①一个 ②整式方程 ③一元二次方程 ④二次项 ⑤一次项 ⑥常数项 ⑦二次项系数 ⑧一次项系数 ⑨> ⑩不相等 = 相等 < 没有 二次项系数
一次项系数 (x+a)(x+b)=0 x1+x2=- x1x2=
【易错点剖析】
【例1】①③ 1.B 2.D
【例2】D 3.B 4.x2-3x-1=0
【例3】A 5.-3 6.-2
【例4】a≥-5且a≠-1 解析:∵一元二次方程(a+1)x2-4x-1=0有实数根,∴解得a≥-5且a≠-1.
7.-1 8.m>且m≠1
【重难点突破】
1.C 2.A 3.2 028 4.A
5.解:(1)4(x+2)2=25,∴(x+2)2=,
∴x+2=±,解得x1=,x2=-.
(2)(x-5)2-36=0,(x-5)2=36,x-5=±6,x=5±6,解得x1=11,x2=-1.
(3)(x-5)2-9=0,∴(x-5)2=9,
∴x-5=±3,∴x-5=3或x-5=-3,
∴x1=8,x2=2.
(4)2(x-1)2-18=0,∴2(x-1)2=18,∴(x-1)2=9,
∴x-1=±3,解得x1=4,x2=-2.
6.B 7.1
8.解:(1)2x2-2x-1=0,二次项系数化为1得x2-x-=0,
移项得x2-x=,配方得x2-x+(-)2=+(-)2,
即(x-)2=,∴x-=±,
解得x1=+,x2=-.
(2)2x2-4x=3,x2-2x=,x2-2x+1=,(x-1)2=,x-1=±,∴x1=1+,x2=1-.
9.A 10.B
11.解:(1)∵a=1,b=4,c=3,∴Δ=b2-4ac=42-4×1×3=16-12=4>0,∴x===-2±1,解得x1=-1,x2=-3.
(2)∵a=3,b=-2,c=-2,
∴Δ=b2-4ac=(-2)2-4×3×(-2)=28>0,
∴x====,∴x1=,x2=.
12.解:(1)x2-2x-3=0,(x-3)(x+1)=0,
x-3=0或x+1=0,解得x1=3,x2=-1.
(2)x(x-2)=x-2,移项,得x(x-2)-(x-2)=0,
因式分解得(x-2)(x-1)=0,
∴x-2=0或x-1=0,∴x1=2,x2=1.
(3)x2-2x-15=0,(x-5)(x+3)=0,x-5=0或x+3=0,
∴x1=5,x2=-3.
(4)(2x-1)2=(2-3x)2,(2x-1)2-(2-3x)2=0,
[(2x-1)-(2-3x)][(2x-1)+(2-3x)]=0,
(5x-3)(-x+1)=0,5x-3=0或-x+1=0,
解得x1=,x2=1.
13.A
14.4 解析:对于一元二次方程x2+4x-1=0,根据一元二次方程根与系数的关系,可得m+n=-=-4,mn==-1,所以-====4.故答案为4.
15.(1)证明:由题意可知,x2-x-6-|k|=0,
∴Δ=1+4(6+|k|)=25+4|k|>0,
∴对于任何实数k,方程总有两个不相等的实数根.
(2)解:原方程可化为x2-x-6-|k|=0,
∴x1+x2=1,x1x2=-6-|k|.
∵+=21,∴(x1+x2)2-2x1x2=21,
∴1-2(-6-|k|)=21,∴|k|=4,∴k=±4.
16.B 17.C
18.解:(1)根据题意,起飞区的边AB的长为(x-4)m,
故答案为(x-4).
解:(2)根据题意可得(x-2)(x-4)=120,
即x2-6x-112=0,解得x=14,x=-8(舍去).
答:原正方形空地的边长为14 m.
19.解:(1)根据题意得(60-40)×100=20×100=2 000(元),
∴该专柜原来销售这种书包每天可获利2 000元,
故答案为2 000.
解:(2)根据题意得,降价销售时,每个书包获利(60-40-x)=(20-x)元,
每天可售出书包(100+×20)=(100+10x)个.
故答案为(20-x);(100+10x).
解:(3)根据题意得(20-x)(100+10x)=2 240,
整理得x2-10x+24=0,解得x1=4,x2=6,
∵要尽可能让利于顾客,
∴x=6,∴每个书包应降价6元.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
