第六章反比例函数 重难点分类练(含答案)2025-2026学年数学北师大版九年级上册
文档属性
| 名称 | 第六章反比例函数 重难点分类练(含答案)2025-2026学年数学北师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 871.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 21:48:14 | ||
图片预览




文档简介
第六章 反比例函数
. . . . . . . . .
反比例函数定义中条件考虑不周全
【例1】若函数y=(m-2)是反比例函数,则m= .
本题容易由3-m2=-1解得答案为m=±2,此时,忽略了反比例函数中系数k的取值,导致解题出错,因此,解题时一定要考虑条件的周全,把握反比例函数的定义特点.
1.函数y=是y关于x的反比例函数,那么m的值是 .
反比例函数的图象与性质理解有误而致错
【例2】点M(x1,y1)和点N(x2,y2)在反比例函数y=(k为常数)的图象上,若x1<0<x2,求y1,y2,0的大小关系.
A(-3,y1),B(-1,y2),C(2,y3)三个点不在双曲线y=的同一个分支上,前两个点在第二象限内的分支上,第三个点在第四象限内的分支上,如图所示,显然第二象限内的分支上的所有点的纵坐标都大于第四象限内的分支上点的纵坐标,也就是说y随x的增大而增大是指在各自象限内而言的,不是笼统地概括.解题错误的原因就是没有将两个象限内的点分类讨论,而是一概而论.
2.(2024秋·宝安区校级期中)若点(-1,y1),(1,y2),(2,y3)在反比例函数y=(k<0)的图象上,则下列结论中正确的是( ).
A.y1>y2>y3 B.y1>y3>y2
C.y3>y1>y2 D.y3>y2>y1
反比例函数与一次函数的图象特征综合
【例3】在同一平面直角坐标系中,函数y=kx-k与y=的大致图象可能是( ).
A B C D
本题根据一次函数和反比例函数图象的特点进行分析选择,当k>0时,一次函数y=kx-k经过一、三、四象限,反比例函数的y=(k≠0)的图象的两个分支分别位于一、三象限,从而误选了A答案,此时忽略了一次函数中常数-k,因此,解题时,要注意符号及经过的象限.
3.(2024秋·南山区校级期中)已知一次函数y=kx+1(k≠0)与反比例函数y=(k≠0),则其图象可能是( ).
A B C D
反比例函数的定义理解
反比例函数的几种表示方式:xy=k或y=或y=kx-1,其中k是不等于零的常数.
1.反比例函数y=-中常数k为( ).
A.-5 B.2 C.- D.-
2.下列函数中,y是x的反比例函数的是( ).
A.y=3x B.y= C.y= D.y=+1
3.已知函数y=(k+2)是反比例函数,则k= .
反比例函数的图象和性质
若点(a,b)在反比例函数y=(k为常数,k≠0)的图象上,则点(-a,-b)也在此图象上,所以反比例函数的图象关于原点对称;在反比例函数y=(k为常数,k≠0) 中,由于x≠0且y≠0,所以两个分支都无限接近但永远不能达到x轴和y轴;反比例函数的增减性不是连续的,它的增减性都是在各自的象限内的增减情况,反比例函数的增减性都是由反比例系数k的符号决定的;反过来,由双曲线所在的位置和函数的增减性,也可以推断出k的符号.
4.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( ).
A.y1<y2<y3 B. y1<y3<y2 C. y3<y2<y1 D. y2<y1<y3
5.在如图所示的平面直角坐标系中,作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
(2)当2<y<4时,求x的取值范围;
(3)当-1<x<2,且x≠0时,求y的取值范围.
6.探究函数y=的图象与性质,小安根据学习函数的经验,对问题进行了探究.请补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)取几组y与x的对应值,填写在表中,其中m= ;
x … -7 -6 -4 -3 -1 0 2 3 …
y … 0.8 1 2 4 4 m 1 0.8 …
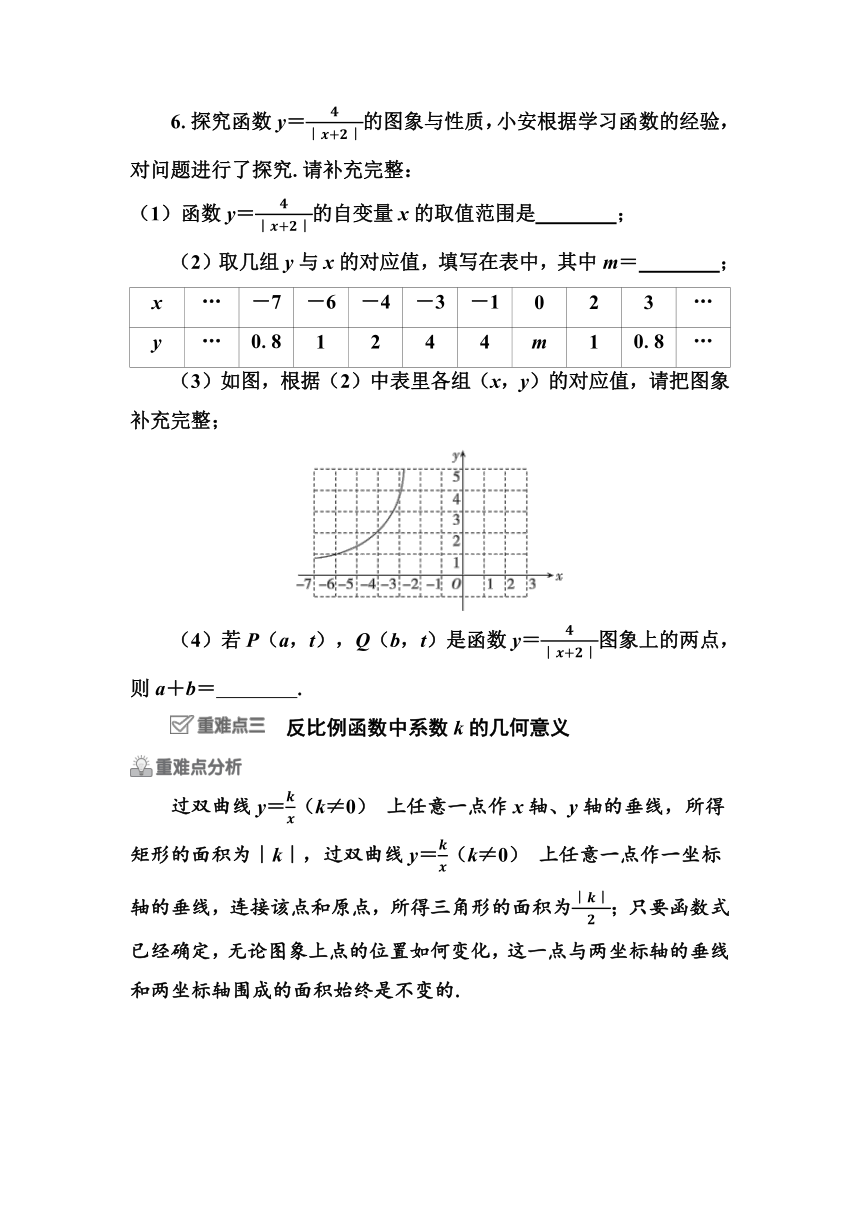
(3)如图,根据(2)中表里各组(x,y)的对应值,请把图象补充完整;
(4)若P(a,t),Q(b,t)是函数y=图象上的两点,则a+b= .
反比例函数中系数k的几何意义
过双曲线y=(k≠0) 上任意一点作x轴、y轴的垂线,所得矩形的面积为|k|,过双曲线y=(k≠0) 上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形的面积为;只要函数式已经确定,无论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.
7.如图,点A为反比例函数y=-(x<0)图象上的一点,连接AO,过点O作OA的垂线与反比例函数y=(x>0)的图象交于点B,则的值为 .
第7题图
8.矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数y=的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE.若四边形ODAF的面积为2,则k的值是 .
第8题图
反比例函数在生活中的实际应用
审清题意,根据常量、变量之间的关系,建立函数模型,设出函数表达式,待定系数用字母表示;列出方程,在实际问题中求出待定系数进而求得函数表达式,然后应用函数的图象和性质等知识解决问题.
9.(2024·福田区校级三模)在实验课上,小明做了一个实验.如图,在仪器左边托盘A(固定)中放置一个物体,在右边托盘B(可左右移动)中放置一个可以装水的容器,容器的质量为5 g.在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘B与点C的距离x(cm)(0<x≤60),记录容器中加入的水的质量,得到下表:
托盘B与点C的距离x/cm 30 25 20 15 10
容器与水的总质量y1/g 10 12 15 20 30
加入的水的质量y2/g 5 7 10 15 25
把表中的x与y1各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的y1关于x的函数图象.
(1)请在该平面直角坐标系中作出y2关于x的函数图象;
(2)观察函数图象,并结合表中的数据回答下列问题:
①直接写出y1关于x的函数表达式;
②当0<x≤60时,y1随x的增大而 (填“增大”或“减小”),y2随x的增大而 (填“增大”或“减小”);
③y2的图象与y1的图象有什么位置关系?
④求y2关于x的函数表达式;
(3)若在容器中加入的水的质量y2(g)满足19≤y2≤45,求托盘B与点C的距离x(cm)的取值范围.
10.(2023·深圳市高级中学期中)如图1,建筑是一门不断演化和创新的艺术,从古代的大理石殿堂到现代的钢铁森林,它的魅力在于其无限的可能性.近年来,一种名为双曲铝单板的新兴材料以其独特的曲线和光泽,为建筑注入了新的时尚元素,同时也赋予了建筑更多的创意和流动性.
图2为某广东厂家设计制造的双曲铝单板建筑的横截面,可以看成由两条曲线EG,FH(反比例函数图象的一支)和若干线段围成,其中四边形ABDC与四边形GMNH均为矩形,AB=2 m,BE=2 m,AC=20 m,GM=10 m,MN=4 m,取AC的中点O,以点O为原点,AC所在直线为x轴建立平面直角坐标系.
请回答下列问题:
(1)如图2,求EG所在双曲线的表达式;
(2)如图3,为在曲面实现自动化操作,工程师安装了支架EG,并加装了始终垂直于EG的伸缩机械臂PQ用来雕刻EG所在曲面的花纹,请问点P在EG上滑动时,PQ最长为多少米?
(3)如图4,为通风透气,避免潮湿,在某一时刻,打开遮光板AC,太阳光线经点A恰好照射到点E,请求出此时线段HN上光线无法直射部分的线段KN的长.
参考答案
【思维导图】
①反比例函数 ②零 ③列表 ④描点 ⑤曲线 ⑥中心对称图形 ⑦坐标原点 ⑧直线y=x ⑨直线y=-x
⑩ k>0 k<0 k>0 k<0
【易错点剖析】
【例1】-2 解析:∵y=(m-2)是反比例函数,∴3-m2=-1,m-2≠0,解得m=-2.
1.-2 解析:由题意,得|m|-1=1,m-2≠0,解得m=-2.
【例2】解:反比例函数y==中,(k-1)2+2>0,反比例函数图象分布在第一、三象限,
∵x1<0<x2,
∴点M在第三象限的图象上,点N在第一象限的图象上,
∴y1<0<y2.
2.B
【例3】C 解析:当k<0时,一次函数y=kx-k的图象经过第一、二、四象限,反比例函数y=(k≠0)的图象的两个分支分别在第二、四象限,故C选项的图象符合要求.
3.D 解析:当k>0时,可知y=kx+1(k≠0)的图象过第一、二三象限,y=(k≠0)的图象过第一、三象限;当k<0时,可知y=kx+1(k≠0)的图象过第一、二、四象限,y=(k≠0)的图象过第二、四象限,∴k<0与D选项中图象一致,故选D.
【重难点突破】
1.D 2.B
3.2 解析:∵函数y=(k+2)为反比例函数,∴k2-5=-1且k+2≠0,解得k=2.
4.D 解析:∵点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=的图象上,∴点A,B在第三象限,点C在第一象限,每个分支上y随x的增大而减小,∴y3>0,0>y1>y2,即y2<y1<y3.
5.解:作出图象的过程略.图略.
(1)当x=-2时,y==-3.
(2)当2<y<4时,<x<3.
(3)当-1<x<2,且x≠0时,y<-6或y>3.
6.解:(1)由题意得,函数y=的自变量x的取值范围是x+2≠0,即x≠-2,故答案为x≠-2.
(2)在y=中,当x=0时,y===2,
∴m=2,故答案为2.
解:(3)如图所示,即为所求.
(4)由函数图象可知,函数y=的图象关于直线x=-2对称.
∵P(a,t),Q(b,t)是函数y=图象上的两点,
∴P,Q关于直线x=-2对称,
∴=-2,∴a+b=-4.故答案为-4.
7. 解析:如图,作AG⊥x轴,垂足为G,作BH⊥x轴,垂足为H,
∵点A在反比例函数y=-的图象上,点B在反比例函数y=的图象上,∴S△AGO=,S△BOH=2.
∵∠AOB=90°,∴∠AOG=∠HBO.
又∵∠AGO=∠OHB,∴△AGO∽△OHB,
∴=()2=,∴=.
8. 解析:如图,过点E作EM⊥OC,则EM∥OB,
∴△OME∽△OCA,∴==.
设E(a,),
∵OE=2AE,∴==,
∴OC=a,AC=·,
∴S矩形OBAC=S△OBD+S△OCF+S四边形ODAF=a··,
即++2=a··,解得k=.
9.解:(1)y2关于x的函数图象如图所示.
解:(2)①由表格可知,xy1=300,即y1=,
∴y1关于x的函数表达式为y1=(0<x≤60).
解:②观察图象可知,当0<x≤60时,y1随x的增大而减小,y2随x的增大而减小.
故答案为:减小,减小.
解:③由图象可知,将y1的图象向下平移得到y2的图象.
解:④由表格可知,x(y2+5)=300,即y2=-5,
∴y2关于x的函数表达式为y2=-5.
解:(3)当19≤y2≤45时,得19≤-5≤45,解得6≤x≤12.5,
∴托盘B与点C的距离x(cm)的取值范围是6≤x≤12.5.
10.解:(1)∵AC=20 m.∵O为AC的中点,∴AO=10 m.∴E(-8,-2),设EG所在双曲线的表达式为y=,将点E的坐标(-8,-2)代入表达式中,得-2=,解得k=16,∴抛物线的表达式为y=.
解:(2)根据题意得点E与点G的坐标分别为(-8,-2),(-2,-8),
设EG所在直线的表达式为y=k1x+b1,将E,G两点坐标代入得解得
∴EG所在直线的表达式为y=-x-10.
曲线EG关于直线y=x轴对称,
联立解得∴P(-5,-5),
联立解得(舍去)或
∴Q(-4,-4),
∴PQmax==.
(3)如图,光线与曲线EG只有一个交点T,
设直线AE的表达式为y=kx+b,将点A(-10,0),点E(-8,-2)的坐标代入得
解得
∴直线AE的表达式为y=-x-10.
∵TK∥AE,∴可设直线TK的表达式为y=-x+m.
联立得
整理得-x2+mx-16=0,∴Δ=m2-64=0,
解得m=-8或m=8(舍去),
∴直线TK的表达式为y=-x-8,
将x=2代入y=-x-8,
得y=-2-8=-10,∴点K(2,-10).
∵点H(2,-8),∴点H(-2,-8),∴点N(2,-18),
∴KN=8.
. . . . . . . . .
反比例函数定义中条件考虑不周全
【例1】若函数y=(m-2)是反比例函数,则m= .
本题容易由3-m2=-1解得答案为m=±2,此时,忽略了反比例函数中系数k的取值,导致解题出错,因此,解题时一定要考虑条件的周全,把握反比例函数的定义特点.
1.函数y=是y关于x的反比例函数,那么m的值是 .
反比例函数的图象与性质理解有误而致错
【例2】点M(x1,y1)和点N(x2,y2)在反比例函数y=(k为常数)的图象上,若x1<0<x2,求y1,y2,0的大小关系.
A(-3,y1),B(-1,y2),C(2,y3)三个点不在双曲线y=的同一个分支上,前两个点在第二象限内的分支上,第三个点在第四象限内的分支上,如图所示,显然第二象限内的分支上的所有点的纵坐标都大于第四象限内的分支上点的纵坐标,也就是说y随x的增大而增大是指在各自象限内而言的,不是笼统地概括.解题错误的原因就是没有将两个象限内的点分类讨论,而是一概而论.
2.(2024秋·宝安区校级期中)若点(-1,y1),(1,y2),(2,y3)在反比例函数y=(k<0)的图象上,则下列结论中正确的是( ).
A.y1>y2>y3 B.y1>y3>y2
C.y3>y1>y2 D.y3>y2>y1
反比例函数与一次函数的图象特征综合
【例3】在同一平面直角坐标系中,函数y=kx-k与y=的大致图象可能是( ).
A B C D
本题根据一次函数和反比例函数图象的特点进行分析选择,当k>0时,一次函数y=kx-k经过一、三、四象限,反比例函数的y=(k≠0)的图象的两个分支分别位于一、三象限,从而误选了A答案,此时忽略了一次函数中常数-k,因此,解题时,要注意符号及经过的象限.
3.(2024秋·南山区校级期中)已知一次函数y=kx+1(k≠0)与反比例函数y=(k≠0),则其图象可能是( ).
A B C D
反比例函数的定义理解
反比例函数的几种表示方式:xy=k或y=或y=kx-1,其中k是不等于零的常数.
1.反比例函数y=-中常数k为( ).
A.-5 B.2 C.- D.-
2.下列函数中,y是x的反比例函数的是( ).
A.y=3x B.y= C.y= D.y=+1
3.已知函数y=(k+2)是反比例函数,则k= .
反比例函数的图象和性质
若点(a,b)在反比例函数y=(k为常数,k≠0)的图象上,则点(-a,-b)也在此图象上,所以反比例函数的图象关于原点对称;在反比例函数y=(k为常数,k≠0) 中,由于x≠0且y≠0,所以两个分支都无限接近但永远不能达到x轴和y轴;反比例函数的增减性不是连续的,它的增减性都是在各自的象限内的增减情况,反比例函数的增减性都是由反比例系数k的符号决定的;反过来,由双曲线所在的位置和函数的增减性,也可以推断出k的符号.
4.若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( ).
A.y1<y2<y3 B. y1<y3<y2 C. y3<y2<y1 D. y2<y1<y3
5.在如图所示的平面直角坐标系中,作出函数y=的图象,并根据图象回答下列问题:
(1)当x=-2时,求y的值;
(2)当2<y<4时,求x的取值范围;
(3)当-1<x<2,且x≠0时,求y的取值范围.
6.探究函数y=的图象与性质,小安根据学习函数的经验,对问题进行了探究.请补充完整:
(1)函数y=的自变量x的取值范围是 ;
(2)取几组y与x的对应值,填写在表中,其中m= ;
x … -7 -6 -4 -3 -1 0 2 3 …
y … 0.8 1 2 4 4 m 1 0.8 …
(3)如图,根据(2)中表里各组(x,y)的对应值,请把图象补充完整;
(4)若P(a,t),Q(b,t)是函数y=图象上的两点,则a+b= .
反比例函数中系数k的几何意义
过双曲线y=(k≠0) 上任意一点作x轴、y轴的垂线,所得矩形的面积为|k|,过双曲线y=(k≠0) 上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形的面积为;只要函数式已经确定,无论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.
7.如图,点A为反比例函数y=-(x<0)图象上的一点,连接AO,过点O作OA的垂线与反比例函数y=(x>0)的图象交于点B,则的值为 .
第7题图
8.矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数y=的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE.若四边形ODAF的面积为2,则k的值是 .
第8题图
反比例函数在生活中的实际应用
审清题意,根据常量、变量之间的关系,建立函数模型,设出函数表达式,待定系数用字母表示;列出方程,在实际问题中求出待定系数进而求得函数表达式,然后应用函数的图象和性质等知识解决问题.
9.(2024·福田区校级三模)在实验课上,小明做了一个实验.如图,在仪器左边托盘A(固定)中放置一个物体,在右边托盘B(可左右移动)中放置一个可以装水的容器,容器的质量为5 g.在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘B与点C的距离x(cm)(0<x≤60),记录容器中加入的水的质量,得到下表:
托盘B与点C的距离x/cm 30 25 20 15 10
容器与水的总质量y1/g 10 12 15 20 30
加入的水的质量y2/g 5 7 10 15 25
把表中的x与y1各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的y1关于x的函数图象.
(1)请在该平面直角坐标系中作出y2关于x的函数图象;
(2)观察函数图象,并结合表中的数据回答下列问题:
①直接写出y1关于x的函数表达式;
②当0<x≤60时,y1随x的增大而 (填“增大”或“减小”),y2随x的增大而 (填“增大”或“减小”);
③y2的图象与y1的图象有什么位置关系?
④求y2关于x的函数表达式;
(3)若在容器中加入的水的质量y2(g)满足19≤y2≤45,求托盘B与点C的距离x(cm)的取值范围.
10.(2023·深圳市高级中学期中)如图1,建筑是一门不断演化和创新的艺术,从古代的大理石殿堂到现代的钢铁森林,它的魅力在于其无限的可能性.近年来,一种名为双曲铝单板的新兴材料以其独特的曲线和光泽,为建筑注入了新的时尚元素,同时也赋予了建筑更多的创意和流动性.
图2为某广东厂家设计制造的双曲铝单板建筑的横截面,可以看成由两条曲线EG,FH(反比例函数图象的一支)和若干线段围成,其中四边形ABDC与四边形GMNH均为矩形,AB=2 m,BE=2 m,AC=20 m,GM=10 m,MN=4 m,取AC的中点O,以点O为原点,AC所在直线为x轴建立平面直角坐标系.
请回答下列问题:
(1)如图2,求EG所在双曲线的表达式;
(2)如图3,为在曲面实现自动化操作,工程师安装了支架EG,并加装了始终垂直于EG的伸缩机械臂PQ用来雕刻EG所在曲面的花纹,请问点P在EG上滑动时,PQ最长为多少米?
(3)如图4,为通风透气,避免潮湿,在某一时刻,打开遮光板AC,太阳光线经点A恰好照射到点E,请求出此时线段HN上光线无法直射部分的线段KN的长.
参考答案
【思维导图】
①反比例函数 ②零 ③列表 ④描点 ⑤曲线 ⑥中心对称图形 ⑦坐标原点 ⑧直线y=x ⑨直线y=-x
⑩ k>0 k<0 k>0 k<0
【易错点剖析】
【例1】-2 解析:∵y=(m-2)是反比例函数,∴3-m2=-1,m-2≠0,解得m=-2.
1.-2 解析:由题意,得|m|-1=1,m-2≠0,解得m=-2.
【例2】解:反比例函数y==中,(k-1)2+2>0,反比例函数图象分布在第一、三象限,
∵x1<0<x2,
∴点M在第三象限的图象上,点N在第一象限的图象上,
∴y1<0<y2.
2.B
【例3】C 解析:当k<0时,一次函数y=kx-k的图象经过第一、二、四象限,反比例函数y=(k≠0)的图象的两个分支分别在第二、四象限,故C选项的图象符合要求.
3.D 解析:当k>0时,可知y=kx+1(k≠0)的图象过第一、二三象限,y=(k≠0)的图象过第一、三象限;当k<0时,可知y=kx+1(k≠0)的图象过第一、二、四象限,y=(k≠0)的图象过第二、四象限,∴k<0与D选项中图象一致,故选D.
【重难点突破】
1.D 2.B
3.2 解析:∵函数y=(k+2)为反比例函数,∴k2-5=-1且k+2≠0,解得k=2.
4.D 解析:∵点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数y=的图象上,∴点A,B在第三象限,点C在第一象限,每个分支上y随x的增大而减小,∴y3>0,0>y1>y2,即y2<y1<y3.
5.解:作出图象的过程略.图略.
(1)当x=-2时,y==-3.
(2)当2<y<4时,<x<3.
(3)当-1<x<2,且x≠0时,y<-6或y>3.
6.解:(1)由题意得,函数y=的自变量x的取值范围是x+2≠0,即x≠-2,故答案为x≠-2.
(2)在y=中,当x=0时,y===2,
∴m=2,故答案为2.
解:(3)如图所示,即为所求.
(4)由函数图象可知,函数y=的图象关于直线x=-2对称.
∵P(a,t),Q(b,t)是函数y=图象上的两点,
∴P,Q关于直线x=-2对称,
∴=-2,∴a+b=-4.故答案为-4.
7. 解析:如图,作AG⊥x轴,垂足为G,作BH⊥x轴,垂足为H,
∵点A在反比例函数y=-的图象上,点B在反比例函数y=的图象上,∴S△AGO=,S△BOH=2.
∵∠AOB=90°,∴∠AOG=∠HBO.
又∵∠AGO=∠OHB,∴△AGO∽△OHB,
∴=()2=,∴=.
8. 解析:如图,过点E作EM⊥OC,则EM∥OB,
∴△OME∽△OCA,∴==.
设E(a,),
∵OE=2AE,∴==,
∴OC=a,AC=·,
∴S矩形OBAC=S△OBD+S△OCF+S四边形ODAF=a··,
即++2=a··,解得k=.
9.解:(1)y2关于x的函数图象如图所示.
解:(2)①由表格可知,xy1=300,即y1=,
∴y1关于x的函数表达式为y1=(0<x≤60).
解:②观察图象可知,当0<x≤60时,y1随x的增大而减小,y2随x的增大而减小.
故答案为:减小,减小.
解:③由图象可知,将y1的图象向下平移得到y2的图象.
解:④由表格可知,x(y2+5)=300,即y2=-5,
∴y2关于x的函数表达式为y2=-5.
解:(3)当19≤y2≤45时,得19≤-5≤45,解得6≤x≤12.5,
∴托盘B与点C的距离x(cm)的取值范围是6≤x≤12.5.
10.解:(1)∵AC=20 m.∵O为AC的中点,∴AO=10 m.∴E(-8,-2),设EG所在双曲线的表达式为y=,将点E的坐标(-8,-2)代入表达式中,得-2=,解得k=16,∴抛物线的表达式为y=.
解:(2)根据题意得点E与点G的坐标分别为(-8,-2),(-2,-8),
设EG所在直线的表达式为y=k1x+b1,将E,G两点坐标代入得解得
∴EG所在直线的表达式为y=-x-10.
曲线EG关于直线y=x轴对称,
联立解得∴P(-5,-5),
联立解得(舍去)或
∴Q(-4,-4),
∴PQmax==.
(3)如图,光线与曲线EG只有一个交点T,
设直线AE的表达式为y=kx+b,将点A(-10,0),点E(-8,-2)的坐标代入得
解得
∴直线AE的表达式为y=-x-10.
∵TK∥AE,∴可设直线TK的表达式为y=-x+m.
联立得
整理得-x2+mx-16=0,∴Δ=m2-64=0,
解得m=-8或m=8(舍去),
∴直线TK的表达式为y=-x-8,
将x=2代入y=-x-8,
得y=-2-8=-10,∴点K(2,-10).
∵点H(2,-8),∴点H(-2,-8),∴点N(2,-18),
∴KN=8.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
