第三章概率的进一步认识 重难点分类练(含答案)2025-2026学年数学北师大版九年级上册
文档属性
| 名称 | 第三章概率的进一步认识 重难点分类练(含答案)2025-2026学年数学北师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 474.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 21:48:42 | ||
图片预览



文档简介
第三章 概率的进一步认识
. . . . .
忽略“放回”与“不放回”而出错
【例1】(2023·佛山九年级练习)将分别标有“大”“美”“明”“德”四个汉字的小球装在一个不透明的口袋中,这些小球除汉字以外其他完全相同,每次摸球前先搅匀,随机摸出一球,不放回,再随机摸出一球,两次摸出的球上的汉字可以组成“明德”的概率是( ).
A. B. C. D.
1.“放回”抽取问题,第一次抽取后又放回,第二次抽取不受第一次的影响;
2.“不放回”抽取问题中第一次抽取到的元素,第二次就抽取不到.
1.(2023·梅州二模)桌面上有5本书,2本为数学书,2本为物理书,1本为化学书,小明分2次从桌上抽走2本书,则小明2次抽走的都是数学书的概率为( ).
A. B. C. D.
2.在一个不透明的袋中装着2个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为 .
不能正确理解频率与概率的关系而出错
【例2】(2023·深圳九年级期中)已知抛一枚均匀硬币正面朝上的概率为,下列说法中正确的是( ).
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币10次都不可能正面朝上
C.连续抛一枚均匀硬币100次一定出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
(1)试验中,某事件发生的次数与总次数的比值,称为频率;
(2)随着试验次数的增加,这个事件发生的频率呈现出稳定性,逐渐稳定于某一数值,可以用这一事件发生的频率估计这个事件发生的概率.试验得出的频率只是概率的近似值.
3.(2024秋·宝安区校级期中)某射击运动员在同一条件下的射击成绩记录如下表:
射击次数 100 200 400 800 1 000
“射中九环以上”的次数 87 172 336 679 850
“射中九环以上”的频率 0.87 0.86 0.84 0.85 0.85
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( ).
A.0.84 B.0.85 C.0.86 D.0.87
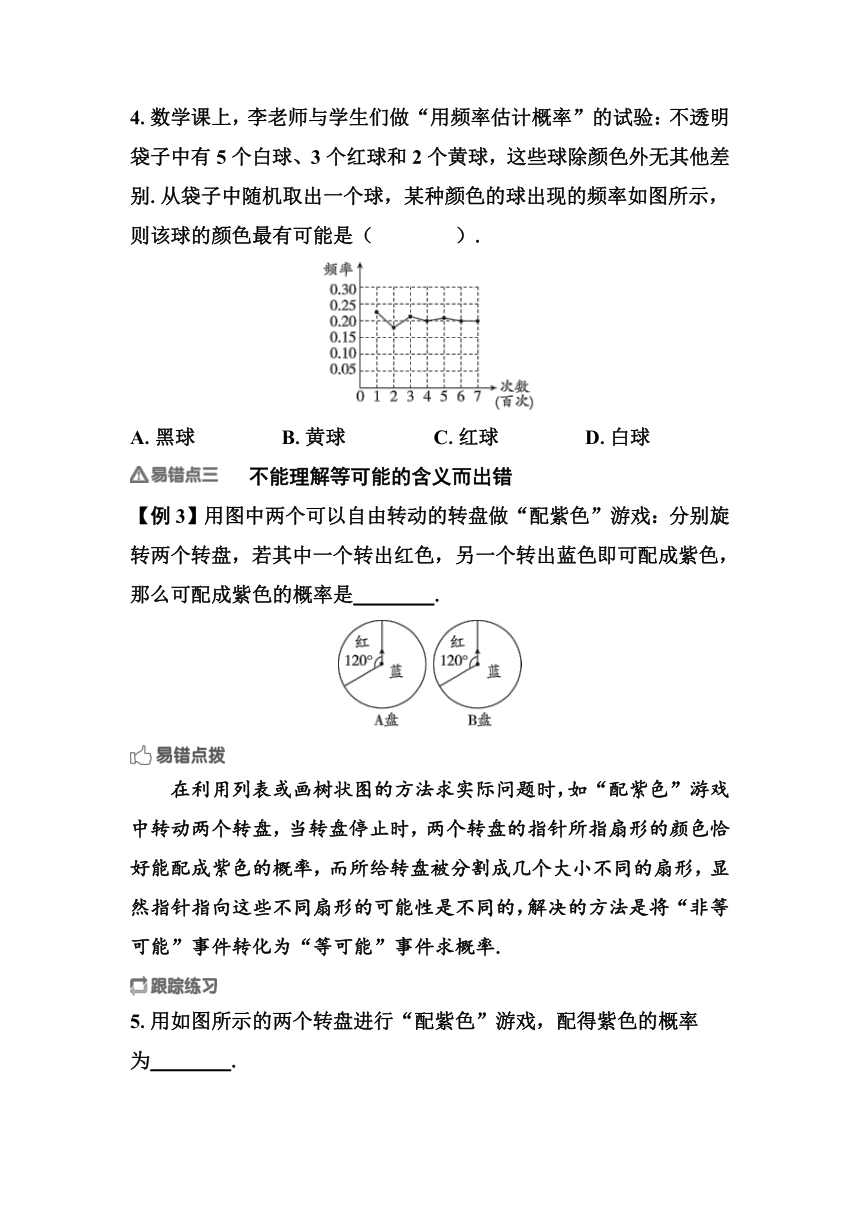
4.数学课上,李老师与学生们做“用频率估计概率”的试验:不透明袋子中有5个白球、3个红球和2个黄球,这些球除颜色外无其他差别.从袋子中随机取出一个球,某种颜色的球出现的频率如图所示,则该球的颜色最有可能是( ).
A.黑球 B.黄球 C.红球 D.白球
不能理解等可能的含义而出错
【例3】用图中两个可以自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是 .
在利用列表或画树状图的方法求实际问题时,如“配紫色”游戏中转动两个转盘,当转盘停止时,两个转盘的指针所指扇形的颜色恰好能配成紫色的概率,而所给转盘被分割成几个大小不同的扇形,显然指针指向这些不同扇形的可能性是不同的,解决的方法是将“非等可能”事件转化为“等可能”事件求概率.
5.用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率为 .
6.某中学联谊会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小亮同学同时转动A盘和B盘,他赢得游戏的概率是 .
利用树状图或表格求概率
1.利用树状图或表格可以不重复、不遗漏地列出所有可能的结果,从而比较方便地求出某些事件发生的概率.
2.在摸球游戏中,“有放回”与“无放回”直接影响第二次等可能的结果,“有放回”包含放回的这个球;“无放回”则不包含这个球.需注意“一次拿两个球”与“无放回”是同一种类型.
1.从甲、乙、丙、丁4名同学中随机抽取2名同学参加图书节志愿服务活动,其中甲同学是女生,乙、丙、丁同学都是男生,则被抽到的2名同学都是男生的概率为( ).
A. B. C. D.
2.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“立春”“立夏”“秋分”“大寒”四张邮票中抽取两张,则恰好抽到“立夏”“秋分”两张邮票的概率是( ).
A. B. C. D.
3.(2024秋·福田区期末)如图,电路图上有三个开关S1,S2,S3,和两个小灯泡L1,L2,随机闭合开关S1,S2,S3中的两个,能让灯泡L2发光的概率是 .
4.(2025·深圳模拟)某校开展以“新时代深圳精神”为主题的演讲比赛.“新时代深圳精神”概括凝结为16个字:“敢闯敢试、开放包容、务实尚法、追求卓越.”这四个主题依次用字母A,B,C,D表示.将A,B,C,D分别写在四张完全相同的不透明卡片上,然后背面朝上洗匀.每位选手随机从中抽出一张卡片,并按照抽到的主题进行演讲.
(1)小明抽到演讲主题为“追求卓越”的概率是 ;
(2)小颖从中抽出一张卡片,记下字母后放回.重新洗匀后,小亮再从中抽出一张卡片,求他们演讲主题相同的概率.
用频率估计概率
事件的概率是一个确定的常数,而频率是不确定的,当试验次数较少时,频率的大小摇摆不定,当试验次数增大时,频率的大小波动变小,并逐渐稳定在概率附近.可见,概率是频率的稳定值,而频率是概率的近似值.
5.一辆汽车经过某十字路口,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则直行经过这个十字路口的概率为 .
6.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.7左右,则布袋中白球可能有 个.
7.(2024秋·龙岗区校级月考)如图①,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5 m,宽为4 m的矩形将不规则图案围起来,然后在适当位置随机地朝矩形区域内扔小球,并记录小球落在不规则图案内的次数,将若干次有效试验的结果绘制成了如图②所示的折线统计图.若每次投掷,小球落在矩形内每个点的可能性相同,由此他可以估计不规则图案的面积为 m2.
8.在学习《用频率估计概率》这一节课后,数学兴趣小组设计了摸球试验:在一个不透明的盒子里装有质地大小都相同的红球和黑球共4个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,如表是他们整理得到的试验数据:
摸球的次数n 500 1 000 2 000 2 500 3 000 6 000
摸到红球的次数m 351 722 1 486 1 870 2 262 4 512
摸到红球的频率 0.702 0.722 0.743 0.748 0.754 0.752
(1)请估计:当n=10 000时,摸到红球的频率将会接近 ;(精确到0.01)
(2)试估计:盒子中有红球 个;
(3)请画树状图或列表计算:从口袋中先摸出1个球,不放回,再摸出1个球,求摸出的两个球都是红球的概率.
参考答案
【思维导图】
①不重复 ②不遗漏 ③概率 ④相同 ⑤比值 ⑥概率
【易错点剖析】
【例1】A 1.A 2.
【例2】D 3.B 4.B
【例3】 5. 6.
【重难点突破】
1.B 2.C 3.
4.解:(1)小明抽到演讲主题为“追求卓越”的概率是,
故答案为.
解:(2)由题意,列表为:
A B C D
A (A,A) (B,A) (C,A) (D,A)
B (A,B) (B,B) (C,B) (D,B)
C (A,C) (B,C) (C,C) (D,C)
D (A,D) (B,D) (C,D) (D,D)
共有16种等可能的结果,他们演讲主题相同的有4种结果,
所以他们演讲主题相同的概率为=.
5. 6.15 7.7
8.解:(1)由题表可知随着试验次数的增加,摸到红球的频率稳定在0.75左右,所以可估计当n=10 000时,摸到红球的频率将会接近0.75,故答案为0.75.
解:(2)由表格中摸到红球的频率可得,红球个数约为4×0.75=3,
故答案为3.
解:(3)列表:设红球为A1,A2,A3,黑球为B.
二 一 A1 A2 A3 B
A1 (A1,A2) (A1,A3) (A1,B)
A2 (A2,A1) (A2,A3) (A2,B)
A3 (A3,A1) (A3,A2) (A3,B)
B (B,A1) (B,A2) (B,A3)
一共有12种等可能的结果.
两次都摸到红球的结果有6种,
∴P(两次都摸到红球)==.
. . . . .
忽略“放回”与“不放回”而出错
【例1】(2023·佛山九年级练习)将分别标有“大”“美”“明”“德”四个汉字的小球装在一个不透明的口袋中,这些小球除汉字以外其他完全相同,每次摸球前先搅匀,随机摸出一球,不放回,再随机摸出一球,两次摸出的球上的汉字可以组成“明德”的概率是( ).
A. B. C. D.
1.“放回”抽取问题,第一次抽取后又放回,第二次抽取不受第一次的影响;
2.“不放回”抽取问题中第一次抽取到的元素,第二次就抽取不到.
1.(2023·梅州二模)桌面上有5本书,2本为数学书,2本为物理书,1本为化学书,小明分2次从桌上抽走2本书,则小明2次抽走的都是数学书的概率为( ).
A. B. C. D.
2.在一个不透明的袋中装着2个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为 .
不能正确理解频率与概率的关系而出错
【例2】(2023·深圳九年级期中)已知抛一枚均匀硬币正面朝上的概率为,下列说法中正确的是( ).
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币10次都不可能正面朝上
C.连续抛一枚均匀硬币100次一定出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
(1)试验中,某事件发生的次数与总次数的比值,称为频率;
(2)随着试验次数的增加,这个事件发生的频率呈现出稳定性,逐渐稳定于某一数值,可以用这一事件发生的频率估计这个事件发生的概率.试验得出的频率只是概率的近似值.
3.(2024秋·宝安区校级期中)某射击运动员在同一条件下的射击成绩记录如下表:
射击次数 100 200 400 800 1 000
“射中九环以上”的次数 87 172 336 679 850
“射中九环以上”的频率 0.87 0.86 0.84 0.85 0.85
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( ).
A.0.84 B.0.85 C.0.86 D.0.87
4.数学课上,李老师与学生们做“用频率估计概率”的试验:不透明袋子中有5个白球、3个红球和2个黄球,这些球除颜色外无其他差别.从袋子中随机取出一个球,某种颜色的球出现的频率如图所示,则该球的颜色最有可能是( ).
A.黑球 B.黄球 C.红球 D.白球
不能理解等可能的含义而出错
【例3】用图中两个可以自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是 .
在利用列表或画树状图的方法求实际问题时,如“配紫色”游戏中转动两个转盘,当转盘停止时,两个转盘的指针所指扇形的颜色恰好能配成紫色的概率,而所给转盘被分割成几个大小不同的扇形,显然指针指向这些不同扇形的可能性是不同的,解决的方法是将“非等可能”事件转化为“等可能”事件求概率.
5.用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率为 .
6.某中学联谊会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,A盘被分成面积相等的几个扇形,B盘中蓝色扇形区域的圆心角是120°.同学们同时转动两个转盘,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,那么可以配成紫色,赢得游戏.若小亮同学同时转动A盘和B盘,他赢得游戏的概率是 .
利用树状图或表格求概率
1.利用树状图或表格可以不重复、不遗漏地列出所有可能的结果,从而比较方便地求出某些事件发生的概率.
2.在摸球游戏中,“有放回”与“无放回”直接影响第二次等可能的结果,“有放回”包含放回的这个球;“无放回”则不包含这个球.需注意“一次拿两个球”与“无放回”是同一种类型.
1.从甲、乙、丙、丁4名同学中随机抽取2名同学参加图书节志愿服务活动,其中甲同学是女生,乙、丙、丁同学都是男生,则被抽到的2名同学都是男生的概率为( ).
A. B. C. D.
2.“二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“立春”“立夏”“秋分”“大寒”四张邮票中抽取两张,则恰好抽到“立夏”“秋分”两张邮票的概率是( ).
A. B. C. D.
3.(2024秋·福田区期末)如图,电路图上有三个开关S1,S2,S3,和两个小灯泡L1,L2,随机闭合开关S1,S2,S3中的两个,能让灯泡L2发光的概率是 .
4.(2025·深圳模拟)某校开展以“新时代深圳精神”为主题的演讲比赛.“新时代深圳精神”概括凝结为16个字:“敢闯敢试、开放包容、务实尚法、追求卓越.”这四个主题依次用字母A,B,C,D表示.将A,B,C,D分别写在四张完全相同的不透明卡片上,然后背面朝上洗匀.每位选手随机从中抽出一张卡片,并按照抽到的主题进行演讲.
(1)小明抽到演讲主题为“追求卓越”的概率是 ;
(2)小颖从中抽出一张卡片,记下字母后放回.重新洗匀后,小亮再从中抽出一张卡片,求他们演讲主题相同的概率.
用频率估计概率
事件的概率是一个确定的常数,而频率是不确定的,当试验次数较少时,频率的大小摇摆不定,当试验次数增大时,频率的大小波动变小,并逐渐稳定在概率附近.可见,概率是频率的稳定值,而频率是概率的近似值.
5.一辆汽车经过某十字路口,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则直行经过这个十字路口的概率为 .
6.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.7左右,则布袋中白球可能有 个.
7.(2024秋·龙岗区校级月考)如图①,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5 m,宽为4 m的矩形将不规则图案围起来,然后在适当位置随机地朝矩形区域内扔小球,并记录小球落在不规则图案内的次数,将若干次有效试验的结果绘制成了如图②所示的折线统计图.若每次投掷,小球落在矩形内每个点的可能性相同,由此他可以估计不规则图案的面积为 m2.
8.在学习《用频率估计概率》这一节课后,数学兴趣小组设计了摸球试验:在一个不透明的盒子里装有质地大小都相同的红球和黑球共4个,将球搅匀后从中随机摸出一个记下颜色,放回,再重复进行下一次试验,如表是他们整理得到的试验数据:
摸球的次数n 500 1 000 2 000 2 500 3 000 6 000
摸到红球的次数m 351 722 1 486 1 870 2 262 4 512
摸到红球的频率 0.702 0.722 0.743 0.748 0.754 0.752
(1)请估计:当n=10 000时,摸到红球的频率将会接近 ;(精确到0.01)
(2)试估计:盒子中有红球 个;
(3)请画树状图或列表计算:从口袋中先摸出1个球,不放回,再摸出1个球,求摸出的两个球都是红球的概率.
参考答案
【思维导图】
①不重复 ②不遗漏 ③概率 ④相同 ⑤比值 ⑥概率
【易错点剖析】
【例1】A 1.A 2.
【例2】D 3.B 4.B
【例3】 5. 6.
【重难点突破】
1.B 2.C 3.
4.解:(1)小明抽到演讲主题为“追求卓越”的概率是,
故答案为.
解:(2)由题意,列表为:
A B C D
A (A,A) (B,A) (C,A) (D,A)
B (A,B) (B,B) (C,B) (D,B)
C (A,C) (B,C) (C,C) (D,C)
D (A,D) (B,D) (C,D) (D,D)
共有16种等可能的结果,他们演讲主题相同的有4种结果,
所以他们演讲主题相同的概率为=.
5. 6.15 7.7
8.解:(1)由题表可知随着试验次数的增加,摸到红球的频率稳定在0.75左右,所以可估计当n=10 000时,摸到红球的频率将会接近0.75,故答案为0.75.
解:(2)由表格中摸到红球的频率可得,红球个数约为4×0.75=3,
故答案为3.
解:(3)列表:设红球为A1,A2,A3,黑球为B.
二 一 A1 A2 A3 B
A1 (A1,A2) (A1,A3) (A1,B)
A2 (A2,A1) (A2,A3) (A2,B)
A3 (A3,A1) (A3,A2) (A3,B)
B (B,A1) (B,A2) (B,A3)
一共有12种等可能的结果.
两次都摸到红球的结果有6种,
∴P(两次都摸到红球)==.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
