期末复习(四) 图形的相似 考点分类练(含答案) 2025-2026学年数学北师大版九年级上册
文档属性
| 名称 | 期末复习(四) 图形的相似 考点分类练(含答案) 2025-2026学年数学北师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 21:54:47 | ||
图片预览



文档简介
期末复习(四) 图形的相似
一、考点过关
考点1 比例性质
1.若=,则=( ).
A. B.- C.7 D.-7
考点2 平行线分线段成比例基本事实及其推论基本应用
2.如图,在△ABC中,点D在边AB上,过点D作DE∥BC,交AC于点E.若AD=2,BD=3,则的值是( ).
A. B. C. D.
考点3 黄金分割点
3.如图,若点D是线段AB的黄金分割点(AD>BD),AB=4,则AD的长是( ).
A.3 B.6-2 C.2-2 D.2-1
考点4 相似图形及其性质
4.如图,四边形ABCD和四边形EFGH相似,且顶点都在方格纸的格点上,它们的相似比是( ).
A.1∶2 B.1∶4 C.2∶1 D.4∶1
考点5 两三角形相似的判定及性质
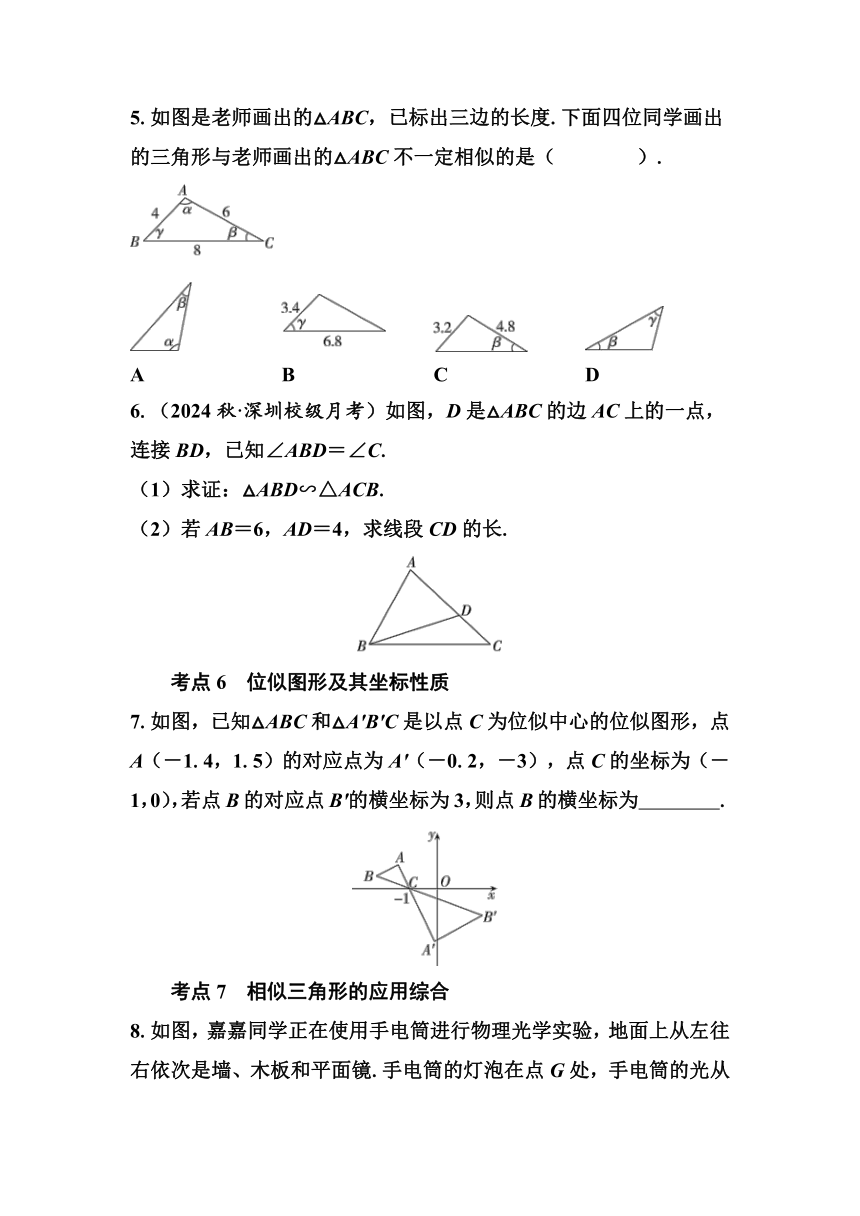
5.如图是老师画出的△ABC,已标出三边的长度.下面四位同学画出的三角形与老师画出的△ABC不一定相似的是( ).
A B C D
6.(2024秋·深圳校级月考)如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C.
(1)求证:△ABD∽△ACB.
(2)若AB=6,AD=4,求线段CD的长.
考点6 位似图形及其坐标性质
7.如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,点A(-1.4,1.5)的对应点为A'(-0.2,-3),点C的坐标为(-1,0),若点B的对应点B'的横坐标为3,则点B的横坐标为 .
考点7 相似三角形的应用综合
8.如图,嘉嘉同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度DE=3.5 m,点F到地面的高度CF=1.5 m,灯泡到木板的水平距离AC=5.4 m,墙到木板的水平距离为CD=4 m.已知光在镜面反射中的入射角等于反射角,图中点A,B,C,D在同一水平面上.求灯泡到地面的高度AG.
二、核心考题
9.如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC的面积比是1∶4,若AB=6,则CD的长为 .
第9题图
10.如图,Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为D,AE平分∠BAC,分别交BD,BC于点F,E.若AB∶BC=3∶4,则BF∶FD为( ).
第10题图
A.5∶3 B.5∶4 C.4∶3 D.2∶1
11.某数学兴趣小组决定利用所学知识测量一古建筑(如图1)的高度.如图2,古建筑的高度为AB,在地面BC上取E,G两点,分别竖立两根高为1.5 m的标杆EF和GH,两标杆间隔EG为26 m,并且古建筑AB、标杆EF和GH在同一竖直平面内.从标杆EF后退2 m到D处(即ED=2 m),从D处观察点A,A,F,D在同一直线上;从标杆GH后退4 m到C处(即CG=4 m),从C处观察点A,A,H,C三点也在同一直线上.已知点B,E,D,G,C在同一直线上,AB⊥BC,EF⊥BC,GH⊥BC,请你根据以上测量数据,帮助数学兴趣小组求出该古建筑AB的高度.
12.如图,在矩形ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点E.
(1)求证:△ABM∽△EMA;
(2)若AB=4,BM=3,求ME的长.
三、提升考题
13.如图,在平面直角坐标系中, ABCD的边AD=6,若OA,OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
(1)求OA,OB的长;
(2)若x轴上有一个点E满足S△AOE=,求证:△AOE∽△DAO.
14.如图,在6×6的正方形网格中,每个小正方形的边长均相等,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)如图1,以点O为位似中心画△ODE,使得△ODE与△OAB位似,且相似比为2∶1,D,E为格点.
(2)如图2,在OA边上找一点F,使得=.
参考答案
1.B 2.A 3.C 4.C 5.C
6.解:(1)在△ABD和△ACB中,∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB.
(2)∵△ABD∽△ACB,∴=.
∵AB=6,AD=4,∴AC===9,
则CD=AC-AD=9-4=5.
7.-3 解析:过点A作AM⊥x轴于点M,过A'作A'N⊥x轴于点N(图略),则AM∥A'N,∴△ACM∽△A'CN,∴=.∵点A(-1.4,1.5)的对应点为A'(-0.2,-3),点C的坐标为(-1,0),∴===,∴△ABC和△A'B'C的相似比为1∶2.过点B作BE⊥x轴作于点E,过点B'作B'F⊥x轴于点F,则BE∥B'F,∴△BCE∽△B'CF,∴=,∵点C的坐标为(-1,0),点B'的横坐标为3,∴CF=4,∵△ABC和△A'B'C的相似比为1∶2,即=,∴=,解得EC=2,∴点B的横坐标为-3.
8.解:由题意可得FC∥DE,则
△BFC∽△BED,故=,
即=,解得BC=3米.
∵AC=5.4 m,∴AB=5.4-3=2.4(m).
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA.
又∵∠FCB=∠GAB,∴△BFC∽△BGA,
∴=,∴=,解得AG=1.2 m.
答:灯泡到地面的高度AG为1.2 m.
9.12
10.A 解析:(方法1)∵AB∶BC=3∶4,
∴设AB=3x,BC=4x,
∵∠ABC=90°,∴AC==5x.
∵BD⊥AC,∴∠ADB=∠ABC=90°.
∵∠BAD=∠CAB,∴△ABD∽△ACB,
∴=,∴=,∴AD=x.
∵AE平分∠BAC,
∴∠BAF=∠DAF,∴∠AEB=∠AFD,
∵∠AFD=∠BFE,∴∠BEF=∠BFE,∴BE=BF.
∵∠ABE=∠ADF=90°,∠BAE=∠DAF,
∴△ABE∽△ADF,∴=,
∴===.
(方法2)∵AB∶BC=3∶4,
∴设AB=3x,BC=4x.
∵∠ABC=90°,∴AC==5x.
∵BD⊥AC,∴∠ADB=∠ABC=90°.
∵∠BAD=∠CAB,∴△ABD∽△ACB,
∴=,∴=,∴AD=x.
如图,过F作FH⊥AB于H,
∵AE是∠BAC的平分线,
FD⊥AC,
∴FH=FD.
∵sin∠ABD==,
∴==.
故选A.
11.解:设BE=y m.由题意可知,
EF∥AB,GH∥AB,
∴△ABD∽△FED,△ABC∽△HGC,
∴=,=.
∵EF=HG=1.5 m,∴=,∴=,
解得y=26 m.∵=,∴=,解得AB=21 m.
答:该古建筑AB的高度为21 m.
12.(1)证明:∵四边形ABCD为矩形,
∴∠B=90°,AD∥BC,∴∠EAM=∠AMB.
∵EM⊥AM,∴∠AME=90°.
∵∠B=∠AME,∠AMB=∠EAM,
∴△ABM∽△EMA.
(2)解:∵AB=4,BM=3,∠B=90°,
∴AM===5.
∵△ABM∽△EMA,∴=,
即=,∴ME=.
13.(1)解:∵x2-7x+12=0,∴(x-3)(x-4)=0,
∴x1=3,x2=4.∵OA>OB,∴OA=4,OB=3.
(2)证明:∵S△AOE=,∴OA·OE=,
即×4OE=,∴OE=,
∴点E的坐标为(-,0)或(,0).
∵==,==,∴=.
∵四边形ABCD是平行四边形,∴AD∥BC.
∵∠AOE=90°,∴OE⊥OA,即BC⊥OA,∴OA⊥AD,
∴∠DAO=90°,∴∠AOE=∠DAO,∴△AOE∽△DAO.
14.解:(1)如图1所示,在OA延长线上取格点D,在OB延长线上取格点E,使OD=2OA,OE=2OB,连接DE,
则===2,
∵∠DOE=∠AOB,∴△ODE∽△OAB,
故△ODE即为所求作.
(2)如图2所示,在点A的下方取格点G,使AG=3,AG∥OB,连接BG交AO于点F,
则△AGF∽△OBF,
∵OB=2,∴==,
故点F即为所求作.
一、考点过关
考点1 比例性质
1.若=,则=( ).
A. B.- C.7 D.-7
考点2 平行线分线段成比例基本事实及其推论基本应用
2.如图,在△ABC中,点D在边AB上,过点D作DE∥BC,交AC于点E.若AD=2,BD=3,则的值是( ).
A. B. C. D.
考点3 黄金分割点
3.如图,若点D是线段AB的黄金分割点(AD>BD),AB=4,则AD的长是( ).
A.3 B.6-2 C.2-2 D.2-1
考点4 相似图形及其性质
4.如图,四边形ABCD和四边形EFGH相似,且顶点都在方格纸的格点上,它们的相似比是( ).
A.1∶2 B.1∶4 C.2∶1 D.4∶1
考点5 两三角形相似的判定及性质
5.如图是老师画出的△ABC,已标出三边的长度.下面四位同学画出的三角形与老师画出的△ABC不一定相似的是( ).
A B C D
6.(2024秋·深圳校级月考)如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C.
(1)求证:△ABD∽△ACB.
(2)若AB=6,AD=4,求线段CD的长.
考点6 位似图形及其坐标性质
7.如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,点A(-1.4,1.5)的对应点为A'(-0.2,-3),点C的坐标为(-1,0),若点B的对应点B'的横坐标为3,则点B的横坐标为 .
考点7 相似三角形的应用综合
8.如图,嘉嘉同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度DE=3.5 m,点F到地面的高度CF=1.5 m,灯泡到木板的水平距离AC=5.4 m,墙到木板的水平距离为CD=4 m.已知光在镜面反射中的入射角等于反射角,图中点A,B,C,D在同一水平面上.求灯泡到地面的高度AG.
二、核心考题
9.如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC的面积比是1∶4,若AB=6,则CD的长为 .
第9题图
10.如图,Rt△ABC中,∠ABC=90°,BD⊥AC,垂足为D,AE平分∠BAC,分别交BD,BC于点F,E.若AB∶BC=3∶4,则BF∶FD为( ).
第10题图
A.5∶3 B.5∶4 C.4∶3 D.2∶1
11.某数学兴趣小组决定利用所学知识测量一古建筑(如图1)的高度.如图2,古建筑的高度为AB,在地面BC上取E,G两点,分别竖立两根高为1.5 m的标杆EF和GH,两标杆间隔EG为26 m,并且古建筑AB、标杆EF和GH在同一竖直平面内.从标杆EF后退2 m到D处(即ED=2 m),从D处观察点A,A,F,D在同一直线上;从标杆GH后退4 m到C处(即CG=4 m),从C处观察点A,A,H,C三点也在同一直线上.已知点B,E,D,G,C在同一直线上,AB⊥BC,EF⊥BC,GH⊥BC,请你根据以上测量数据,帮助数学兴趣小组求出该古建筑AB的高度.
12.如图,在矩形ABCD中,M为BC上一点,EM⊥AM交AD的延长线于点E.
(1)求证:△ABM∽△EMA;
(2)若AB=4,BM=3,求ME的长.
三、提升考题
13.如图,在平面直角坐标系中, ABCD的边AD=6,若OA,OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
(1)求OA,OB的长;
(2)若x轴上有一个点E满足S△AOE=,求证:△AOE∽△DAO.
14.如图,在6×6的正方形网格中,每个小正方形的边长均相等,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)如图1,以点O为位似中心画△ODE,使得△ODE与△OAB位似,且相似比为2∶1,D,E为格点.
(2)如图2,在OA边上找一点F,使得=.
参考答案
1.B 2.A 3.C 4.C 5.C
6.解:(1)在△ABD和△ACB中,∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB.
(2)∵△ABD∽△ACB,∴=.
∵AB=6,AD=4,∴AC===9,
则CD=AC-AD=9-4=5.
7.-3 解析:过点A作AM⊥x轴于点M,过A'作A'N⊥x轴于点N(图略),则AM∥A'N,∴△ACM∽△A'CN,∴=.∵点A(-1.4,1.5)的对应点为A'(-0.2,-3),点C的坐标为(-1,0),∴===,∴△ABC和△A'B'C的相似比为1∶2.过点B作BE⊥x轴作于点E,过点B'作B'F⊥x轴于点F,则BE∥B'F,∴△BCE∽△B'CF,∴=,∵点C的坐标为(-1,0),点B'的横坐标为3,∴CF=4,∵△ABC和△A'B'C的相似比为1∶2,即=,∴=,解得EC=2,∴点B的横坐标为-3.
8.解:由题意可得FC∥DE,则
△BFC∽△BED,故=,
即=,解得BC=3米.
∵AC=5.4 m,∴AB=5.4-3=2.4(m).
∵光在镜面反射中的入射角等于反射角,
∴∠FBC=∠GBA.
又∵∠FCB=∠GAB,∴△BFC∽△BGA,
∴=,∴=,解得AG=1.2 m.
答:灯泡到地面的高度AG为1.2 m.
9.12
10.A 解析:(方法1)∵AB∶BC=3∶4,
∴设AB=3x,BC=4x,
∵∠ABC=90°,∴AC==5x.
∵BD⊥AC,∴∠ADB=∠ABC=90°.
∵∠BAD=∠CAB,∴△ABD∽△ACB,
∴=,∴=,∴AD=x.
∵AE平分∠BAC,
∴∠BAF=∠DAF,∴∠AEB=∠AFD,
∵∠AFD=∠BFE,∴∠BEF=∠BFE,∴BE=BF.
∵∠ABE=∠ADF=90°,∠BAE=∠DAF,
∴△ABE∽△ADF,∴=,
∴===.
(方法2)∵AB∶BC=3∶4,
∴设AB=3x,BC=4x.
∵∠ABC=90°,∴AC==5x.
∵BD⊥AC,∴∠ADB=∠ABC=90°.
∵∠BAD=∠CAB,∴△ABD∽△ACB,
∴=,∴=,∴AD=x.
如图,过F作FH⊥AB于H,
∵AE是∠BAC的平分线,
FD⊥AC,
∴FH=FD.
∵sin∠ABD==,
∴==.
故选A.
11.解:设BE=y m.由题意可知,
EF∥AB,GH∥AB,
∴△ABD∽△FED,△ABC∽△HGC,
∴=,=.
∵EF=HG=1.5 m,∴=,∴=,
解得y=26 m.∵=,∴=,解得AB=21 m.
答:该古建筑AB的高度为21 m.
12.(1)证明:∵四边形ABCD为矩形,
∴∠B=90°,AD∥BC,∴∠EAM=∠AMB.
∵EM⊥AM,∴∠AME=90°.
∵∠B=∠AME,∠AMB=∠EAM,
∴△ABM∽△EMA.
(2)解:∵AB=4,BM=3,∠B=90°,
∴AM===5.
∵△ABM∽△EMA,∴=,
即=,∴ME=.
13.(1)解:∵x2-7x+12=0,∴(x-3)(x-4)=0,
∴x1=3,x2=4.∵OA>OB,∴OA=4,OB=3.
(2)证明:∵S△AOE=,∴OA·OE=,
即×4OE=,∴OE=,
∴点E的坐标为(-,0)或(,0).
∵==,==,∴=.
∵四边形ABCD是平行四边形,∴AD∥BC.
∵∠AOE=90°,∴OE⊥OA,即BC⊥OA,∴OA⊥AD,
∴∠DAO=90°,∴∠AOE=∠DAO,∴△AOE∽△DAO.
14.解:(1)如图1所示,在OA延长线上取格点D,在OB延长线上取格点E,使OD=2OA,OE=2OB,连接DE,
则===2,
∵∠DOE=∠AOB,∴△ODE∽△OAB,
故△ODE即为所求作.
(2)如图2所示,在点A的下方取格点G,使AG=3,AG∥OB,连接BG交AO于点F,
则△AGF∽△OBF,
∵OB=2,∴==,
故点F即为所求作.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
