上海市杨浦区2024-2025学年高二下学期期中考试数学试题(图片版,含详解)
文档属性
| 名称 | 上海市杨浦区2024-2025学年高二下学期期中考试数学试题(图片版,含详解) | 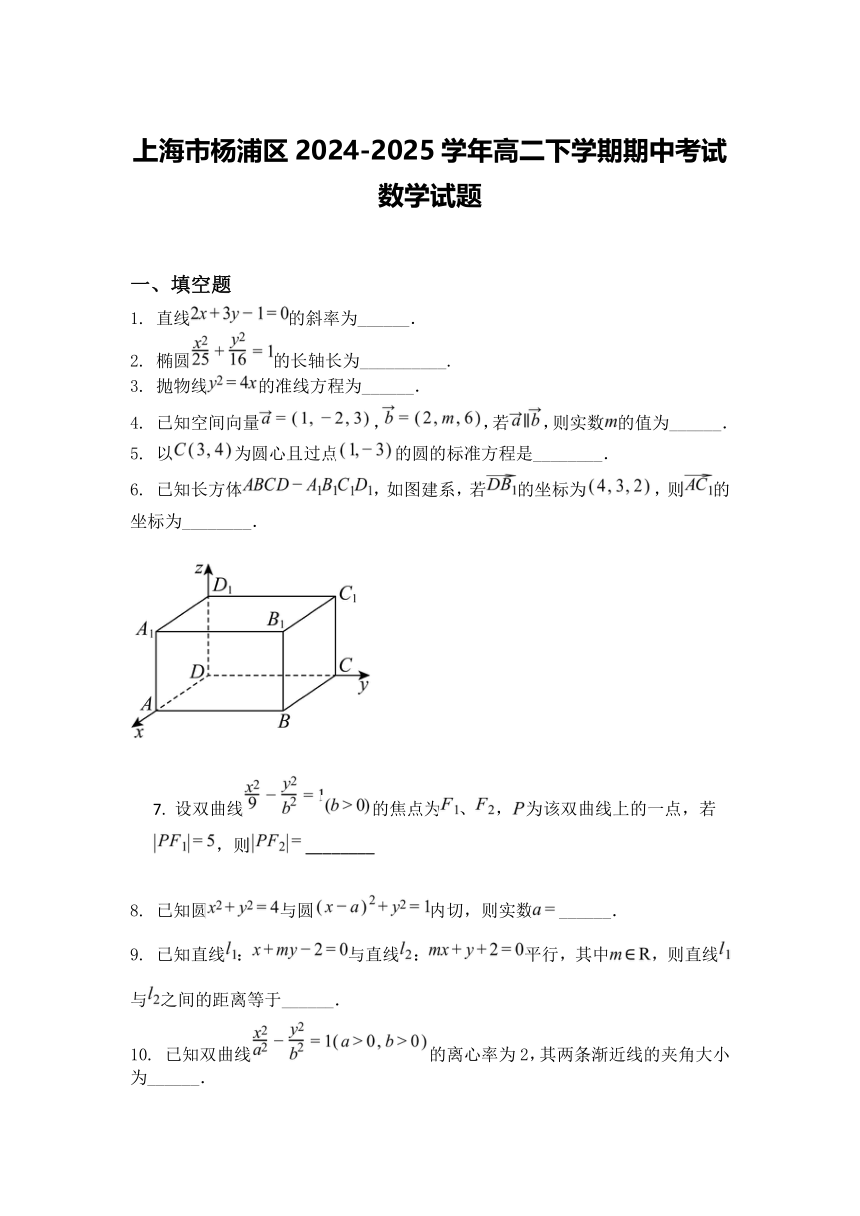 | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 15:52:26 | ||
图片预览




文档简介
上海市杨浦区 2024-2025 学年高二下学期期中考试
数学试题
一、填空题
1. 直线 的斜率为______.
2. 椭圆 的长轴长为__________.
3. 抛物线 的准线方程为______.
4. 已知空间向量 , ,若 ,则实数 的值为______.
5. 以 为圆心且过点 的圆的标准方程是________.
6. 已知长方体 ,如图建系,若 的坐标为 ,则 的
坐标为________.
7. 设双曲线 的焦点为 、 , 为该双曲线上的一点,若
,则 ________
8. 已知圆 与圆 内切,则实数 ______.
9. 已知直线 : 与直线 : 平行,其中 ,则直线
与 之间的距离等于______.
10. 已知双曲线 的离心率为 2,其两条渐近线的夹角大小
为______.
11. 斜率为 1的直线 过抛物线 的焦点 ,若 与圆
相切,则 等于______.
12. 已知抛物线 的焦点为 , , 是抛物线 上关于其对称轴对称的两点,
若 , 为坐标原点,则点 的横坐标为_____________.
二、单选题
13. 若直线 经过第一、二、四象限,则( )
A. 且 B. 且
C. 且 D. 且
14. 平面 的一个法向量为 ,点 在平面 内,则点
到平面 的距离为( )
A. B. C.1 D.
15. 已知双曲线 =1(a>0,b>0)的左、右焦点分别为 F1,F2,以 F1,F2
为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为( )
A. =1 B. =1
C. =1 D. =1
16. 过原点的直线 与双曲线 交于 两点,点 在第二象限,将下半平面沿
轴折起使之与上半平面成直二面角.则线段 的最短长度为
A. B. C. D.4
三、解答题
17. 已知 三个顶点坐标分别为 、 、 .
(1)求 的面积 S;
(2)求 边上的中线与 AC 边上的高的交点坐标.
18. 一辆卡车要通过跨度为 8米,拱高为 4米的抛物线形隧道,为了保证安全,
车顶上方与抛物线的铅垂距离至少 0.5 米.隧道有两条车道,车辆在其中一条车
道行驶,卡车宽为 2.2 米,车厢视为长方体,问卡车的限高为多少米?
19. 已知抛物线 的焦点为 F,点 在抛物线上,且 .
(1)求抛物线的方程;
(2)过焦点 F 的直线 l 交抛物线于 A、B 两点,若 ,求直线 l 的方程.
20. 如图所示,在直三棱柱 中, , , ,
D 是棱 的中点.
(1)求证: 平面 BCD;
(2)求二面角 的大小.
21. 已知椭圆 C: 过点 ,且右焦点为 .
(1)求椭圆 C 的方程;
(2)过点F的直线 l与椭圆C交于A、B两点,交y轴于点P.若 , ,
求证: 为定值.
上海市杨浦区 2024-2025 学年高二下学期期中考试数学试题
整体难度:适中
考试范围:平面解析几何、空间向量与立体几何、平面向量、竞赛知识点
试卷题型
题型 数量
填空题 12
单选题 4
解答题 5
试卷难度
难度 题数
容易 3
较易 10
适中 8
细目表分析
题号 难度系数 详细知识点
一、填空题
1 0.94 直线的斜截式方程及辨析;直线一般式方程与其他形式之间的互化
2 0.94 求椭圆的长轴、短轴
3 0.85 根据抛物线方程求焦点或准线
4 0.85 由空间向量共线求参数或值;空间向量平行的坐标表示
5 0.94 由圆心(或半径)求圆的方程
6 0.85 空间向量的坐标运算
7 0.85 双曲线定义的理解
8 0.85 由圆的位置关系确定参数或范围
9 0.65 已知直线平行求参数;求平行线间的距离
10 0.85 根据 a,b,c 齐次式关系求渐近线方程;求双曲线的离心率或离心率的取值范围
11 0.65 由直线与圆的位置关系求参数;根据抛物线方程求焦点或准线
12 0.65 根据抛物线方程求焦点或准线;利用向量垂直求参数
二、单选题
13 0.85 直线的斜截式方程及辨析;直线一般式方程与其他形式之间的互化
14 0.85 点到平面距离的向量求法
15 0.85 根据 a、b、c 求双曲线的标准方程;根据双曲线的渐近线求标准方程
16 0.65 空间中距离和角的计算
三、解答题
求直线交点坐标;求点到直线的距离;直线的点斜式方程及辨析;求平面两点间
17 0.65
的距离
18 0.65 抛物线的应用
求直线与抛物线相交所得弦的弦长;根据韦达定理求参数;根据抛物线上的点求
19 0.85
标准方程;直线与抛物线交点相关问题
20 0.65 证明线面垂直;面面角的向量求法;空间位置关系的向量证明
21 0.65 根据 a、b、c 求椭圆标准方程;椭圆中的定值问题
知识点分析
序号 知识点 对应题号
1 平面解析几何 1,2,3,5,7,8,9,10,11,12,13,15,17,18,19,21
2 空间向量与立体几何 4,6,14,20
3 平面向量 12
4 竞赛知识点 16
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
第 20 题:
第 21 题:
数学试题
一、填空题
1. 直线 的斜率为______.
2. 椭圆 的长轴长为__________.
3. 抛物线 的准线方程为______.
4. 已知空间向量 , ,若 ,则实数 的值为______.
5. 以 为圆心且过点 的圆的标准方程是________.
6. 已知长方体 ,如图建系,若 的坐标为 ,则 的
坐标为________.
7. 设双曲线 的焦点为 、 , 为该双曲线上的一点,若
,则 ________
8. 已知圆 与圆 内切,则实数 ______.
9. 已知直线 : 与直线 : 平行,其中 ,则直线
与 之间的距离等于______.
10. 已知双曲线 的离心率为 2,其两条渐近线的夹角大小
为______.
11. 斜率为 1的直线 过抛物线 的焦点 ,若 与圆
相切,则 等于______.
12. 已知抛物线 的焦点为 , , 是抛物线 上关于其对称轴对称的两点,
若 , 为坐标原点,则点 的横坐标为_____________.
二、单选题
13. 若直线 经过第一、二、四象限,则( )
A. 且 B. 且
C. 且 D. 且
14. 平面 的一个法向量为 ,点 在平面 内,则点
到平面 的距离为( )
A. B. C.1 D.
15. 已知双曲线 =1(a>0,b>0)的左、右焦点分别为 F1,F2,以 F1,F2
为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为( )
A. =1 B. =1
C. =1 D. =1
16. 过原点的直线 与双曲线 交于 两点,点 在第二象限,将下半平面沿
轴折起使之与上半平面成直二面角.则线段 的最短长度为
A. B. C. D.4
三、解答题
17. 已知 三个顶点坐标分别为 、 、 .
(1)求 的面积 S;
(2)求 边上的中线与 AC 边上的高的交点坐标.
18. 一辆卡车要通过跨度为 8米,拱高为 4米的抛物线形隧道,为了保证安全,
车顶上方与抛物线的铅垂距离至少 0.5 米.隧道有两条车道,车辆在其中一条车
道行驶,卡车宽为 2.2 米,车厢视为长方体,问卡车的限高为多少米?
19. 已知抛物线 的焦点为 F,点 在抛物线上,且 .
(1)求抛物线的方程;
(2)过焦点 F 的直线 l 交抛物线于 A、B 两点,若 ,求直线 l 的方程.
20. 如图所示,在直三棱柱 中, , , ,
D 是棱 的中点.
(1)求证: 平面 BCD;
(2)求二面角 的大小.
21. 已知椭圆 C: 过点 ,且右焦点为 .
(1)求椭圆 C 的方程;
(2)过点F的直线 l与椭圆C交于A、B两点,交y轴于点P.若 , ,
求证: 为定值.
上海市杨浦区 2024-2025 学年高二下学期期中考试数学试题
整体难度:适中
考试范围:平面解析几何、空间向量与立体几何、平面向量、竞赛知识点
试卷题型
题型 数量
填空题 12
单选题 4
解答题 5
试卷难度
难度 题数
容易 3
较易 10
适中 8
细目表分析
题号 难度系数 详细知识点
一、填空题
1 0.94 直线的斜截式方程及辨析;直线一般式方程与其他形式之间的互化
2 0.94 求椭圆的长轴、短轴
3 0.85 根据抛物线方程求焦点或准线
4 0.85 由空间向量共线求参数或值;空间向量平行的坐标表示
5 0.94 由圆心(或半径)求圆的方程
6 0.85 空间向量的坐标运算
7 0.85 双曲线定义的理解
8 0.85 由圆的位置关系确定参数或范围
9 0.65 已知直线平行求参数;求平行线间的距离
10 0.85 根据 a,b,c 齐次式关系求渐近线方程;求双曲线的离心率或离心率的取值范围
11 0.65 由直线与圆的位置关系求参数;根据抛物线方程求焦点或准线
12 0.65 根据抛物线方程求焦点或准线;利用向量垂直求参数
二、单选题
13 0.85 直线的斜截式方程及辨析;直线一般式方程与其他形式之间的互化
14 0.85 点到平面距离的向量求法
15 0.85 根据 a、b、c 求双曲线的标准方程;根据双曲线的渐近线求标准方程
16 0.65 空间中距离和角的计算
三、解答题
求直线交点坐标;求点到直线的距离;直线的点斜式方程及辨析;求平面两点间
17 0.65
的距离
18 0.65 抛物线的应用
求直线与抛物线相交所得弦的弦长;根据韦达定理求参数;根据抛物线上的点求
19 0.85
标准方程;直线与抛物线交点相关问题
20 0.65 证明线面垂直;面面角的向量求法;空间位置关系的向量证明
21 0.65 根据 a、b、c 求椭圆标准方程;椭圆中的定值问题
知识点分析
序号 知识点 对应题号
1 平面解析几何 1,2,3,5,7,8,9,10,11,12,13,15,17,18,19,21
2 空间向量与立体几何 4,6,14,20
3 平面向量 12
4 竞赛知识点 16
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
第 20 题:
第 21 题:
同课章节目录
