第一章 反比例函数 单元练习卷(含部分解析) 2025-2026学年湘教版九年级数学上册-普通用卷
文档属性
| 名称 | 第一章 反比例函数 单元练习卷(含部分解析) 2025-2026学年湘教版九年级数学上册-普通用卷 |  | |
| 格式 | docx | ||
| 文件大小 | 109.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 23:51:17 | ||
图片预览



文档简介
第一章 反比例函数 单元练习卷 2025-2026学年湘教版九年级数学上册
一、选择题:本题共8小题,每小题3分,共24分。
1.当时,函数的图象在( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
2.下列函数是反比例函数的是( )
A. B. C. D.
3.已知反比例函数的图象经过点,则该函数的图象位于( )
A. 第一、三象限 B. 第二、三象限 C. 第二、四象限 D. 第三、四象限
4.已知双曲线过点,,,则下列结论中,正确的是( )
A. B. C. D.
5.将反比例函数的图像向下平移个单位长度后,新图像与轴的交点坐标是( )
A. B. C. D.
6.已知点,是反比例函数的图象上的两点,若,则下列结论正确的是( )
A. B. C. D.
7.体育课上,甲、乙、丙、丁四位同学进行跑步训练.如图,用四个点分别描述这四位同学的跑步时间与平均跑步速度之间的关系,其中描述甲、丙两位同学的与之间关系的点恰好在同一个反比例函数的图像上,则在这次训练中跑的路程最多的是( )
A. 甲 B. 乙 C. 丙 D. 丁
8.某闭合电路中,电源电压为定值,电流与电阻成反比例,如下图所表示的是该电路中电流与电阻之间的函数关系的图象,则用电阻表示电流的函数解析式为( )
A. B. C. D.
二、填空题:本题共8小题,每小题3分,共24分。
9.已知函数是反比例函数,则 .
10.若双曲线在每一个象限内,随的增大而增大,则的取值范围是 .
11.把一个长、宽、高分别为,,的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积与高之间的函数表达式为 .
12.点,都在反比例函数的图像上,则 填“”或“”或“”
13.在平面直角坐标系中,若函数的图象经过点和,则的值是 .
14.若反比例函数的图像位于第一、三象限,正比例函数的图像过第二、四象限,则的整数值是 .
15.如图,点是第二象限内的一点,且在反比例函数的图象上,过点作轴于点,若的面积为,则的值为______.
16.如图,平行四边形的边在轴上,顶点在反比例函数的图象上,与轴相交于点,且为的中点,若平行四边形的面积为,则 .
三、解答题:本题共6小题,共52分。
17.本小题分
某市计划修建一条长的轻轨铁路.
原计划每月修建,个月可修建完.求与之间的函数表达式;
为使工程能提前个月完成,需要将原定的工作效率提高原计划完成这项工程用多少个月?
18.本小题分
如果点,都在反比例函数的图象上,并且,试比较,的大小.
19.本小题分
已知与成反比例,并且当时,.
写出与之间的函数表达式;
当时,求的值;
当时,求的值.
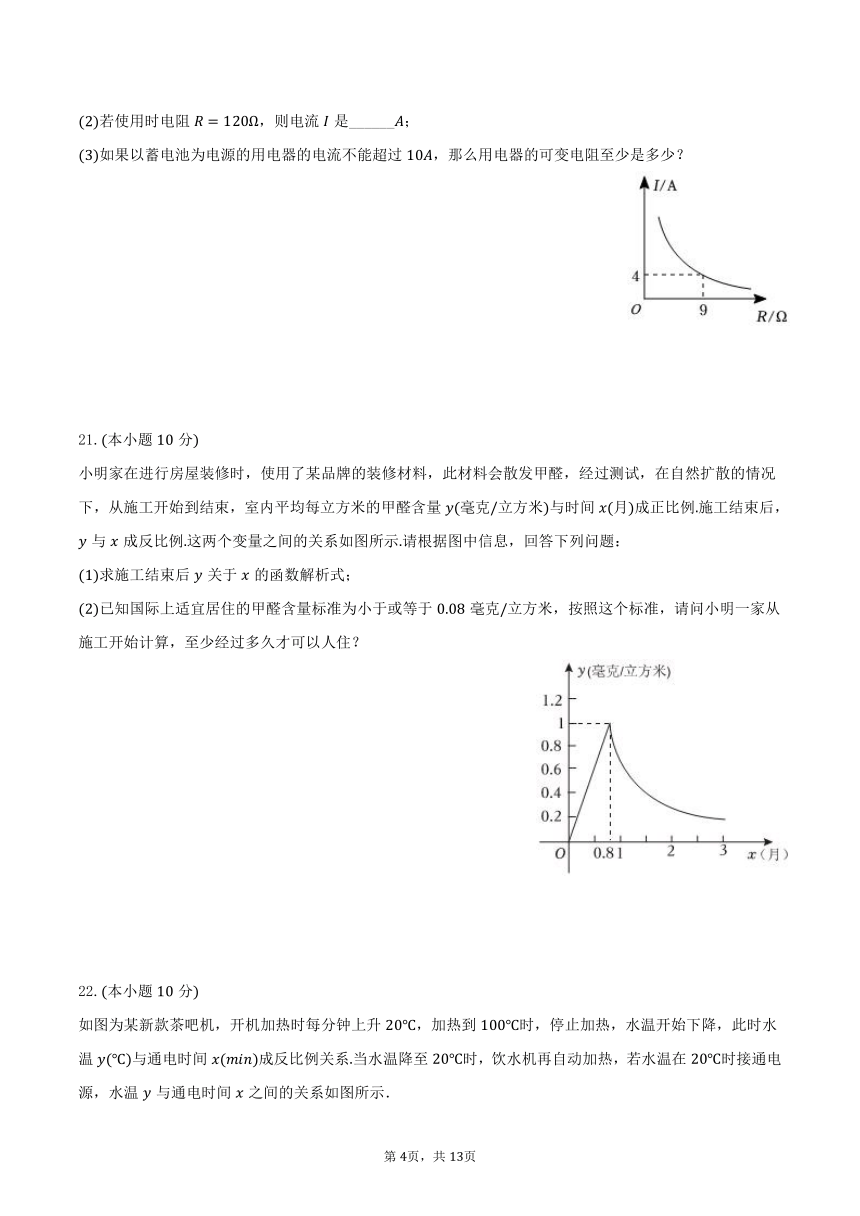
20.本小题分
已知蓄电池的电压为定值,使用蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示.
这个反比例函数的解析式是______;
若使用时电阻,则电流是______;
如果以蓄电池为电源的用电器的电流不能超过,那么用电器的可变电阻至少是多少?
21.本小题分
小明家在进行房屋装修时,使用了某品牌的装修材料,此材料会散发甲醛,经过测试,在自然扩散的情况下,从施工开始到结束,室内平均每立方米的甲醛含量毫克立方米与时间月成正比例施工结束后,与成反比例这两个变量之间的关系如图所示请根据图中信息,回答下列问题:
求施工结束后关于的函数解析式;
已知国际上适宜居住的甲醛含量标准为小于或等于毫克立方米,按照这个标准,请问小明一家从施工开始计算,至少经过多久才可以人住?
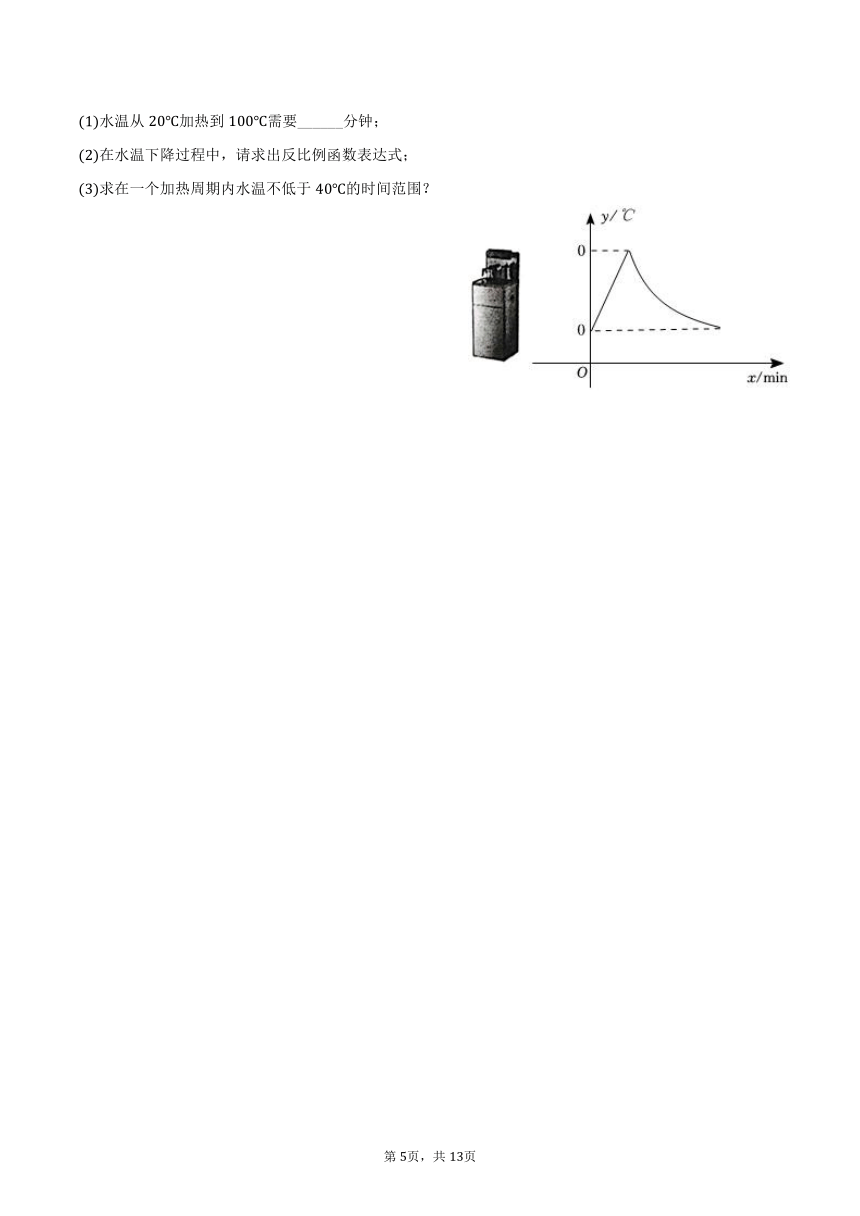
22.本小题分
如图为某新款茶吧机,开机加热时每分钟上升,加热到时,停止加热,水温开始下降,此时水温与通电时间成反比例关系当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示.
水温从加热到需要______分钟;
在水温下降过程中,请求出反比例函数表达式;
求在一个加热周期内水温不低于的时间范围?
答案和解析
1.【答案】
【解析】解:函数中,,
函数图象在第二、四象限.
又,
函数的图象在第二象限.
故选:.
利用反比例函数的性质,时,函数图象位于第二、四象限,再根据即可解答.
本题考查反比例函数的性质:
当时,图象分别位于第一、三象限;当时,图象分别位于第二、四象限.
当时,在同一象限内,随的增大而减小;当时,在同一象限内,随的增大而增大.
2.【答案】
【解析】【分析】
本题考查了反比例函数,熟记反比例函数的定义是解题关键.
根据反比例函数的定义,可得答案.
【解答】
解:、符合正比例函数的定义,故A错误;
B、不符合反比例函数的定义,故B错误;
C、不符合反比例函数的定义,故C错误;
D、符合反比例函数的定义,故D正确;
故选:.
3.【答案】
【解析】解:反比例函数的图象经过点,
,
该函数的图象位于一、三象限;
故选:.
根据反比例函数图象上的点的横纵坐标的积是定值,即,求出的值,再根据,判断所经过象限.
本题主要考查了反比例函数图象上点的坐标特征、反比例函数的性质,熟练掌握反比例函数图象上的点的横纵坐标的积是定值是解题关键.
4.【答案】
【解析】,反比例函数的图像在第二、四象限,在每个象限内,随的增大而增大.反比例函数的图像过点,,,点,在第四象限,点在第二象限.,故选A.
5.【答案】
【解析】略
6.【答案】
【解析】解:,是反比例函数的图象上的两点,
,,
,
.
故选:.
7.【答案】
【解析】略
8.【答案】
【解析】【分析】
此题主要考查了待定系数法求反比例函数解析式,关键是掌握凡是函数图象经过的点必能满足解析式.
根据函数图象可用电阻表示电流的函数解析式为,再把代入可得的值,进而可得函数解析式.
【解答】
解:设用电阻表示电流的函数解析式为,
过,
,
,
故选A.
9.【答案】
【解析】【分析】
本题考查反比例函数的定义,熟记反比例函数解析式的一般式是解决此类问题的关键.根据反比例函数的定义列出方程,解出的值即可.
【解答】
解:若函数是反比例函数,
则
解得,
故答案为:
10.【答案】
【解析】解:双曲线在每一个象限内,随的增大而增大,
,
,
故答案为:.
根据反比例函数的增减性可得,进一步可得的取值范围.
本题考查了反比例函数的性质,熟练掌握反比例函数的性质与系数的关系是解题的关键.
11.【答案】
【解析】略
12.【答案】
【解析】本题考查的是比较反比例函数值或自变量的大小,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解题的关键.先分别将点的坐标代入解析式求出,的值,再比较大小即可求解.
【详解】解:点,都在反比例函数的图象上,
故将,代入,得,,
,
.
故答案为:.
13.【答案】
【解析】本题考查了反比例函数图像点的坐标特征,已知自变量求函数值,熟练掌握知识点是解题的关键.
将点和代入,求得和,再相加即可.
【详解】解:函数的图象经过点和,
有,
,
故答案为:.
14.【答案】
【解析】根据题意,得且,解得因为为整数,所以.
15.【答案】
【解析】解:由题意得,
解答,
又,
,
故答案为:.
根据反比例函数的几何意义,可得,进而求出的值,检验得出答案.
本题考查反比例函数的几何意义,理解的几何意义是正确解答的前提.
16.【答案】
【解析】【分析】
本题考查了反比例函数系数的几何意义,根据题意得的面积为平行四边形的面积的是关键.
由为的中点,平行四边形的面积为,可得的面积为平行四边形的面积的,再根据反比例函数系数的几何意义即可求出答案.
【解答】
解:为的中点,平行四边形的面积为,
的面积为,
,
,
.
故答案为:.
17.【答案】【小题】
解:根据题意,得,.
【小题】
根据题意,得,解得。经检验,是所列方程的解,且符合题意。将代入,得.
答:原计划完成这项工程用个月.
【解析】 见答案
见答案
18.【答案】解:,反比例函数在每一个象限内都随的增大而减小.
,.
【解析】见答案
19.【答案】【小题】
解:设与之间的函数表达式为。将,代入上式,得,解得,所以与之间的函数表达式为.
【小题】
当时,.
【小题】
当时,,解得.
【解析】 见答案
见答案
见答案
20.【答案】;
;
.
【解析】解:设反比例函数式.
把代入反比例函数式,
.
.
故答案为:.
当,.
故答案为:;
当时,则,
,
用电器的可变电阻至少是.
先由电流是电阻的反比例函数,可设,结合点在函数图象上,利用待定系数法即可求出这个反比例函数的解析式;
中,令,求出对应的的值即可;
将代入所求的函数解析式,即可确定电阻的取值范围.
本题考查了反比例函数的应用,解题的关键是正确地从中整理出函数模型,并利用函数的知识解决实际问题.
21.【答案】施工结束后关于的函数解析式为:;
小明一家从施工开始计算,至少经过个月才可以入住.
【解析】解:当时,设,
经过点,
,
施工结束后关于的函数解析式为:.
当时,.
答:小明一家从施工开始计算,至少经过个月才可以入住.
施工结束后与成反比例函数,设出反比例函数解析式,把代入即可求得相应的函数解析式;
当,得到相应的的值即为可以入住的时间.
本题综合考查反比例函数的应用.用待定系数法求得不同取值范围内的函数解析式是解决本题的关键.
22.【答案】;
设水温下降过程中,与的函数关系式为,
由题意得,点在反比例函数的图象上,
,
解得:,
水温下降过程中,与的函数关系式是;
在加热过程中,水温为时,,
解得:,
在降温过程中,水温为时,,
解得:,
,
一个加热周期内水温不低于的时间为.
【解析】解:开机加热时每分钟上升,
水温从加热到,所需时间为,
故答案为:;
设水温下降过程中,与的函数关系式为,
由题意得,点在反比例函数的图象上,
,
解得:,
水温下降过程中,与的函数关系式是;
在加热过程中,水温为时,,
解得:,
在降温过程中,水温为时,,
解得:,
,
一个加热周期内水温不低于的时间为.
根据水温升高的速度,即可求出水温从加热到所需的时间;
设水温下降过程中,与的函数关系式为,根据待定系数法即可求解;
分别求出在加热过程和降温过程中水温为摄氏度时的时间,再相减即可判断.
本题主要考查反比例函数和一次函数的应用、用待定系数法求反比例函数解析数,解题关键在于读懂图象,灵活运用所学知识解决问题.
第1页,共13页
一、选择题:本题共8小题,每小题3分,共24分。
1.当时,函数的图象在( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
2.下列函数是反比例函数的是( )
A. B. C. D.
3.已知反比例函数的图象经过点,则该函数的图象位于( )
A. 第一、三象限 B. 第二、三象限 C. 第二、四象限 D. 第三、四象限
4.已知双曲线过点,,,则下列结论中,正确的是( )
A. B. C. D.
5.将反比例函数的图像向下平移个单位长度后,新图像与轴的交点坐标是( )
A. B. C. D.
6.已知点,是反比例函数的图象上的两点,若,则下列结论正确的是( )
A. B. C. D.
7.体育课上,甲、乙、丙、丁四位同学进行跑步训练.如图,用四个点分别描述这四位同学的跑步时间与平均跑步速度之间的关系,其中描述甲、丙两位同学的与之间关系的点恰好在同一个反比例函数的图像上,则在这次训练中跑的路程最多的是( )
A. 甲 B. 乙 C. 丙 D. 丁
8.某闭合电路中,电源电压为定值,电流与电阻成反比例,如下图所表示的是该电路中电流与电阻之间的函数关系的图象,则用电阻表示电流的函数解析式为( )
A. B. C. D.
二、填空题:本题共8小题,每小题3分,共24分。
9.已知函数是反比例函数,则 .
10.若双曲线在每一个象限内,随的增大而增大,则的取值范围是 .
11.把一个长、宽、高分别为,,的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积与高之间的函数表达式为 .
12.点,都在反比例函数的图像上,则 填“”或“”或“”
13.在平面直角坐标系中,若函数的图象经过点和,则的值是 .
14.若反比例函数的图像位于第一、三象限,正比例函数的图像过第二、四象限,则的整数值是 .
15.如图,点是第二象限内的一点,且在反比例函数的图象上,过点作轴于点,若的面积为,则的值为______.
16.如图,平行四边形的边在轴上,顶点在反比例函数的图象上,与轴相交于点,且为的中点,若平行四边形的面积为,则 .
三、解答题:本题共6小题,共52分。
17.本小题分
某市计划修建一条长的轻轨铁路.
原计划每月修建,个月可修建完.求与之间的函数表达式;
为使工程能提前个月完成,需要将原定的工作效率提高原计划完成这项工程用多少个月?
18.本小题分
如果点,都在反比例函数的图象上,并且,试比较,的大小.
19.本小题分
已知与成反比例,并且当时,.
写出与之间的函数表达式;
当时,求的值;
当时,求的值.
20.本小题分
已知蓄电池的电压为定值,使用蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示.
这个反比例函数的解析式是______;
若使用时电阻,则电流是______;
如果以蓄电池为电源的用电器的电流不能超过,那么用电器的可变电阻至少是多少?
21.本小题分
小明家在进行房屋装修时,使用了某品牌的装修材料,此材料会散发甲醛,经过测试,在自然扩散的情况下,从施工开始到结束,室内平均每立方米的甲醛含量毫克立方米与时间月成正比例施工结束后,与成反比例这两个变量之间的关系如图所示请根据图中信息,回答下列问题:
求施工结束后关于的函数解析式;
已知国际上适宜居住的甲醛含量标准为小于或等于毫克立方米,按照这个标准,请问小明一家从施工开始计算,至少经过多久才可以人住?
22.本小题分
如图为某新款茶吧机,开机加热时每分钟上升,加热到时,停止加热,水温开始下降,此时水温与通电时间成反比例关系当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示.
水温从加热到需要______分钟;
在水温下降过程中,请求出反比例函数表达式;
求在一个加热周期内水温不低于的时间范围?
答案和解析
1.【答案】
【解析】解:函数中,,
函数图象在第二、四象限.
又,
函数的图象在第二象限.
故选:.
利用反比例函数的性质,时,函数图象位于第二、四象限,再根据即可解答.
本题考查反比例函数的性质:
当时,图象分别位于第一、三象限;当时,图象分别位于第二、四象限.
当时,在同一象限内,随的增大而减小;当时,在同一象限内,随的增大而增大.
2.【答案】
【解析】【分析】
本题考查了反比例函数,熟记反比例函数的定义是解题关键.
根据反比例函数的定义,可得答案.
【解答】
解:、符合正比例函数的定义,故A错误;
B、不符合反比例函数的定义,故B错误;
C、不符合反比例函数的定义,故C错误;
D、符合反比例函数的定义,故D正确;
故选:.
3.【答案】
【解析】解:反比例函数的图象经过点,
,
该函数的图象位于一、三象限;
故选:.
根据反比例函数图象上的点的横纵坐标的积是定值,即,求出的值,再根据,判断所经过象限.
本题主要考查了反比例函数图象上点的坐标特征、反比例函数的性质,熟练掌握反比例函数图象上的点的横纵坐标的积是定值是解题关键.
4.【答案】
【解析】,反比例函数的图像在第二、四象限,在每个象限内,随的增大而增大.反比例函数的图像过点,,,点,在第四象限,点在第二象限.,故选A.
5.【答案】
【解析】略
6.【答案】
【解析】解:,是反比例函数的图象上的两点,
,,
,
.
故选:.
7.【答案】
【解析】略
8.【答案】
【解析】【分析】
此题主要考查了待定系数法求反比例函数解析式,关键是掌握凡是函数图象经过的点必能满足解析式.
根据函数图象可用电阻表示电流的函数解析式为,再把代入可得的值,进而可得函数解析式.
【解答】
解:设用电阻表示电流的函数解析式为,
过,
,
,
故选A.
9.【答案】
【解析】【分析】
本题考查反比例函数的定义,熟记反比例函数解析式的一般式是解决此类问题的关键.根据反比例函数的定义列出方程,解出的值即可.
【解答】
解:若函数是反比例函数,
则
解得,
故答案为:
10.【答案】
【解析】解:双曲线在每一个象限内,随的增大而增大,
,
,
故答案为:.
根据反比例函数的增减性可得,进一步可得的取值范围.
本题考查了反比例函数的性质,熟练掌握反比例函数的性质与系数的关系是解题的关键.
11.【答案】
【解析】略
12.【答案】
【解析】本题考查的是比较反比例函数值或自变量的大小,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解题的关键.先分别将点的坐标代入解析式求出,的值,再比较大小即可求解.
【详解】解:点,都在反比例函数的图象上,
故将,代入,得,,
,
.
故答案为:.
13.【答案】
【解析】本题考查了反比例函数图像点的坐标特征,已知自变量求函数值,熟练掌握知识点是解题的关键.
将点和代入,求得和,再相加即可.
【详解】解:函数的图象经过点和,
有,
,
故答案为:.
14.【答案】
【解析】根据题意,得且,解得因为为整数,所以.
15.【答案】
【解析】解:由题意得,
解答,
又,
,
故答案为:.
根据反比例函数的几何意义,可得,进而求出的值,检验得出答案.
本题考查反比例函数的几何意义,理解的几何意义是正确解答的前提.
16.【答案】
【解析】【分析】
本题考查了反比例函数系数的几何意义,根据题意得的面积为平行四边形的面积的是关键.
由为的中点,平行四边形的面积为,可得的面积为平行四边形的面积的,再根据反比例函数系数的几何意义即可求出答案.
【解答】
解:为的中点,平行四边形的面积为,
的面积为,
,
,
.
故答案为:.
17.【答案】【小题】
解:根据题意,得,.
【小题】
根据题意,得,解得。经检验,是所列方程的解,且符合题意。将代入,得.
答:原计划完成这项工程用个月.
【解析】 见答案
见答案
18.【答案】解:,反比例函数在每一个象限内都随的增大而减小.
,.
【解析】见答案
19.【答案】【小题】
解:设与之间的函数表达式为。将,代入上式,得,解得,所以与之间的函数表达式为.
【小题】
当时,.
【小题】
当时,,解得.
【解析】 见答案
见答案
见答案
20.【答案】;
;
.
【解析】解:设反比例函数式.
把代入反比例函数式,
.
.
故答案为:.
当,.
故答案为:;
当时,则,
,
用电器的可变电阻至少是.
先由电流是电阻的反比例函数,可设,结合点在函数图象上,利用待定系数法即可求出这个反比例函数的解析式;
中,令,求出对应的的值即可;
将代入所求的函数解析式,即可确定电阻的取值范围.
本题考查了反比例函数的应用,解题的关键是正确地从中整理出函数模型,并利用函数的知识解决实际问题.
21.【答案】施工结束后关于的函数解析式为:;
小明一家从施工开始计算,至少经过个月才可以入住.
【解析】解:当时,设,
经过点,
,
施工结束后关于的函数解析式为:.
当时,.
答:小明一家从施工开始计算,至少经过个月才可以入住.
施工结束后与成反比例函数,设出反比例函数解析式,把代入即可求得相应的函数解析式;
当,得到相应的的值即为可以入住的时间.
本题综合考查反比例函数的应用.用待定系数法求得不同取值范围内的函数解析式是解决本题的关键.
22.【答案】;
设水温下降过程中,与的函数关系式为,
由题意得,点在反比例函数的图象上,
,
解得:,
水温下降过程中,与的函数关系式是;
在加热过程中,水温为时,,
解得:,
在降温过程中,水温为时,,
解得:,
,
一个加热周期内水温不低于的时间为.
【解析】解:开机加热时每分钟上升,
水温从加热到,所需时间为,
故答案为:;
设水温下降过程中,与的函数关系式为,
由题意得,点在反比例函数的图象上,
,
解得:,
水温下降过程中,与的函数关系式是;
在加热过程中,水温为时,,
解得:,
在降温过程中,水温为时,,
解得:,
,
一个加热周期内水温不低于的时间为.
根据水温升高的速度,即可求出水温从加热到所需的时间;
设水温下降过程中,与的函数关系式为,根据待定系数法即可求解;
分别求出在加热过程和降温过程中水温为摄氏度时的时间,再相减即可判断.
本题主要考查反比例函数和一次函数的应用、用待定系数法求反比例函数解析数,解题关键在于读懂图象,灵活运用所学知识解决问题.
第1页,共13页
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
