广东省清远市清新区第三中学2024-2025学年高二下学期期中考试数学试题(图片版,含详解)
文档属性
| 名称 | 广东省清远市清新区第三中学2024-2025学年高二下学期期中考试数学试题(图片版,含详解) |  | |
| 格式 | |||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-01 16:00:20 | ||
图片预览



文档简介
广东省清远市清新区第三中学 2024-2025 学年高二
下学期期中考试数学试题
一、单选题
1. 下列叙述中,是离散型随机变量的是( )
A.某电子元件的寿命
B.高速公路上某收费站在一小时内经过的车辆数
C.某人早晨在车站等出租车的时间
D.测量某零件的长度产生的测量误差
2. 下列求导运算中,正确的一项是( )
A. B.
C. D.
3. 若函数 ,则 ( )
A.3 B.6 C. D.
4. 曲线 在点 处的切线方程为( )
A. B.
C. D.
5. 已知函数 ,则 的极大值为( )
A. B. C. D.
6. 已知在 A,B,C 三个地区暴发了流感,这三个地区分别有 6%,5%,4%的人
患了流感.假设这三个地区人口数量的比为 3:2:1,现从这三个地区中任意选
取一个人,则这个人患流感的概率为( )
A. B. C. D.
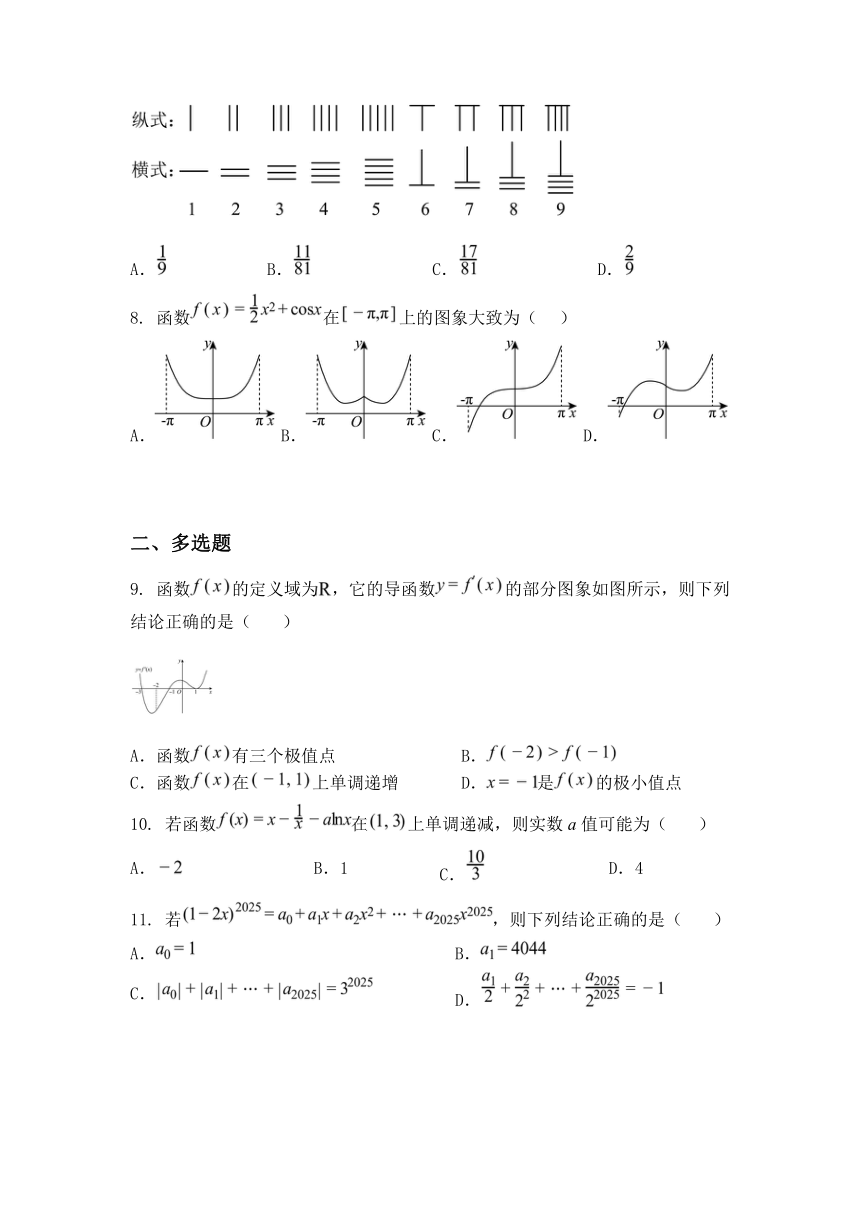
7. 根据历史记载,早在春秋战国时期,我国劳动人民就普遍使用算筹进行计数.
算筹计数法就是用一根根同样长短和粗细的小棍子(用竹子、木头、兽骨、象牙、
金属等材料制成)以不同的排列方式来表示数字,如图所示.如果用算筹随机摆
出一个不含数字 0的两位数,个位用纵式,十位用横式,则个位和十位上的算筹
一样多的概率为( )
A. B. C. D.
8. 函数 在 上的图象大致为( )
A. B. C. D.
二、多选题
9. 函数 的定义域为 ,它的导函数 的部分图象如图所示,则下列
结论正确的是( )
A.函数 有三个极值点 B.
C.函数 在 上单调递增 D. 是 的极小值点
10. 若函数 在 上单调递减,则实数 a 值可能为( )
A. B.1 C. D.4
11. 若 ,则下列结论正确的是( )
A. B.
C. D.
三、填空题
12. 已知随机变量 的分布列如下表,若 ,则 a=________, ______.
0 1 2
P a b
13. 某数学兴趣小组的 5名学生负责讲述“宋元数学四大家”——秦九韶、李冶、
杨辉和朱世杰的故事,每名学生只讲一个数学家的故事,每个数学家的故事都有
学生讲述,则不同的分配方案有______种.
14. 的展开式中,常数项为__________.
四、解答题
15. 已知口袋中有 2个白球和 4个红球,现从中随机抽取两次,每次抽取 1个.
(1)若采取放回的方法连续抽取两次,求两次都取得白球的概率;
(2)若采取不放回的方法连续抽取两次,求两次至少有一次取得白球的概率;
(3)若采取不放回的方法连续抽取两次,求在第一次取出红球的条件下,第二次
取出的是红球的概率.
16. 已知函数 .
(1)求函数 的单调区间;
(2)求函数 在区间 中的最大值.
17. 已知 的二项展开式有 7项.
(1)求 ,并求出所有二项式系数之和;
(2)求展开式中含 项的系数;
(3)求展开式中的有理项.
18. 当前,以 ChatGPT 为代表的 AIGC(利用 AI 技术自动生成内容的生产方式)
领域一系列创新技术有了革命性突破,全球各大科技企业都在积极拥抱 AIGC,
我国的 BAT(百度、阿里、腾讯 3个企业的简称)、字节跳动、万兴科技、蓝色
光标、华为等领头企业已纷纷加码布局 AIGC 赛道,某传媒公司准备发布《2023
年中国 AIGC 发展研究报告》,先期准备从上面 7个科技企业中随机选取 3个进行
采访.
(1)求选取的 3个科技企业中,BAT 中至多有 1个的概率;
(2)记选取的 3个科技企业中 BAT 中的个数为 ,求 的分布列与期望.
19. 已知函数 .
(1)若曲线 在点 处的切线与 轴平行,求实数 的值;
(2)若函数 在 内存在极值,求实数 的取值范围;
(3)若对任意的实数 , 恒成立,求实数 的取值范围.
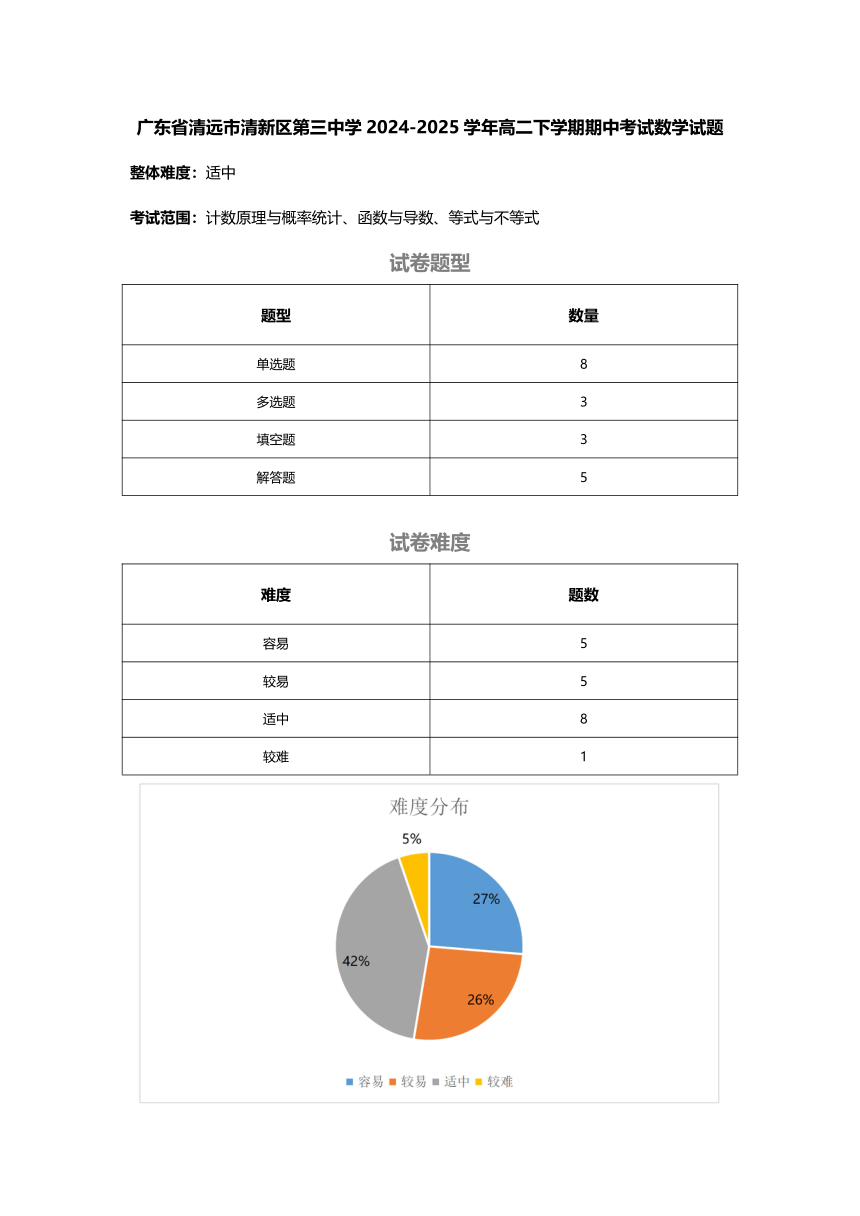
广东省清远市清新区第三中学 2024-2025 学年高二下学期期中考试数学试题
整体难度:适中
考试范围:计数原理与概率统计、函数与导数、等式与不等式
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 5
较易 5
适中 8
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 离散型随机变量与连续型随机变量的区分;判断随机试验中的随机变量
2 0.94 基本初等函数的导数公式
3 0.94 求某点处的导数值
4 0.94 求在曲线上一点处的切线方程(斜率)
5 0.94 求已知函数的极值
6 0.65 计算条件概率;利用全概率公式求概率
7 0.85 计算古典概型问题的概率;分类加法计数原理;分步乘法计数原理及简单应用
函数奇偶性的定义与判断;用导数判断或证明已知函数的单调性;函数图像的识
8 0.65
别
二、多选题
9 0.85 函数与导函数图象之间的关系;函数(导函数)图像与极值点的关系
10 0.65 由函数在区间上的单调性求参数;对勾函数求最值
11 0.65 求指定项的系数;二项展开式各项的系数和
三、填空题
12 0.85 离散型随机变量的方差与标准差;由离散型随机变量的均值求参数
13 0.65 全排列问题;分组分配问题;分步乘法计数原理及简单应用;排列组合综合
14 0.65 三项展开式的系数问题
四、解答题
15 0.65 计算条件概率;独立事件的乘法公式;利用对立事件的概率公式求概率
16 0.85 利用导数求函数的单调区间(不含参);由导数求函数的最值(不含参)
17 0.65 求指定项的系数;求有理项或其系数;二项式的系数和
写出简单离散型随机变量分布列;求离散型随机变量的均值;实际问题中的组合
18 0.85
计数问题;计算古典概型问题的概率
根据极值求参数;利用导数研究不等式恒成立问题;已知切线(斜率)求参数;
19 0.4
利用导数研究函数的零点
知识点分析
序号 知识点 对应题号
1 计数原理与概率统计 1,6,7,11,12,13,14,15,17,18
2 函数与导数 2,3,4,5,8,9,10,16,19
3 等式与不等式 10
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
下学期期中考试数学试题
一、单选题
1. 下列叙述中,是离散型随机变量的是( )
A.某电子元件的寿命
B.高速公路上某收费站在一小时内经过的车辆数
C.某人早晨在车站等出租车的时间
D.测量某零件的长度产生的测量误差
2. 下列求导运算中,正确的一项是( )
A. B.
C. D.
3. 若函数 ,则 ( )
A.3 B.6 C. D.
4. 曲线 在点 处的切线方程为( )
A. B.
C. D.
5. 已知函数 ,则 的极大值为( )
A. B. C. D.
6. 已知在 A,B,C 三个地区暴发了流感,这三个地区分别有 6%,5%,4%的人
患了流感.假设这三个地区人口数量的比为 3:2:1,现从这三个地区中任意选
取一个人,则这个人患流感的概率为( )
A. B. C. D.
7. 根据历史记载,早在春秋战国时期,我国劳动人民就普遍使用算筹进行计数.
算筹计数法就是用一根根同样长短和粗细的小棍子(用竹子、木头、兽骨、象牙、
金属等材料制成)以不同的排列方式来表示数字,如图所示.如果用算筹随机摆
出一个不含数字 0的两位数,个位用纵式,十位用横式,则个位和十位上的算筹
一样多的概率为( )
A. B. C. D.
8. 函数 在 上的图象大致为( )
A. B. C. D.
二、多选题
9. 函数 的定义域为 ,它的导函数 的部分图象如图所示,则下列
结论正确的是( )
A.函数 有三个极值点 B.
C.函数 在 上单调递增 D. 是 的极小值点
10. 若函数 在 上单调递减,则实数 a 值可能为( )
A. B.1 C. D.4
11. 若 ,则下列结论正确的是( )
A. B.
C. D.
三、填空题
12. 已知随机变量 的分布列如下表,若 ,则 a=________, ______.
0 1 2
P a b
13. 某数学兴趣小组的 5名学生负责讲述“宋元数学四大家”——秦九韶、李冶、
杨辉和朱世杰的故事,每名学生只讲一个数学家的故事,每个数学家的故事都有
学生讲述,则不同的分配方案有______种.
14. 的展开式中,常数项为__________.
四、解答题
15. 已知口袋中有 2个白球和 4个红球,现从中随机抽取两次,每次抽取 1个.
(1)若采取放回的方法连续抽取两次,求两次都取得白球的概率;
(2)若采取不放回的方法连续抽取两次,求两次至少有一次取得白球的概率;
(3)若采取不放回的方法连续抽取两次,求在第一次取出红球的条件下,第二次
取出的是红球的概率.
16. 已知函数 .
(1)求函数 的单调区间;
(2)求函数 在区间 中的最大值.
17. 已知 的二项展开式有 7项.
(1)求 ,并求出所有二项式系数之和;
(2)求展开式中含 项的系数;
(3)求展开式中的有理项.
18. 当前,以 ChatGPT 为代表的 AIGC(利用 AI 技术自动生成内容的生产方式)
领域一系列创新技术有了革命性突破,全球各大科技企业都在积极拥抱 AIGC,
我国的 BAT(百度、阿里、腾讯 3个企业的简称)、字节跳动、万兴科技、蓝色
光标、华为等领头企业已纷纷加码布局 AIGC 赛道,某传媒公司准备发布《2023
年中国 AIGC 发展研究报告》,先期准备从上面 7个科技企业中随机选取 3个进行
采访.
(1)求选取的 3个科技企业中,BAT 中至多有 1个的概率;
(2)记选取的 3个科技企业中 BAT 中的个数为 ,求 的分布列与期望.
19. 已知函数 .
(1)若曲线 在点 处的切线与 轴平行,求实数 的值;
(2)若函数 在 内存在极值,求实数 的取值范围;
(3)若对任意的实数 , 恒成立,求实数 的取值范围.
广东省清远市清新区第三中学 2024-2025 学年高二下学期期中考试数学试题
整体难度:适中
考试范围:计数原理与概率统计、函数与导数、等式与不等式
试卷题型
题型 数量
单选题 8
多选题 3
填空题 3
解答题 5
试卷难度
难度 题数
容易 5
较易 5
适中 8
较难 1
细目表分析
题号 难度系数 详细知识点
一、单选题
1 0.94 离散型随机变量与连续型随机变量的区分;判断随机试验中的随机变量
2 0.94 基本初等函数的导数公式
3 0.94 求某点处的导数值
4 0.94 求在曲线上一点处的切线方程(斜率)
5 0.94 求已知函数的极值
6 0.65 计算条件概率;利用全概率公式求概率
7 0.85 计算古典概型问题的概率;分类加法计数原理;分步乘法计数原理及简单应用
函数奇偶性的定义与判断;用导数判断或证明已知函数的单调性;函数图像的识
8 0.65
别
二、多选题
9 0.85 函数与导函数图象之间的关系;函数(导函数)图像与极值点的关系
10 0.65 由函数在区间上的单调性求参数;对勾函数求最值
11 0.65 求指定项的系数;二项展开式各项的系数和
三、填空题
12 0.85 离散型随机变量的方差与标准差;由离散型随机变量的均值求参数
13 0.65 全排列问题;分组分配问题;分步乘法计数原理及简单应用;排列组合综合
14 0.65 三项展开式的系数问题
四、解答题
15 0.65 计算条件概率;独立事件的乘法公式;利用对立事件的概率公式求概率
16 0.85 利用导数求函数的单调区间(不含参);由导数求函数的最值(不含参)
17 0.65 求指定项的系数;求有理项或其系数;二项式的系数和
写出简单离散型随机变量分布列;求离散型随机变量的均值;实际问题中的组合
18 0.85
计数问题;计算古典概型问题的概率
根据极值求参数;利用导数研究不等式恒成立问题;已知切线(斜率)求参数;
19 0.4
利用导数研究函数的零点
知识点分析
序号 知识点 对应题号
1 计数原理与概率统计 1,6,7,11,12,13,14,15,17,18
2 函数与导数 2,3,4,5,8,9,10,16,19
3 等式与不等式 10
试题答案解析
第 1题:
第 2题:
第 3题:
第 4题:
第 5题:
第 6题:
第 7题:
第 8题:
第 9题:
第 10 题:
第 11 题:
第 12 题:
第 13 题:
第 14 题:
第 15 题:
第 16 题:
第 17 题:
第 18 题:
第 19 题:
同课章节目录
