期中评估测试卷(含答案) 2025-2026学年数学人教版(2024)八年级上册
文档属性
| 名称 | 期中评估测试卷(含答案) 2025-2026学年数学人教版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 536.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-31 21:36:27 | ||
图片预览

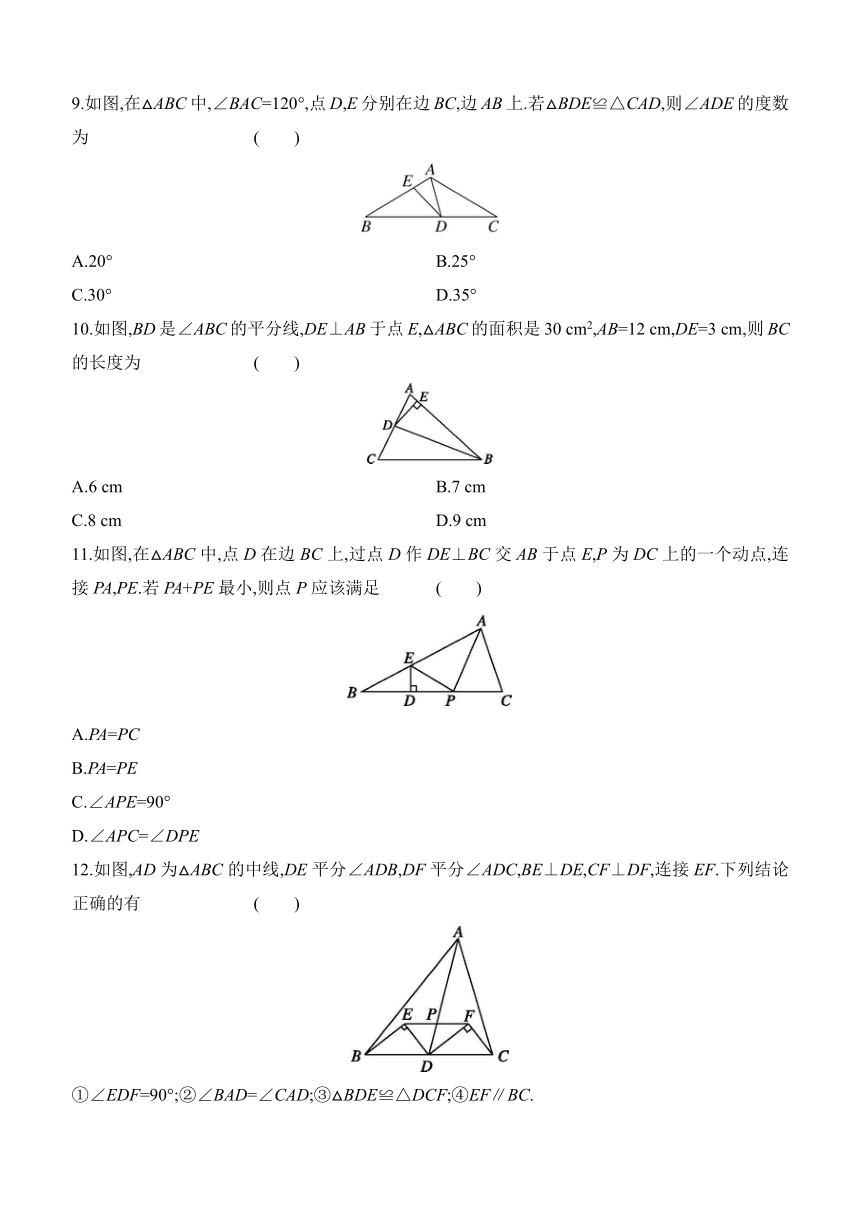


文档简介
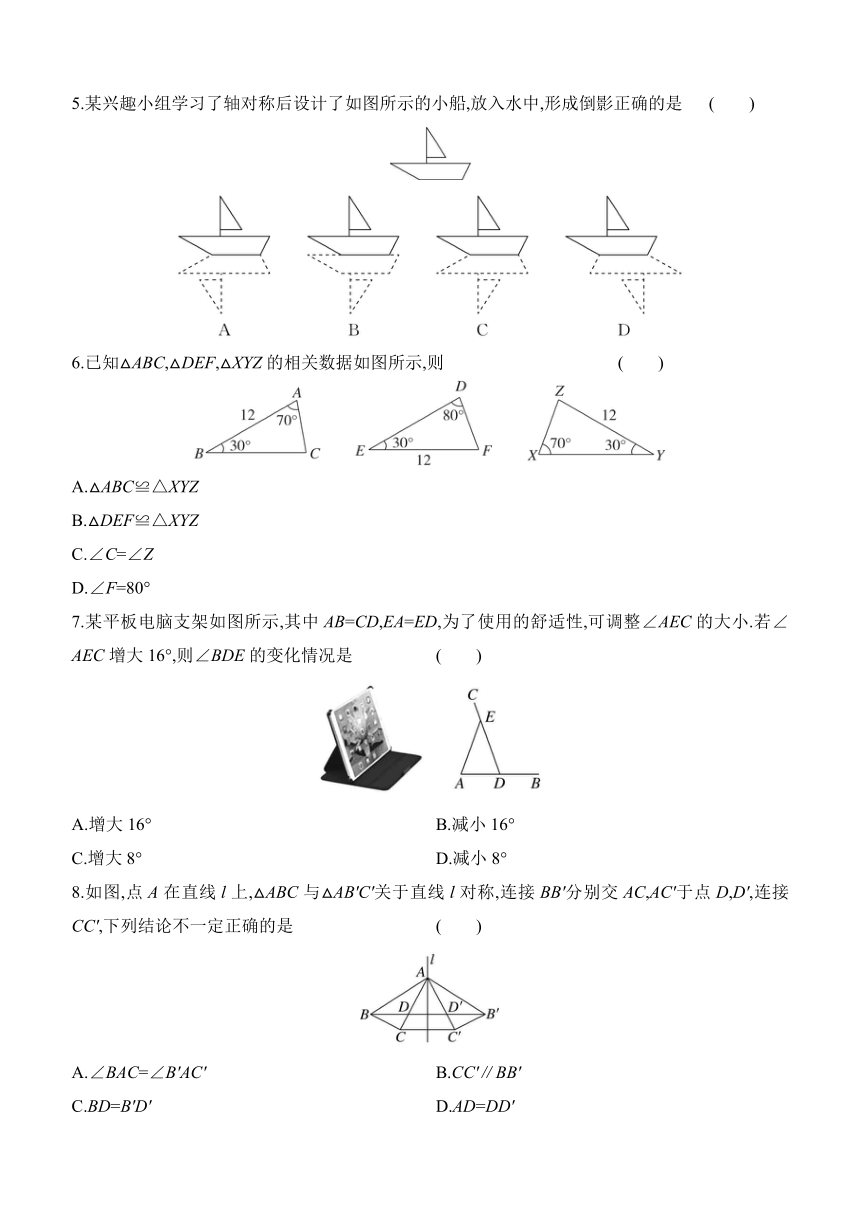
期中评估测试卷
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024扬州中考)“致中和,天地位焉,万物育焉”,对称之美随处可见.下列选项分别是扬州大学、扬州中国大运河博物馆、扬州五亭桥、扬州志愿服务的标识,其中的轴对称图形是 ( )
2.如图,图中三角形的个数有 ( )
A.6 B.8
C.10 D.12
3.生活中,如图所示的情况,在电线杆上拉两条钢缆,来加固电线杆,这是利用了三角形的 ( )
A.稳定性 B.全等性
C.灵活性 D.对称性
4.(2025邯郸丛台区期中)绝缘梯是电力工程的专用登高工具,如图,绝缘梯模型中OA,OB的长度都为2 m,则A,B两点之间的距离可能是 ( )
A.3 m B.4 m
C.4.5 m D.5 m
5.某兴趣小组学习了轴对称后设计了如图所示的小船,放入水中,形成倒影正确的是 ( )
6.已知△ABC,△DEF,△XYZ的相关数据如图所示,则 ( )
A.△ABC≌△XYZ
B.△DEF≌△XYZ
C.∠C=∠Z
D.∠F=80°
7.某平板电脑支架如图所示,其中AB=CD,EA=ED,为了使用的舒适性,可调整∠AEC的大小.若∠AEC增大16°,则∠BDE的变化情况是 ( )
A.增大16° B.减小16°
C.增大8° D.减小8°
8.如图,点A在直线l上,△ABC与△AB'C'关于直线l对称,连接BB'分别交AC,AC'于点D,D',连接CC',下列结论不一定正确的是 ( )
A.∠BAC=∠B'AC' B.CC'∥BB'
C.BD=B'D' D.AD=DD'
9.如图,在△ABC中,∠BAC=120°,点D,E分别在边BC,边AB上.若△BDE≌△CAD,则∠ADE的度数为 ( )
A.20° B.25°
C.30° D.35°
10.如图,BD是∠ABC的平分线,DE⊥AB于点E,△ABC的面积是30 cm2,AB=12 cm,DE=3 cm,则BC的长度为 ( )
A.6 cm B.7 cm
C.8 cm D.9 cm
11.如图,在△ABC中,点D在边BC上,过点D作DE⊥BC交AB于点E,P为DC上的一个动点,连接PA,PE.若PA+PE最小,则点P应该满足 ( )
A.PA=PC
B.PA=PE
C.∠APE=90°
D.∠APC=∠DPE
12.如图,AD为△ABC的中线,DE平分∠ADB,DF平分∠ADC,BE⊥DE,CF⊥DF,连接EF.下列结论正确的有 ( )
①∠EDF=90°;②∠BAD=∠CAD;③△BDE≌△DCF;④EF∥BC.
A.4个 B.3个
C.2个 D.1个
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2025淄博月考)如图,已知AB=DE,∠A=∠D,请你添加一个条件(一个即可): ,使△ABC≌△DEC.
14.若等腰三角形的腰长为2.5,顶角为60°,则这个等腰三角形的周长为 .
15.如图,在△ABC中,AB的垂直平分线交AC于点D.若△BCD的周长为5,BC=2,则AC的长为 ,边AB长的取值范围是 .
16.如图,AF和AD分别是△ABC的高和角平分线,且∠B=35°,∠C=75°,则∠BAC= ,
∠DAF= .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,A,B是两个村庄,CD是一条暗河露出地面的部分.两村村民想要建一个蓄水池,使它到A,B两个村庄的距离相等,并且到暗河两端C,D的距离也相等.请帮助他们找到符合这个要求的位置.(尺规作图,保留作图痕迹,不写作法)
18.(8分)如图,在平面直角坐标系中,A(0,-2),B(2,-4),C(4,-1).
(1)画出与△ABC关于y轴对称的图形△A1B1C1.
(2)写出△A1B1C1各顶点坐标:A1( , ),B1( , ),C1( , ).
(3)求△ABC的面积.
19.(8分)如图,在三角形纸片中,AB=8 cm,BC=6 cm,AC=5 cm.沿过点B的直线折叠这个三角形,使点C落在边AB上的点E处,折痕为BD,求△ADE的周长.
20.(8分)如图,在△ABC中,DE是AC的垂直平分线,∠B=∠ADB.
(1)求证:AB=CD.
(2)若∠C=30°,AB=6,求DE的长.
21.(8分)在△ABC中,AF平分∠BAC,CD⊥AF,垂足为F,CD与AB交于点D.
(1)如图1,若∠BAC=80°,∠B=40°,则∠BCD的度数为 °.
(2)如图2,在△ABC内部作∠ACE=∠B.求证:∠BCD=∠DCE.
22.(10分)如图,在△ABC中,∠C=90°,∠A=30°,AB=60 cm,动点P,Q同时从A,B两点出发,分别在AB, BC边上匀速移动,它们的速度分别为vP=2 cm/s,vQ=1 cm/s,当点P到达点B时,P,Q两点同时停止运动,设点P的运动时间为t s.
(1)当t为何值时,△PBQ为等边三角形
(2)当t为何值时,△PBQ为直角三角形
23.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,D是边AC上一点,连接BD,EC⊥AC,且AE=BD,AE与BC交于点F.
(1)求证:CE=AD.
(2)当AD=CF时,求证:BD平分∠ABC.
24.(12分)在等边三角形ABC中,D是直线BC上的一个点(不与点B,C重合),以AD为边在AD右侧作等边三角形ADE,连接CE.
(1)如图1,当点D在线段BC上时,求证:BD=CE.
(2)如图2,当点D在线段BC的反向延长线上时,若∠BAE=α,求∠DEC的度数(用含α的式子表示).
(3)如图3,当点D在线段BC的延长线上时,若BD⊥DE,且S△ABC=4,求△ACF的面积.
【详解答案】
1.C 2.B 3.A 4.A 5.C 6.C
7.D 解析:∵EA=ED,∴∠EAD=∠EDA,∴∠AEC=∠EAD+∠ADE=2∠ADE,∵∠AEC增大16°,∴∠ADE增大8°,∵∠BDE=180°-∠ADE,∴∠BDE减小8°.故选D.
8.D 解析:如图,∵△ABC与△AB'C'关于直线l对称,∴△ABC≌△AB'C',BB'⊥l,CC'⊥l,AB=AB',AC=AC',∴∠BAC =∠B'AC',BB'∥CC',∴OD=OD',OB=OB',∴BD=B'D',故选项A,B,C正确.故选D.
9.C 解析:∵△BDE≌△CAD,∴∠B=∠C,∠BDE=∠CAD,∵∠BAC=120°,∴∠C=×(180°-120°)=30°,∵∠BDE+∠ADE=∠C+∠CAD,∴∠ADE=∠C=30°.故选C.
10.C 解析:如图,过点D作DF⊥BC,垂足为F.∵BD是∠ABC的平分线,DE⊥AB,∴DE=DF=3 cm.∵△ABC的面积是30 cm2,S△ABC=S△BDC+S△BDA,∴S△ABC=BC·DF+AB·DE=·(BC+12)=30.∴BC=8 cm.故选C.
11.D 解析:如图,作点E关于直线BC的对称点F,连接AF交BC于点P,此时PA+PE最小.由对称性可知,
∠DPE=∠FPD.∵∠APC=∠FPD,∴∠APC=∠DPE.∴PA+PE最小时,点P应该满足∠APC=∠DPE.故选D.
12.B 解析:∵DE平分∠ADB,DF平分∠ADC,∴∠ADE=∠ADB,∠ADF=∠ADC.∴∠EDF=∠ADE+∠ADF =(∠ADB+∠ADC)=90°.故①符合题意;∵AD为△ABC的中线,∴BD=CD.而∠BAD与∠CAD不一定相等,故②不符合题意;∵BE⊥DE,CF⊥DF,∴∠BED=∠DFC=90°.∴∠EBD+∠EDB=90°.∵∠EDF=90°,∴∠EDB+∠FDC =90°.∴∠EBD=∠FDC.∵∠BED=∠DFC,BD=DC,∴△BDE≌△DCF(AAS).故③符合题意;∵△BDE≌△DCF,∴∠EDB=∠FCD,ED=FC,BE=DF.∴△DCF可看作是△BDE沿BD平移得到的.∴EF∥BC.故④符合题意.综上所述,正确的有①③④,共3个.故选B.
13.AC=DC(答案不唯一)
14.7.5
15.3 116.70° 20° 解析:在△ABC中,∠B=35°,∠C=75°,∴∠BAC=180°-∠B-∠C=180°-35°-75°=70°.∵AD是△ABC的角平分线,∴∠DAC=∠BAC=×70°=35°.∵AF是△ABC的高,∴∠AFC=90°.∴∠FAC=90°-∠C=90°-75°=15°.
∴∠DAF=∠DAC-∠FAC=35°-15°=20°.
17.解:如图,点P即为所求.
18.解:(1)如图所示,△A1B1C1即为所求.
(2)0 -2 -2 -4 -4 -1
(3)△ABC的面积=3×4-×1×4-×2×2-×2×3=5.
19.解:∵BC沿BD折叠,点C落在边AB上的点E处,
∴DE=DC,BE=BC.
∵AB=8 cm,BC=6 cm,
∴AE=AB-BE=AB-BC=8-6=2(cm).
∴△ADE的周长为AD+DE+AE=AD+DC+AE=AC+AE=5+2=7(cm).
20.解:(1)证明:∵DE是AC的垂直平分线,
∴AD=CD,
∵∠B=∠ADB,∴AB=AD,∴AB=CD.
(2)由(1)可知,AB=CD,
∴CD=AB=6,
∵DE是AC的垂直平分线,∠C=30°,
∴DE⊥AC,
∴∠DEC=90°,
∴DE=DC=3.
21.解:(1)10
(2)证明:∵AF平分∠BAC,
∴∠DAF=∠CAF.
∵CD⊥AF,∴∠AFD=∠AFC=90°.
在△AFD中,∠DAF+∠ADF=90°,
在△AFC中,∠CAF+∠ACF=90°.
∵∠DAF=∠CAF,∴∠ADC=∠ACD.
∵∠ADC是△BCD的一个外角,
∴∠ADC=∠B+∠BCD.
∵∠ACD=∠ACE+∠DCE,
∴∠B+∠BCD=∠ACE+∠DCE.
∵∠ACE=∠B,∴∠BCD=∠DCE.
22.解:(1)在△ABC中,∵∠C=90°,∠A=30°,∴∠B=90°-∠A=60°.
∵60÷2=30(s),
∴0≤t≤30,BP=(60-2t)cm,BQ=t cm.
当BP=BQ时,△PBQ为等边三角形,即60-2t=t,
∴t=20.
∴当t为20时,△PBQ为等边三角形.
(2)若△PBQ为直角三角形,
①当∠BQP=90°时,∵∠B=60°,
∴∠BPQ=90°-∠B=30°.
∴BP=2BQ,即60-2t=2t.∴t=15.
②当∠BPQ=90°时,∵∠B=60°,
∴∠PQB=90°-∠B=30°.
∴BQ=2BP,即t=2(60-2t).∴t=24.
∴当t为15或24时,△PBQ为直角三角形.
23.证明:(1)∵EC⊥AC,∴∠ACE=90°.
在Rt△CAE和Rt△ABD中,
∴Rt△CAE≌Rt△ABD(HL).
∴CE=AD.
(2)如图,设AE与BD交于点G.
由(1)得Rt△CAE≌Rt△ABD,
∴∠EAC=∠DBA,∠E=∠ADB,CE=AD.
∵AD=CF,∴CE=CF.∴∠E=∠CFE.
∵∠CFE=∠AFB,∴∠AFB=∠E.
∵∠E=∠ADB,∴∠AFB=∠ADB.
∵∠AGB=∠EAC+∠ADB,∠AGB=∠DBC+∠AFB,
∴∠EAC=∠DBC.
∵∠EAC=∠DBA,∴∠DBA=∠DBC.
∴BD平分∠ABC.
24.解:(1)证明:∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).∴BD=CE.
(2)如图,设AE交CD于点O.
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE.
∵△ABC,△ADE都是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,∠AED=60°.
∴∠ABD=180°-∠ABC=120°.
∴∠ACE=120°.
∴∠DCE=∠ACE-∠ACB=60°.
∵∠AOC=∠DOE,∠ACO=∠DEO=60°,
∴∠EDC=∠CAO=∠BAC-∠BAE=60°-α.
∴∠DEC=180°-∠EDC-∠DCE=180°-(60°-α)-60°=60°+α.
(3)∵△ABC,△ADE都是等边三角形,
∴∠ACB=∠B=∠ADE=60°,AC=BC,AE=AD.
∵BD⊥DE,∴∠EDB=90°.
∴∠ADB=90°-60°=30°.
∴∠BAD=180°-∠B-∠ADB=90°.
∵∠ACB=∠CAD+∠CDA=60°,
∴∠CAD=60°-30°=30°.
∴∠CAD=∠CDA.∴CA=CD.
∴CB=CD.∴S△ACD=S△ABC=4.
∵EA=ED,CA=CD,
∴点E,C都在线段AD的垂直平分线上.
∴CE垂直平分线段AD.
∴AF=DF.∴S△ACF=S△ACD=2.
(总分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024扬州中考)“致中和,天地位焉,万物育焉”,对称之美随处可见.下列选项分别是扬州大学、扬州中国大运河博物馆、扬州五亭桥、扬州志愿服务的标识,其中的轴对称图形是 ( )
2.如图,图中三角形的个数有 ( )
A.6 B.8
C.10 D.12
3.生活中,如图所示的情况,在电线杆上拉两条钢缆,来加固电线杆,这是利用了三角形的 ( )
A.稳定性 B.全等性
C.灵活性 D.对称性
4.(2025邯郸丛台区期中)绝缘梯是电力工程的专用登高工具,如图,绝缘梯模型中OA,OB的长度都为2 m,则A,B两点之间的距离可能是 ( )
A.3 m B.4 m
C.4.5 m D.5 m
5.某兴趣小组学习了轴对称后设计了如图所示的小船,放入水中,形成倒影正确的是 ( )
6.已知△ABC,△DEF,△XYZ的相关数据如图所示,则 ( )
A.△ABC≌△XYZ
B.△DEF≌△XYZ
C.∠C=∠Z
D.∠F=80°
7.某平板电脑支架如图所示,其中AB=CD,EA=ED,为了使用的舒适性,可调整∠AEC的大小.若∠AEC增大16°,则∠BDE的变化情况是 ( )
A.增大16° B.减小16°
C.增大8° D.减小8°
8.如图,点A在直线l上,△ABC与△AB'C'关于直线l对称,连接BB'分别交AC,AC'于点D,D',连接CC',下列结论不一定正确的是 ( )
A.∠BAC=∠B'AC' B.CC'∥BB'
C.BD=B'D' D.AD=DD'
9.如图,在△ABC中,∠BAC=120°,点D,E分别在边BC,边AB上.若△BDE≌△CAD,则∠ADE的度数为 ( )
A.20° B.25°
C.30° D.35°
10.如图,BD是∠ABC的平分线,DE⊥AB于点E,△ABC的面积是30 cm2,AB=12 cm,DE=3 cm,则BC的长度为 ( )
A.6 cm B.7 cm
C.8 cm D.9 cm
11.如图,在△ABC中,点D在边BC上,过点D作DE⊥BC交AB于点E,P为DC上的一个动点,连接PA,PE.若PA+PE最小,则点P应该满足 ( )
A.PA=PC
B.PA=PE
C.∠APE=90°
D.∠APC=∠DPE
12.如图,AD为△ABC的中线,DE平分∠ADB,DF平分∠ADC,BE⊥DE,CF⊥DF,连接EF.下列结论正确的有 ( )
①∠EDF=90°;②∠BAD=∠CAD;③△BDE≌△DCF;④EF∥BC.
A.4个 B.3个
C.2个 D.1个
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(2025淄博月考)如图,已知AB=DE,∠A=∠D,请你添加一个条件(一个即可): ,使△ABC≌△DEC.
14.若等腰三角形的腰长为2.5,顶角为60°,则这个等腰三角形的周长为 .
15.如图,在△ABC中,AB的垂直平分线交AC于点D.若△BCD的周长为5,BC=2,则AC的长为 ,边AB长的取值范围是 .
16.如图,AF和AD分别是△ABC的高和角平分线,且∠B=35°,∠C=75°,则∠BAC= ,
∠DAF= .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)如图,A,B是两个村庄,CD是一条暗河露出地面的部分.两村村民想要建一个蓄水池,使它到A,B两个村庄的距离相等,并且到暗河两端C,D的距离也相等.请帮助他们找到符合这个要求的位置.(尺规作图,保留作图痕迹,不写作法)
18.(8分)如图,在平面直角坐标系中,A(0,-2),B(2,-4),C(4,-1).
(1)画出与△ABC关于y轴对称的图形△A1B1C1.
(2)写出△A1B1C1各顶点坐标:A1( , ),B1( , ),C1( , ).
(3)求△ABC的面积.
19.(8分)如图,在三角形纸片中,AB=8 cm,BC=6 cm,AC=5 cm.沿过点B的直线折叠这个三角形,使点C落在边AB上的点E处,折痕为BD,求△ADE的周长.
20.(8分)如图,在△ABC中,DE是AC的垂直平分线,∠B=∠ADB.
(1)求证:AB=CD.
(2)若∠C=30°,AB=6,求DE的长.
21.(8分)在△ABC中,AF平分∠BAC,CD⊥AF,垂足为F,CD与AB交于点D.
(1)如图1,若∠BAC=80°,∠B=40°,则∠BCD的度数为 °.
(2)如图2,在△ABC内部作∠ACE=∠B.求证:∠BCD=∠DCE.
22.(10分)如图,在△ABC中,∠C=90°,∠A=30°,AB=60 cm,动点P,Q同时从A,B两点出发,分别在AB, BC边上匀速移动,它们的速度分别为vP=2 cm/s,vQ=1 cm/s,当点P到达点B时,P,Q两点同时停止运动,设点P的运动时间为t s.
(1)当t为何值时,△PBQ为等边三角形
(2)当t为何值时,△PBQ为直角三角形
23.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,D是边AC上一点,连接BD,EC⊥AC,且AE=BD,AE与BC交于点F.
(1)求证:CE=AD.
(2)当AD=CF时,求证:BD平分∠ABC.
24.(12分)在等边三角形ABC中,D是直线BC上的一个点(不与点B,C重合),以AD为边在AD右侧作等边三角形ADE,连接CE.
(1)如图1,当点D在线段BC上时,求证:BD=CE.
(2)如图2,当点D在线段BC的反向延长线上时,若∠BAE=α,求∠DEC的度数(用含α的式子表示).
(3)如图3,当点D在线段BC的延长线上时,若BD⊥DE,且S△ABC=4,求△ACF的面积.
【详解答案】
1.C 2.B 3.A 4.A 5.C 6.C
7.D 解析:∵EA=ED,∴∠EAD=∠EDA,∴∠AEC=∠EAD+∠ADE=2∠ADE,∵∠AEC增大16°,∴∠ADE增大8°,∵∠BDE=180°-∠ADE,∴∠BDE减小8°.故选D.
8.D 解析:如图,∵△ABC与△AB'C'关于直线l对称,∴△ABC≌△AB'C',BB'⊥l,CC'⊥l,AB=AB',AC=AC',∴∠BAC =∠B'AC',BB'∥CC',∴OD=OD',OB=OB',∴BD=B'D',故选项A,B,C正确.故选D.
9.C 解析:∵△BDE≌△CAD,∴∠B=∠C,∠BDE=∠CAD,∵∠BAC=120°,∴∠C=×(180°-120°)=30°,∵∠BDE+∠ADE=∠C+∠CAD,∴∠ADE=∠C=30°.故选C.
10.C 解析:如图,过点D作DF⊥BC,垂足为F.∵BD是∠ABC的平分线,DE⊥AB,∴DE=DF=3 cm.∵△ABC的面积是30 cm2,S△ABC=S△BDC+S△BDA,∴S△ABC=BC·DF+AB·DE=·(BC+12)=30.∴BC=8 cm.故选C.
11.D 解析:如图,作点E关于直线BC的对称点F,连接AF交BC于点P,此时PA+PE最小.由对称性可知,
∠DPE=∠FPD.∵∠APC=∠FPD,∴∠APC=∠DPE.∴PA+PE最小时,点P应该满足∠APC=∠DPE.故选D.
12.B 解析:∵DE平分∠ADB,DF平分∠ADC,∴∠ADE=∠ADB,∠ADF=∠ADC.∴∠EDF=∠ADE+∠ADF =(∠ADB+∠ADC)=90°.故①符合题意;∵AD为△ABC的中线,∴BD=CD.而∠BAD与∠CAD不一定相等,故②不符合题意;∵BE⊥DE,CF⊥DF,∴∠BED=∠DFC=90°.∴∠EBD+∠EDB=90°.∵∠EDF=90°,∴∠EDB+∠FDC =90°.∴∠EBD=∠FDC.∵∠BED=∠DFC,BD=DC,∴△BDE≌△DCF(AAS).故③符合题意;∵△BDE≌△DCF,∴∠EDB=∠FCD,ED=FC,BE=DF.∴△DCF可看作是△BDE沿BD平移得到的.∴EF∥BC.故④符合题意.综上所述,正确的有①③④,共3个.故选B.
13.AC=DC(答案不唯一)
14.7.5
15.3 1
∴∠DAF=∠DAC-∠FAC=35°-15°=20°.
17.解:如图,点P即为所求.
18.解:(1)如图所示,△A1B1C1即为所求.
(2)0 -2 -2 -4 -4 -1
(3)△ABC的面积=3×4-×1×4-×2×2-×2×3=5.
19.解:∵BC沿BD折叠,点C落在边AB上的点E处,
∴DE=DC,BE=BC.
∵AB=8 cm,BC=6 cm,
∴AE=AB-BE=AB-BC=8-6=2(cm).
∴△ADE的周长为AD+DE+AE=AD+DC+AE=AC+AE=5+2=7(cm).
20.解:(1)证明:∵DE是AC的垂直平分线,
∴AD=CD,
∵∠B=∠ADB,∴AB=AD,∴AB=CD.
(2)由(1)可知,AB=CD,
∴CD=AB=6,
∵DE是AC的垂直平分线,∠C=30°,
∴DE⊥AC,
∴∠DEC=90°,
∴DE=DC=3.
21.解:(1)10
(2)证明:∵AF平分∠BAC,
∴∠DAF=∠CAF.
∵CD⊥AF,∴∠AFD=∠AFC=90°.
在△AFD中,∠DAF+∠ADF=90°,
在△AFC中,∠CAF+∠ACF=90°.
∵∠DAF=∠CAF,∴∠ADC=∠ACD.
∵∠ADC是△BCD的一个外角,
∴∠ADC=∠B+∠BCD.
∵∠ACD=∠ACE+∠DCE,
∴∠B+∠BCD=∠ACE+∠DCE.
∵∠ACE=∠B,∴∠BCD=∠DCE.
22.解:(1)在△ABC中,∵∠C=90°,∠A=30°,∴∠B=90°-∠A=60°.
∵60÷2=30(s),
∴0≤t≤30,BP=(60-2t)cm,BQ=t cm.
当BP=BQ时,△PBQ为等边三角形,即60-2t=t,
∴t=20.
∴当t为20时,△PBQ为等边三角形.
(2)若△PBQ为直角三角形,
①当∠BQP=90°时,∵∠B=60°,
∴∠BPQ=90°-∠B=30°.
∴BP=2BQ,即60-2t=2t.∴t=15.
②当∠BPQ=90°时,∵∠B=60°,
∴∠PQB=90°-∠B=30°.
∴BQ=2BP,即t=2(60-2t).∴t=24.
∴当t为15或24时,△PBQ为直角三角形.
23.证明:(1)∵EC⊥AC,∴∠ACE=90°.
在Rt△CAE和Rt△ABD中,
∴Rt△CAE≌Rt△ABD(HL).
∴CE=AD.
(2)如图,设AE与BD交于点G.
由(1)得Rt△CAE≌Rt△ABD,
∴∠EAC=∠DBA,∠E=∠ADB,CE=AD.
∵AD=CF,∴CE=CF.∴∠E=∠CFE.
∵∠CFE=∠AFB,∴∠AFB=∠E.
∵∠E=∠ADB,∴∠AFB=∠ADB.
∵∠AGB=∠EAC+∠ADB,∠AGB=∠DBC+∠AFB,
∴∠EAC=∠DBC.
∵∠EAC=∠DBA,∴∠DBA=∠DBC.
∴BD平分∠ABC.
24.解:(1)证明:∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).∴BD=CE.
(2)如图,设AE交CD于点O.
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE.
∵△ABC,△ADE都是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,∠AED=60°.
∴∠ABD=180°-∠ABC=120°.
∴∠ACE=120°.
∴∠DCE=∠ACE-∠ACB=60°.
∵∠AOC=∠DOE,∠ACO=∠DEO=60°,
∴∠EDC=∠CAO=∠BAC-∠BAE=60°-α.
∴∠DEC=180°-∠EDC-∠DCE=180°-(60°-α)-60°=60°+α.
(3)∵△ABC,△ADE都是等边三角形,
∴∠ACB=∠B=∠ADE=60°,AC=BC,AE=AD.
∵BD⊥DE,∴∠EDB=90°.
∴∠ADB=90°-60°=30°.
∴∠BAD=180°-∠B-∠ADB=90°.
∵∠ACB=∠CAD+∠CDA=60°,
∴∠CAD=60°-30°=30°.
∴∠CAD=∠CDA.∴CA=CD.
∴CB=CD.∴S△ACD=S△ABC=4.
∵EA=ED,CA=CD,
∴点E,C都在线段AD的垂直平分线上.
∴CE垂直平分线段AD.
∴AF=DF.∴S△ACF=S△ACD=2.
同课章节目录
