2025届高考物理一轮复习专项练:斜抛运动
文档属性
| 名称 | 2025届高考物理一轮复习专项练:斜抛运动 |  | |
| 格式 | docx | ||
| 文件大小 | 669.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-31 18:25:49 | ||
图片预览



文档简介
斜抛运动练习
一、单选题(本大题共8小题)
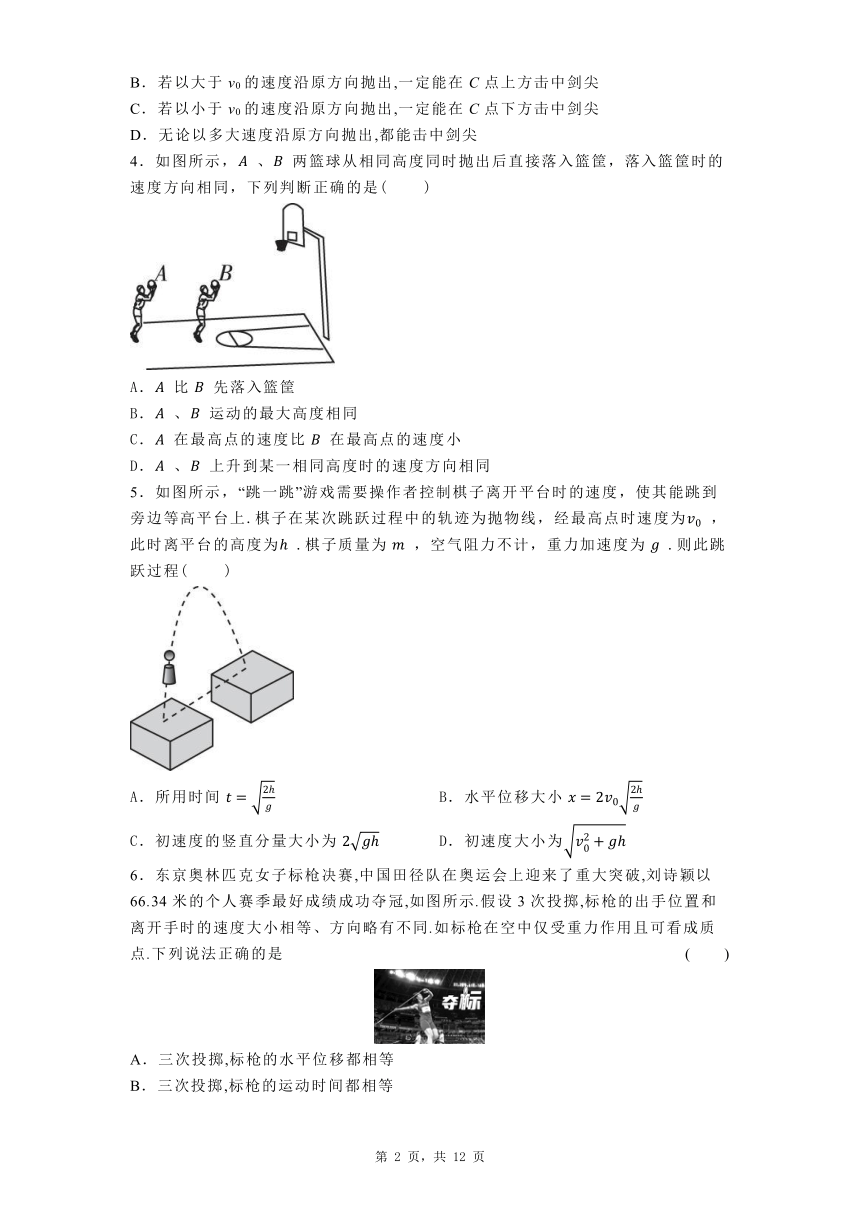
1.如图所示,乒乓球在球台上从O点弹起落在M点后,又弹起落在N点,不考虑乒乓球的旋转和空气阻力,则在上述两个过程中( )
A.运动时间相等
B.在最高点时加速度为零
C.在最高点时速度相等
D.在M点与台面碰撞前后速度大小相等
2.篮球是受大众喜爱的运动项目。如图所示,一同学将一篮球从地面上方 B 点斜向上与水平方向成 θ 角(即抛射角)抛出,刚好垂直击中篮板上 A 点,不计空气阻力.若该同学从抛射点 B 向远离篮板方向水平移动一小段距离,仍使抛出的篮球垂直击中 A 点,则可行的是( )
A.增大抛射角θ,同时减小抛出速度 v0
B.减小抛射角θ,同时增大抛射速度v0
C.增大抛射角θ,同时增大抛出速度v0
D.减小抛射角θ,同时减小抛射速度 v0
3.电视综艺节目《加油!向未来》中有一个橄榄球空中击剑游戏:宝剑从空中B点自由下落,同时橄榄球从A点以速度v0沿AB方向抛出,恰好在空中C点沿水平方向击中剑尖,不计空气阻力.关于橄榄球,下列说法正确的是 ( )
A.在空中运动的加速度大于宝剑下落的加速度
B.若以大于v0的速度沿原方向抛出,一定能在C点上方击中剑尖
C.若以小于v0的速度沿原方向抛出,一定能在C点下方击中剑尖
D.无论以多大速度沿原方向抛出,都能击中剑尖
4.如图所示, 、 两篮球从相同高度同时抛出后直接落入篮筐,落入篮筐时的速度方向相同,下列判断正确的是( )
A. 比 先落入篮筐
B. 、 运动的最大高度相同
C. 在最高点的速度比 在最高点的速度小
D. 、 上升到某一相同高度时的速度方向相同
5.如图所示,“跳一跳”游戏需要操作者控制棋子离开平台时的速度,使其能跳到旁边等高平台上.棋子在某次跳跃过程中的轨迹为抛物线,经最高点时速度为 ,此时离平台的高度为 .棋子质量为 ,空气阻力不计,重力加速度为 .则此跳跃过程( )
A.所用时间 B.水平位移大小
C.初速度的竖直分量大小为 D.初速度大小为
6.东京奥林匹克女子标枪决赛,中国田径队在奥运会上迎来了重大突破,刘诗颖以66.34米的个人赛季最好成绩成功夺冠,如图所示.假设3次投掷,标枪的出手位置和离开手时的速度大小相等、方向略有不同.如标枪在空中仅受重力作用且可看成质点.下列说法正确的是 ( )
A.三次投掷,标枪的水平位移都相等
B.三次投掷,标枪的运动时间都相等
C.如忽略刘诗颖投掷标枪时出手点离地高度,当投掷方向与水平方向等于37度角时水平位移最大
D.如忽略刘诗颖投掷标枪时出手点离地高度,当投掷方向与水平方向等于45度角时水平位移最大
7.一学生用两个颜色不同的篮球做斜抛运动游戏,如图所示,第一次出手,红色篮球的初速度与竖直方向的夹角 ;第二次出手,橙色篮球的初速度与竖直方向的夹角 .两次出手的位置在同一竖直线上,结果两篮球正好到达相同的最高点 ,则红色篮球、橙色篮球运动的高度之比为( )
A. B. C. D.
8.如图所示, 、 两篮球从相同高度同时抛出后直接落入篮筐,落入篮筐时的速度方向相同,下列判断正确的是( )
A. 比 先落入篮筐
B. 、 运动的最大高度相同
C. 在最高点的速度比 在最高点的速度小
D. 、 上升到某一相同高度时的速度方向相同
二、多选题(本大题共3小题)
9.在某次骑车投球,比赛中,甲、乙两参赛者在沿规定直轨道匀速骑行过程中,将手中网球沿垂直于骑行方向水平抛向地面上的塑料筐中,如图,点是轨道上离框最近的点。甲以的速度骑行,在点将网球以相对于人的速度水平抛出,网球恰好落人筐中;乙以的速度骑行,在与甲的抛出点等高处将球水平抛出,要想将球投入筐中,乙参赛者应( )(不计空气阻力)
A.在到达点之后将球抛出
B.在到达点之前将球抛出
C.将球也以速度水平抛出
D.将球以大于的速度水平抛出
10.(多选)如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
A.沿路径1抛出的物体落地的速率最大
B.沿路径3抛出的物体在空中运动的时间最长
C.三个物体抛出时初速度的竖直分量相等
D.三个物体抛出时初速度的水平分量相等
11.(多选)如图所示,一个质量 的小球在光滑水平面上运动, 时刻小球经过坐标原点 ,速度方向与 轴正方向的夹角为 ,速度大小 ,此刻开始对小球施加一个沿 轴负方向的水平恒力 ,已知 .下列判断正确的是( )
A.此后小球运动的最小速度为 B.此后小球的速度先增大后减小
C.小球再次经过 轴所需的时间为 D.小球的运动轨迹应为抛物线
三、实验题(本大题共2小题)
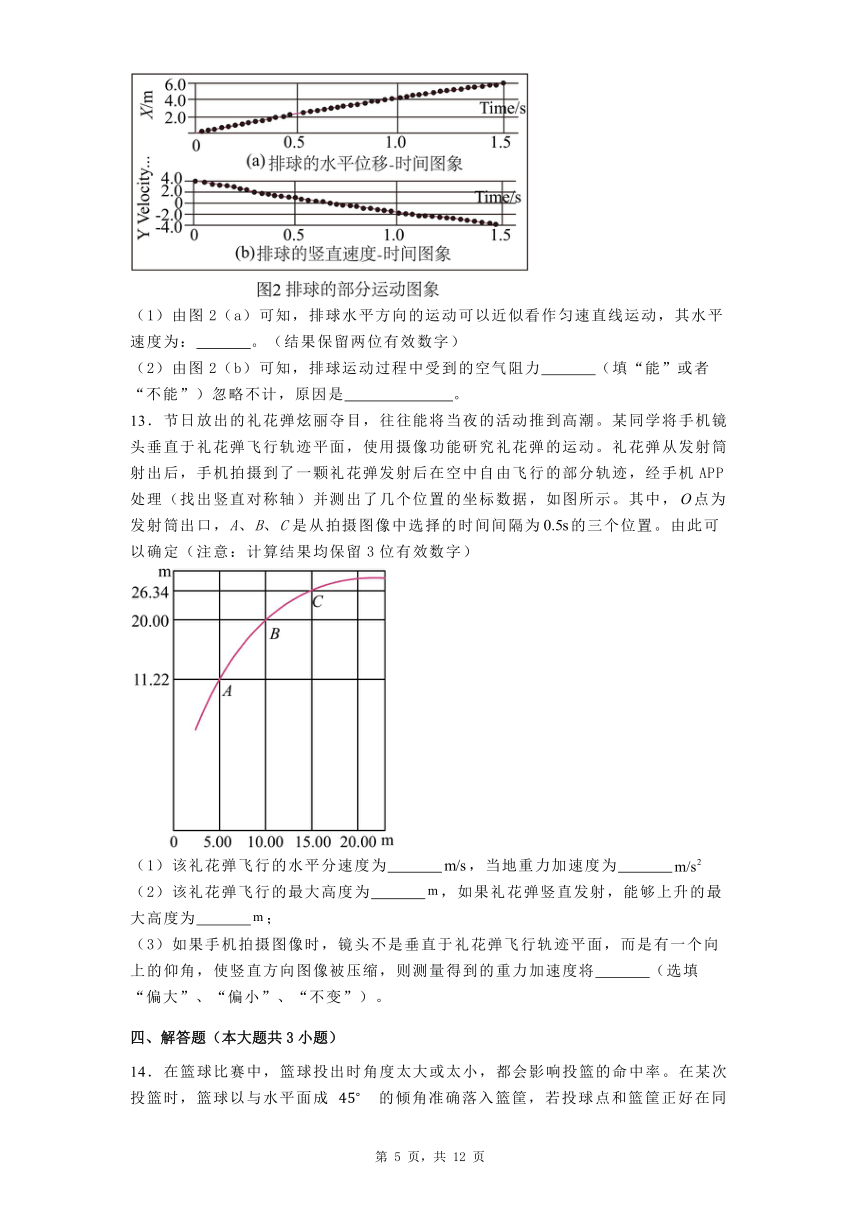
12.某物理兴趣小组借助视频分析软件来研究排球的运动。他们先从正面拍摄了一段排球运动的视频,在画面中建立直角坐标系,并选定排球网柱作为比例尺,这样画面中所有对象的位置信息就可以被定量记录下来,接着,在分析软件中将拍摄好的视频按照设定的时间间隔逐帧播放,那么每帧画面所对应的时间信息也就确定下来了,基于此,他们得到了排球运动的相关图像,如图所示。已知当地的重力加速速度为g=9.8m/s2。
(1)由图2(a)可知,排球水平方向的运动可以近似看作匀速直线运动,其水平速度为: 。(结果保留两位有效数字)
(2)由图2(b)可知,排球运动过程中受到的空气阻力 (填“能”或者“不能”)忽略不计,原因是 。
13.节日放出的礼花弹炫丽夺目,往往能将当夜的活动推到高潮。某同学将手机镜头垂直于礼花弹飞行轨迹平面,使用摄像功能研究礼花弹的运动。礼花弹从发射筒射出后,手机拍摄到了一颗礼花弹发射后在空中自由飞行的部分轨迹,经手机APP处理(找出竖直对称轴)并测出了几个位置的坐标数据,如图所示。其中,点为发射筒出口,A、B、C是从拍摄图像中选择的时间间隔为的三个位置。由此可以确定(注意:计算结果均保留3位有效数字)
(1)该礼花弹飞行的水平分速度为 ,当地重力加速度为
(2)该礼花弹飞行的最大高度为 ,如果礼花弹竖直发射,能够上升的最大高度为 ;
(3)如果手机拍摄图像时,镜头不是垂直于礼花弹飞行轨迹平面,而是有一个向上的仰角,使竖直方向图像被压缩,则测量得到的重力加速度将 (选填“偏大”、“偏小”、“不变”)。
四、解答题(本大题共3小题)
14.在篮球比赛中,篮球投出时角度太大或太小,都会影响投篮的命中率。在某次投篮时,篮球以与水平面成 的倾角准确落入篮筐,若投球点和篮筐正好在同一水平面上(如图所示),投球点到篮筐距离为 ,不考虑空气阻力,重力加速度 取 。求:
(1)篮球运动至最高点时速度 的大小;
(2)篮球在空中运动的时间t;
(3)篮球运动中的最高位置相对篮筐的竖直高度 。
15.[山东潍坊诸城、安丘、高密2023高一下期中](15分)水平地面上有一足够长的固定斜面,倾角为37°,小华站在斜面底端向斜面上投郑小石子。若小石子出手时的初速度方向与水平方向成45°,出手高度为站立点正上方处,小石子的飞行轨迹所在平面与斜面底边垂直,落在斜面上时速度方向恰好水平。已知站立点到落点的距离为,重力加速度,,,不计空气阻力。求:
(1)小石子在空中的飞行时间;
(2)小石子出手时初速度的大小。
16.(16分)抛体运动在各类体育运动项目中都很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,如图所示.不考虑乒乓球的旋转和空气阻力(设重力加速度为g).
(1)若球在球台边缘O点正上方高度为h1处以速度v1水平发出,落在球台上的P1点(运动轨迹如图中实线所示),求P1点距O点的距离x1.
(2)若球在O点正上方以速度v2水平发出,经反弹恰好在最高点时越过球网落在球台上的P2点(运动轨迹如图中虚线所示),求v2的大小.
(3)若球在O点正上方水平发出后,经反弹恰好越过球网且刚好落在对方球台边缘P3处,求发球点距O点的高度h3.
参考答案
1.【答案】A
【详解】A.两次的高度相同,且每次从最高点到落在球台上做平抛运动,由公式可知,做平抛运动的时间相同,根据对称性可知,两次运动时间相等,故A正确;
B.在最高点时球还受到重力的作用,则加速度为重力加速度,故B错误;
C.由于运动时间相等,两次水平方向的位移不同,则水平方向的初速度不相同,说明在最高点时速度不相等,故C错误;
D.由于高度相等,由公式可知,在M点与台面碰撞前后竖直方向的速度大小相等,且初速度大小不同,由平行四边形定则可知,在M点与台面碰撞前后速度大小不相等,故D错误。
故选A。
2.【答案】B
【详解】由于篮球垂直击中A点,其逆过程是平抛运动,抛射点B向远离篮板方向水平移动一小段距离,由于平抛运动的高度不变,运动时间不变,水平位移变大,初速度变大。落地时水平速度变大,竖直速度不变,则落地速度方向与水平面的夹角变小。因此只有减小抛射角,同时增大抛出速度,才能仍垂直打到篮板上。故B正确,ACD错误。
故选B。
3.【答案】B
【解析】橄榄球在空中做斜抛运动,其在空中运动的加速度等于宝剑下落的加速度,选项A错误;当橄榄球的初速度大于v0时,水平方向分速度增加,而水平方向位移不变,所以时间减小,宝剑从B点下落的距离减小,橄榄球肯定在C点上方击中剑尖,选项B正确;如果橄榄球的初速度小于v0,宝剑落地时橄榄球水平方向位移可能小于A点到BC的水平距离,此时不能击中剑尖,选项C、D错误.
4.【答案】D
【详解】根据逆向思维,假设篮球从篮筐中做斜抛运动回到手中,由题分析, 回到手中时,水平距离要远,由抛出的速度方向相同可知, 水平方向速度比 水平方向速度大,在最高点只有水平速度,即 在最高点的速度比 在最高点的速度大,C错误;由速度的分解可知, 抛出的速度比 抛出的速度大,则 起抛时竖直方向的速度比 的大,上升到的最高点比 高,B错误; 上升的时间比 长,且两球从最高点落到相同高度的手中时,根据竖直方向做自由落体运动可知, 下落的时间比 长,所以 比 晚落入篮筐,A错误;在 、 球斜抛轨迹上作篮筐位置的等高线,在实际抛出篮球上升过程中,根据斜抛运动的对称性, 、 两位置处的速度方向相同,D正确.
【关键点拨】解答本题的关键是将斜抛运动的上升过程看作逆向的平抛运动,利用平抛运动规律分析判断.
5.【答案】B
【详解】竖直方向,由 ,可得 ,该斜抛运动等效为两个完全相同的平抛运动,时间是 ,A错误;水平位移 ,B正确;初速度的竖直分量大小 ,C错误;初速度大小 ,D错误.
6.【答案】D
【解析】设标枪离开手时的速度方向与水平方向夹角θ,则竖直方向有vy=vsin θ,设标枪的出手位置距离地面的高度为h,取向上为正方向,则运动的时间-h=vyt-gt2=(vsin θ)t-gt2,解得t=(另一个不符合题意舍掉),角度不同,时间不相等,水平位移x=(vcos θ)t可知水平位移不一定相等,A、B错误;根据竖直方向vy=vsin θ,则运动的时间t=2=,水平位移x=(vcos θ)t解得x=,知θ=45°时,sin2θ最大,则落地点和抛出点间的水平距离最大,C错误,D正确.
7.【答案】A
【详解】两个不同颜色的篮球做斜抛运动,到达相同的最高点,可将其逆运动看成水平向左的平抛运动,运动轨迹如图所示,两平抛运动的水平位移相同,设为 ,速度的反向延长线均过水平位移的中点,相交于同一点,设两球下落的高度分别为 、 ,则 , ,解得 正确.
8.【答案】D
【详解】根据逆向思维,假设篮球从篮筐中做斜抛运动回到手中,由题分析, 回到手中时,水平距离要远,由抛出的速度方向相同可知, 水平方向速度比 水平方向速度大,在最高点只有水平速度,即 在最高点的速度比 在最高点的速度大,C错误;由速度的分解可知, 抛出的速度比 抛出的速度大,则 起抛时竖直方向的速度比 的大,上升到的最高点比 高,B错误; 上升的时间比 长,且两球从最高点落到相同高度的手中时,根据竖直方向做自由落体运动可知, 下落的时间比 长,所以 比 晚落入篮筐,A错误;在 、 球斜抛轨迹上作篮筐位置的等高线,在实际抛出篮球上升过程中,根据斜抛运动的对称性, 、 两位置处的速度方向相同,D正确.
【关键点拨】解答本题的关键是将斜抛运动的上升过程看作逆向的平抛运动,利用平抛运动规律分析判断.
9.【答案】BC
【详解】根据题意可知,球被抛出后实际上是参与了三个运动,一是沿人骑车的方向上的匀速的直线运动,速度等于人骑车的速度,二是在垂直于人骑车的方向上做速度为的匀速直线运动,三是在竖直方向上做自由落体运动,由可知,由于抛出点等高,运动时间相等
AB.乙骑车速度变大,要想将球投入筐中,应在到达点之前将球抛出,故A错误,B正确;
CD.骑车速度的大小不影响垂直于该方向上的运动,因地面上的塑料筐距骑车路线的垂直距离不变,则抛出速度不变,故D错误,C正确。
故选BC。
10.【答案】AC
【详解】三个物体上升的最大高度相同,则三个物体在空中运动的时间相同,B错误;由对称性知,物体上升时间与下落时间相同,由 知,三个物体抛出时初速度的竖直分量相等,C正确;由题图知,沿路径1抛出的物体水平位移最大,由 知,沿路径1抛出的物体初速度的水平分量最大,D错误;物体落地时的速率 ,则沿路径1抛出的物体落地的速率最大,A正确.
【方法总结】斜上抛运动的对称性
(1)轨迹对称:轨迹关于过最高点的竖直线对称;(2)速度对称:关于过轨迹最高点的竖直线对称的两点的速度大小相等;(3)时间对称:关于过轨迹最高点的竖直线对称的两段过程,上升时间等于下降时间.
11.【答案】AD
【详解】小球沿 轴方向的分运动为匀速直线运动,沿 轴方向的分运动为匀减速直线运动,当小球速度沿 轴方向的分量为零,即 时,小球速度最小,最小速度为 ,A正确;小球的速度大小 ,速度先减小后增大,B错误;小球运动过程中的加速度 ,小球先沿 轴正方向做匀减速运动,减速时间 ,由对称性可知,小球沿 轴反向加速的时间也为 ,小球再次经过 轴所需的时间为 ,C错误;由于小球做类斜抛运动,其运动轨迹为抛物线,D正确.
12.【答案】 4.0m/s 不能 竖直方向的加速度小于重力加速度
【详解】(1)[1]水平方向做匀速直线运动,x-t图线的斜率表示物体运动的速度,则
(2)[2][3]在竖直方向,v-t图线的斜率表示物体运动的加速度,则
由于竖直方向的加速度小于重力加速度,说明排球运动过程中受到的阻力不能忽略。
13.【答案】 10.0 9.76 31.7 36.8 偏小
【详解】(1)[1]因为斜抛过程在水平方向上是匀速直线运动,因此水平速度为
[2]在竖直方向为匀变速直线运动,加速度为g,因此可得
解得
(2)[3]由图可求B点在竖直方向的速度为
因此从B点在竖直方向上可以再升高的高度为
解得
因此总高度为
[4]根据现在最大高度可求起抛时在竖直方向的初速度为
因此起抛时的初速度为
因此礼花弹竖直发射,能够上升的最大高度为
代入数据联立解得
(3)[5] 如果手机拍摄图像时,镜头不是垂直于礼花弹飞行轨迹平面,而是有一个向上的仰角,使竖直方向图像被压缩,则导致竖直方向的距离偏小,因此根据逐差法算出的重力加速度偏小。
14.【答案】(1) ;(2) ;(3)
【详解】(1)根据题意可知落入篮筐时竖直方向速度大小
解得
设篮球从最高点至落入篮筐的时间为 ,有
又
联立求解得
(2)竖直方向有
因此,篮球在空中运动总时间
(3)竖直方向有
且
解得
15.【答案】(1);(2)
【详解】(1)小石子做斜上抛运动,初速度与水平夹角45°,落点恰为最高点,设斜上抛的竖直高度为,则有
,
联立解得
(2)设斜上抛的水平距离为,则有
,
解得
16.【答案】(1)v1 (2) (3)h
【解析】(1)设发球高度为h1时的落地时间为t1,根据平抛运动有h1=g,x1=v1t1,解得x1=v1.
(2)设发球高度为h2,做一次平抛运动的时间为t2,同理有h2=g,x2=v2t2,由于乒乓球反弹后竖直分速度大小不变,则乒乓球可达到的最大高度与发球高度相等,h2=h,2x2=L,得v2=.
(3)根据抛体运动的特点及反弹的对称性,知反弹点到最高点的水平位移为,则反弹点到越过球网的水平位移为L-L=L,乒乓球在水平方向上做匀速直线运动,所以从越过球网到最高点所用的时间和从反弹点到最高点的时间之比为1∶2.对反弹点到最高点的运动采取逆向思维,根据水平方向上的运动和竖直方向上的运动具有等时性,可知越过球网到最高点竖直方向上的时间和反弹点到最高点的时间之比为1∶2.根据h=gt2,可得越过球网到最高点竖直方向上的位移和反弹点到最高点的位移之比为1∶4,即=,解得h3=h.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
一、单选题(本大题共8小题)
1.如图所示,乒乓球在球台上从O点弹起落在M点后,又弹起落在N点,不考虑乒乓球的旋转和空气阻力,则在上述两个过程中( )
A.运动时间相等
B.在最高点时加速度为零
C.在最高点时速度相等
D.在M点与台面碰撞前后速度大小相等
2.篮球是受大众喜爱的运动项目。如图所示,一同学将一篮球从地面上方 B 点斜向上与水平方向成 θ 角(即抛射角)抛出,刚好垂直击中篮板上 A 点,不计空气阻力.若该同学从抛射点 B 向远离篮板方向水平移动一小段距离,仍使抛出的篮球垂直击中 A 点,则可行的是( )
A.增大抛射角θ,同时减小抛出速度 v0
B.减小抛射角θ,同时增大抛射速度v0
C.增大抛射角θ,同时增大抛出速度v0
D.减小抛射角θ,同时减小抛射速度 v0
3.电视综艺节目《加油!向未来》中有一个橄榄球空中击剑游戏:宝剑从空中B点自由下落,同时橄榄球从A点以速度v0沿AB方向抛出,恰好在空中C点沿水平方向击中剑尖,不计空气阻力.关于橄榄球,下列说法正确的是 ( )
A.在空中运动的加速度大于宝剑下落的加速度
B.若以大于v0的速度沿原方向抛出,一定能在C点上方击中剑尖
C.若以小于v0的速度沿原方向抛出,一定能在C点下方击中剑尖
D.无论以多大速度沿原方向抛出,都能击中剑尖
4.如图所示, 、 两篮球从相同高度同时抛出后直接落入篮筐,落入篮筐时的速度方向相同,下列判断正确的是( )
A. 比 先落入篮筐
B. 、 运动的最大高度相同
C. 在最高点的速度比 在最高点的速度小
D. 、 上升到某一相同高度时的速度方向相同
5.如图所示,“跳一跳”游戏需要操作者控制棋子离开平台时的速度,使其能跳到旁边等高平台上.棋子在某次跳跃过程中的轨迹为抛物线,经最高点时速度为 ,此时离平台的高度为 .棋子质量为 ,空气阻力不计,重力加速度为 .则此跳跃过程( )
A.所用时间 B.水平位移大小
C.初速度的竖直分量大小为 D.初速度大小为
6.东京奥林匹克女子标枪决赛,中国田径队在奥运会上迎来了重大突破,刘诗颖以66.34米的个人赛季最好成绩成功夺冠,如图所示.假设3次投掷,标枪的出手位置和离开手时的速度大小相等、方向略有不同.如标枪在空中仅受重力作用且可看成质点.下列说法正确的是 ( )
A.三次投掷,标枪的水平位移都相等
B.三次投掷,标枪的运动时间都相等
C.如忽略刘诗颖投掷标枪时出手点离地高度,当投掷方向与水平方向等于37度角时水平位移最大
D.如忽略刘诗颖投掷标枪时出手点离地高度,当投掷方向与水平方向等于45度角时水平位移最大
7.一学生用两个颜色不同的篮球做斜抛运动游戏,如图所示,第一次出手,红色篮球的初速度与竖直方向的夹角 ;第二次出手,橙色篮球的初速度与竖直方向的夹角 .两次出手的位置在同一竖直线上,结果两篮球正好到达相同的最高点 ,则红色篮球、橙色篮球运动的高度之比为( )
A. B. C. D.
8.如图所示, 、 两篮球从相同高度同时抛出后直接落入篮筐,落入篮筐时的速度方向相同,下列判断正确的是( )
A. 比 先落入篮筐
B. 、 运动的最大高度相同
C. 在最高点的速度比 在最高点的速度小
D. 、 上升到某一相同高度时的速度方向相同
二、多选题(本大题共3小题)
9.在某次骑车投球,比赛中,甲、乙两参赛者在沿规定直轨道匀速骑行过程中,将手中网球沿垂直于骑行方向水平抛向地面上的塑料筐中,如图,点是轨道上离框最近的点。甲以的速度骑行,在点将网球以相对于人的速度水平抛出,网球恰好落人筐中;乙以的速度骑行,在与甲的抛出点等高处将球水平抛出,要想将球投入筐中,乙参赛者应( )(不计空气阻力)
A.在到达点之后将球抛出
B.在到达点之前将球抛出
C.将球也以速度水平抛出
D.将球以大于的速度水平抛出
10.(多选)如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
A.沿路径1抛出的物体落地的速率最大
B.沿路径3抛出的物体在空中运动的时间最长
C.三个物体抛出时初速度的竖直分量相等
D.三个物体抛出时初速度的水平分量相等
11.(多选)如图所示,一个质量 的小球在光滑水平面上运动, 时刻小球经过坐标原点 ,速度方向与 轴正方向的夹角为 ,速度大小 ,此刻开始对小球施加一个沿 轴负方向的水平恒力 ,已知 .下列判断正确的是( )
A.此后小球运动的最小速度为 B.此后小球的速度先增大后减小
C.小球再次经过 轴所需的时间为 D.小球的运动轨迹应为抛物线
三、实验题(本大题共2小题)
12.某物理兴趣小组借助视频分析软件来研究排球的运动。他们先从正面拍摄了一段排球运动的视频,在画面中建立直角坐标系,并选定排球网柱作为比例尺,这样画面中所有对象的位置信息就可以被定量记录下来,接着,在分析软件中将拍摄好的视频按照设定的时间间隔逐帧播放,那么每帧画面所对应的时间信息也就确定下来了,基于此,他们得到了排球运动的相关图像,如图所示。已知当地的重力加速速度为g=9.8m/s2。
(1)由图2(a)可知,排球水平方向的运动可以近似看作匀速直线运动,其水平速度为: 。(结果保留两位有效数字)
(2)由图2(b)可知,排球运动过程中受到的空气阻力 (填“能”或者“不能”)忽略不计,原因是 。
13.节日放出的礼花弹炫丽夺目,往往能将当夜的活动推到高潮。某同学将手机镜头垂直于礼花弹飞行轨迹平面,使用摄像功能研究礼花弹的运动。礼花弹从发射筒射出后,手机拍摄到了一颗礼花弹发射后在空中自由飞行的部分轨迹,经手机APP处理(找出竖直对称轴)并测出了几个位置的坐标数据,如图所示。其中,点为发射筒出口,A、B、C是从拍摄图像中选择的时间间隔为的三个位置。由此可以确定(注意:计算结果均保留3位有效数字)
(1)该礼花弹飞行的水平分速度为 ,当地重力加速度为
(2)该礼花弹飞行的最大高度为 ,如果礼花弹竖直发射,能够上升的最大高度为 ;
(3)如果手机拍摄图像时,镜头不是垂直于礼花弹飞行轨迹平面,而是有一个向上的仰角,使竖直方向图像被压缩,则测量得到的重力加速度将 (选填“偏大”、“偏小”、“不变”)。
四、解答题(本大题共3小题)
14.在篮球比赛中,篮球投出时角度太大或太小,都会影响投篮的命中率。在某次投篮时,篮球以与水平面成 的倾角准确落入篮筐,若投球点和篮筐正好在同一水平面上(如图所示),投球点到篮筐距离为 ,不考虑空气阻力,重力加速度 取 。求:
(1)篮球运动至最高点时速度 的大小;
(2)篮球在空中运动的时间t;
(3)篮球运动中的最高位置相对篮筐的竖直高度 。
15.[山东潍坊诸城、安丘、高密2023高一下期中](15分)水平地面上有一足够长的固定斜面,倾角为37°,小华站在斜面底端向斜面上投郑小石子。若小石子出手时的初速度方向与水平方向成45°,出手高度为站立点正上方处,小石子的飞行轨迹所在平面与斜面底边垂直,落在斜面上时速度方向恰好水平。已知站立点到落点的距离为,重力加速度,,,不计空气阻力。求:
(1)小石子在空中的飞行时间;
(2)小石子出手时初速度的大小。
16.(16分)抛体运动在各类体育运动项目中都很常见,如乒乓球运动.现讨论乒乓球发球问题,设球台长2L、网高h,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,如图所示.不考虑乒乓球的旋转和空气阻力(设重力加速度为g).
(1)若球在球台边缘O点正上方高度为h1处以速度v1水平发出,落在球台上的P1点(运动轨迹如图中实线所示),求P1点距O点的距离x1.
(2)若球在O点正上方以速度v2水平发出,经反弹恰好在最高点时越过球网落在球台上的P2点(运动轨迹如图中虚线所示),求v2的大小.
(3)若球在O点正上方水平发出后,经反弹恰好越过球网且刚好落在对方球台边缘P3处,求发球点距O点的高度h3.
参考答案
1.【答案】A
【详解】A.两次的高度相同,且每次从最高点到落在球台上做平抛运动,由公式可知,做平抛运动的时间相同,根据对称性可知,两次运动时间相等,故A正确;
B.在最高点时球还受到重力的作用,则加速度为重力加速度,故B错误;
C.由于运动时间相等,两次水平方向的位移不同,则水平方向的初速度不相同,说明在最高点时速度不相等,故C错误;
D.由于高度相等,由公式可知,在M点与台面碰撞前后竖直方向的速度大小相等,且初速度大小不同,由平行四边形定则可知,在M点与台面碰撞前后速度大小不相等,故D错误。
故选A。
2.【答案】B
【详解】由于篮球垂直击中A点,其逆过程是平抛运动,抛射点B向远离篮板方向水平移动一小段距离,由于平抛运动的高度不变,运动时间不变,水平位移变大,初速度变大。落地时水平速度变大,竖直速度不变,则落地速度方向与水平面的夹角变小。因此只有减小抛射角,同时增大抛出速度,才能仍垂直打到篮板上。故B正确,ACD错误。
故选B。
3.【答案】B
【解析】橄榄球在空中做斜抛运动,其在空中运动的加速度等于宝剑下落的加速度,选项A错误;当橄榄球的初速度大于v0时,水平方向分速度增加,而水平方向位移不变,所以时间减小,宝剑从B点下落的距离减小,橄榄球肯定在C点上方击中剑尖,选项B正确;如果橄榄球的初速度小于v0,宝剑落地时橄榄球水平方向位移可能小于A点到BC的水平距离,此时不能击中剑尖,选项C、D错误.
4.【答案】D
【详解】根据逆向思维,假设篮球从篮筐中做斜抛运动回到手中,由题分析, 回到手中时,水平距离要远,由抛出的速度方向相同可知, 水平方向速度比 水平方向速度大,在最高点只有水平速度,即 在最高点的速度比 在最高点的速度大,C错误;由速度的分解可知, 抛出的速度比 抛出的速度大,则 起抛时竖直方向的速度比 的大,上升到的最高点比 高,B错误; 上升的时间比 长,且两球从最高点落到相同高度的手中时,根据竖直方向做自由落体运动可知, 下落的时间比 长,所以 比 晚落入篮筐,A错误;在 、 球斜抛轨迹上作篮筐位置的等高线,在实际抛出篮球上升过程中,根据斜抛运动的对称性, 、 两位置处的速度方向相同,D正确.
【关键点拨】解答本题的关键是将斜抛运动的上升过程看作逆向的平抛运动,利用平抛运动规律分析判断.
5.【答案】B
【详解】竖直方向,由 ,可得 ,该斜抛运动等效为两个完全相同的平抛运动,时间是 ,A错误;水平位移 ,B正确;初速度的竖直分量大小 ,C错误;初速度大小 ,D错误.
6.【答案】D
【解析】设标枪离开手时的速度方向与水平方向夹角θ,则竖直方向有vy=vsin θ,设标枪的出手位置距离地面的高度为h,取向上为正方向,则运动的时间-h=vyt-gt2=(vsin θ)t-gt2,解得t=(另一个不符合题意舍掉),角度不同,时间不相等,水平位移x=(vcos θ)t可知水平位移不一定相等,A、B错误;根据竖直方向vy=vsin θ,则运动的时间t=2=,水平位移x=(vcos θ)t解得x=,知θ=45°时,sin2θ最大,则落地点和抛出点间的水平距离最大,C错误,D正确.
7.【答案】A
【详解】两个不同颜色的篮球做斜抛运动,到达相同的最高点,可将其逆运动看成水平向左的平抛运动,运动轨迹如图所示,两平抛运动的水平位移相同,设为 ,速度的反向延长线均过水平位移的中点,相交于同一点,设两球下落的高度分别为 、 ,则 , ,解得 正确.
8.【答案】D
【详解】根据逆向思维,假设篮球从篮筐中做斜抛运动回到手中,由题分析, 回到手中时,水平距离要远,由抛出的速度方向相同可知, 水平方向速度比 水平方向速度大,在最高点只有水平速度,即 在最高点的速度比 在最高点的速度大,C错误;由速度的分解可知, 抛出的速度比 抛出的速度大,则 起抛时竖直方向的速度比 的大,上升到的最高点比 高,B错误; 上升的时间比 长,且两球从最高点落到相同高度的手中时,根据竖直方向做自由落体运动可知, 下落的时间比 长,所以 比 晚落入篮筐,A错误;在 、 球斜抛轨迹上作篮筐位置的等高线,在实际抛出篮球上升过程中,根据斜抛运动的对称性, 、 两位置处的速度方向相同,D正确.
【关键点拨】解答本题的关键是将斜抛运动的上升过程看作逆向的平抛运动,利用平抛运动规律分析判断.
9.【答案】BC
【详解】根据题意可知,球被抛出后实际上是参与了三个运动,一是沿人骑车的方向上的匀速的直线运动,速度等于人骑车的速度,二是在垂直于人骑车的方向上做速度为的匀速直线运动,三是在竖直方向上做自由落体运动,由可知,由于抛出点等高,运动时间相等
AB.乙骑车速度变大,要想将球投入筐中,应在到达点之前将球抛出,故A错误,B正确;
CD.骑车速度的大小不影响垂直于该方向上的运动,因地面上的塑料筐距骑车路线的垂直距离不变,则抛出速度不变,故D错误,C正确。
故选BC。
10.【答案】AC
【详解】三个物体上升的最大高度相同,则三个物体在空中运动的时间相同,B错误;由对称性知,物体上升时间与下落时间相同,由 知,三个物体抛出时初速度的竖直分量相等,C正确;由题图知,沿路径1抛出的物体水平位移最大,由 知,沿路径1抛出的物体初速度的水平分量最大,D错误;物体落地时的速率 ,则沿路径1抛出的物体落地的速率最大,A正确.
【方法总结】斜上抛运动的对称性
(1)轨迹对称:轨迹关于过最高点的竖直线对称;(2)速度对称:关于过轨迹最高点的竖直线对称的两点的速度大小相等;(3)时间对称:关于过轨迹最高点的竖直线对称的两段过程,上升时间等于下降时间.
11.【答案】AD
【详解】小球沿 轴方向的分运动为匀速直线运动,沿 轴方向的分运动为匀减速直线运动,当小球速度沿 轴方向的分量为零,即 时,小球速度最小,最小速度为 ,A正确;小球的速度大小 ,速度先减小后增大,B错误;小球运动过程中的加速度 ,小球先沿 轴正方向做匀减速运动,减速时间 ,由对称性可知,小球沿 轴反向加速的时间也为 ,小球再次经过 轴所需的时间为 ,C错误;由于小球做类斜抛运动,其运动轨迹为抛物线,D正确.
12.【答案】 4.0m/s 不能 竖直方向的加速度小于重力加速度
【详解】(1)[1]水平方向做匀速直线运动,x-t图线的斜率表示物体运动的速度,则
(2)[2][3]在竖直方向,v-t图线的斜率表示物体运动的加速度,则
由于竖直方向的加速度小于重力加速度,说明排球运动过程中受到的阻力不能忽略。
13.【答案】 10.0 9.76 31.7 36.8 偏小
【详解】(1)[1]因为斜抛过程在水平方向上是匀速直线运动,因此水平速度为
[2]在竖直方向为匀变速直线运动,加速度为g,因此可得
解得
(2)[3]由图可求B点在竖直方向的速度为
因此从B点在竖直方向上可以再升高的高度为
解得
因此总高度为
[4]根据现在最大高度可求起抛时在竖直方向的初速度为
因此起抛时的初速度为
因此礼花弹竖直发射,能够上升的最大高度为
代入数据联立解得
(3)[5] 如果手机拍摄图像时,镜头不是垂直于礼花弹飞行轨迹平面,而是有一个向上的仰角,使竖直方向图像被压缩,则导致竖直方向的距离偏小,因此根据逐差法算出的重力加速度偏小。
14.【答案】(1) ;(2) ;(3)
【详解】(1)根据题意可知落入篮筐时竖直方向速度大小
解得
设篮球从最高点至落入篮筐的时间为 ,有
又
联立求解得
(2)竖直方向有
因此,篮球在空中运动总时间
(3)竖直方向有
且
解得
15.【答案】(1);(2)
【详解】(1)小石子做斜上抛运动,初速度与水平夹角45°,落点恰为最高点,设斜上抛的竖直高度为,则有
,
联立解得
(2)设斜上抛的水平距离为,则有
,
解得
16.【答案】(1)v1 (2) (3)h
【解析】(1)设发球高度为h1时的落地时间为t1,根据平抛运动有h1=g,x1=v1t1,解得x1=v1.
(2)设发球高度为h2,做一次平抛运动的时间为t2,同理有h2=g,x2=v2t2,由于乒乓球反弹后竖直分速度大小不变,则乒乓球可达到的最大高度与发球高度相等,h2=h,2x2=L,得v2=.
(3)根据抛体运动的特点及反弹的对称性,知反弹点到最高点的水平位移为,则反弹点到越过球网的水平位移为L-L=L,乒乓球在水平方向上做匀速直线运动,所以从越过球网到最高点所用的时间和从反弹点到最高点的时间之比为1∶2.对反弹点到最高点的运动采取逆向思维,根据水平方向上的运动和竖直方向上的运动具有等时性,可知越过球网到最高点竖直方向上的时间和反弹点到最高点的时间之比为1∶2.根据h=gt2,可得越过球网到最高点竖直方向上的位移和反弹点到最高点的位移之比为1∶4,即=,解得h3=h.
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
同课章节目录
