高考物理一轮复习 生活中的圆周运动分类专题1:共轴传动、皮带传动及齿轮传动问题(含解析)
文档属性
| 名称 | 高考物理一轮复习 生活中的圆周运动分类专题1:共轴传动、皮带传动及齿轮传动问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 700.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-31 18:37:34 | ||
图片预览



文档简介
共轴传动、皮带传动及齿轮传动问题
一、单选题(本大题共8小题)
1.在G20峰会“最忆是杭州”的文化文艺演出中,芭蕾舞演员保持如图所示姿势原地旋转,此时手臂上A、B两点角速度大小分别为、,线速度大小分别为、,则( )
A. B. C. D.
2.如图所示,用起瓶器打开瓶盖,起瓶器上A、B两点绕O点转动的角速度分别为ωA和ωB,线速度大小分别为vA和vB,则( )
A.ωA=ωB,vA>vB B.ωA=ωB,vAC.ωA<ωB,vA=vB D.ωA>ωB,vA=vB
3.[山西长治二中2022高一下月考]如图所示, 和 是一组塔轮,即 和 半径不同,但固定在同一转动轴上,其半径之比为 轮的半径与 轮相同,它与 轮紧靠在一起.当 轮绕其中心的竖直轴转动时,由于摩擦作用, 轮也会随之无滑动地转动. 、 、 分别为三个转轮 、 、 边缘上的三个点,在运动过程中, 、 、 三点的( )
A.线速度大小之比为 B.角速度大小之比为
C.转速之比为 D.向心加速度大小之比为
4.如图所示,甲,乙两人分别站在赤道和纬度为45°的地面上,他们随地球一起绕地轴做匀速圆周运动,下列物理量相同的是( )
A.向心力 B.角速度 C.线速度 D.向心加速度
5.[山东泰安2022高一下期中]如图所示,自行车的大齿轮与小齿轮通过链条相连,而后轮与小齿轮是绕共同的轴转动的.设大齿轮、小齿轮和后轮的半径分别为 、 和 ,其半径之比为 ,在它们的边缘分别取一点 、 、 .在运动过程中, 、 、 三点的( )
A.线速度大小之比为 B.角速度之比为
C.转速之比为 D.向心加速度大小之比为
6.如图所示,一个大轮通过皮带拉着小轮转动,皮带和两轮之间无相对滑动,大轮的半径是小轮半径的2倍,大轮上的一点S离转动轴的距离是大轮半径的.P、Q分别为两轮边缘上的点,则P、Q、S三点的 ( )
A.线速度大小之比为1∶1∶3
B.角速度大小之比为1∶3∶1
C.转动周期之比为2∶1∶1
D.向心加速度大小之比为3∶6∶1
7.如图所示,半径分别为R和的两个转盘A、B处于水平面内,两者边缘紧密接触,靠静摩擦传动,均可以绕竖直方向的转轴及转动.一个小滑块(视为质点)位于转盘A的边缘,已知滑块与转盘间的动摩擦因数为,重力加速度大小为g,滑动摩擦力等于最大静摩擦力.现使转盘B的转速逐渐增大,当小滑块恰好要相对于转盘A发生相对运动时,转盘B的角速度大小为( )
A. B. C. D.
8.如图,大、小两轮通过皮带传动匀速转动,且皮带与轮边缘之间不发生相对滑动。大、小两轮的半径之比r1:r2=2:1,A、B为轮边缘上的两点。下列关系正确的是( )
A.A、B两点的线速度大小之比vA:vB=1:1
B.A、B两点的线速度大小之比vA:vB=2:1
C.A、B两点的角速度大小之比ωA: ωB=1:1
D.A、B两点的向心加速度大小之比aA: aB=2:1
二、多选题(本大题共3小题)
9.(多选)如图甲为某小区出入口采用的栅栏道闸.如图乙所示, 为栅栏道闸的转动杆, 为竖直杆. 为两杆的交点, 为竖杆上的点.在道闸抬起过程中,杆 始终保持竖直,在杆 绕 点从与水平方向成 匀速转动到 的过程中( )
甲
乙
A. 点的线速度等于 点的线速度
B. 点的角速度大于 点的角速度
C. 点的向心加速度大于 点的向心加速度
D. 、 两点的路程相同
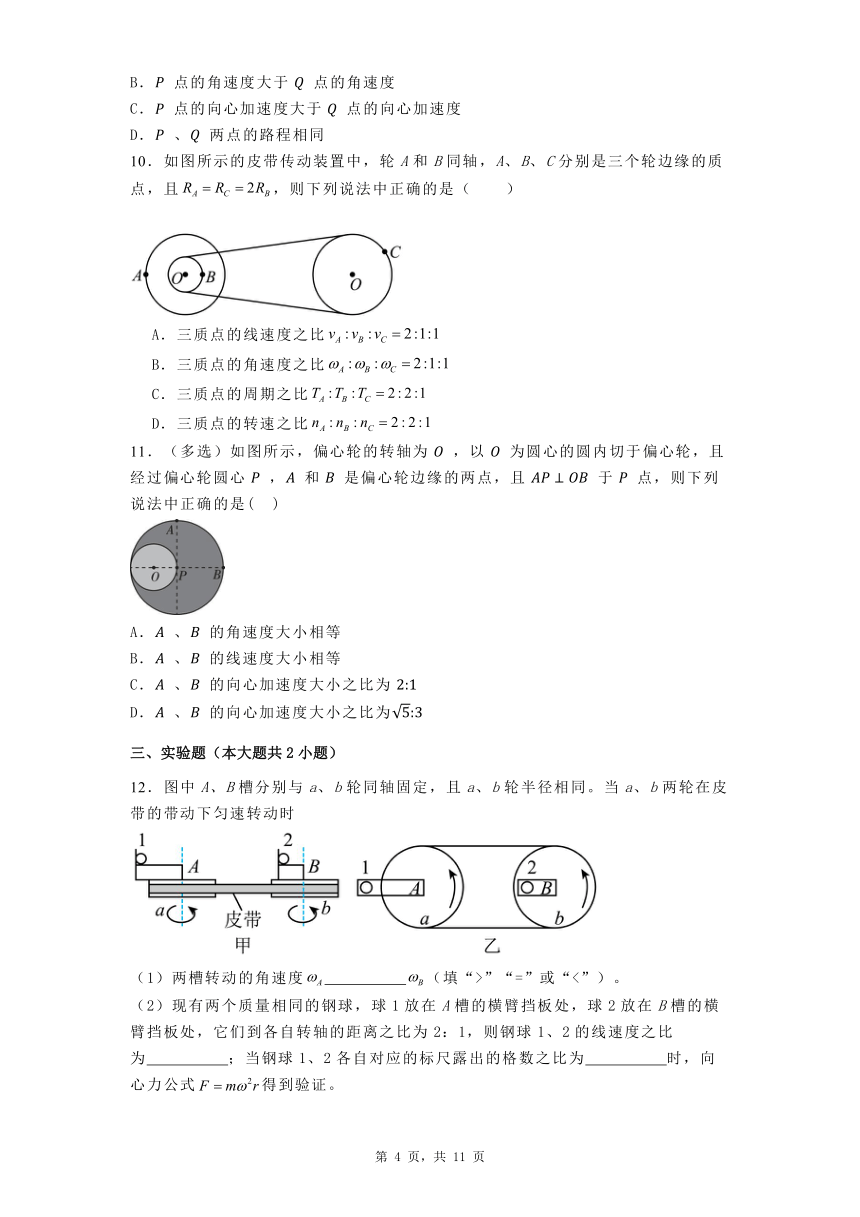
10.如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且,则下列说法中正确的是( )
A.三质点的线速度之比
B.三质点的角速度之比
C.三质点的周期之比
D.三质点的转速之比
11.(多选)如图所示,偏心轮的转轴为 ,以 为圆心的圆内切于偏心轮,且经过偏心轮圆心 , 和 是偏心轮边缘的两点,且 于 点,则下列说法中正确的是( )
A. 、 的角速度大小相等
B. 、 的线速度大小相等
C. 、 的向心加速度大小之比为
D. 、 的向心加速度大小之比为
三、实验题(本大题共2小题)
12.图中A、B槽分别与a、b轮同轴固定,且a、b轮半径相同。当a、b两轮在皮带的带动下匀速转动时
(1)两槽转动的角速度 (填“>”“=”或“<”)。
(2)现有两个质量相同的钢球,球1放在A槽的横臂挡板处,球2放在B槽的横臂挡板处,它们到各自转轴的距离之比为2:1,则钢球1、2的线速度之比为 ;当钢球1、2各自对应的标尺露出的格数之比为 时,向心力公式得到验证。
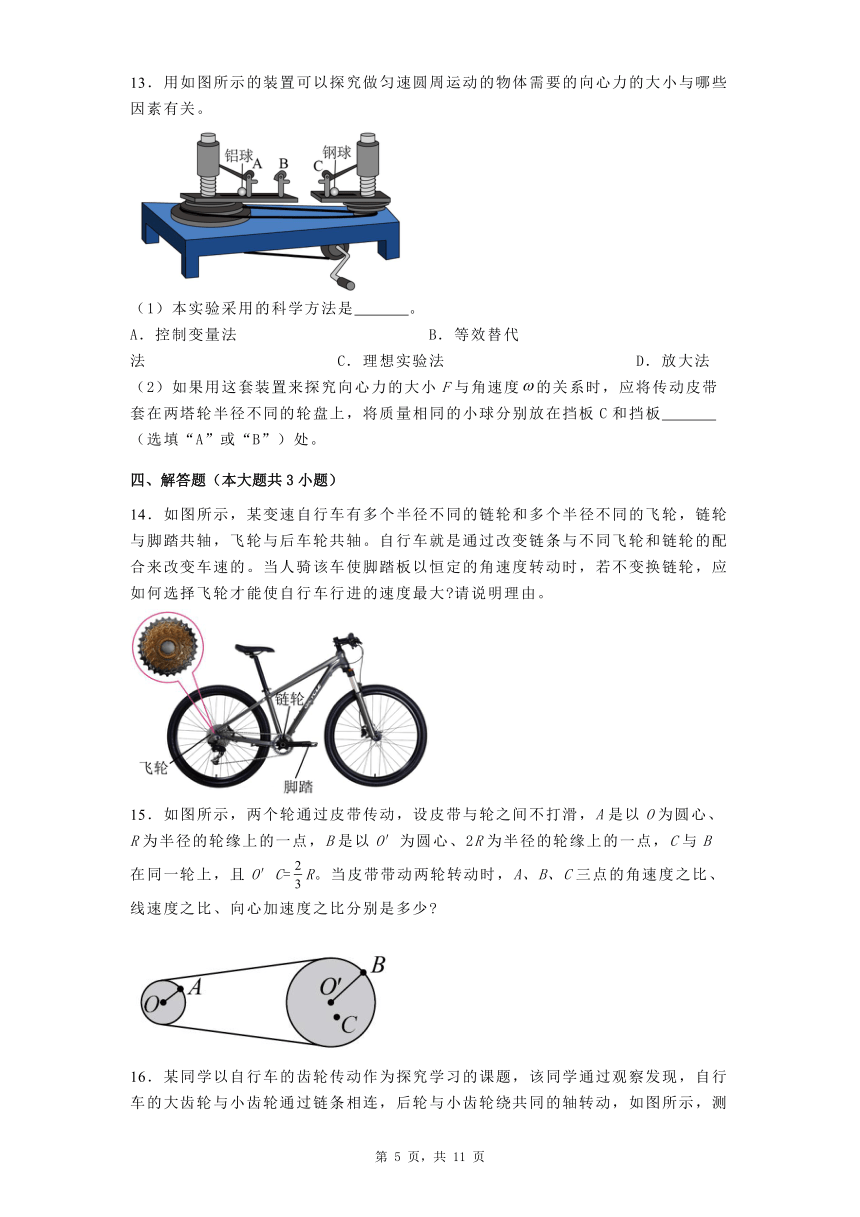
13.用如图所示的装置可以探究做匀速圆周运动的物体需要的向心力的大小与哪些因素有关。
(1)本实验采用的科学方法是 。
A.控制变量法 B.等效替代法 C.理想实验法 D.放大法
(2)如果用这套装置来探究向心力的大小F与角速度的关系时,应将传动皮带套在两塔轮半径不同的轮盘上,将质量相同的小球分别放在挡板C和挡板 (选填“A”或“B”)处。
四、解答题(本大题共3小题)
14.如图所示,某变速自行车有多个半径不同的链轮和多个半径不同的飞轮,链轮与脚踏共轴,飞轮与后车轮共轴。自行车就是通过改变链条与不同飞轮和链轮的配合来改变车速的。当人骑该车使脚踏板以恒定的角速度转动时,若不变换链轮,应如何选择飞轮才能使自行车行进的速度最大 请说明理由。
15.如图所示,两个轮通过皮带传动,设皮带与轮之间不打滑,A是以O为圆心、R为半径的轮缘上的一点,B是以O′为圆心、2R为半径的轮缘上的一点,C与B在同一轮上,且O′C=R。当皮带带动两轮转动时,A、B、C三点的角速度之比、线速度之比、向心加速度之比分别是多少
16.某同学以自行车的齿轮传动作为探究学习的课题,该同学通过观察发现,自行车的大齿轮与小齿轮通过链条相连,后轮与小齿轮绕共同的轴转动,如图所示,测得大齿轮的半径为r1、小齿轮的半径为r2、自行车后轮的半径为R,若测得在时间t内大齿轮转动的圈数为N,求:
(1)大齿轮转动角速度的大小ω;
(2)自行车后轮线速度的大小v。
共轴传动、皮带传动及齿轮传动问题参考答案
1.【答案】D
【详解】可以把A、B两点看成是同轴转动的两个质点,则,由得,故D选项正确.
故选D
点睛:同轴角速度相等,同皮带线速度相等,然后借助于 求解.
2.【答案】B
【详解】同轴转动,角速度相等,,由于,根据,,选B。
3.【答案】D
【详解】 轮、 轮靠摩擦转动,则两轮边缘点的线速度大小相等,故 ,根据 ,可得 ,根据 ,可得 ,根据 ,可得 ; 轮、 轮共轴转动,角速度相等,故 ,根据 ,可得 ,根据 ,可得 ,根据 ,可得 .综合得到 , , , ,故选D.
4.【答案】B
【详解】
AB.甲乙两人站在地球上都绕地轴转动,角速度相等,根据向心力公式
可知,半径不等,向心力不等,故A错误,B正确。
C.根据线速度与角速度关系
可知,半径不等,则线速度不等,故C错误。
D.根据向心加速度公式
可知,半径不等,则向心加速度不等,故D错误。
故选B。
5.【答案】D
【详解】大齿轮和小齿轮通过链条传动,则 、 两点线速度相等,小齿轮和后轮为同轴转动,则 、 两点角速度相同,则有 ,故A、 、 三点的线速度大小之比为 ,A错误; 、 两点线速度相等,则角速度之比为 ,故A、 、 三点的角速度之比为 ,B错误;由于 、 两点角速度之比为 ,由 得, 、 两点转速之比为 , 、 两点转速相同,则 、 、 三点的转速之比为 ,C错误;由 可知, 、 两点的向心加速度之比为 ,由 可知, 、 两点的向心加速度之比为 ,所以 、 、 三点的向心加速度之比为 ,D正确.
6.【答案】D
【解析】设大轮半径为r1,小轮半径为r2,P、Q两点由皮带传动,所以=,P、S两点同轴转动,则ωP=ωS,根据线速度与角速度关系v=ωr,可知P、S两点的线速度关系为==,所以三点的线速度大小之比为3∶3∶1,选项A错误;P、Q两点角速度大小关系=·=,所以三点的角速度大小之比为1∶2∶1,选项B错误;根据ω=可知三点的周期之比为2∶1∶2,选项C错误;根据an=ω2r可知P、S两点的向心加速度大小之比=·=,根据an=可知P、Q两点的向心加速度大小之比=·=,所以三点的向心加速度大小之比为3∶6∶1,选项D正确.
7.【答案】A
【详解】
对小滑块向心力等于最大静摩擦力
μmg=mRω2
所以小圆盘转动的角速度为
A点的线速度为
所以B点的线速度大小为
则B点的角速度为
.
BCD错误,A正确。
故选A。
8.【答案】A
【详解】
AB.A、B两点是同缘转动,则线速度相等,即线速度大小之比
vA:vB=1:1
选项A正确,B错误;
C.根据
可知,A、B两点的角速度大小之比
ωA: ωB=1:2
选项C错误;
D.根据
可知,A、B两点的向心加速度大小之比
aA: aB=1:2
选项D错误。
故选A。
9.【答案】AD
【详解】由于 、 两点在同一竖直杆上,而且杆运动时始终保持竖直,所以在杆 绕 点从与水平方向成 匀速转动到 的过程中,两点都做半径相同的匀速圆周运动,故两点的线速度、角速度都相等,A正确,B错误;根据向心加速度等于角速度与线速度的乘积可知, 、 两点的向心加速度也相等,C错误;线速度相等,运动时间相等,则 、 两点的路程相等,D正确.
10.【答案】AD
【详解】质点A、B同轴,二者具有相同的角速度、周期和转速,即,,。并且有
质点B、C分通过皮带传动,二者具有相同的线速度,即,则有
A.根据以上分析可知,,故A正确。
B.根据以上分析可知,,故B错误。
C.根据以上分析可知,,故C错误
D.根据以上分析可知,,故D正确。
故选AD。
11.【答案】AD
【详解】 、 两点同轴转动,角速度大小相等,故A正确;由几何关系可知 、 的转动半径之比为 ,由线速度 可知 、 的线速度大小不相等,故B错误;根据向心加速度 可得, 、 的向心加速度大小之比为 ,故C错误,D正确.
12.【答案】 = 2:1 2:1
【详解】(1)[1]由于a、b轮半径相同,通过皮带传动线速度大小相同,故两槽转动的角速度满足
(2)[2]现有两个质量相同的钢球,球1放在A槽的横臂挡板处,球2放在B槽的横臂挡板处,它们到各自转轴的距离之比为2:1,由可知,钢球1、2的线速度之比为2:1。
[3]由向心力表达式可知,两钢球质量相同、转动角速度相同,则向心力大小与轨道半径成正比,故钢球1、2各自对应的标尺露出的格数之比为2:1。
13.【答案】 A A
【详解】(1)[1]本装置的原理是使物体质量、半径、角速度三个物理量其中的一个变化,控制其他物理量不变,从而研究向心力与各物理量之间的关系,故采用的是控制变量法;
(2)[2]根据可知,控制质量相同和半径相同,所以将质量相同的小球分别放在挡板C和挡板A处。
14.【答案】见解析
【详解】当人骑该车使脚踏板以恒定的角速度转动时,若不变换链轮,则飞轮边缘线速度不变;根据 可知,选择半径最小的飞轮,飞轮角速度最大,则后轮角速度最大,而后轮半径不变,则自行车行进的速度最大。
15.【答案】;
【详解】
B、C两点随同一个轮转动,角速度相等,A、B两点通过皮带传动,线速度大小相等,由
可得
可得
由
得
由
可得
则
16.【答案】(1);(2)
【详解】
(1)大齿轮的周期
则
大齿轮转动角速度的大小
(2)大齿轮和小齿轮边缘线速度的大小相等,有
解得小齿轮角速度的大小
小齿轮角速度与后轮角速度的大小相等,则后轮线速度的大小
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
一、单选题(本大题共8小题)
1.在G20峰会“最忆是杭州”的文化文艺演出中,芭蕾舞演员保持如图所示姿势原地旋转,此时手臂上A、B两点角速度大小分别为、,线速度大小分别为、,则( )
A. B. C. D.
2.如图所示,用起瓶器打开瓶盖,起瓶器上A、B两点绕O点转动的角速度分别为ωA和ωB,线速度大小分别为vA和vB,则( )
A.ωA=ωB,vA>vB B.ωA=ωB,vA
3.[山西长治二中2022高一下月考]如图所示, 和 是一组塔轮,即 和 半径不同,但固定在同一转动轴上,其半径之比为 轮的半径与 轮相同,它与 轮紧靠在一起.当 轮绕其中心的竖直轴转动时,由于摩擦作用, 轮也会随之无滑动地转动. 、 、 分别为三个转轮 、 、 边缘上的三个点,在运动过程中, 、 、 三点的( )
A.线速度大小之比为 B.角速度大小之比为
C.转速之比为 D.向心加速度大小之比为
4.如图所示,甲,乙两人分别站在赤道和纬度为45°的地面上,他们随地球一起绕地轴做匀速圆周运动,下列物理量相同的是( )
A.向心力 B.角速度 C.线速度 D.向心加速度
5.[山东泰安2022高一下期中]如图所示,自行车的大齿轮与小齿轮通过链条相连,而后轮与小齿轮是绕共同的轴转动的.设大齿轮、小齿轮和后轮的半径分别为 、 和 ,其半径之比为 ,在它们的边缘分别取一点 、 、 .在运动过程中, 、 、 三点的( )
A.线速度大小之比为 B.角速度之比为
C.转速之比为 D.向心加速度大小之比为
6.如图所示,一个大轮通过皮带拉着小轮转动,皮带和两轮之间无相对滑动,大轮的半径是小轮半径的2倍,大轮上的一点S离转动轴的距离是大轮半径的.P、Q分别为两轮边缘上的点,则P、Q、S三点的 ( )
A.线速度大小之比为1∶1∶3
B.角速度大小之比为1∶3∶1
C.转动周期之比为2∶1∶1
D.向心加速度大小之比为3∶6∶1
7.如图所示,半径分别为R和的两个转盘A、B处于水平面内,两者边缘紧密接触,靠静摩擦传动,均可以绕竖直方向的转轴及转动.一个小滑块(视为质点)位于转盘A的边缘,已知滑块与转盘间的动摩擦因数为,重力加速度大小为g,滑动摩擦力等于最大静摩擦力.现使转盘B的转速逐渐增大,当小滑块恰好要相对于转盘A发生相对运动时,转盘B的角速度大小为( )
A. B. C. D.
8.如图,大、小两轮通过皮带传动匀速转动,且皮带与轮边缘之间不发生相对滑动。大、小两轮的半径之比r1:r2=2:1,A、B为轮边缘上的两点。下列关系正确的是( )
A.A、B两点的线速度大小之比vA:vB=1:1
B.A、B两点的线速度大小之比vA:vB=2:1
C.A、B两点的角速度大小之比ωA: ωB=1:1
D.A、B两点的向心加速度大小之比aA: aB=2:1
二、多选题(本大题共3小题)
9.(多选)如图甲为某小区出入口采用的栅栏道闸.如图乙所示, 为栅栏道闸的转动杆, 为竖直杆. 为两杆的交点, 为竖杆上的点.在道闸抬起过程中,杆 始终保持竖直,在杆 绕 点从与水平方向成 匀速转动到 的过程中( )
甲
乙
A. 点的线速度等于 点的线速度
B. 点的角速度大于 点的角速度
C. 点的向心加速度大于 点的向心加速度
D. 、 两点的路程相同
10.如图所示的皮带传动装置中,轮A和B同轴,A、B、C分别是三个轮边缘的质点,且,则下列说法中正确的是( )
A.三质点的线速度之比
B.三质点的角速度之比
C.三质点的周期之比
D.三质点的转速之比
11.(多选)如图所示,偏心轮的转轴为 ,以 为圆心的圆内切于偏心轮,且经过偏心轮圆心 , 和 是偏心轮边缘的两点,且 于 点,则下列说法中正确的是( )
A. 、 的角速度大小相等
B. 、 的线速度大小相等
C. 、 的向心加速度大小之比为
D. 、 的向心加速度大小之比为
三、实验题(本大题共2小题)
12.图中A、B槽分别与a、b轮同轴固定,且a、b轮半径相同。当a、b两轮在皮带的带动下匀速转动时
(1)两槽转动的角速度 (填“>”“=”或“<”)。
(2)现有两个质量相同的钢球,球1放在A槽的横臂挡板处,球2放在B槽的横臂挡板处,它们到各自转轴的距离之比为2:1,则钢球1、2的线速度之比为 ;当钢球1、2各自对应的标尺露出的格数之比为 时,向心力公式得到验证。
13.用如图所示的装置可以探究做匀速圆周运动的物体需要的向心力的大小与哪些因素有关。
(1)本实验采用的科学方法是 。
A.控制变量法 B.等效替代法 C.理想实验法 D.放大法
(2)如果用这套装置来探究向心力的大小F与角速度的关系时,应将传动皮带套在两塔轮半径不同的轮盘上,将质量相同的小球分别放在挡板C和挡板 (选填“A”或“B”)处。
四、解答题(本大题共3小题)
14.如图所示,某变速自行车有多个半径不同的链轮和多个半径不同的飞轮,链轮与脚踏共轴,飞轮与后车轮共轴。自行车就是通过改变链条与不同飞轮和链轮的配合来改变车速的。当人骑该车使脚踏板以恒定的角速度转动时,若不变换链轮,应如何选择飞轮才能使自行车行进的速度最大 请说明理由。
15.如图所示,两个轮通过皮带传动,设皮带与轮之间不打滑,A是以O为圆心、R为半径的轮缘上的一点,B是以O′为圆心、2R为半径的轮缘上的一点,C与B在同一轮上,且O′C=R。当皮带带动两轮转动时,A、B、C三点的角速度之比、线速度之比、向心加速度之比分别是多少
16.某同学以自行车的齿轮传动作为探究学习的课题,该同学通过观察发现,自行车的大齿轮与小齿轮通过链条相连,后轮与小齿轮绕共同的轴转动,如图所示,测得大齿轮的半径为r1、小齿轮的半径为r2、自行车后轮的半径为R,若测得在时间t内大齿轮转动的圈数为N,求:
(1)大齿轮转动角速度的大小ω;
(2)自行车后轮线速度的大小v。
共轴传动、皮带传动及齿轮传动问题参考答案
1.【答案】D
【详解】可以把A、B两点看成是同轴转动的两个质点,则,由得,故D选项正确.
故选D
点睛:同轴角速度相等,同皮带线速度相等,然后借助于 求解.
2.【答案】B
【详解】同轴转动,角速度相等,,由于,根据,,选B。
3.【答案】D
【详解】 轮、 轮靠摩擦转动,则两轮边缘点的线速度大小相等,故 ,根据 ,可得 ,根据 ,可得 ,根据 ,可得 ; 轮、 轮共轴转动,角速度相等,故 ,根据 ,可得 ,根据 ,可得 ,根据 ,可得 .综合得到 , , , ,故选D.
4.【答案】B
【详解】
AB.甲乙两人站在地球上都绕地轴转动,角速度相等,根据向心力公式
可知,半径不等,向心力不等,故A错误,B正确。
C.根据线速度与角速度关系
可知,半径不等,则线速度不等,故C错误。
D.根据向心加速度公式
可知,半径不等,则向心加速度不等,故D错误。
故选B。
5.【答案】D
【详解】大齿轮和小齿轮通过链条传动,则 、 两点线速度相等,小齿轮和后轮为同轴转动,则 、 两点角速度相同,则有 ,故A、 、 三点的线速度大小之比为 ,A错误; 、 两点线速度相等,则角速度之比为 ,故A、 、 三点的角速度之比为 ,B错误;由于 、 两点角速度之比为 ,由 得, 、 两点转速之比为 , 、 两点转速相同,则 、 、 三点的转速之比为 ,C错误;由 可知, 、 两点的向心加速度之比为 ,由 可知, 、 两点的向心加速度之比为 ,所以 、 、 三点的向心加速度之比为 ,D正确.
6.【答案】D
【解析】设大轮半径为r1,小轮半径为r2,P、Q两点由皮带传动,所以=,P、S两点同轴转动,则ωP=ωS,根据线速度与角速度关系v=ωr,可知P、S两点的线速度关系为==,所以三点的线速度大小之比为3∶3∶1,选项A错误;P、Q两点角速度大小关系=·=,所以三点的角速度大小之比为1∶2∶1,选项B错误;根据ω=可知三点的周期之比为2∶1∶2,选项C错误;根据an=ω2r可知P、S两点的向心加速度大小之比=·=,根据an=可知P、Q两点的向心加速度大小之比=·=,所以三点的向心加速度大小之比为3∶6∶1,选项D正确.
7.【答案】A
【详解】
对小滑块向心力等于最大静摩擦力
μmg=mRω2
所以小圆盘转动的角速度为
A点的线速度为
所以B点的线速度大小为
则B点的角速度为
.
BCD错误,A正确。
故选A。
8.【答案】A
【详解】
AB.A、B两点是同缘转动,则线速度相等,即线速度大小之比
vA:vB=1:1
选项A正确,B错误;
C.根据
可知,A、B两点的角速度大小之比
ωA: ωB=1:2
选项C错误;
D.根据
可知,A、B两点的向心加速度大小之比
aA: aB=1:2
选项D错误。
故选A。
9.【答案】AD
【详解】由于 、 两点在同一竖直杆上,而且杆运动时始终保持竖直,所以在杆 绕 点从与水平方向成 匀速转动到 的过程中,两点都做半径相同的匀速圆周运动,故两点的线速度、角速度都相等,A正确,B错误;根据向心加速度等于角速度与线速度的乘积可知, 、 两点的向心加速度也相等,C错误;线速度相等,运动时间相等,则 、 两点的路程相等,D正确.
10.【答案】AD
【详解】质点A、B同轴,二者具有相同的角速度、周期和转速,即,,。并且有
质点B、C分通过皮带传动,二者具有相同的线速度,即,则有
A.根据以上分析可知,,故A正确。
B.根据以上分析可知,,故B错误。
C.根据以上分析可知,,故C错误
D.根据以上分析可知,,故D正确。
故选AD。
11.【答案】AD
【详解】 、 两点同轴转动,角速度大小相等,故A正确;由几何关系可知 、 的转动半径之比为 ,由线速度 可知 、 的线速度大小不相等,故B错误;根据向心加速度 可得, 、 的向心加速度大小之比为 ,故C错误,D正确.
12.【答案】 = 2:1 2:1
【详解】(1)[1]由于a、b轮半径相同,通过皮带传动线速度大小相同,故两槽转动的角速度满足
(2)[2]现有两个质量相同的钢球,球1放在A槽的横臂挡板处,球2放在B槽的横臂挡板处,它们到各自转轴的距离之比为2:1,由可知,钢球1、2的线速度之比为2:1。
[3]由向心力表达式可知,两钢球质量相同、转动角速度相同,则向心力大小与轨道半径成正比,故钢球1、2各自对应的标尺露出的格数之比为2:1。
13.【答案】 A A
【详解】(1)[1]本装置的原理是使物体质量、半径、角速度三个物理量其中的一个变化,控制其他物理量不变,从而研究向心力与各物理量之间的关系,故采用的是控制变量法;
(2)[2]根据可知,控制质量相同和半径相同,所以将质量相同的小球分别放在挡板C和挡板A处。
14.【答案】见解析
【详解】当人骑该车使脚踏板以恒定的角速度转动时,若不变换链轮,则飞轮边缘线速度不变;根据 可知,选择半径最小的飞轮,飞轮角速度最大,则后轮角速度最大,而后轮半径不变,则自行车行进的速度最大。
15.【答案】;
【详解】
B、C两点随同一个轮转动,角速度相等,A、B两点通过皮带传动,线速度大小相等,由
可得
可得
由
得
由
可得
则
16.【答案】(1);(2)
【详解】
(1)大齿轮的周期
则
大齿轮转动角速度的大小
(2)大齿轮和小齿轮边缘线速度的大小相等,有
解得小齿轮角速度的大小
小齿轮角速度与后轮角速度的大小相等,则后轮线速度的大小
第 page number 页,共 number of pages 页
第 page number 页,共 number of pages 页
同课章节目录
