1.3数轴 课件(共20张PPT) 2025-2026学年数学青岛版(2024)七年级上册
文档属性
| 名称 | 1.3数轴 课件(共20张PPT) 2025-2026学年数学青岛版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 521.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 10:06:35 | ||
图片预览





文档简介
(共20张PPT)
第1章 有理数
1.3 数轴
1.掌握数轴的概念,能正确的画出数轴;
2.理解数轴上的点和有理数的对应关系,会利用数轴上的点表示有理数.
在小学阶段,我们可以用直线上依次排列的点来表示自然数.
引入负数后,能否用类似的方式表示有理数呢?
1
2
3
4
5
某数学活动小组参加绘制北京地铁1号线的线路图的活动. 他们发现该地铁线呈东西走向,并测得王府井站和建国门站分别位于天安门西站东侧1.8km和3.8km处,西单站位于天安门西站西侧1.2km处.你能画图表示它们的位置吗?
如图,画一条直线表示北京地铁1号线,从左到右表示从西到东的方向.在直线上取一点O表示天安门西站的位置,规定1个单位长度(线段 OA 的长)代表1km的长度.
1km
O
西
东
A
天安门西站
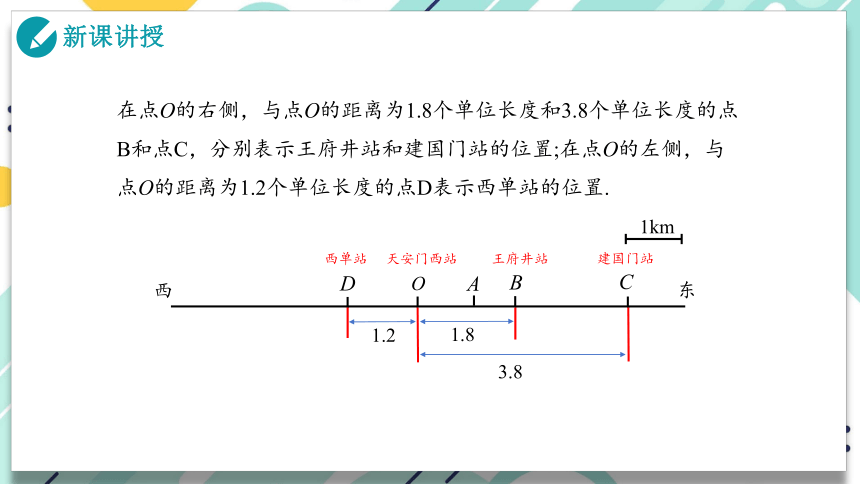
在点O的右侧,与点O的距离为1.8个单位长度和3.8个单位长度的点B和点C,分别表示王府井站和建国门站的位置;在点O的左侧,与点O的距离为1.2个单位长度的点D表示西单站的位置.
B
1.8
C
D
1km
O
西
东
A
天安门西站
王府井站
建国门站
西单站
1.2
3.8
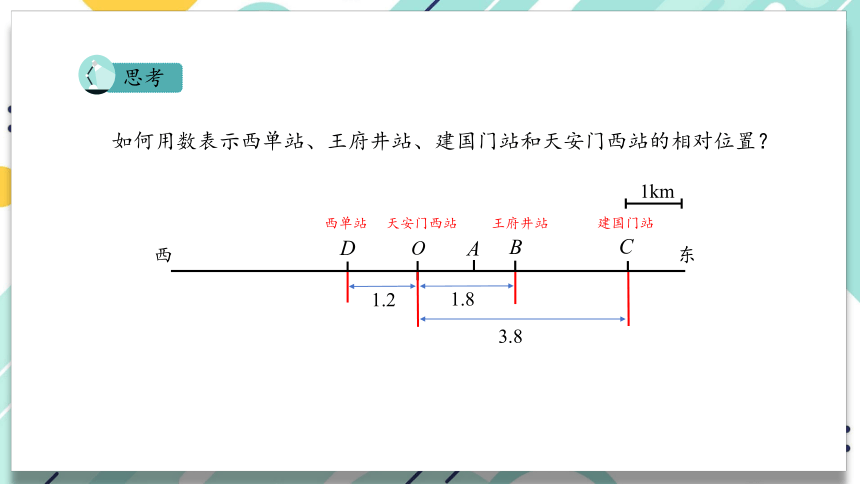
如何用数表示西单站、王府井站、建国门站和天安门西站的相对位置?
思考
B
1.8
C
D
1km
O
西
东
A
天安门西站
王府井站
建国门站
西单站
1.2
3.8
“东”与“西”、“左”与“右”具有相反意义. 我们可以用正数、负数和零分别表示各地铁站的相对位置.
如图,天安门西站的位置用0表示,规定向东为正,那么西单站的位置可以用-1.2表示,王府井站的位置可以用1.8表示,建国门站的位置可以用3.8表示.
B
1.8
C
D
O
西
东
A
-1.2
3.8
0
1
用直线上的点可以表示正数、0和负数,具体做法如下:
1.如图,画一条直线(一般把它画成水平的),在这条直线上任意取一点表示数0,这个点叫做原点.
2.规定自原点开始一侧的方向为正方向(习惯上取向右的方向为正方向),那么另一侧的方向就是负方向.
3.选取适当的长度为单位长度.
0
1
原点
2
3
4
5
1
2
3
4
5
正方向
单位长度
规定了原点、正方向和单位长度的直线叫做数轴.
4
0
1
2
1
2
3
3
4
数轴的特征
1.数轴是一条直线,向两端无限延伸.
2.数轴三要素:原点、正方向和单位长度.
1.画一条水平直线,定原点(如图),原点表示0.
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.
4.在原点左右两边依次标上对应的刻度数.
探索:数轴的画法:
0
1
2
4
1
2
3
3
4
正方向
例1 画出数轴,并用数轴上的点表示下列各数.
2,-2.5,0, ,-4.
解:如图所示.
4
0
1
2
1
2
3
3
4
-2.5
-4
2
0
通过例题我们可知正数,分数和小数都在可以在数轴上表示
你有什么发现呢?小组交流讨论.
4
0
1
2
1
2
3
3
4
-2.5
-4
2
0
建立了数轴,任何一个有理数都可以用数轴上的一个点表示出来.
数轴
概念:规定了原点、正方向和单位长度的直线叫做数轴.
2.数轴的画法.
数轴的特征
1.数轴是一条直线,向两端无限延伸.
2.数轴三要素:原点、正方向和单位长度.
1.下图中,是数轴的是( )
0
1
2
1
2
0
1
2
1
2
0
1
2
1
2
0
1
2
2
1
A.
B.
C.
D.
D
2.下列说法中,正确的是( )
A.数轴是一条规定了原点、正方向和单位长度的射线;
B.离原点近的点所表示的有理数较小;
C.数轴上的点可以表示任意有理数;
D.原点在数轴的正中间.
C
3.画出数轴,并用数轴上的点表示下列各数:
,-3 ,0 ,5 ,-4 ,- ,3 ,-5
解:如下图所示.
-3
0
5
-4
-5
3
4.有理数 a,b,c 在数轴上的位置如图所示,则 ( )
A. a,b,c 均是正数
B. a,b,c 均是负数
C. a,b 是正数,c 是负数
D. a,b 是负数,c 是正数
D
第1章 有理数
1.3 数轴
1.掌握数轴的概念,能正确的画出数轴;
2.理解数轴上的点和有理数的对应关系,会利用数轴上的点表示有理数.
在小学阶段,我们可以用直线上依次排列的点来表示自然数.
引入负数后,能否用类似的方式表示有理数呢?
1
2
3
4
5
某数学活动小组参加绘制北京地铁1号线的线路图的活动. 他们发现该地铁线呈东西走向,并测得王府井站和建国门站分别位于天安门西站东侧1.8km和3.8km处,西单站位于天安门西站西侧1.2km处.你能画图表示它们的位置吗?
如图,画一条直线表示北京地铁1号线,从左到右表示从西到东的方向.在直线上取一点O表示天安门西站的位置,规定1个单位长度(线段 OA 的长)代表1km的长度.
1km
O
西
东
A
天安门西站
在点O的右侧,与点O的距离为1.8个单位长度和3.8个单位长度的点B和点C,分别表示王府井站和建国门站的位置;在点O的左侧,与点O的距离为1.2个单位长度的点D表示西单站的位置.
B
1.8
C
D
1km
O
西
东
A
天安门西站
王府井站
建国门站
西单站
1.2
3.8
如何用数表示西单站、王府井站、建国门站和天安门西站的相对位置?
思考
B
1.8
C
D
1km
O
西
东
A
天安门西站
王府井站
建国门站
西单站
1.2
3.8
“东”与“西”、“左”与“右”具有相反意义. 我们可以用正数、负数和零分别表示各地铁站的相对位置.
如图,天安门西站的位置用0表示,规定向东为正,那么西单站的位置可以用-1.2表示,王府井站的位置可以用1.8表示,建国门站的位置可以用3.8表示.
B
1.8
C
D
O
西
东
A
-1.2
3.8
0
1
用直线上的点可以表示正数、0和负数,具体做法如下:
1.如图,画一条直线(一般把它画成水平的),在这条直线上任意取一点表示数0,这个点叫做原点.
2.规定自原点开始一侧的方向为正方向(习惯上取向右的方向为正方向),那么另一侧的方向就是负方向.
3.选取适当的长度为单位长度.
0
1
原点
2
3
4
5
1
2
3
4
5
正方向
单位长度
规定了原点、正方向和单位长度的直线叫做数轴.
4
0
1
2
1
2
3
3
4
数轴的特征
1.数轴是一条直线,向两端无限延伸.
2.数轴三要素:原点、正方向和单位长度.
1.画一条水平直线,定原点(如图),原点表示0.
2.规定从原点向右为正方向,那么相反的方向(从原点向左)则为负方向.
3.选择适当的长度为单位长度.
4.在原点左右两边依次标上对应的刻度数.
探索:数轴的画法:
0
1
2
4
1
2
3
3
4
正方向
例1 画出数轴,并用数轴上的点表示下列各数.
2,-2.5,0, ,-4.
解:如图所示.
4
0
1
2
1
2
3
3
4
-2.5
-4
2
0
通过例题我们可知正数,分数和小数都在可以在数轴上表示
你有什么发现呢?小组交流讨论.
4
0
1
2
1
2
3
3
4
-2.5
-4
2
0
建立了数轴,任何一个有理数都可以用数轴上的一个点表示出来.
数轴
概念:规定了原点、正方向和单位长度的直线叫做数轴.
2.数轴的画法.
数轴的特征
1.数轴是一条直线,向两端无限延伸.
2.数轴三要素:原点、正方向和单位长度.
1.下图中,是数轴的是( )
0
1
2
1
2
0
1
2
1
2
0
1
2
1
2
0
1
2
2
1
A.
B.
C.
D.
D
2.下列说法中,正确的是( )
A.数轴是一条规定了原点、正方向和单位长度的射线;
B.离原点近的点所表示的有理数较小;
C.数轴上的点可以表示任意有理数;
D.原点在数轴的正中间.
C
3.画出数轴,并用数轴上的点表示下列各数:
,-3 ,0 ,5 ,-4 ,- ,3 ,-5
解:如下图所示.
-3
0
5
-4
-5
3
4.有理数 a,b,c 在数轴上的位置如图所示,则 ( )
A. a,b,c 均是正数
B. a,b,c 均是负数
C. a,b 是正数,c 是负数
D. a,b 是负数,c 是正数
D
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
