1.4 相反数与绝对值 课件(共36张PPT) 2025-2026学年数学青岛版(2024)七年级上册
文档属性
| 名称 | 1.4 相反数与绝对值 课件(共36张PPT) 2025-2026学年数学青岛版(2024)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 518.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 10:05:19 | ||
图片预览











文档简介
(共36张PPT)
第1章 有理数
1.4 相反数与绝对值
第1章 有理数
1.4 课时1 相反数
1.掌握相反数的概念,理解互为相反数的两个数在数轴上的位置关系;
2.会求一个数的相反数,理解并掌握双重符号的化简方法.
什么是数轴?数轴的三要素是又是什么?
规定了原点、正方向和单位长度的直线叫做数轴.
数轴三要素:原点、正方向和单位长度.
观察4和-4,有什么不同点和相同点?
和呢?
数字相同
符号不同
只有符号不同的两个数叫做互为相反数.其中一个数叫做另一个数的相反数.
例如:4与-4互为相反数.-4的相反数是4,4的相反数是-4.
特别地,0的相反数是0.
一般地,a的相反数是-a,a可以是正数、负数,也可以是0.
当a=2时, 2的相反数是-2,即-a=-2.
当a=-2时,-2的相反数是2,即-(-2)=2.
表示一个数的相反数,可以在这个数的前面添一个“-”号.
-a不一定表示一个负数.
思考
(1)在数轴上画出表示4与-4的点,这两个点与原点有怎样的位置关系?
4
0
1
2
1
2
3
3
4
与原点的距离各是多少?
表示-与的点呢?
个单位
4个单位
4个单位
个单位
4
0
1
2
1
2
3
3
4
个单位
4个单位
4个单位
个单位
在数轴上,表示4与-4的两个点位于原点的两侧,并且与原点的距离相等;表示-与的两个点也一样.
思考
(2)将一个非零数与它的相反数分别用数轴上的点表示,这两点与原点之间有怎样的关系?
4
0
1
2
1
2
3
3
4
在数轴上,表示一个非零数与它的相反数的两个点分别位于原点两侧,并且与原点的距离相等.
例1 在数轴上表示下列各数及其相反数.
(1) 2; (2) -3.
解:2相反数是-2,-3的相反数是3.
0
1
2
3
-1
-2
-3
4
5
-4
-5
例2 化简:
(1) -(+); (2) -(-7.6).
解:(1) -(+)=-;
(2) -(-7.6)=7.6 .
双重符号化简的依据是相反数的概念.
相反数与绝对值
1.相反数的概念;
2.相反数的求法—在原数前面加负号“-”;
双重符号的化简.
a 的相反数是-a ,如-(+3)=-3,-(-3)=3,-0=0.
1.判断题
(1)-6 是 6 的相反数( );
(2)-5 是相反数( );
(3) 与 互为相反数( );
(4)-1 和 1 互为相反数( );
(5)相反数等于它本身的数只有 0 ﹙ ﹚;
(6)符号不同的两个数互为相反数﹙ ﹚.
×
√
×
√
√
×
2.写出下列各数.
(1)-3 的相反数; (2)0 的相反数;
(3)相反数是 的数; (4)相反数是-0.5的数.
解:(1)-3的相反数是3;
(2)0的相反数是0;
(3)相反数是 的数是 ;
(4)相反数是-0.5的数是0.5.
3.下列说法正确的是 ( )
A.正数和负数互为相反数;
B.0没有相反数;
C.在数轴上原点两旁的两个点表示的数互为相反数;
D.任何一个数都有它的相反数;
D
4.我们知道-a表示a的相反数,同理-(a-3)表示数(a-3) 的相反数.请根据相反数的意义,解决问题:若-[-(a-3)]和-[-(-8) ]互为相反数,求a的值.
a-3=8
a=11
所以a的值是11.
解:-[-(a-3) ]=a-3,-[-(-8)]=-8,
第1章 有理数
1.4 课时2 绝对值
1.理解绝对值的概念及其几何意义;
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.
0
1
2
3
4
-1
-2
-3
根据下面情景,回答问题:
大象距原点的距离为4个单位长度.
1.两只小狗分别距原点多远
2.大象距原点多远
两只小狗距原点的距离都是3个单位长度.
如图,在数轴上表示5与-5的点到原点的距离分别是多少?
表示-3与3的点呢?
0
1
2
3
-1
-2
-3
4
5
-4
-5
5
5
3
3
在数轴上,表示数a的点到原点的距离叫做这个数的绝对值.
记作|a|.
例如,数轴上表示5与-5的点到原点的距离均为5个单位长度,所以5和-5的绝对值都是5,即l5l=5,|-5l=5.
0
1
2
3
-1
-2
-3
4
5
-4
-5
5
5
思考
如果a表示有理数,那么│a│有什么含义?
答: ∣a∣表示数a的绝对值;
∣a∣表示数轴上数a对应的点与原点的距离.
思考
1.完成下列填空,你能从中发现什么
=______;
=_______;
=________;
=______;
=_______;
4
4
9.8
9.8
=________.
互为相反数的两个数的绝对值相等
一个数的绝对值是正数或0.
=______;
=_______;
=________;
=______;
=_______;
4
4
9.8
9.8
=________.
|a|
a , a>0
0, a=0
-a , a<0
正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.
注意:
1.任何一个有理数的绝对值都是非负数,即|a|≥0;
2.互为相反数的两个数的绝对值相等.
3.0到原点的距离是0,所以0的绝对值是0, 记作|0|=0.
例3 求绝对值等于7的数.
解:如图,到原点的距离为7的点有两个,即表示+7的点A和表示-7的点B,所以绝对值等于7的数是+7和-7.
0
1
2
3
-1
-2
-3
4
5
-4
-5
6
7
-6
-7
7个单位
7个单位
A
B
求一个数的绝对值的方法:
去掉绝对值符号时,必须按照“先判后去”的原则,先判断这个数是正数、0或负数,再根据绝对值的意义去掉绝对值符号,总之要确保其结果为非负数且只有一个.
=5
=7
=0
相反数与绝对值
概念
代数意义:
几何意义:在数轴上,表示数a的点与原点的距离 叫作数a的绝对值,记作|a|.
注意:
绝对值具有非负性,即|a|≥0.
1.下列说法中,错误的是 ( )
A. +5的绝对值等于5 B. 绝对值等于5的数是5
C. -5的绝对值是5 D. +5、-5的绝对值相等
B
2.有理数中绝对值等于它本身的数是( )
A. 0 B. 正数
C. 负数 D. 非负数
D
3.填空:
3
1.5
0
0.02
4.填空题
(1)表示 +7 的点与原点的距离是 个单位长度,即 +7 的绝值是___,记作 ;
(2)表示 2.8 的点与原点的距离是 个单位长度,即 2.8 的绝对值是____,记作 ;
(3)表示 -6 的点与原点的距离是 个单位长度,即 -6 的绝对值是_____,记作 ;
7
7
|7|
2.8
2.8
|2.8|
6
6
|-6|
5.计算:
(1)|-5|+|1.49|; (2)||÷||.
解:(1)原式=5+1.49=6.49;
(2)原式=÷ =11.
4.已知=0,求 x+y 的值.
解:根据题意可知
x-4=0,y-3=0
所以 x=4,y=3
故 x+y=7.
第1章 有理数
1.4 相反数与绝对值
第1章 有理数
1.4 课时1 相反数
1.掌握相反数的概念,理解互为相反数的两个数在数轴上的位置关系;
2.会求一个数的相反数,理解并掌握双重符号的化简方法.
什么是数轴?数轴的三要素是又是什么?
规定了原点、正方向和单位长度的直线叫做数轴.
数轴三要素:原点、正方向和单位长度.
观察4和-4,有什么不同点和相同点?
和呢?
数字相同
符号不同
只有符号不同的两个数叫做互为相反数.其中一个数叫做另一个数的相反数.
例如:4与-4互为相反数.-4的相反数是4,4的相反数是-4.
特别地,0的相反数是0.
一般地,a的相反数是-a,a可以是正数、负数,也可以是0.
当a=2时, 2的相反数是-2,即-a=-2.
当a=-2时,-2的相反数是2,即-(-2)=2.
表示一个数的相反数,可以在这个数的前面添一个“-”号.
-a不一定表示一个负数.
思考
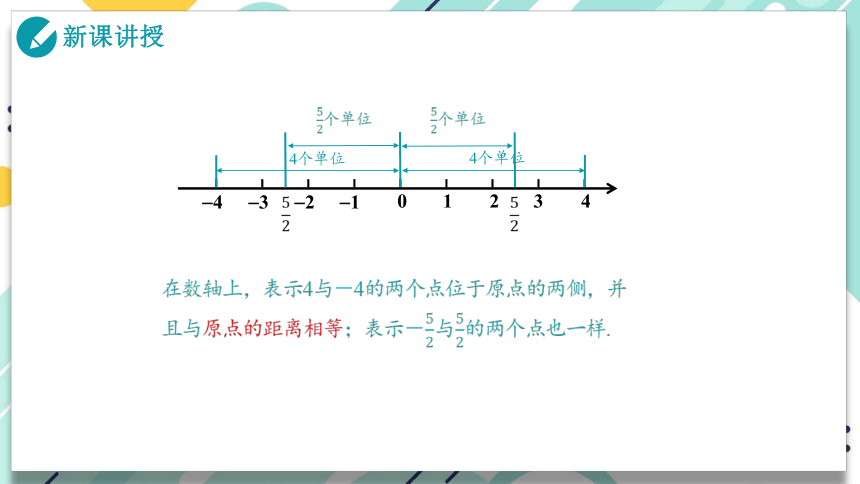
(1)在数轴上画出表示4与-4的点,这两个点与原点有怎样的位置关系?
4
0
1
2
1
2
3
3
4
与原点的距离各是多少?
表示-与的点呢?
个单位
4个单位
4个单位
个单位
4
0
1
2
1
2
3
3
4
个单位
4个单位
4个单位
个单位
在数轴上,表示4与-4的两个点位于原点的两侧,并且与原点的距离相等;表示-与的两个点也一样.
思考
(2)将一个非零数与它的相反数分别用数轴上的点表示,这两点与原点之间有怎样的关系?
4
0
1
2
1
2
3
3
4
在数轴上,表示一个非零数与它的相反数的两个点分别位于原点两侧,并且与原点的距离相等.
例1 在数轴上表示下列各数及其相反数.
(1) 2; (2) -3.
解:2相反数是-2,-3的相反数是3.
0
1
2
3
-1
-2
-3
4
5
-4
-5
例2 化简:
(1) -(+); (2) -(-7.6).
解:(1) -(+)=-;
(2) -(-7.6)=7.6 .
双重符号化简的依据是相反数的概念.
相反数与绝对值
1.相反数的概念;
2.相反数的求法—在原数前面加负号“-”;
双重符号的化简.
a 的相反数是-a ,如-(+3)=-3,-(-3)=3,-0=0.
1.判断题
(1)-6 是 6 的相反数( );
(2)-5 是相反数( );
(3) 与 互为相反数( );
(4)-1 和 1 互为相反数( );
(5)相反数等于它本身的数只有 0 ﹙ ﹚;
(6)符号不同的两个数互为相反数﹙ ﹚.
×
√
×
√
√
×
2.写出下列各数.
(1)-3 的相反数; (2)0 的相反数;
(3)相反数是 的数; (4)相反数是-0.5的数.
解:(1)-3的相反数是3;
(2)0的相反数是0;
(3)相反数是 的数是 ;
(4)相反数是-0.5的数是0.5.
3.下列说法正确的是 ( )
A.正数和负数互为相反数;
B.0没有相反数;
C.在数轴上原点两旁的两个点表示的数互为相反数;
D.任何一个数都有它的相反数;
D
4.我们知道-a表示a的相反数,同理-(a-3)表示数(a-3) 的相反数.请根据相反数的意义,解决问题:若-[-(a-3)]和-[-(-8) ]互为相反数,求a的值.
a-3=8
a=11
所以a的值是11.
解:-[-(a-3) ]=a-3,-[-(-8)]=-8,
第1章 有理数
1.4 课时2 绝对值
1.理解绝对值的概念及其几何意义;
2.会求一个有理数的绝对值,知道一个数的绝对值,会求这个数.
0
1
2
3
4
-1
-2
-3
根据下面情景,回答问题:
大象距原点的距离为4个单位长度.
1.两只小狗分别距原点多远
2.大象距原点多远
两只小狗距原点的距离都是3个单位长度.
如图,在数轴上表示5与-5的点到原点的距离分别是多少?
表示-3与3的点呢?
0
1
2
3
-1
-2
-3
4
5
-4
-5
5
5
3
3
在数轴上,表示数a的点到原点的距离叫做这个数的绝对值.
记作|a|.
例如,数轴上表示5与-5的点到原点的距离均为5个单位长度,所以5和-5的绝对值都是5,即l5l=5,|-5l=5.
0
1
2
3
-1
-2
-3
4
5
-4
-5
5
5
思考
如果a表示有理数,那么│a│有什么含义?
答: ∣a∣表示数a的绝对值;
∣a∣表示数轴上数a对应的点与原点的距离.
思考
1.完成下列填空,你能从中发现什么
=______;
=_______;
=________;
=______;
=_______;
4
4
9.8
9.8
=________.
互为相反数的两个数的绝对值相等
一个数的绝对值是正数或0.
=______;
=_______;
=________;
=______;
=_______;
4
4
9.8
9.8
=________.
|a|
a , a>0
0, a=0
-a , a<0
正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.
注意:
1.任何一个有理数的绝对值都是非负数,即|a|≥0;
2.互为相反数的两个数的绝对值相等.
3.0到原点的距离是0,所以0的绝对值是0, 记作|0|=0.
例3 求绝对值等于7的数.
解:如图,到原点的距离为7的点有两个,即表示+7的点A和表示-7的点B,所以绝对值等于7的数是+7和-7.
0
1
2
3
-1
-2
-3
4
5
-4
-5
6
7
-6
-7
7个单位
7个单位
A
B
求一个数的绝对值的方法:
去掉绝对值符号时,必须按照“先判后去”的原则,先判断这个数是正数、0或负数,再根据绝对值的意义去掉绝对值符号,总之要确保其结果为非负数且只有一个.
=5
=7
=0
相反数与绝对值
概念
代数意义:
几何意义:在数轴上,表示数a的点与原点的距离 叫作数a的绝对值,记作|a|.
注意:
绝对值具有非负性,即|a|≥0.
1.下列说法中,错误的是 ( )
A. +5的绝对值等于5 B. 绝对值等于5的数是5
C. -5的绝对值是5 D. +5、-5的绝对值相等
B
2.有理数中绝对值等于它本身的数是( )
A. 0 B. 正数
C. 负数 D. 非负数
D
3.填空:
3
1.5
0
0.02
4.填空题
(1)表示 +7 的点与原点的距离是 个单位长度,即 +7 的绝值是___,记作 ;
(2)表示 2.8 的点与原点的距离是 个单位长度,即 2.8 的绝对值是____,记作 ;
(3)表示 -6 的点与原点的距离是 个单位长度,即 -6 的绝对值是_____,记作 ;
7
7
|7|
2.8
2.8
|2.8|
6
6
|-6|
5.计算:
(1)|-5|+|1.49|; (2)||÷||.
解:(1)原式=5+1.49=6.49;
(2)原式=÷ =11.
4.已知=0,求 x+y 的值.
解:根据题意可知
x-4=0,y-3=0
所以 x=4,y=3
故 x+y=7.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
