1.5 有理数的大小 课件(13张PPT) 2025-2026学年数学青岛版(2024)七年级上册
文档属性
| 名称 | 1.5 有理数的大小 课件(13张PPT) 2025-2026学年数学青岛版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 08:06:02 | ||
图片预览





文档简介
(共13张PPT)
第一章 有理数
1.5 有理数的大小
1.掌握有理数大小的比较法则;(数形结合)
2.会比较有理数的大小,并能正确地使用“>”或“<”号连接;
3.能初步进行有理数大小比较的推理和书写.
学习目标
观察与发现:
1月某天,北京、济南、乌鲁木齐、兰州、上海这五个城市的最低气温如下表:
你能将五个城市的最低气温按从低到高的顺序排列吗?
五个城市的最低气温从低到高的顺序排列如下:-10,-6,-5,0,4
活动探究
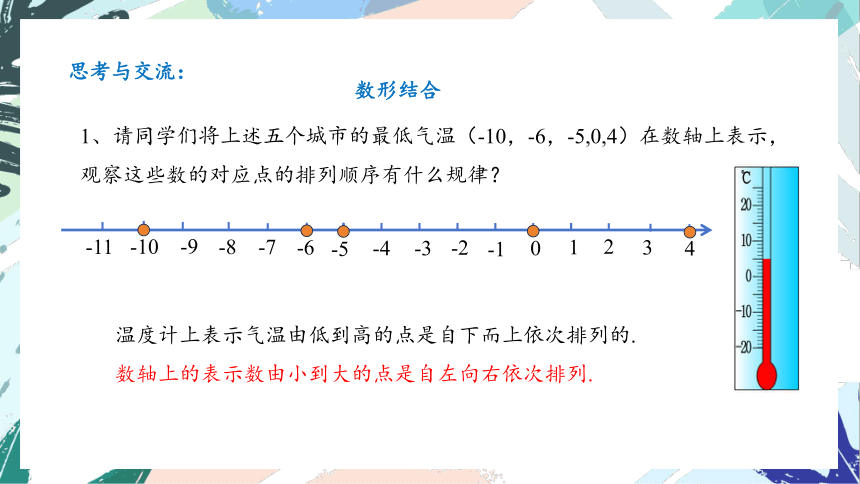
思考与交流:
1、请同学们将上述五个城市的最低气温(-10,-6,-5,0,4)在数轴上表示,观察这些数的对应点的排列顺序有什么规律?
0
1
2
3
-1
-2
-3
4
-4
-5
-6
-7
-8
-9
-10
-11
温度计上表示气温由低到高的点是自下而上依次排列的.
数轴上的表示数由小到大的点是自左向右依次排列.
数形结合
2、如何利用数轴比较有理数的大小?
0
1
2
3
-1
-2
-3
4
-4
-5
-6
-7
-8
-9
-10
-11
在数轴上右边的点所表示的数比左边的点所表示的数大.
3、对于正数、0、负数,它们之间存在怎样的大小关系?
4、两个负数的大小与他们的绝对值有什么关系?
正数大于0,负数小于0,正数大于负数.
例如:|-10|=10,|-6|=6,10>6 从数轴上可知-10<-6
两个负数,绝对值大的反而小.
思考与交流:
数形结合
概括与表达:
有理数大小比较方法:
① 在数轴上右边的点所表示的数比左边的点所表示的数大.
②正数大于0,负数小于0,正数大于负数.
③两个负数,绝对值大的反而小.
例1、比较下列各组中两个数的大小:
(1)3,-4; (2)-7.2,0; (3)-
解:(1)因为正数大于负数,所以3>-4;
(2)因为负数小于0,所以-7.2<0;
(3)因为 , ,
所以
典例精析
1、比较下面各对数的大小(填”<”,”>”或”=”),并说明理由.
①-20 -23 ② -3 ____+1 ③ - - ④ -1 ____0
2、表示a,b两数的点在数轴上的位置如图所示,a和b的大小关系是 .
<
>
① 在数轴上右边的点所表示的数比左边的点所表示的数大.
②正数大于0,负数小于0,正数大于负数.
③两个负数,绝对值大的反而小.
a<
<
a 0 b
巩固应用
3、将下列各数在数轴上表示出来,并按照由小到大的顺序用“<”把它们连起来:-4.5,0,-2,7,,
解:将这些数在数轴上分别用点表示出来,如图所示
-4.5
-2
0
7
由数轴上各点的位置可知,-4.5<-2< <0< <7
(4)因为 , ,
所以
1、利用数轴回答:
⑴有没有最大的整数和最小的整数?
⑵有没有最大的正整数和最小的正整数?
⑶有没有最大的负整数和最小的负整数?
2、有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.a>b B.|a|>|b| C.-a>b D.a>-b
D
当堂检测
3、如果 ,试比较 的大小.
解:因为
所以
因为 ,
所以 ,
所以 , ,
所以 .
0
a
b
-b
-a
学了本节课你有什么收获?
课堂总结
第一章 有理数
1.5 有理数的大小
1.掌握有理数大小的比较法则;(数形结合)
2.会比较有理数的大小,并能正确地使用“>”或“<”号连接;
3.能初步进行有理数大小比较的推理和书写.
学习目标
观察与发现:
1月某天,北京、济南、乌鲁木齐、兰州、上海这五个城市的最低气温如下表:
你能将五个城市的最低气温按从低到高的顺序排列吗?
五个城市的最低气温从低到高的顺序排列如下:-10,-6,-5,0,4
活动探究
思考与交流:
1、请同学们将上述五个城市的最低气温(-10,-6,-5,0,4)在数轴上表示,观察这些数的对应点的排列顺序有什么规律?
0
1
2
3
-1
-2
-3
4
-4
-5
-6
-7
-8
-9
-10
-11
温度计上表示气温由低到高的点是自下而上依次排列的.
数轴上的表示数由小到大的点是自左向右依次排列.
数形结合
2、如何利用数轴比较有理数的大小?
0
1
2
3
-1
-2
-3
4
-4
-5
-6
-7
-8
-9
-10
-11
在数轴上右边的点所表示的数比左边的点所表示的数大.
3、对于正数、0、负数,它们之间存在怎样的大小关系?
4、两个负数的大小与他们的绝对值有什么关系?
正数大于0,负数小于0,正数大于负数.
例如:|-10|=10,|-6|=6,10>6 从数轴上可知-10<-6
两个负数,绝对值大的反而小.
思考与交流:
数形结合
概括与表达:
有理数大小比较方法:
① 在数轴上右边的点所表示的数比左边的点所表示的数大.
②正数大于0,负数小于0,正数大于负数.
③两个负数,绝对值大的反而小.
例1、比较下列各组中两个数的大小:
(1)3,-4; (2)-7.2,0; (3)-
解:(1)因为正数大于负数,所以3>-4;
(2)因为负数小于0,所以-7.2<0;
(3)因为 , ,
所以
典例精析
1、比较下面各对数的大小(填”<”,”>”或”=”),并说明理由.
①-20 -23 ② -3 ____+1 ③ - - ④ -1 ____0
2、表示a,b两数的点在数轴上的位置如图所示,a和b的大小关系是 .
<
>
① 在数轴上右边的点所表示的数比左边的点所表示的数大.
②正数大于0,负数小于0,正数大于负数.
③两个负数,绝对值大的反而小.
a
<
a 0 b
巩固应用
3、将下列各数在数轴上表示出来,并按照由小到大的顺序用“<”把它们连起来:-4.5,0,-2,7,,
解:将这些数在数轴上分别用点表示出来,如图所示
-4.5
-2
0
7
由数轴上各点的位置可知,-4.5<-2< <0< <7
(4)因为 , ,
所以
1、利用数轴回答:
⑴有没有最大的整数和最小的整数?
⑵有没有最大的正整数和最小的正整数?
⑶有没有最大的负整数和最小的负整数?
2、有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.a>b B.|a|>|b| C.-a>b D.a>-b
D
当堂检测
3、如果 ,试比较 的大小.
解:因为
所以
因为 ,
所以 ,
所以 , ,
所以 .
0
a
b
-b
-a
学了本节课你有什么收获?
课堂总结
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
