3.6.2 共点力平衡的(共25张ppt)
文档属性
| 名称 | 3.6.2 共点力平衡的(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
粤教版 必修一 第三章
第三章 相互作用
第六节 共点力平衡
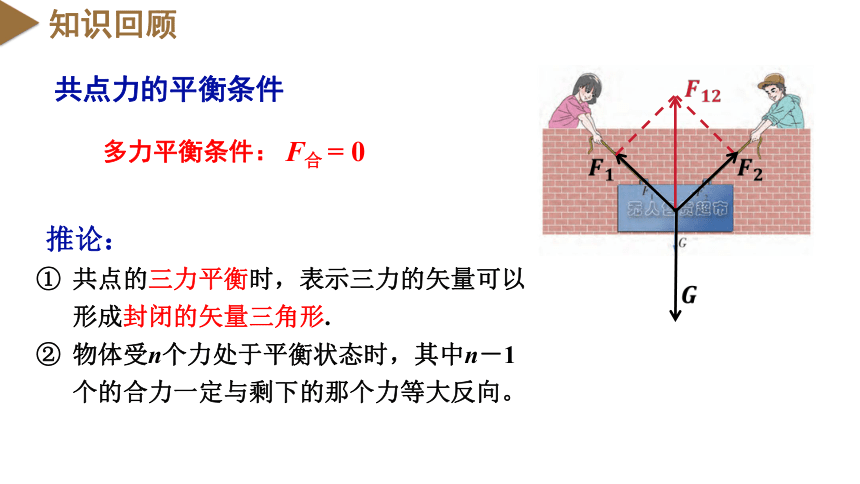
知识回顾
共点力的平衡条件
F合 = 0
多力平衡条件:
推论:
共点的三力平衡时,表示三力的矢量可以形成封闭的矢量三角形.
物体受n个力处于平衡状态时,其中n-1个的合力一定与剩下的那个力等大反向。
共点力平衡的解题步骤
1. 选取研究对象 ,判断是否是平衡状态;
2.隔离研究对象 ,分析物体的受力,画出受力图;
3.根据问题,合理选择合成法或分解法;
4.根据几何关系及平衡条件,列等式求解.
方法一:力的合成法
方法三:力的效果分解法
方法四:力的正交分解法(多力优选)
方法二:力的三角形法
1、“活结”与“死结”、
“动杆”与“定杆”问题
2、动态平衡问题
目录
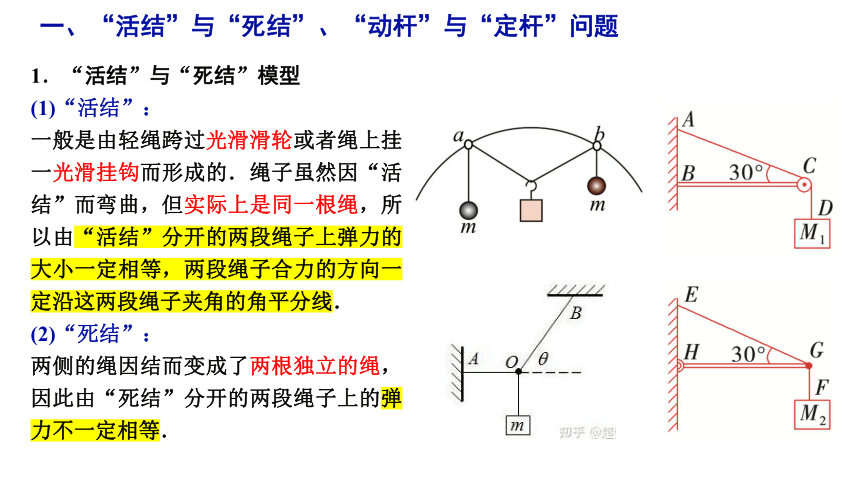
1.“活结”与“死结”模型
(1)“活结”:
一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线.
(2)“死结”:
两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等.
一、“活结”与“死结”、“动杆”与“定杆”问题
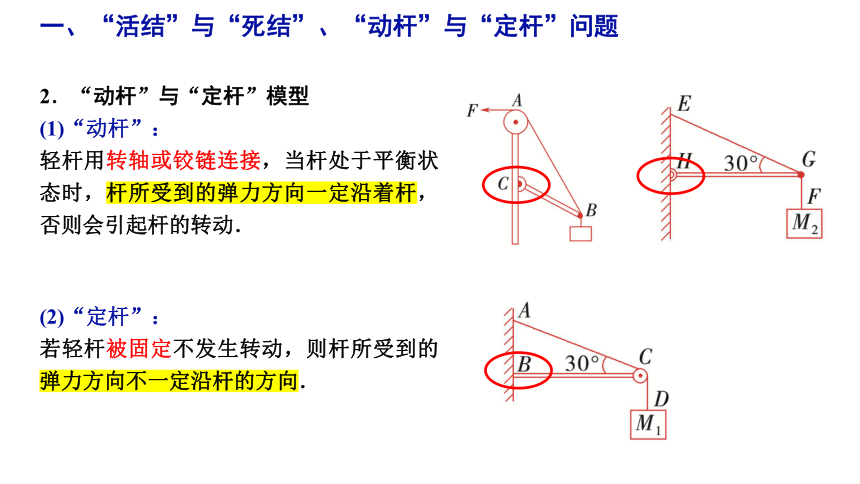
2.“动杆”与“定杆”模型
(1)“动杆”:
轻杆用转轴或铰链连接,当杆处于平衡状态时,杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.
一、“活结”与“死结”、“动杆”与“定杆”问题
(2)“定杆”:
若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.
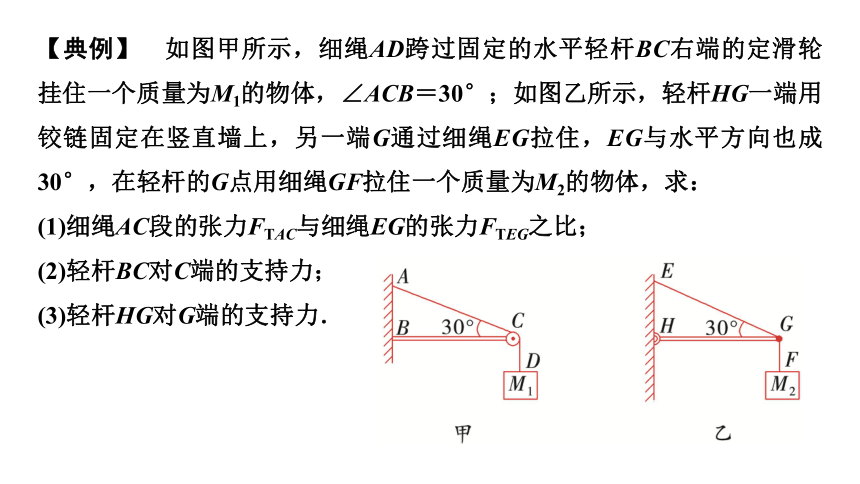
【典例】 如图甲所示,细绳AD跨过固定的水平轻杆BC右端的定滑轮挂住一个质量为M1的物体,∠ACB=30°;如图乙所示,轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,在轻杆的G点用细绳GF拉住一个质量为M2的物体,求:
(1)细绳AC段的张力FTAC与细绳EG的张力FTEG之比;
(2)轻杆BC对C端的支持力;
(3)轻杆HG对G端的支持力.
1.动态平衡:是指平衡问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,所以叫动态平衡,这是力平衡问题中的一类难题.
2.基本思路:化“动”为“静”,“静”中求“动”.
3.基本方法:解析法、矢量三角形法和相似三角形法.
二、动态平衡问题
4.处理动态平衡问题的一般步骤
(1)解析法(正交分解法)
①列平衡方程求出未知量与已知量的关系表达式.
②根据已知量的变化情况来确定未知量的变化情况.
(2) 矢量三角形法(图解法)
①适用情况:一般物体只受三个力作用,且其中一个力大小、方向均不变,另一个力的方向不变,第三个力的大小、方向均变化.
②一般步骤:
a.首先对物体进行受力分析,根据力的平行四边形定则将三个力的大小、方向放在同一个三角形中.
b.明确大小、方向不变的力,方向不变的力及方向变化的力的方向如何变化,画示意图.
③注意:由图解可知,当大小、方向都可变的分力(设为F1)与方向不变、大小可变的分力垂直时,F1有最小值.
【例1】如图,一盏电灯的重力大小为G,悬于水平天花板上的B点,在电线O处系一细线OA,使电线OB与竖直方向的夹角为β=37°,OA与水平方向成α角。现保持O点位置不变,使α角由0°缓慢增加到, ,,在此过程中( )
A.细线OA的拉力逐渐减小
B.电线OB的拉力逐渐减小
C.细线OA的拉力最小值为0.6G
D.细线OA的拉力最小值为0.8G
BC
【练习1】如图所示,两根等长的绳子AB和BC吊一重物静止,两根绳子与水平方向夹角均为60°.现保持绳子AB与水平方向的夹角不变,将绳子BC逐渐慢慢地拉到沿水平方向,在这一过程中,绳子BC的拉力变化情况是( )
A.增大
B.先减小后增大
C.减小
D.先增大后减小
B
【练习2】如图所示,光滑的轻质滑轮通过竖直杆固定于天花板上,一根不可伸长的轻绳跨过滑轮分别系着物块M和N,M静止在光滑水平地面上,N在水平拉力F作用下处于静止状态。现将F沿逆时针方向缓慢转至竖直方向,此过程中M和N始终静止不动。下列说法正确的是( )
A.F先增大后减小 B.绳的弹力先减小后增大
C.M对地面的压力逐渐减小 D.滑轮对杆的作用力逐渐减小
D
(3)相似三角形法
①适用情况:
在物体所受的三个力中,一个力是恒力,大小、方向均不变;
另外两个力是变力,大小、方向均改变,且方向不总是相互垂直
②解题技巧:
找到力变化过程中的几何关系,利用力的矢量三角形与几何三角形相似,相似三角形对应边成比例,通过分析几何三角形边长的变化得到表示力的边长的变化,从而得到力的变化.
【例2】如图所示,截面为四分之一圆的柱体放在墙脚,一个小球用细线拉着静止在光滑圆弧面上,细线的悬点在竖直墙面上A点,保持细线伸直长度不变,小球大小不计,将悬点沿竖直墙面缓慢向上移,在小球沿圆弧面向上缓慢移动过程中,下列判断正确的是( )
A.细线的拉力大小不变
B.细线的拉力减小
C.圆弧面对小球的支持力大小不变
D.圆弧面对小球的支持力增大
B
【练习3】如图所示,放在地面的大球始终不动,它的正上方有一个定滑轮,轻绳绕过定滑轮与光滑小球(可视为质点)相连,当用力F拉动轻绳,使小球沿大球表面从图示位置缓慢上滑到大球最高点的过程中,下列说法正确的是( )
A.小球受到的合力变大
B.地面对大球的摩擦力变大
C.小球受到的支持力大小不变,拉力F变小
D.拉力F不变,小球受到的支持力变小
C
(4)辅助圆法
①适用情况:
在物体所受的三个力中,一个力大小、方向均不变;
另外两个力的方向夹角θ不变
②解题技巧:
利用用圆的一根弦长表示恒力,该弦对应的圆周角大小不变。
通过分析圆内三角形边长的变化得到力的变化.
【例3】如图所示,倾斜直杆OM可以在竖直面内绕O点转动,轻绳AB的A端与套在直杆上的光滑轻环连接,绳子中间某点C拴一重物,用手拉住绳的另一端B。初始时BC水平,现将OM杆缓慢旋转到竖直,并保持∠ACB大小和轻环在杆上的位置不变,在OM转动过程中( )
A.绳AC的张力逐渐减小 B.绳AC的张力先减小后增大
C.绳BC的张力先增大后减小 D.绳BC的张力逐渐增大
AD
【例3】如图所示,倾斜直杆OM可以在竖直面内绕O点转动,轻绳AB的A端与套在直杆上的光滑轻环连接,绳子中间某点C拴一重物,用手拉住绳的另一端B。初始时BC水平,现将OM杆缓慢旋转到竖直,并保持∠ACB大小和轻环在杆上的位置不变,在OM转动过程中( )
A.绳AC的张力逐渐减小
B.绳AC的张力先减小后增大
C.绳BC的张力先增大后减小
D.绳BC的张力逐渐增大
AD
【练习4】
ACD
力的动态平衡问题
法一:矢量三角形法
法二:相似三角形法
法三:正交分解法
(解析法)
三力平衡时,一个力大小方向不变,
另一个力方向不变
三力平衡时,一个力大小方向不变,
另外两个力的方向都变化
且受力三角形与结构三角形相似
三个及以上的力平衡时
法四:辅助圆法
三力平衡时,一个力大小方向不变,
另外两个力的方向夹角θ不变
(用圆的一根弦长表示恒力)
【练习5】如图所示,一小球放置在木板与竖直墙面之间.设墙面对球的压力大小为FN1,木板对小球的支持力大小为FN2.以木板与墙连接点为轴,将木板从图示位置开始缓慢地转到水平位置.不计摩擦,在此过程中( )
A.FN1始终减小,FN2始终增大
B.FN1始终减小,FN2始终减小
C.FN1先增大后减小,FN2始终减小
D.FN1先增大后减小,FN2先减小后增大
B
B [解法一 解析法
对小球进行受力分析,如图甲所示,小球受重力G、墙面对小球的压力FN1、木板对小球的支持力FN2而处于平衡状态.从图甲中可以看出,FN1=,FN2=,从图示位置开始缓慢地转到水平位置过程中,θ逐渐增大,tan θ逐渐增大,sin θ逐渐增大,故FN1、FN2始终减小,故B正确.
甲
解法二 图解法
如图乙所示,小球受重力G、墙面对球的压力FN1、木板对小球的支持力FN2而处于平衡状态.由平衡条件知FN1、FN2的合力与G等大反向,θ增大时,画出多个平行四边形,由图乙可知在θ增大的过程中,FN1始终减小,FN2始终减小,故B正确.]
乙
【练习6】如图所示,光滑半球面上的小球(可视为质点)被一绕过光滑小定滑轮的轻绳在力F的作用下由底端缓慢拉到顶端的过程中,试分析F及半球面对小球的支持力FN的变化情况.
粤教版 必修一 第三章
第三章 相互作用
第六节 共点力平衡
知识回顾
共点力的平衡条件
F合 = 0
多力平衡条件:
推论:
共点的三力平衡时,表示三力的矢量可以形成封闭的矢量三角形.
物体受n个力处于平衡状态时,其中n-1个的合力一定与剩下的那个力等大反向。
共点力平衡的解题步骤
1. 选取研究对象 ,判断是否是平衡状态;
2.隔离研究对象 ,分析物体的受力,画出受力图;
3.根据问题,合理选择合成法或分解法;
4.根据几何关系及平衡条件,列等式求解.
方法一:力的合成法
方法三:力的效果分解法
方法四:力的正交分解法(多力优选)
方法二:力的三角形法
1、“活结”与“死结”、
“动杆”与“定杆”问题
2、动态平衡问题
目录
1.“活结”与“死结”模型
(1)“活结”:
一般是由轻绳跨过光滑滑轮或者绳上挂一光滑挂钩而形成的.绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线.
(2)“死结”:
两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等.
一、“活结”与“死结”、“动杆”与“定杆”问题
2.“动杆”与“定杆”模型
(1)“动杆”:
轻杆用转轴或铰链连接,当杆处于平衡状态时,杆所受到的弹力方向一定沿着杆,否则会引起杆的转动.
一、“活结”与“死结”、“动杆”与“定杆”问题
(2)“定杆”:
若轻杆被固定不发生转动,则杆所受到的弹力方向不一定沿杆的方向.
【典例】 如图甲所示,细绳AD跨过固定的水平轻杆BC右端的定滑轮挂住一个质量为M1的物体,∠ACB=30°;如图乙所示,轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EG与水平方向也成30°,在轻杆的G点用细绳GF拉住一个质量为M2的物体,求:
(1)细绳AC段的张力FTAC与细绳EG的张力FTEG之比;
(2)轻杆BC对C端的支持力;
(3)轻杆HG对G端的支持力.
1.动态平衡:是指平衡问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,所以叫动态平衡,这是力平衡问题中的一类难题.
2.基本思路:化“动”为“静”,“静”中求“动”.
3.基本方法:解析法、矢量三角形法和相似三角形法.
二、动态平衡问题
4.处理动态平衡问题的一般步骤
(1)解析法(正交分解法)
①列平衡方程求出未知量与已知量的关系表达式.
②根据已知量的变化情况来确定未知量的变化情况.
(2) 矢量三角形法(图解法)
①适用情况:一般物体只受三个力作用,且其中一个力大小、方向均不变,另一个力的方向不变,第三个力的大小、方向均变化.
②一般步骤:
a.首先对物体进行受力分析,根据力的平行四边形定则将三个力的大小、方向放在同一个三角形中.
b.明确大小、方向不变的力,方向不变的力及方向变化的力的方向如何变化,画示意图.
③注意:由图解可知,当大小、方向都可变的分力(设为F1)与方向不变、大小可变的分力垂直时,F1有最小值.
【例1】如图,一盏电灯的重力大小为G,悬于水平天花板上的B点,在电线O处系一细线OA,使电线OB与竖直方向的夹角为β=37°,OA与水平方向成α角。现保持O点位置不变,使α角由0°缓慢增加到, ,,在此过程中( )
A.细线OA的拉力逐渐减小
B.电线OB的拉力逐渐减小
C.细线OA的拉力最小值为0.6G
D.细线OA的拉力最小值为0.8G
BC
【练习1】如图所示,两根等长的绳子AB和BC吊一重物静止,两根绳子与水平方向夹角均为60°.现保持绳子AB与水平方向的夹角不变,将绳子BC逐渐慢慢地拉到沿水平方向,在这一过程中,绳子BC的拉力变化情况是( )
A.增大
B.先减小后增大
C.减小
D.先增大后减小
B
【练习2】如图所示,光滑的轻质滑轮通过竖直杆固定于天花板上,一根不可伸长的轻绳跨过滑轮分别系着物块M和N,M静止在光滑水平地面上,N在水平拉力F作用下处于静止状态。现将F沿逆时针方向缓慢转至竖直方向,此过程中M和N始终静止不动。下列说法正确的是( )
A.F先增大后减小 B.绳的弹力先减小后增大
C.M对地面的压力逐渐减小 D.滑轮对杆的作用力逐渐减小
D
(3)相似三角形法
①适用情况:
在物体所受的三个力中,一个力是恒力,大小、方向均不变;
另外两个力是变力,大小、方向均改变,且方向不总是相互垂直
②解题技巧:
找到力变化过程中的几何关系,利用力的矢量三角形与几何三角形相似,相似三角形对应边成比例,通过分析几何三角形边长的变化得到表示力的边长的变化,从而得到力的变化.
【例2】如图所示,截面为四分之一圆的柱体放在墙脚,一个小球用细线拉着静止在光滑圆弧面上,细线的悬点在竖直墙面上A点,保持细线伸直长度不变,小球大小不计,将悬点沿竖直墙面缓慢向上移,在小球沿圆弧面向上缓慢移动过程中,下列判断正确的是( )
A.细线的拉力大小不变
B.细线的拉力减小
C.圆弧面对小球的支持力大小不变
D.圆弧面对小球的支持力增大
B
【练习3】如图所示,放在地面的大球始终不动,它的正上方有一个定滑轮,轻绳绕过定滑轮与光滑小球(可视为质点)相连,当用力F拉动轻绳,使小球沿大球表面从图示位置缓慢上滑到大球最高点的过程中,下列说法正确的是( )
A.小球受到的合力变大
B.地面对大球的摩擦力变大
C.小球受到的支持力大小不变,拉力F变小
D.拉力F不变,小球受到的支持力变小
C
(4)辅助圆法
①适用情况:
在物体所受的三个力中,一个力大小、方向均不变;
另外两个力的方向夹角θ不变
②解题技巧:
利用用圆的一根弦长表示恒力,该弦对应的圆周角大小不变。
通过分析圆内三角形边长的变化得到力的变化.
【例3】如图所示,倾斜直杆OM可以在竖直面内绕O点转动,轻绳AB的A端与套在直杆上的光滑轻环连接,绳子中间某点C拴一重物,用手拉住绳的另一端B。初始时BC水平,现将OM杆缓慢旋转到竖直,并保持∠ACB大小和轻环在杆上的位置不变,在OM转动过程中( )
A.绳AC的张力逐渐减小 B.绳AC的张力先减小后增大
C.绳BC的张力先增大后减小 D.绳BC的张力逐渐增大
AD
【例3】如图所示,倾斜直杆OM可以在竖直面内绕O点转动,轻绳AB的A端与套在直杆上的光滑轻环连接,绳子中间某点C拴一重物,用手拉住绳的另一端B。初始时BC水平,现将OM杆缓慢旋转到竖直,并保持∠ACB大小和轻环在杆上的位置不变,在OM转动过程中( )
A.绳AC的张力逐渐减小
B.绳AC的张力先减小后增大
C.绳BC的张力先增大后减小
D.绳BC的张力逐渐增大
AD
【练习4】
ACD
力的动态平衡问题
法一:矢量三角形法
法二:相似三角形法
法三:正交分解法
(解析法)
三力平衡时,一个力大小方向不变,
另一个力方向不变
三力平衡时,一个力大小方向不变,
另外两个力的方向都变化
且受力三角形与结构三角形相似
三个及以上的力平衡时
法四:辅助圆法
三力平衡时,一个力大小方向不变,
另外两个力的方向夹角θ不变
(用圆的一根弦长表示恒力)
【练习5】如图所示,一小球放置在木板与竖直墙面之间.设墙面对球的压力大小为FN1,木板对小球的支持力大小为FN2.以木板与墙连接点为轴,将木板从图示位置开始缓慢地转到水平位置.不计摩擦,在此过程中( )
A.FN1始终减小,FN2始终增大
B.FN1始终减小,FN2始终减小
C.FN1先增大后减小,FN2始终减小
D.FN1先增大后减小,FN2先减小后增大
B
B [解法一 解析法
对小球进行受力分析,如图甲所示,小球受重力G、墙面对小球的压力FN1、木板对小球的支持力FN2而处于平衡状态.从图甲中可以看出,FN1=,FN2=,从图示位置开始缓慢地转到水平位置过程中,θ逐渐增大,tan θ逐渐增大,sin θ逐渐增大,故FN1、FN2始终减小,故B正确.
甲
解法二 图解法
如图乙所示,小球受重力G、墙面对球的压力FN1、木板对小球的支持力FN2而处于平衡状态.由平衡条件知FN1、FN2的合力与G等大反向,θ增大时,画出多个平行四边形,由图乙可知在θ增大的过程中,FN1始终减小,FN2始终减小,故B正确.]
乙
【练习6】如图所示,光滑半球面上的小球(可视为质点)被一绕过光滑小定滑轮的轻绳在力F的作用下由底端缓慢拉到顶端的过程中,试分析F及半球面对小球的支持力FN的变化情况.
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
