4.3 牛顿第二定律(共13张ppt)
文档属性
| 名称 | 4.3 牛顿第二定律(共13张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 22:07:15 | ||
图片预览




文档简介
(共13张PPT)
粤教版 必修一 第四章
第四章 牛顿运动定律
第三节 牛顿第二定律
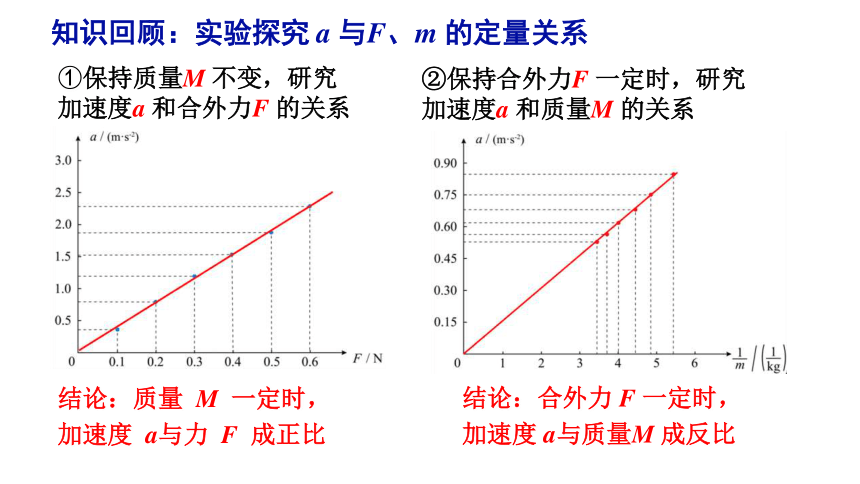
①保持质量M 不变,研究加速度a 和合外力F 的关系
知识回顾:实验探究 a 与F、m 的定量关系
结论:质量 M 一定时,加速度 a与力 F 成正比
②保持合外力F 一定时,研究加速度a 和质量M 的关系
结论:合外力 F 一定时,
加速度 a与质量M 成反比
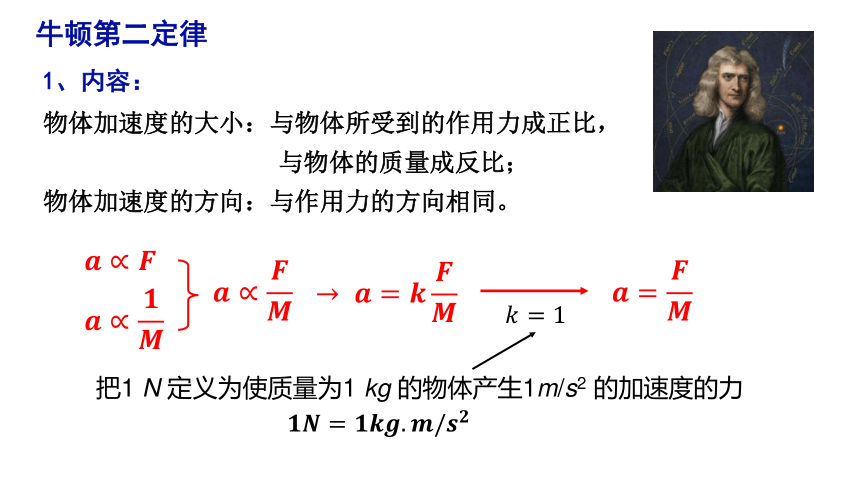
牛顿第二定律
物体加速度的大小:与物体所受到的作用力成正比,
与物体的质量成反比;
物体加速度的方向:与作用力的方向相同。
1、内容:
把1 N 定义为使质量为1 kg 的物体产生1m/s2 的加速度的力
牛顿第二定律
2、数学表达式:
思考与讨论:
根据牛顿第二定律,力能使物体产生加速度,但为什么我们经常用很大力提一个很重的物体时,我们却提不动它。这是否违背牛顿第二定律?为什么?
※物体受到的力往往不只一个,方程中的F指物体所受外力的合力
3. 矢量性:F=ma是一个矢量式,a与F 的方向总是相同;
2. 同体性: a 、F、m对应于同一物体;
1.因果性:力是产生加速度的原因,合外力不为零时一定有加速度;
对牛顿第二定律的理解
课堂练习
4. 瞬时性(同时性): a与F是瞬时对应关系(含大小和方向),即a与F同时产生,同时变化,同时消失。加速度与力一样可以突变,而速度是无法突变的;
2.分析受力情况
画受力分析图
求合
外力
求a
3.运动情况的分析
选择合适的运动学表达式
4.根据牛顿第二定律 F合 =ma 列方程求解
桥梁:
加速度a
1.选择研究对象
解牛顿第二定律的问题的一般步骤
课堂练习
方法1:合成法
a
方法2——正交分解法
mg
FT
y
x
Fx
Fy
竖直方向
水平方向
FT sin θ = ma (2)
FT cos θ = mg (1)
两式联立,求得小球的加速度为:
a=g tan θ 方向水平向右
小球在水平方向上做匀加速直线运动,在竖直方向上处于平衡状态。
3. 矢量性:F=ma是一个矢量式,a与F 的方向总是相同;
4. 瞬时性(同时性): a与F是瞬时对应关系(含大小和方向),即a与F同时产生,同时变化,同时消失。加速度与力一样可以突变,而速度是无法突变的;
5. 独立性:每个力各自独立地能使物体产生一个加速度,与物体是否受其他力无关。力和加速度在各个方向上的分量也遵循牛顿第二定律,即:Fx=max;Fy=may
2. 同体性: a 、F、m对应于同一物体;
1.因果性:力是产生加速度的原因,合外力不为零时一定有加速度;
对牛顿第二定律的理解
课堂练习
如图所示,一木块沿倾角θ=37°的光滑固定斜面自由下滑.
g取10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求木块的加速度大小;
(2)若木块与斜面间的动摩擦因数μ=0.5,求木块加速度的大小.
[答案] (1)6 m/s2 (2)2 m/s2
[解析] (1)分析木块的受力情况如图甲所示,
木块受重力mg、支持力FN两个力作用,
合外力大小为mg sin θ,
根据牛顿第二定律得mg sin θ=ma1
所以a1=g sin θ=10×0.6 m/s2=6 m/s2.
甲
(2)若斜面粗糙,木块的受力情况如图乙所示,建立直角坐标系.
在x方向上(沿斜面方向)
mg sin θ-Ff=ma2 ①
在y方向上(垂直斜面方向)
FN=mg cos θ ②
又因为Ff=μFN ③
由①②③得a2=g sin θ-μg cos θ=(10×0.6-0.5×10×0.8)m/s2=2 m/s2.
乙
粤教版 必修一 第四章
第四章 牛顿运动定律
第三节 牛顿第二定律
①保持质量M 不变,研究加速度a 和合外力F 的关系
知识回顾:实验探究 a 与F、m 的定量关系
结论:质量 M 一定时,加速度 a与力 F 成正比
②保持合外力F 一定时,研究加速度a 和质量M 的关系
结论:合外力 F 一定时,
加速度 a与质量M 成反比
牛顿第二定律
物体加速度的大小:与物体所受到的作用力成正比,
与物体的质量成反比;
物体加速度的方向:与作用力的方向相同。
1、内容:
把1 N 定义为使质量为1 kg 的物体产生1m/s2 的加速度的力
牛顿第二定律
2、数学表达式:
思考与讨论:
根据牛顿第二定律,力能使物体产生加速度,但为什么我们经常用很大力提一个很重的物体时,我们却提不动它。这是否违背牛顿第二定律?为什么?
※物体受到的力往往不只一个,方程中的F指物体所受外力的合力
3. 矢量性:F=ma是一个矢量式,a与F 的方向总是相同;
2. 同体性: a 、F、m对应于同一物体;
1.因果性:力是产生加速度的原因,合外力不为零时一定有加速度;
对牛顿第二定律的理解
课堂练习
4. 瞬时性(同时性): a与F是瞬时对应关系(含大小和方向),即a与F同时产生,同时变化,同时消失。加速度与力一样可以突变,而速度是无法突变的;
2.分析受力情况
画受力分析图
求合
外力
求a
3.运动情况的分析
选择合适的运动学表达式
4.根据牛顿第二定律 F合 =ma 列方程求解
桥梁:
加速度a
1.选择研究对象
解牛顿第二定律的问题的一般步骤
课堂练习
方法1:合成法
a
方法2——正交分解法
mg
FT
y
x
Fx
Fy
竖直方向
水平方向
FT sin θ = ma (2)
FT cos θ = mg (1)
两式联立,求得小球的加速度为:
a=g tan θ 方向水平向右
小球在水平方向上做匀加速直线运动,在竖直方向上处于平衡状态。
3. 矢量性:F=ma是一个矢量式,a与F 的方向总是相同;
4. 瞬时性(同时性): a与F是瞬时对应关系(含大小和方向),即a与F同时产生,同时变化,同时消失。加速度与力一样可以突变,而速度是无法突变的;
5. 独立性:每个力各自独立地能使物体产生一个加速度,与物体是否受其他力无关。力和加速度在各个方向上的分量也遵循牛顿第二定律,即:Fx=max;Fy=may
2. 同体性: a 、F、m对应于同一物体;
1.因果性:力是产生加速度的原因,合外力不为零时一定有加速度;
对牛顿第二定律的理解
课堂练习
如图所示,一木块沿倾角θ=37°的光滑固定斜面自由下滑.
g取10 m/s2,sin 37°=0.6,cos 37°=0.8.
(1)求木块的加速度大小;
(2)若木块与斜面间的动摩擦因数μ=0.5,求木块加速度的大小.
[答案] (1)6 m/s2 (2)2 m/s2
[解析] (1)分析木块的受力情况如图甲所示,
木块受重力mg、支持力FN两个力作用,
合外力大小为mg sin θ,
根据牛顿第二定律得mg sin θ=ma1
所以a1=g sin θ=10×0.6 m/s2=6 m/s2.
甲
(2)若斜面粗糙,木块的受力情况如图乙所示,建立直角坐标系.
在x方向上(沿斜面方向)
mg sin θ-Ff=ma2 ①
在y方向上(垂直斜面方向)
FN=mg cos θ ②
又因为Ff=μFN ③
由①②③得a2=g sin θ-μg cos θ=(10×0.6-0.5×10×0.8)m/s2=2 m/s2.
乙
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
