4.5 牛顿第二定律的应用(共29张ppt)
文档属性
| 名称 | 4.5 牛顿第二定律的应用(共29张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 22:08:09 | ||
图片预览








文档简介
(共29张PPT)
粤教版 必修一 第四章
第四章 牛顿运动定律
第五节 牛顿第二定律的应用
牛顿第二定律
物体加速度的大小:与物体所受到的作用力成正比,
与物体的质量成反比;
物体加速度的方向:与作用力的方向相同。
1、内容:
2、数学表达式:
F 指物体所受外力的合力
1、瞬时加速度问题
2、从运动情况确定受力
目录
3、由受力确定运动情况
Part 01
瞬时加速度问题
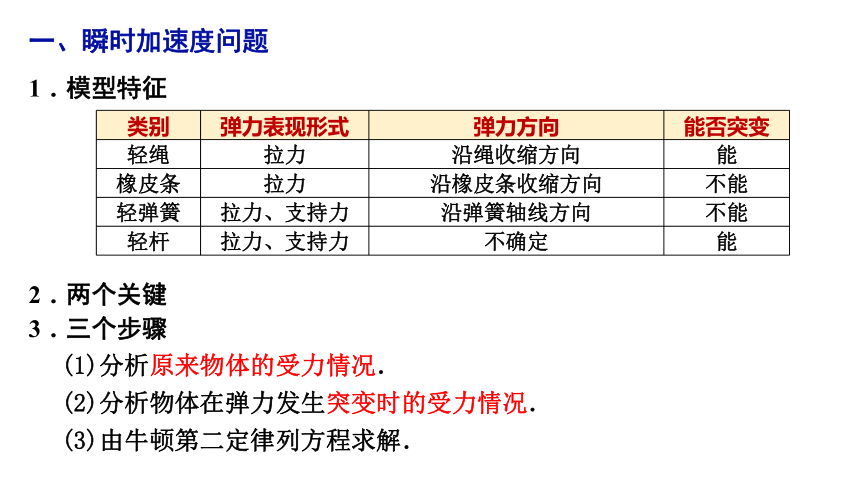
一、瞬时加速度问题
1.模型特征
类别 弹力表现形式 弹力方向 能否突变
轻绳 拉力 沿绳收缩方向 能
橡皮条 拉力 沿橡皮条收缩方向 不能
轻弹簧 拉力、支持力 沿弹簧轴线方向 不能
轻杆 拉力、支持力 不确定 能
2.两个关键
3.三个步骤
(1)分析原来物体的受力情况.
(2)分析物体在弹力发生突变时的受力情况.
(3)由牛顿第二定律列方程求解.
【典例1】 (多选)如图所示,质量为m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小为T1,Ⅱ中拉力大小为T 2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )
A.若剪断Ⅰ,则a=g,竖直向下
B.若剪断Ⅱ,则a=,方向水平向左
C.若剪断Ⅰ,则a=,方向沿Ⅰ的延长线
D.若剪断Ⅱ,则a=g,竖直向上
AB [绳子未断时,受力如图甲所示,
由共点力平衡条件得T 2=mg tan θ,T1= .
刚剪断弹簧Ⅰ瞬间,细线弹力突变为0,
故小球只受重力,加速度为g,竖直向下,故A正确,C错误;
刚剪断细线瞬间,弹簧弹力和重力不变,受力如图乙所示,
则F合=T1sin θ=T 2=ma,因而a==,方向水平向左,
故B正确,D错误.]
思路点拨:
①剪断水平线Ⅱ瞬间,弹簧拉力来不及恢复.
②剪断轻弹簧瞬间,轻弹簧的形变量能瞬间恢复,细线的弹力能突变为0
规律方法 两类模型的形变特点
(1)刚性绳模型(细钢丝、细绳、轻杆等):
这类形变的发生和变化过程极短,在物体的受力情况改变(如某个力消失)的瞬间,其形变可随之突变,弹力可以突变.
(2)轻弹簧模型(轻弹簧、橡皮绳、弹性绳等):
此类形变发生改变需要的时间较长,在瞬间问题中,其弹力的大小不能突变,可看成是不变的.但如果剪断轻弹簧、橡皮绳、弹性绳本身,则形变可瞬间恢复.
[课堂练习]
1.A、B两个球用轻弹簧连接,A球质量为2m,B球质量为3m,小球A由轻绳悬挂在天花板上O点,两球处于平衡状态,如图所示。现突然剪断轻绳OA,让小球下落,在剪断轻绳的瞬间,设小球A、B的加速度分别用a1和a2表示,则( )
A.a1 = g,a2 = g
B.a1 = 0,a2 = 2g
C.a1 = 2.5g,a2 = 0
D.a1 = 1.5g,a2 = 0
C 【详解】
剪断轻绳之前,对B进行分析,
弹簧处于拉伸状态,弹簧拉力大小
剪断轻绳的瞬间,分别对A、B进行分析,
根据牛顿第二定律有 ,
解得,
故选C。
[课堂练习]
2.用两根细线a、b和一个轻弹簧将两个相同的小球1和2连接并悬挂,如图所示.两小球处于静止状态,轻弹簧水平,重力加速度为g。
剪断细线b的瞬间( )
A.球1加速度大小小于g
B.球2加速度大小等于g
C.球1加速度方向竖直向下
D.球2加速度方向水平向右
A 【详解】A.设a与竖直方向的夹角为,
剪断细线b的瞬间,a绳弹力发生突变,
小球1 所受合力为
解得小球1的加速度大小为 故A正确;
B.小球1与2组成的整体,由平衡条件可得 ,
以小球2为对象,细线b对小球2的拉力大小为
剪断细线b的瞬间,弹簧c弹力不变,
小球2的合力大小为
根据牛顿第二定律可得
解得小球2的加速度大小大于,故B错误;
C.球1加速度方向与绳a垂直,故C错误;
D.球2加速度方向斜向右下方,故D错误。故选A。
[课堂练习]
3.(多选)如图所示,甲乙两图中A、B两球质量相等,图甲中A、B两球用轻质杆相连,图乙中A、B两球用轻质弹簧相连,均用细绳悬挂在天花板下处于静止状态,则在两细绳烧断的瞬间( )
A.图甲中轻杆的作用力为零
B.图甲中两球的加速度一定相等
C.图乙中两球的加速度一定相等
D.图甲中A球的加速度是图乙中A球加速度的一半
ABD [设两球质量均为m,细绳烧断的瞬间弹簧弹力不能突变,而杆的弹力会突变,所以细绳烧断瞬间,题图乙中B球所受合力仍为零,加速度为零,A球所受合力为2mg,加速度为2g;题图甲中,细绳烧断瞬间,A、B的加速度相同,设为a.以整体为研究对象,根据牛顿第二定律得2mg=2ma,得a=g,设题图甲中轻杆的作用力为T,再以B球为研究对象,由牛顿第二定律得mg+T=ma,解得T=0,即题图甲中轻杆的作用力一定为零,故A、B、D正确,C错误.]
2.分析受力情况
画受力分析图
求合
外力
求a
3.运动情况的分析
选择合适的运动学表达式
桥梁:
加速度a
1.选择研究对象
解牛顿第二定律的问题的一般步骤
F合 =ma
Part 02
从运动情况确定受力
二、从运动情况确定受力
1.基本思路:本类型问题是解决考点2中问题的逆过程,其思路如下:
2.解题步骤
(1)确定研究对象,对研究对象进行受力分析和运动过程分析,并画出受力示意图和运动草图.
(2)选择合适的运动学公式,求出物体的加速度.
(3)根据牛顿第二定律列方程,求物体所受的合外力.
(4)根据力的合成与分解的方法,由合力求出所需的力.
例题1
一列静止在站台上的火车,总质量为出发时间到了,这列火车从站台缓缓开出,1 min 20 s 后显示其速度达到. 若火车做匀加速直线运动,求火车在加速过程中的合力要多大才能满足加速的要求
例题1
一列静止在站台上的火车,总质量为出发时间到了,这列火车从站台缓缓开出,1 min 20 s 后显示其速度达到. 若火车做匀加速直线运动,求火车在加速过程中的合力要多大才能满足加速的要求
变式:若已知火车受到的阻力是车重的0.05 倍,那么这时火车所需要的牵引力应为多大?
[课堂练习]
1.如图所示的机车,质量为100 t,设它从停车场出发经225 m后速度达到15 m/s(该过程为匀加速直线运动),此时司机关闭发动机,让机车进站,机车又行驶了125 m才停在站上,设机车所受的阻力保持不变,求:
(1)机车在加速阶段和减速阶段的加速度大小;
(2)机车关闭发动机前所受的牵引力大小.
[解析] (1)设机车在加速、减速阶段的加速度大小分别为a1和a2,根据运动学公式可得2a1s1=v2,-2a2s2=
解得a1=0.5 m/s2,a2=0.9 m/s2.
(2)由牛顿第二定律得
F-f=ma1,f=ma2
解得F=1.4×105 N.
[答案] (1)0.5 m/s2 0.9 m/s2 (2)1.4×105 N
[课堂练习]
2、如图所示,截面为直角三角形的木块置于粗糙的水平地面上,其倾角θ=30°.现木块上有一质量m=1.0 kg的滑块从斜面下滑,测得滑块在0.40 s内速度增加了1.4 m/s,且知滑块滑行过程中木块处于静止状态,重力加速度g取10 m/s2,求:
(1)滑块滑行过程中受到的摩擦力大小;
(2)滑块滑行过程中木块受到地面的摩擦力大小及方向.
[解析] (1)由题意可知,滑块滑行的加速度
a== m/s2=3.5 m/s2
对滑块受力分析,如图甲所示,根据牛顿
第二定律得mg sin θ-f=ma,解得f=1.5 N。
(2)根据(1)问中的滑块受力示意图可得FN=mg cos θ.对木块受力分析,如图乙所示,根据牛顿第三定律有FN′=FN,f ′=f,根据水平方向上的平衡条件可得
f地+f′cos θ=FN′sin θ,解得f地≈3.03 N,f地为正值,说明图中标出的方向符合实际,故摩擦力方向水平向左.
[答案] (1)1.5 N (2)3.03 N 方向水平向左
甲 乙
Part 03
由受力确定运动情况
三、由受力确定运动情况
1.解题思路:
2.解题步骤
(1)确定研究对象,对研究对象进行受力分析,并画出物体的受力示意图.
(2)根据力的合成与分解,求出物体所受的合外力(包括大小和方向).
(3)根据牛顿第二定律列方程,求出物体运动的加速度.
(4)结合物体运动的初始条件,选择运动学公式,求出所需求的运动学量
——任意时刻的位移和速度,以及运动轨迹等.
课后练习1:
如图,沿倾角为θ的斜面向上拉一个质量为m的方木箱,拉力F与斜面平行,木箱与斜面的动摩擦因数为μ ,木箱沿斜面向上运动的距离为s.
(1) 画出木箱所受到的力的示意图.
(2) 写出合力的表达式.
(3) 求木箱通过距离s 所用的时间t.
教材例题2 某市交通部门规定汽车在市区某些街道的行驶速度不得超过. 一辆汽车在该水平路段紧急刹车时车轮抱死,沿直线滑行一段距离后停止.交警测得车轮在地面上滑行的轨迹长 ,从手册中查出该车轮与地面间的动摩擦因数.
试通过计算判断该汽车是否违反规定超速行驶.(取)
[课堂练习] 如图甲所示,质量为4 kg的物体放在与水平面成30°角、足够长的粗糙斜面上,物体与斜面间的动摩擦因数μ=,作用在物体上的外力与斜面平行,随时间变化的图像如图乙所示,外力作用在物体上的时间共8 s,根据所给条件(sin 30°=,cos 30°=,g取10 m/s2)问:
(1)物体所受的摩擦阻力为多大?
(2)物体在0~4 s内的加速度为多大?运动的位移为多大?
甲 乙
[解析] (1)如图,对物体进行受力分析可得:
G1=mg sin 30°=20 N
FN=G2=mg cos 30°=20 N
Ff=μFN=×20 N=20 N.
(2)由牛顿第二定律可得,0~4 s内物体的加速度为
a==5 m/s2
0~4 s内位移s1=at2=40 m.
[答案] (1)20 N (2)5 m/s2 40 m
粤教版 必修一 第四章
第四章 牛顿运动定律
第五节 牛顿第二定律的应用
牛顿第二定律
物体加速度的大小:与物体所受到的作用力成正比,
与物体的质量成反比;
物体加速度的方向:与作用力的方向相同。
1、内容:
2、数学表达式:
F 指物体所受外力的合力
1、瞬时加速度问题
2、从运动情况确定受力
目录
3、由受力确定运动情况
Part 01
瞬时加速度问题
一、瞬时加速度问题
1.模型特征
类别 弹力表现形式 弹力方向 能否突变
轻绳 拉力 沿绳收缩方向 能
橡皮条 拉力 沿橡皮条收缩方向 不能
轻弹簧 拉力、支持力 沿弹簧轴线方向 不能
轻杆 拉力、支持力 不确定 能
2.两个关键
3.三个步骤
(1)分析原来物体的受力情况.
(2)分析物体在弹力发生突变时的受力情况.
(3)由牛顿第二定律列方程求解.
【典例1】 (多选)如图所示,质量为m的球与弹簧Ⅰ和水平细线Ⅱ相连,Ⅰ、Ⅱ的另一端分别固定于P、Q.球静止时,Ⅰ中拉力大小为T1,Ⅱ中拉力大小为T 2,当仅剪断Ⅰ、Ⅱ中的一根的瞬间,球的加速度a应是( )
A.若剪断Ⅰ,则a=g,竖直向下
B.若剪断Ⅱ,则a=,方向水平向左
C.若剪断Ⅰ,则a=,方向沿Ⅰ的延长线
D.若剪断Ⅱ,则a=g,竖直向上
AB [绳子未断时,受力如图甲所示,
由共点力平衡条件得T 2=mg tan θ,T1= .
刚剪断弹簧Ⅰ瞬间,细线弹力突变为0,
故小球只受重力,加速度为g,竖直向下,故A正确,C错误;
刚剪断细线瞬间,弹簧弹力和重力不变,受力如图乙所示,
则F合=T1sin θ=T 2=ma,因而a==,方向水平向左,
故B正确,D错误.]
思路点拨:
①剪断水平线Ⅱ瞬间,弹簧拉力来不及恢复.
②剪断轻弹簧瞬间,轻弹簧的形变量能瞬间恢复,细线的弹力能突变为0
规律方法 两类模型的形变特点
(1)刚性绳模型(细钢丝、细绳、轻杆等):
这类形变的发生和变化过程极短,在物体的受力情况改变(如某个力消失)的瞬间,其形变可随之突变,弹力可以突变.
(2)轻弹簧模型(轻弹簧、橡皮绳、弹性绳等):
此类形变发生改变需要的时间较长,在瞬间问题中,其弹力的大小不能突变,可看成是不变的.但如果剪断轻弹簧、橡皮绳、弹性绳本身,则形变可瞬间恢复.
[课堂练习]
1.A、B两个球用轻弹簧连接,A球质量为2m,B球质量为3m,小球A由轻绳悬挂在天花板上O点,两球处于平衡状态,如图所示。现突然剪断轻绳OA,让小球下落,在剪断轻绳的瞬间,设小球A、B的加速度分别用a1和a2表示,则( )
A.a1 = g,a2 = g
B.a1 = 0,a2 = 2g
C.a1 = 2.5g,a2 = 0
D.a1 = 1.5g,a2 = 0
C 【详解】
剪断轻绳之前,对B进行分析,
弹簧处于拉伸状态,弹簧拉力大小
剪断轻绳的瞬间,分别对A、B进行分析,
根据牛顿第二定律有 ,
解得,
故选C。
[课堂练习]
2.用两根细线a、b和一个轻弹簧将两个相同的小球1和2连接并悬挂,如图所示.两小球处于静止状态,轻弹簧水平,重力加速度为g。
剪断细线b的瞬间( )
A.球1加速度大小小于g
B.球2加速度大小等于g
C.球1加速度方向竖直向下
D.球2加速度方向水平向右
A 【详解】A.设a与竖直方向的夹角为,
剪断细线b的瞬间,a绳弹力发生突变,
小球1 所受合力为
解得小球1的加速度大小为 故A正确;
B.小球1与2组成的整体,由平衡条件可得 ,
以小球2为对象,细线b对小球2的拉力大小为
剪断细线b的瞬间,弹簧c弹力不变,
小球2的合力大小为
根据牛顿第二定律可得
解得小球2的加速度大小大于,故B错误;
C.球1加速度方向与绳a垂直,故C错误;
D.球2加速度方向斜向右下方,故D错误。故选A。
[课堂练习]
3.(多选)如图所示,甲乙两图中A、B两球质量相等,图甲中A、B两球用轻质杆相连,图乙中A、B两球用轻质弹簧相连,均用细绳悬挂在天花板下处于静止状态,则在两细绳烧断的瞬间( )
A.图甲中轻杆的作用力为零
B.图甲中两球的加速度一定相等
C.图乙中两球的加速度一定相等
D.图甲中A球的加速度是图乙中A球加速度的一半
ABD [设两球质量均为m,细绳烧断的瞬间弹簧弹力不能突变,而杆的弹力会突变,所以细绳烧断瞬间,题图乙中B球所受合力仍为零,加速度为零,A球所受合力为2mg,加速度为2g;题图甲中,细绳烧断瞬间,A、B的加速度相同,设为a.以整体为研究对象,根据牛顿第二定律得2mg=2ma,得a=g,设题图甲中轻杆的作用力为T,再以B球为研究对象,由牛顿第二定律得mg+T=ma,解得T=0,即题图甲中轻杆的作用力一定为零,故A、B、D正确,C错误.]
2.分析受力情况
画受力分析图
求合
外力
求a
3.运动情况的分析
选择合适的运动学表达式
桥梁:
加速度a
1.选择研究对象
解牛顿第二定律的问题的一般步骤
F合 =ma
Part 02
从运动情况确定受力
二、从运动情况确定受力
1.基本思路:本类型问题是解决考点2中问题的逆过程,其思路如下:
2.解题步骤
(1)确定研究对象,对研究对象进行受力分析和运动过程分析,并画出受力示意图和运动草图.
(2)选择合适的运动学公式,求出物体的加速度.
(3)根据牛顿第二定律列方程,求物体所受的合外力.
(4)根据力的合成与分解的方法,由合力求出所需的力.
例题1
一列静止在站台上的火车,总质量为出发时间到了,这列火车从站台缓缓开出,1 min 20 s 后显示其速度达到. 若火车做匀加速直线运动,求火车在加速过程中的合力要多大才能满足加速的要求
例题1
一列静止在站台上的火车,总质量为出发时间到了,这列火车从站台缓缓开出,1 min 20 s 后显示其速度达到. 若火车做匀加速直线运动,求火车在加速过程中的合力要多大才能满足加速的要求
变式:若已知火车受到的阻力是车重的0.05 倍,那么这时火车所需要的牵引力应为多大?
[课堂练习]
1.如图所示的机车,质量为100 t,设它从停车场出发经225 m后速度达到15 m/s(该过程为匀加速直线运动),此时司机关闭发动机,让机车进站,机车又行驶了125 m才停在站上,设机车所受的阻力保持不变,求:
(1)机车在加速阶段和减速阶段的加速度大小;
(2)机车关闭发动机前所受的牵引力大小.
[解析] (1)设机车在加速、减速阶段的加速度大小分别为a1和a2,根据运动学公式可得2a1s1=v2,-2a2s2=
解得a1=0.5 m/s2,a2=0.9 m/s2.
(2)由牛顿第二定律得
F-f=ma1,f=ma2
解得F=1.4×105 N.
[答案] (1)0.5 m/s2 0.9 m/s2 (2)1.4×105 N
[课堂练习]
2、如图所示,截面为直角三角形的木块置于粗糙的水平地面上,其倾角θ=30°.现木块上有一质量m=1.0 kg的滑块从斜面下滑,测得滑块在0.40 s内速度增加了1.4 m/s,且知滑块滑行过程中木块处于静止状态,重力加速度g取10 m/s2,求:
(1)滑块滑行过程中受到的摩擦力大小;
(2)滑块滑行过程中木块受到地面的摩擦力大小及方向.
[解析] (1)由题意可知,滑块滑行的加速度
a== m/s2=3.5 m/s2
对滑块受力分析,如图甲所示,根据牛顿
第二定律得mg sin θ-f=ma,解得f=1.5 N。
(2)根据(1)问中的滑块受力示意图可得FN=mg cos θ.对木块受力分析,如图乙所示,根据牛顿第三定律有FN′=FN,f ′=f,根据水平方向上的平衡条件可得
f地+f′cos θ=FN′sin θ,解得f地≈3.03 N,f地为正值,说明图中标出的方向符合实际,故摩擦力方向水平向左.
[答案] (1)1.5 N (2)3.03 N 方向水平向左
甲 乙
Part 03
由受力确定运动情况
三、由受力确定运动情况
1.解题思路:
2.解题步骤
(1)确定研究对象,对研究对象进行受力分析,并画出物体的受力示意图.
(2)根据力的合成与分解,求出物体所受的合外力(包括大小和方向).
(3)根据牛顿第二定律列方程,求出物体运动的加速度.
(4)结合物体运动的初始条件,选择运动学公式,求出所需求的运动学量
——任意时刻的位移和速度,以及运动轨迹等.
课后练习1:
如图,沿倾角为θ的斜面向上拉一个质量为m的方木箱,拉力F与斜面平行,木箱与斜面的动摩擦因数为μ ,木箱沿斜面向上运动的距离为s.
(1) 画出木箱所受到的力的示意图.
(2) 写出合力的表达式.
(3) 求木箱通过距离s 所用的时间t.
教材例题2 某市交通部门规定汽车在市区某些街道的行驶速度不得超过. 一辆汽车在该水平路段紧急刹车时车轮抱死,沿直线滑行一段距离后停止.交警测得车轮在地面上滑行的轨迹长 ,从手册中查出该车轮与地面间的动摩擦因数.
试通过计算判断该汽车是否违反规定超速行驶.(取)
[课堂练习] 如图甲所示,质量为4 kg的物体放在与水平面成30°角、足够长的粗糙斜面上,物体与斜面间的动摩擦因数μ=,作用在物体上的外力与斜面平行,随时间变化的图像如图乙所示,外力作用在物体上的时间共8 s,根据所给条件(sin 30°=,cos 30°=,g取10 m/s2)问:
(1)物体所受的摩擦阻力为多大?
(2)物体在0~4 s内的加速度为多大?运动的位移为多大?
甲 乙
[解析] (1)如图,对物体进行受力分析可得:
G1=mg sin 30°=20 N
FN=G2=mg cos 30°=20 N
Ff=μFN=×20 N=20 N.
(2)由牛顿第二定律可得,0~4 s内物体的加速度为
a==5 m/s2
0~4 s内位移s1=at2=40 m.
[答案] (1)20 N (2)5 m/s2 40 m
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
