1.6 课时1 有理数的乘方 课件(共23张PPT) 2025-2026学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 1.6 课时1 有理数的乘方 课件(共23张PPT) 2025-2026学年数学沪科版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 818.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 10:23:13 | ||
图片预览






文档简介
(共23张PPT)
1.6 课时1 有理数的乘方
1.认识有理数乘方的意义,能熟练地对有理数进行乘方运算.(重点)
2.能熟练地进行有理数加、减、乘、除、乘方及简单的混合运算.(难点)
学习目标
古希腊数学家阿基米德与国王下棋,国王输了,问阿基米德要什么奖赏.阿基米德对国王说:“我只要在棋盘上第一格放一颗麦子,在第二个格子中放进前一个格子的两倍,每一个格子中都是前一个格子中麦子数量的两倍,一直将棋盘每一个格子摆满.”国王觉得很容易就可以满足他的要求,于是就同意了.但很快国王就发现,即使将国库所有的粮食都给他也不够.你们知道这是为什么吗?
新课导入
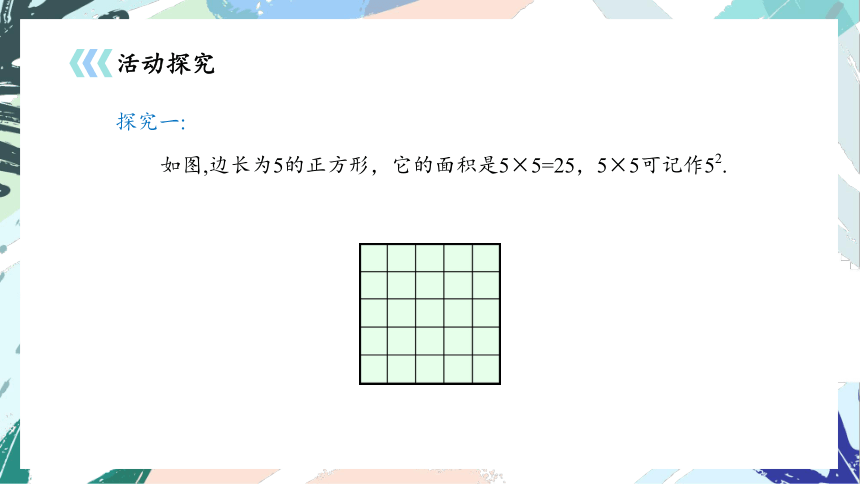
如图,边长为5的正方形,它的面积是5×5=25,5×5可记作52.
探究一:
活动探究
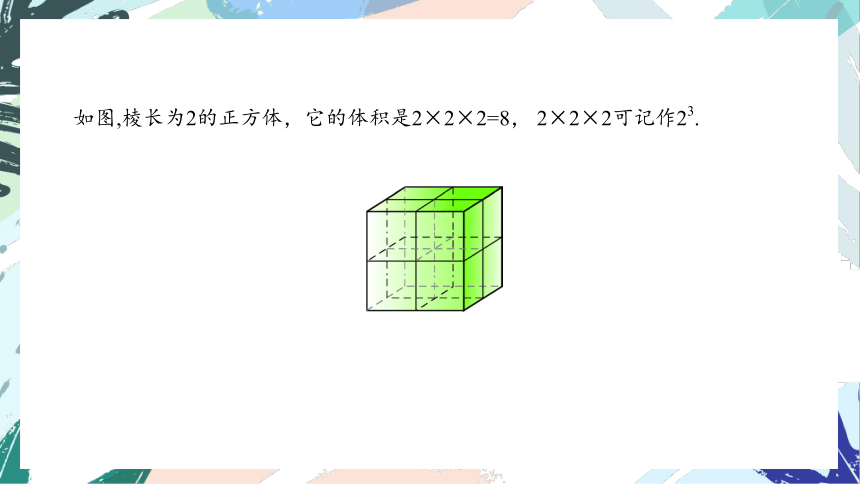
如图,棱长为2的正方体,它的体积是2×2×2=8, 2×2×2可记作23.
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
5×5× ×5
n个5
=54
=55
= 5n
a×a ×… ×a ×a
n个a
=an
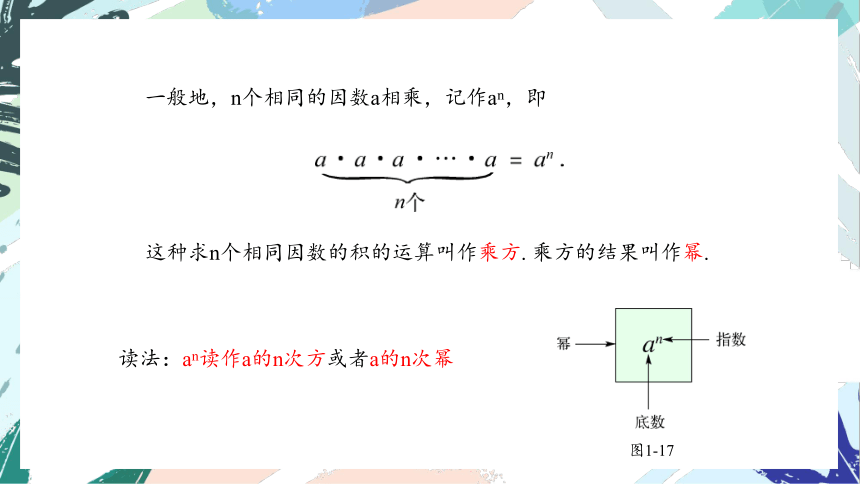
一般地,n个相同的因数a相乘,记作an,即
这种求n个相同因数的积的运算叫作乘方. 乘方的结果叫作幂.
图1-17
读法:an读作a的n次方或者a的n次幂
例如,在幂52中,底数是5,指数是2, 52读作5的2次方(或5的平方)或5的2次幂. 23读作2的3次方(或2的立方)或2的3次幂.
一个数的一次方,就是这个数本身,例如61就是6,指数1通常省略不写.
说一说:指出下列幂的底数和指数分别为什么?
(1)(3)4,
例 1 计算:
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
观察下列式子.你发现了什么?
(-3)1 = -3 31 = 3
(-3)2 = 9 32 = 9
(-3)3 = -27 33 = 27
(-3)4 = 81 34 = 81
结论:正数的任何次幂都是正数.负数的奇次幂是负数,负数的偶次幂是正数.
奇负偶正
探究二:
把下列各式写成乘方的形式,并指出底数和指数各是什么,并判断最后结果是正是负.
1.(-3.14)×(-3.14)×(-3.14)×(-3.14)×(-3.14) ×(-3.14);
2.(-5)×(-5)×(-5)×(-5)×(-5)×(-5)×(-5)
1.(-3.14)6 底数为-3.14 指数为6 最后结果为:正
2. (-5)7 底数为-5 指数为7 最后结果为:负
探究三:
1. (3和计算 结果各是多少?为什么不同?计算(-4)2与-42结果各是多少?为什么不同?你从中得到了什么提示?
答案: 16 -16
注意负数和分数的乘方,书写时要把作为底数的负数(连同负号)、分数用小括号括起来
答案:当底数大于1时, 乘方运算的结果越来越大且增长得快,当底数大于0小于1时,乘方运算的结果越来越小且减小得快
2.计算下列格式,你发现了什么规律?
1)22=_____,23=_____,24=_____
2)(0.2)2=_____,(0.2)3=_____,(0.2)4=_____
3) ()2=_____,()3=_____,()4=_____
例2:
注意:有理数的混合运算,应注意如下运算顺序:
①先算乘方,再算乘除,最后算加减;
②同级运算,按照从左至右的顺序进行;
③如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
答案 (1)原式
(2)原式
练一练
1.计算:
(1)9-(-18)÷|-3|+(-3).
(2)-4+ ×(-3)- ÷4 .
(3)-27× +|-4|÷(-2).
1. (-2)2+22= ( )
A.0 B.2 C.4 D.8
D
解析 (-2)2+22=4+4=8.故选D.
当堂检测
2.(2024安徽滁州天长期中)下列各组数:①-(-3)和-|-3|;②(-2)4和-24;③(-2)3和(-3)2;④(-2)3和-23.其中互为相反数的有 ( )
A.①② B.①②③ C.①②④ D.②
A
解析 ①-(-3)=3,-|-3|=-3,互为相反数;②(-2)4=16,-24=-16,互为相反数;③(-2)3=-8,(-3)2=9,不互为相反数;④(-2)3=-8,-23=-8,相
等,不互为相反数.所以互为相反数的有①②.故选A.
3.若a,b均表示有理数,则下列结论错误的是 ( )
A.若a2+b2=0,则a=b=0
B.若a3+b3=0,则a=b=0
C.若|a|+|b|=0,则a=b=0
D.若|a|+b2=0,则a=b=0
B
解析 非负数之和为0的数都是0,a2,|a|,b2和|b|是非负数,而a3和b3不是非负数,由a3+b3=0不能推理出a=b=0.故选B.
4.(易错题)(2023安徽芜湖期中)下列各数:-(+2),-32, ,- ,-(-1)2 015,-|-3|.其中负数的个数是 ( )
A.2 B.3 C.4 D.5
C
易错点 计算 和- 时,易忽视运算顺序导致符号判断错误.
5.(2023安徽合肥高新区月考)随着人们生活水平的提高,家用轿车越来越多地进入家庭.小亮家中买了一辆小轿车,他连续记录了7天每天行驶的路程(如表),以50 km为标
准,多于50 km的记为“+”,不足50 km的记为“-”,刚好50km的记为“0”.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程(km) -7 -12 -13 0 -17 +40 +9
(1)请求出这7天平均每天行驶的路程.
(2)若该汽车平均每百千米耗油9升,汽油价格为8.8元/升,计算小亮家这7天的汽油费用.
解析 (1)50×7+(-7-12-13+0-17+40+9)
=350+[-(7+12+13+17)+(40+9)]
=350+(-49+49)
=350(km),
350÷7=50(km).
答:这7天平均每天行驶的路程为50 km.
(2)350÷100×9×8.8=3.5×9×8.8=277.2(元).
答:小亮家这7天的汽油费用为277.2元.
1.有理数乘方的意义.
n个相同因数的积的运算叫做乘方.乘方的结果叫做幂,相同的因数叫做底数,相同因数的个数叫做指数(指数1通常不写).
2.有理数乘方运算的符号法则.
3.含乘方的混合运算.
负数的奇次幂是负数,负数的偶次幂是正数.正数的任何次幂都是正数,0的任何正整数次幂都是0.
先算乘方,再算乘除,最后算加减,如有括号,先进行括号里的运算.
课堂总结
1.6 课时1 有理数的乘方
1.认识有理数乘方的意义,能熟练地对有理数进行乘方运算.(重点)
2.能熟练地进行有理数加、减、乘、除、乘方及简单的混合运算.(难点)
学习目标
古希腊数学家阿基米德与国王下棋,国王输了,问阿基米德要什么奖赏.阿基米德对国王说:“我只要在棋盘上第一格放一颗麦子,在第二个格子中放进前一个格子的两倍,每一个格子中都是前一个格子中麦子数量的两倍,一直将棋盘每一个格子摆满.”国王觉得很容易就可以满足他的要求,于是就同意了.但很快国王就发现,即使将国库所有的粮食都给他也不够.你们知道这是为什么吗?
新课导入
如图,边长为5的正方形,它的面积是5×5=25,5×5可记作52.
探究一:
活动探究
如图,棱长为2的正方体,它的体积是2×2×2=8, 2×2×2可记作23.
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
5×5× ×5
n个5
=54
=55
= 5n
a×a ×… ×a ×a
n个a
=an
一般地,n个相同的因数a相乘,记作an,即
这种求n个相同因数的积的运算叫作乘方. 乘方的结果叫作幂.
图1-17
读法:an读作a的n次方或者a的n次幂
例如,在幂52中,底数是5,指数是2, 52读作5的2次方(或5的平方)或5的2次幂. 23读作2的3次方(或2的立方)或2的3次幂.
一个数的一次方,就是这个数本身,例如61就是6,指数1通常省略不写.
说一说:指出下列幂的底数和指数分别为什么?
(1)(3)4,
例 1 计算:
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
观察下列式子.你发现了什么?
(-3)1 = -3 31 = 3
(-3)2 = 9 32 = 9
(-3)3 = -27 33 = 27
(-3)4 = 81 34 = 81
结论:正数的任何次幂都是正数.负数的奇次幂是负数,负数的偶次幂是正数.
奇负偶正
探究二:
把下列各式写成乘方的形式,并指出底数和指数各是什么,并判断最后结果是正是负.
1.(-3.14)×(-3.14)×(-3.14)×(-3.14)×(-3.14) ×(-3.14);
2.(-5)×(-5)×(-5)×(-5)×(-5)×(-5)×(-5)
1.(-3.14)6 底数为-3.14 指数为6 最后结果为:正
2. (-5)7 底数为-5 指数为7 最后结果为:负
探究三:
1. (3和计算 结果各是多少?为什么不同?计算(-4)2与-42结果各是多少?为什么不同?你从中得到了什么提示?
答案: 16 -16
注意负数和分数的乘方,书写时要把作为底数的负数(连同负号)、分数用小括号括起来
答案:当底数大于1时, 乘方运算的结果越来越大且增长得快,当底数大于0小于1时,乘方运算的结果越来越小且减小得快
2.计算下列格式,你发现了什么规律?
1)22=_____,23=_____,24=_____
2)(0.2)2=_____,(0.2)3=_____,(0.2)4=_____
3) ()2=_____,()3=_____,()4=_____
例2:
注意:有理数的混合运算,应注意如下运算顺序:
①先算乘方,再算乘除,最后算加减;
②同级运算,按照从左至右的顺序进行;
③如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
答案 (1)原式
(2)原式
练一练
1.计算:
(1)9-(-18)÷|-3|+(-3).
(2)-4+ ×(-3)- ÷4 .
(3)-27× +|-4|÷(-2).
1. (-2)2+22= ( )
A.0 B.2 C.4 D.8
D
解析 (-2)2+22=4+4=8.故选D.
当堂检测
2.(2024安徽滁州天长期中)下列各组数:①-(-3)和-|-3|;②(-2)4和-24;③(-2)3和(-3)2;④(-2)3和-23.其中互为相反数的有 ( )
A.①② B.①②③ C.①②④ D.②
A
解析 ①-(-3)=3,-|-3|=-3,互为相反数;②(-2)4=16,-24=-16,互为相反数;③(-2)3=-8,(-3)2=9,不互为相反数;④(-2)3=-8,-23=-8,相
等,不互为相反数.所以互为相反数的有①②.故选A.
3.若a,b均表示有理数,则下列结论错误的是 ( )
A.若a2+b2=0,则a=b=0
B.若a3+b3=0,则a=b=0
C.若|a|+|b|=0,则a=b=0
D.若|a|+b2=0,则a=b=0
B
解析 非负数之和为0的数都是0,a2,|a|,b2和|b|是非负数,而a3和b3不是非负数,由a3+b3=0不能推理出a=b=0.故选B.
4.(易错题)(2023安徽芜湖期中)下列各数:-(+2),-32, ,- ,-(-1)2 015,-|-3|.其中负数的个数是 ( )
A.2 B.3 C.4 D.5
C
易错点 计算 和- 时,易忽视运算顺序导致符号判断错误.
5.(2023安徽合肥高新区月考)随着人们生活水平的提高,家用轿车越来越多地进入家庭.小亮家中买了一辆小轿车,他连续记录了7天每天行驶的路程(如表),以50 km为标
准,多于50 km的记为“+”,不足50 km的记为“-”,刚好50km的记为“0”.
第一天 第二天 第三天 第四天 第五天 第六天 第七天
路程(km) -7 -12 -13 0 -17 +40 +9
(1)请求出这7天平均每天行驶的路程.
(2)若该汽车平均每百千米耗油9升,汽油价格为8.8元/升,计算小亮家这7天的汽油费用.
解析 (1)50×7+(-7-12-13+0-17+40+9)
=350+[-(7+12+13+17)+(40+9)]
=350+(-49+49)
=350(km),
350÷7=50(km).
答:这7天平均每天行驶的路程为50 km.
(2)350÷100×9×8.8=3.5×9×8.8=277.2(元).
答:小亮家这7天的汽油费用为277.2元.
1.有理数乘方的意义.
n个相同因数的积的运算叫做乘方.乘方的结果叫做幂,相同的因数叫做底数,相同因数的个数叫做指数(指数1通常不写).
2.有理数乘方运算的符号法则.
3.含乘方的混合运算.
负数的奇次幂是负数,负数的偶次幂是正数.正数的任何次幂都是正数,0的任何正整数次幂都是0.
先算乘方,再算乘除,最后算加减,如有括号,先进行括号里的运算.
课堂总结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
