1.2 课时2 相反数 课件(共19张PPT) 2025-2026学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 1.2 课时2 相反数 课件(共19张PPT) 2025-2026学年数学沪科版(2024)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 267.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第1章 有理数
1.2 课时2 相反数
1.理解相反数的概念,会求一个有理数的相反数.
2. 表示互为相反数的两个点在数轴上的位置关系,根据相反数的概念化简多重符号.
4
0
1
2
1
2
3
3
4
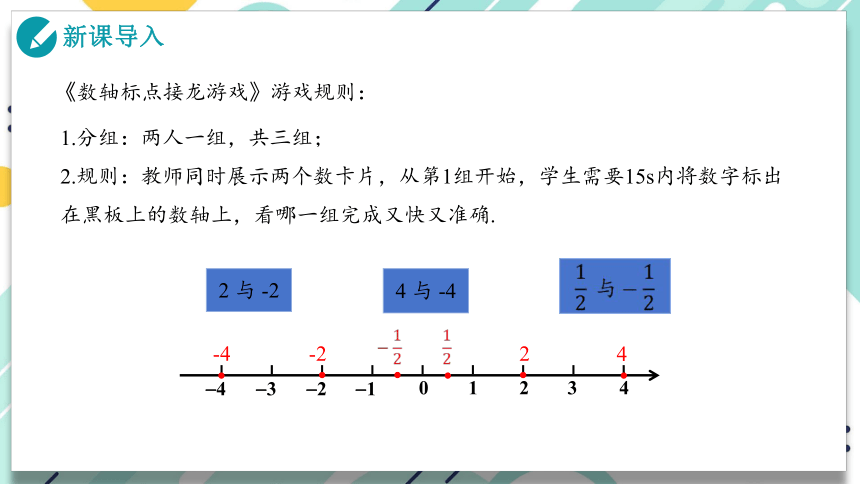
《数轴标点接龙游戏》游戏规则:
1.分组:两人一组,共三组;
2.规则:教师同时展示两个数卡片,从第1组开始,学生需要15s内将数字标出在黑板上的数轴上,看哪一组完成又快又准确.
2 与 -2
4 与 -4
-4
-2
2
4
各有什么相同点和不同点?在数轴上画出表示它们的点,说说它们的位置有什么关系?
各有什么相同点和不同点?
数字相同
符号不同
在数轴上画出表示它们的点,说说它们的位置有什么关系?
4
0
1
2
1
2
3
3
4
-4
-2
2
4
到原点的距离相等
在原点两侧
我们称只有符号不同的两个数互为相反数.
这就是说,其中一个数是另一个数的相反数,如2与 2互为相反数,即2的相反数是 2, 2的相反数是2.
都只有符号不同.
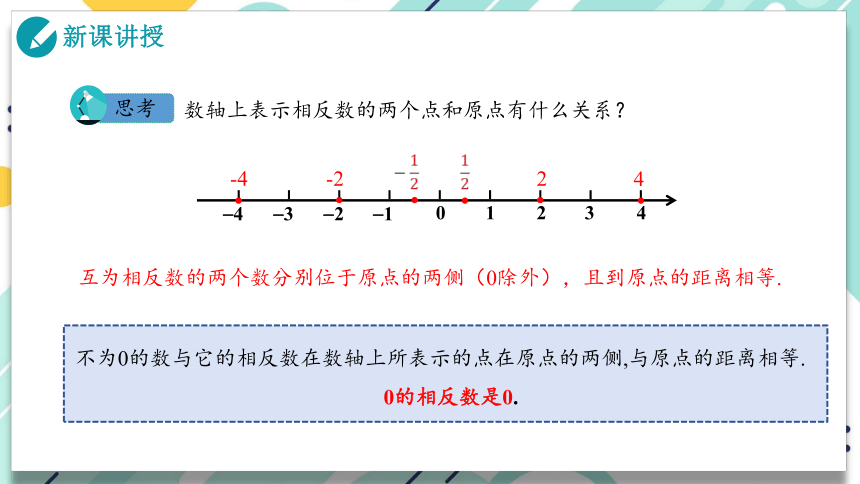
思考
数轴上表示相反数的两个点和原点有什么关系?
4
0
1
2
1
2
3
3
4
-4
-2
2
4
不为0的数与它的相反数在数轴上所表示的点在原点的两侧,与原点的距离相等.
0的相反数是0.
互为相反数的两个数分别位于原点的两侧(0除外),且到原点的距离相等.
练一练
1.判断题
(1)-6 是 6 的相反数( );
(2)-5 是相反数( );
(3) 与 互为相反数( );
(4)-1 和 1 互为相反数( );
(5)相反数等于它本身的数只有 0 ﹙ ﹚;
(6)符号不同的两个数互为相反数﹙ ﹚.
×
√
×
√
√
×
2.写出下列各数.
(1)-3 的相反数; (2)0 的相反数;
(3)相反数是 的数; (4)相反数是-0.5的数.
解:(1)-3的相反数是3;
(2)0的相反数是0;
(3)相反数是 的数是 ;
(4)相反数是-0.5的数是0.5.
例1.写出下列各数的相反数:
解:
3的相反数是-3,
-7的相反数是7,
-2.1的相反数是2.1.
0 的相反数是0,
20的相反数是-20.
的相反数是-
的相反数是
探索:多重符号的化简
a是表示任意的有理数,a相反数是什么?
a 的相反数是-a
在任意一个数前面添上“-”号,所得的数就是原数的相反数,如-(+3)=-3,-(-3)=3,-0=0.
数a的相反数是-a.这里a表示任意一个数,它可以是正数、负数或者0.
-a不一定表示一个负数.
练一练
化简下列各数:
(1)(+10); (2)+(0.15); (3)+(+3);
(4)(12); (5)+[(1.1)] ; (6)[+(7)].
解:(1)(+10)=10; (2)+(0.15)=0.15; (3)+(+3)=3;
(4)(12)=12; (5)+[(1.1)]=+(+1.1)=1.1; (6)[+(7)]=(7)=7.
拓展提升
(1) 当 +5 前面有7个负号,化简后结果是多少?
(2) 当 -5 前面有100个负号,化简后结果是多少?
解: (1) -5 (2) -5
你能总结出什么规律?
对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.
多重符号化简规律:
负号是偶数数个,结果为正数;
负号是奇数数个,结果为负数.
1.下列说法中,正确的是 ( )
A. 正数与负数互为相反数
B. 符号不同的两个数互为相反数
C. 数轴上原点两侧的两个点所表示的数互为相反数
D. 任何一个有理数都有相反数
D
2.填空题
2.3是____的相反数,____的相反数是0.3.
6的相反数是____;-a的相反数是_____.
2.3
-0.3
-6
a
3.我们知道-a表示a的相反数,同理-(a-3)表示数(a-3) 的相反数.请根据相反数的意义,解决问题:若-[-(a-3)]和-[-(-8) ]互为相反数,求a的值.
a-3=8
a=11
所以a的值是11.
解:-[-(a-3) ]=a-3,-[-(-8)]=-8,
几何意义:两个互为相反数的数在数轴上所表示的点在 原点的两旁,且与原点的距离相等
相反数
多重符号化简规律:
负号是偶数数个,结果为正数;
负号是奇数数个,结果为负数.
概念:只有符号不同的两个数互为相反数.
数a的相反数是-a;0的相反数是0
第1章 有理数
1.2 课时2 相反数
1.理解相反数的概念,会求一个有理数的相反数.
2. 表示互为相反数的两个点在数轴上的位置关系,根据相反数的概念化简多重符号.
4
0
1
2
1
2
3
3
4
《数轴标点接龙游戏》游戏规则:
1.分组:两人一组,共三组;
2.规则:教师同时展示两个数卡片,从第1组开始,学生需要15s内将数字标出在黑板上的数轴上,看哪一组完成又快又准确.
2 与 -2
4 与 -4
-4
-2
2
4
各有什么相同点和不同点?在数轴上画出表示它们的点,说说它们的位置有什么关系?
各有什么相同点和不同点?
数字相同
符号不同
在数轴上画出表示它们的点,说说它们的位置有什么关系?
4
0
1
2
1
2
3
3
4
-4
-2
2
4
到原点的距离相等
在原点两侧
我们称只有符号不同的两个数互为相反数.
这就是说,其中一个数是另一个数的相反数,如2与 2互为相反数,即2的相反数是 2, 2的相反数是2.
都只有符号不同.
思考
数轴上表示相反数的两个点和原点有什么关系?
4
0
1
2
1
2
3
3
4
-4
-2
2
4
不为0的数与它的相反数在数轴上所表示的点在原点的两侧,与原点的距离相等.
0的相反数是0.
互为相反数的两个数分别位于原点的两侧(0除外),且到原点的距离相等.
练一练
1.判断题
(1)-6 是 6 的相反数( );
(2)-5 是相反数( );
(3) 与 互为相反数( );
(4)-1 和 1 互为相反数( );
(5)相反数等于它本身的数只有 0 ﹙ ﹚;
(6)符号不同的两个数互为相反数﹙ ﹚.
×
√
×
√
√
×
2.写出下列各数.
(1)-3 的相反数; (2)0 的相反数;
(3)相反数是 的数; (4)相反数是-0.5的数.
解:(1)-3的相反数是3;
(2)0的相反数是0;
(3)相反数是 的数是 ;
(4)相反数是-0.5的数是0.5.
例1.写出下列各数的相反数:
解:
3的相反数是-3,
-7的相反数是7,
-2.1的相反数是2.1.
0 的相反数是0,
20的相反数是-20.
的相反数是-
的相反数是
探索:多重符号的化简
a是表示任意的有理数,a相反数是什么?
a 的相反数是-a
在任意一个数前面添上“-”号,所得的数就是原数的相反数,如-(+3)=-3,-(-3)=3,-0=0.
数a的相反数是-a.这里a表示任意一个数,它可以是正数、负数或者0.
-a不一定表示一个负数.
练一练
化简下列各数:
(1)(+10); (2)+(0.15); (3)+(+3);
(4)(12); (5)+[(1.1)] ; (6)[+(7)].
解:(1)(+10)=10; (2)+(0.15)=0.15; (3)+(+3)=3;
(4)(12)=12; (5)+[(1.1)]=+(+1.1)=1.1; (6)[+(7)]=(7)=7.
拓展提升
(1) 当 +5 前面有7个负号,化简后结果是多少?
(2) 当 -5 前面有100个负号,化简后结果是多少?
解: (1) -5 (2) -5
你能总结出什么规律?
对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.
多重符号化简规律:
负号是偶数数个,结果为正数;
负号是奇数数个,结果为负数.
1.下列说法中,正确的是 ( )
A. 正数与负数互为相反数
B. 符号不同的两个数互为相反数
C. 数轴上原点两侧的两个点所表示的数互为相反数
D. 任何一个有理数都有相反数
D
2.填空题
2.3是____的相反数,____的相反数是0.3.
6的相反数是____;-a的相反数是_____.
2.3
-0.3
-6
a
3.我们知道-a表示a的相反数,同理-(a-3)表示数(a-3) 的相反数.请根据相反数的意义,解决问题:若-[-(a-3)]和-[-(-8) ]互为相反数,求a的值.
a-3=8
a=11
所以a的值是11.
解:-[-(a-3) ]=a-3,-[-(-8)]=-8,
几何意义:两个互为相反数的数在数轴上所表示的点在 原点的两旁,且与原点的距离相等
相反数
多重符号化简规律:
负号是偶数数个,结果为正数;
负号是奇数数个,结果为负数.
概念:只有符号不同的两个数互为相反数.
数a的相反数是-a;0的相反数是0
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
