粤教版高中物理选择性必修第一册第二章机械振动2.2简谐运动的描述教学课件(共20张ppt)
文档属性
| 名称 | 粤教版高中物理选择性必修第一册第二章机械振动2.2简谐运动的描述教学课件(共20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 22:17:03 | ||
图片预览




文档简介
(共20张PPT)
第二章 机械振动
2 简谐运动的描述
学习目标
1.理解振幅、周期和频率的物理意义,了解相位、初相、相位差的概念.(重点)
2.理解周期和频率的关系.
3.掌握用公式描述简谐运动的方法.(难点)
复习回顾
1、什么是简谐振动?
2、什么是简谐运动?
物体(或者物体的一部分)在某一中心位置(平衡位置)两侧所做的往复运动叫做机械振动,简称振动。
振子一直在平衡位置附近振动,每个全振动中偏离平衡位置的最大距离和需要的时间都不变,振子的位移—时间函数为正弦或者余弦函数,我们把具有这种特征的运动叫做简谐运动。
一、简谐运动的函数描述
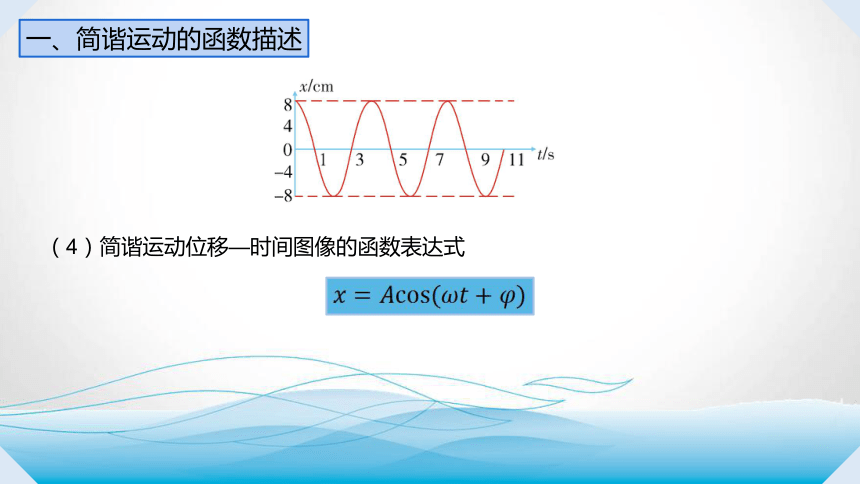
(1)简谐运动的位移—时间图象反映的是质点偏离平衡位置的位移随时间变化的规律,简谐运动的图象并不是质点的运动轨迹,运动轨迹的长度也不是正弦或余弦图线拉开后的长度.
(2)在x t图象上,质点在某时刻的位移,即为此时刻对应的纵坐标.
(3)质点在某段时间内的路程(轨迹的长度),需结合振动质点的实际运动轨迹进行计算.
一、简谐运动的函数描述
(4)简谐运动位移—时间图像的函数表达式
一、简谐运动的函数描述
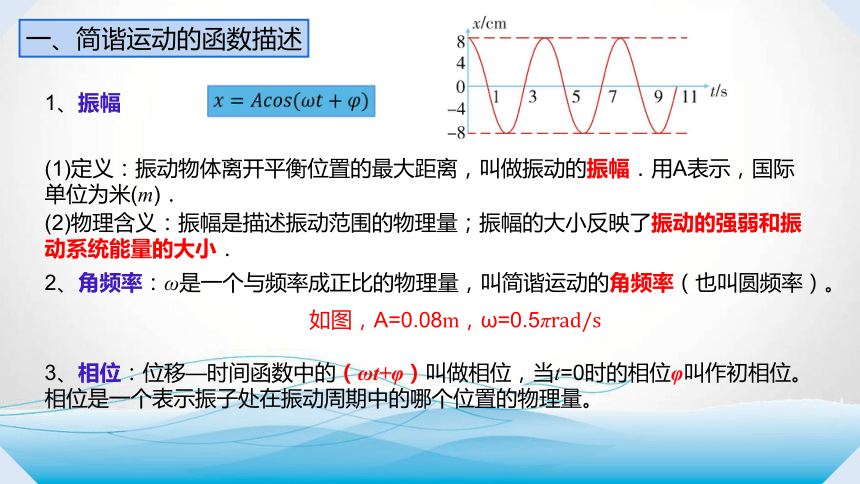
1、振幅
(1)定义:振动物体离开平衡位置的最大距离,叫做振动的振幅.用A表示,国际单位为米(m).
(2)物理含义:振幅是描述振动范围的物理量;振幅的大小反映了振动的强弱和振动系统能量的大小.
2、角频率:ω是一个与频率成正比的物理量,叫简谐运动的角频率(也叫圆频率)。
如图,A=0.08m,ω=0.5πrad/s
3、相位:位移—时间函数中的(ωt+φ)叫做相位,当t=0时的相位φ叫作初相位。
相位是一个表示振子处在振动周期中的哪个位置的物理量。
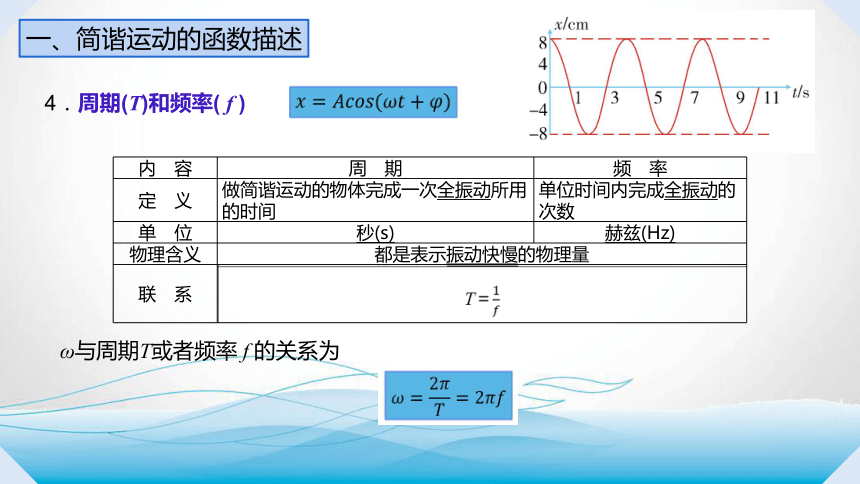
内 容 周 期 频 率
定 义 做简谐运动的物体完成一次全振动所用的时间 单位时间内完成全振动的次数
单 位 秒(s) 赫兹(Hz)
物理含义 都是表示振动快慢的物理量
联 系
4.周期(T)和频率( f )
一、简谐运动的函数描述
ω与周期T或者频率 f 的关系为
一、简谐运动的函数描述
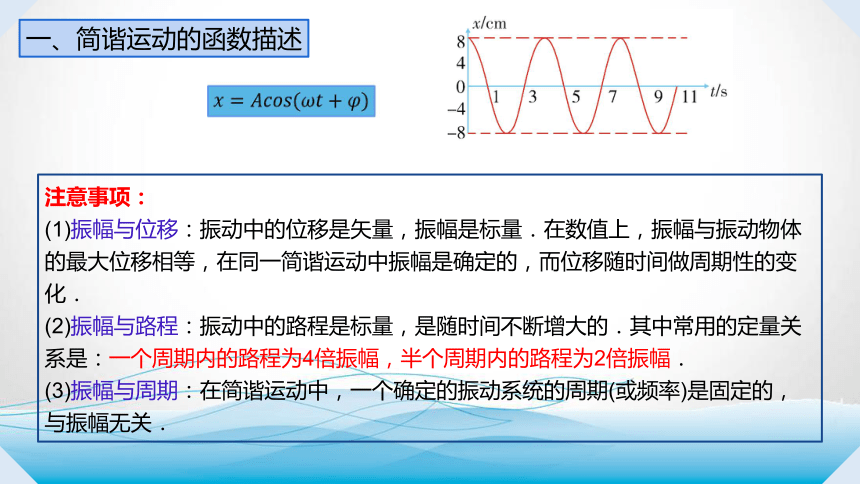
注意事项:
(1)振幅与位移:振动中的位移是矢量,振幅是标量.在数值上,振幅与振动物体的最大位移相等,在同一简谐运动中振幅是确定的,而位移随时间做周期性的变化.
(2)振幅与路程:振动中的路程是标量,是随时间不断增大的.其中常用的定量关系是:一个周期内的路程为4倍振幅,半个周期内的路程为2倍振幅.
(3)振幅与周期:在简谐运动中,一个确定的振动系统的周期(或频率)是固定的,与振幅无关.
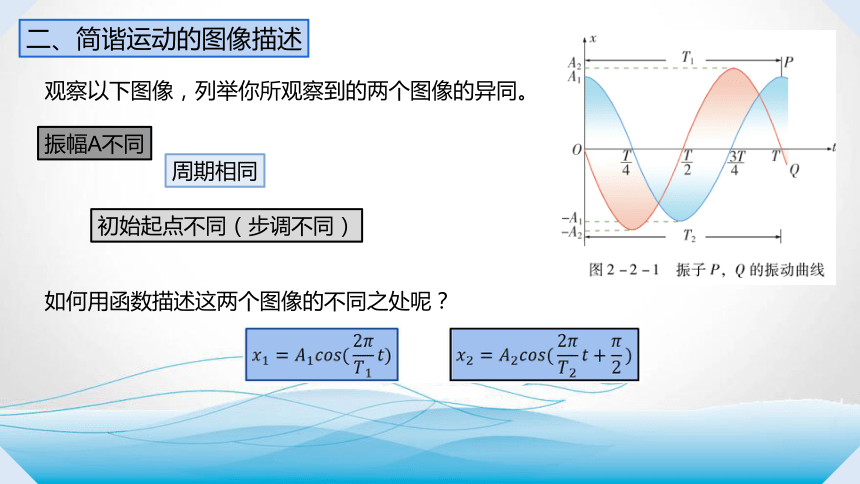
二、简谐运动的图像描述
观察以下图像,列举你所观察到的两个图像的异同。
振幅A不同
周期相同
初始起点不同(步调不同)
如何用函数描述这两个图像的不同之处呢?
二、简谐运动的图像描述
(1)两个函数的相位是不同的,对于频率相同、相位不同的振子,我们通过对比它们的相位差来比较它们的振动先后的关系。若相位差用Δφ表示,则
Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1
相位是一个相对概念,与所取的时间零点有关。两个振动的相位差是一个绝对的概念,表示两个频率相同的简谐运动的振动先后的关系。
①若△φ=φ2-φ1>0 ,振动2的相位比1超前△φ;
②若△φ=φ2-φ1<0,振动2的相位比1落后△φ。
课堂小结
位 移
振 幅
初 相
相 位
圆频率
周 期
课堂练习
1.判一判
(1)简谐运动的振幅大,振动的周期一定大。( )
(2)振幅就是振子的最大位移。( )
(3)振子从离开某位置到重新回到该位置的过程为一次全振动过程。( )
(4)两个振动物体相位相同,则其振动步调相反。( )
(5)简谐运动的表达式x=Asin(ωt+φ)中,ωt+φ的单位是弧度。( )
(6)简谐运动的表达式x=Asin(ωt+φ)中,ω表示振动的快慢,ω越大,振动的周期越小。( )
√
√
×
×
×
×
课堂练习
课堂练习
BCD
课堂练习
B
课堂练习
AC
课堂练习
CD
课堂练习
课堂练习
课堂练习
第二章 机械振动
2 简谐运动的描述
学习目标
1.理解振幅、周期和频率的物理意义,了解相位、初相、相位差的概念.(重点)
2.理解周期和频率的关系.
3.掌握用公式描述简谐运动的方法.(难点)
复习回顾
1、什么是简谐振动?
2、什么是简谐运动?
物体(或者物体的一部分)在某一中心位置(平衡位置)两侧所做的往复运动叫做机械振动,简称振动。
振子一直在平衡位置附近振动,每个全振动中偏离平衡位置的最大距离和需要的时间都不变,振子的位移—时间函数为正弦或者余弦函数,我们把具有这种特征的运动叫做简谐运动。
一、简谐运动的函数描述
(1)简谐运动的位移—时间图象反映的是质点偏离平衡位置的位移随时间变化的规律,简谐运动的图象并不是质点的运动轨迹,运动轨迹的长度也不是正弦或余弦图线拉开后的长度.
(2)在x t图象上,质点在某时刻的位移,即为此时刻对应的纵坐标.
(3)质点在某段时间内的路程(轨迹的长度),需结合振动质点的实际运动轨迹进行计算.
一、简谐运动的函数描述
(4)简谐运动位移—时间图像的函数表达式
一、简谐运动的函数描述
1、振幅
(1)定义:振动物体离开平衡位置的最大距离,叫做振动的振幅.用A表示,国际单位为米(m).
(2)物理含义:振幅是描述振动范围的物理量;振幅的大小反映了振动的强弱和振动系统能量的大小.
2、角频率:ω是一个与频率成正比的物理量,叫简谐运动的角频率(也叫圆频率)。
如图,A=0.08m,ω=0.5πrad/s
3、相位:位移—时间函数中的(ωt+φ)叫做相位,当t=0时的相位φ叫作初相位。
相位是一个表示振子处在振动周期中的哪个位置的物理量。
内 容 周 期 频 率
定 义 做简谐运动的物体完成一次全振动所用的时间 单位时间内完成全振动的次数
单 位 秒(s) 赫兹(Hz)
物理含义 都是表示振动快慢的物理量
联 系
4.周期(T)和频率( f )
一、简谐运动的函数描述
ω与周期T或者频率 f 的关系为
一、简谐运动的函数描述
注意事项:
(1)振幅与位移:振动中的位移是矢量,振幅是标量.在数值上,振幅与振动物体的最大位移相等,在同一简谐运动中振幅是确定的,而位移随时间做周期性的变化.
(2)振幅与路程:振动中的路程是标量,是随时间不断增大的.其中常用的定量关系是:一个周期内的路程为4倍振幅,半个周期内的路程为2倍振幅.
(3)振幅与周期:在简谐运动中,一个确定的振动系统的周期(或频率)是固定的,与振幅无关.
二、简谐运动的图像描述
观察以下图像,列举你所观察到的两个图像的异同。
振幅A不同
周期相同
初始起点不同(步调不同)
如何用函数描述这两个图像的不同之处呢?
二、简谐运动的图像描述
(1)两个函数的相位是不同的,对于频率相同、相位不同的振子,我们通过对比它们的相位差来比较它们的振动先后的关系。若相位差用Δφ表示,则
Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1
相位是一个相对概念,与所取的时间零点有关。两个振动的相位差是一个绝对的概念,表示两个频率相同的简谐运动的振动先后的关系。
①若△φ=φ2-φ1>0 ,振动2的相位比1超前△φ;
②若△φ=φ2-φ1<0,振动2的相位比1落后△φ。
课堂小结
位 移
振 幅
初 相
相 位
圆频率
周 期
课堂练习
1.判一判
(1)简谐运动的振幅大,振动的周期一定大。( )
(2)振幅就是振子的最大位移。( )
(3)振子从离开某位置到重新回到该位置的过程为一次全振动过程。( )
(4)两个振动物体相位相同,则其振动步调相反。( )
(5)简谐运动的表达式x=Asin(ωt+φ)中,ωt+φ的单位是弧度。( )
(6)简谐运动的表达式x=Asin(ωt+φ)中,ω表示振动的快慢,ω越大,振动的周期越小。( )
√
√
×
×
×
×
课堂练习
课堂练习
BCD
课堂练习
B
课堂练习
AC
课堂练习
CD
课堂练习
课堂练习
课堂练习
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
