5.1.4 用样本估计总体(教学课件)__高中数学人教B版(2019)必修第二册(共31张PPT)
文档属性
| 名称 | 5.1.4 用样本估计总体(教学课件)__高中数学人教B版(2019)必修第二册(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 07:15:59 | ||
图片预览








文档简介
(共29张PPT)
人教B版(2019)必修第二册
第五章 统计与概率
5.1.4 用样本估计总体
学习目标
会用样本的数字特征估计总体的数字特征
01
能用样本的分布来估计总体的分布
02
探索新知
以下是某高校高一年级 98 位学生的身高(单位:cm):
已知这组数的总体平均数为 163.5,总体方差为 56.3.
161 168 166 168 152 152 163 164 170 167 143 166 153 165
168 167 163 157 160 159 153 169 172 175 165 161 158 172
147 164 171 149 158 155 169 150 173 170 162 157 152 180
178 158 162 164 172 165 165 155 163 178 159 168 161 151
168 168 165 158 162 165 163 166 174 163 163 175 165 160
161 177 163 170 155 156 161 169 167 151 156 158 165 179
161 176 162 168 153 169 155 165 163 166 172 160 173 164
用简单随机抽样的方法从总体中抽取容量为 10 的样本 3 次,分别计算样本平均数与样本方差,并与总体对应的值进行比较.
情境与问题
探索新知
用简单随机抽样样本的数字特征估计总体的数字特征
一般情况下,如果样本的容量恰当,抽样方法又合理的话,样本的特征能够反映总体的特征.特别地,样本平均数(也称为样本均值)、方差(也称为样本方差)与总体对应的值相差不会太大.
例如,上述数据中,如果用简单随机抽样抽得的序号分别为 90,35,63,68,66,9,30,56,50,49,则对应的样本为:169,169,163,175,163,170,164,151,155,165,容易算出,样本均值为 164.4,样本方差为 45.84,它们与总体对应的值差别都不大.
这就说明 , 在容许一定误差存在的前提下 , 可以用样本的数字特征去估计总体的数字特征 , 这样就能节省人力和物力等.
探索新知
用简单随机抽样样本的数字特征估计总体的数字特征
另外,有时候总体的数字特征不可能获得,比如质监部门想知道市场上节能灯的平均使用寿命,不可能把所有节能灯都拿来检测,此时只能用样本的数字特征去估计总体的数字特征.
一般来说,在估计总体的数字特征时,只需直接算出样本对应的数字特征即可.
需要强调的是,估计一般是有误差的. 例如,如果总体平均数记为 ,样本均值记为 ,一般来说,,, 都有可能. 但是,大数定律可以保证,当样本的容量越来越大时,估计的误差很小的可能性将越来越大.
情境与问题
在考察某中学的学生的平均身高时,如果采用分层抽样的方法,得到了男生身高的平均数为 170,方差为 16;女生身高的平均数为 165,方差为 25.
(1)如果没有其它信息,怎样估计总体的平均数与方差?
(2)如果知道抽取的样本中,男生有 20 人,女生有 15 人,怎么估计总体的平均数与方差?
方法一:作为估计来说,我们可以选择男生(或女生)样本的平均数与方差作为总体对应值的估计,但这样的选择没有充分利用已知的数据,显然不够好.
探索新知
情境与问题
探索新知
在考察某中学的学生的平均身高时,如果采用分层抽样的方法,得到了男生身高的平均数为 170,方差为 16;女生身高的平均数为 165,方差为 25.
(1)如果没有其它信息,怎样估计总体的平均数与方差?
(2)如果知道抽取的样本中,男生有 20 人,女生有 15 人,怎么估计总体的平均数与方差?
方法二:取每一层样本数字特征的算术平均值作为总体的估计,即估
计总体平均数为 ,
类似地,总体方差可估计为 .
探索新知
但第二种估计方法也还不太理想,因为对于分层抽样来说,每一层所抽取的个体数目一般来说是不相等的,简单的求数字特征的算术平均值体现不出这一点.
怎样才能体现这一点呢?尤其是,当我们把各层中得到的个体放在一起作为一个样本时,样本均值与样本方差该如何计算呢?
此时,当然可以把各层数据集中在一起来重新计算,但也可以去考虑整个样本的数字特征与每一层的数字特征之间的关系来实现,后者在大数据时代的并行计算中经常使用.
探索新知
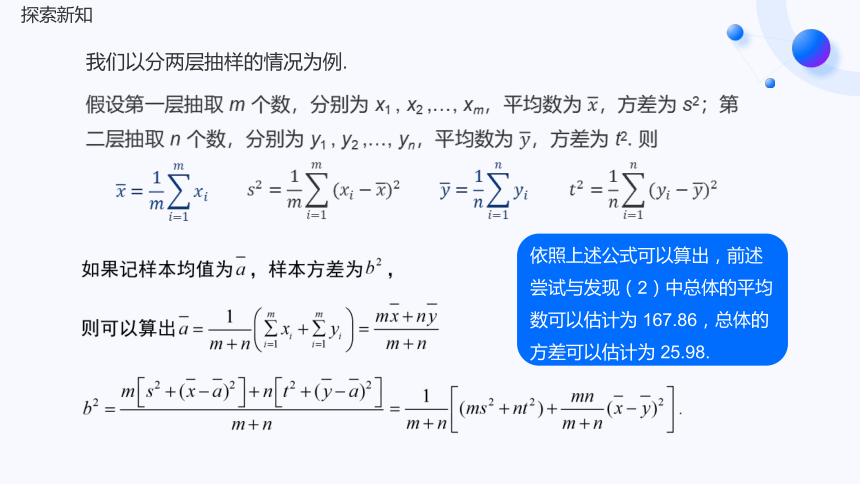
我们以分两层抽样的情况为例.
假设第一层抽取 m 个数,分别为 x1 , x2 ,…, xm,平均数为 ,方差为 s2;第二层抽取 n 个数,分别为 y1 , y2 ,…, yn,平均数为 ,方差为 t2. 则
依照上述公式可以算出,前述尝试与发现(2)中总体的平均数可以估计为 167.86,总体的方差可以估计为 25.98.
探索新知
分层抽样的均值与方差
一般地,设样本中不同层的平均数分别为 ,…,,方差分别为 ,…,,,相应的权重分别为 ,则
平均数:
方差:
情境与问题
探索新知
通过对某中学 1 257 名高一学生期中考试的数学成绩(具体数据参见这一小节的附录)进行整理,可以得到如下数据,并由此可作出频率分布直方图和折线图,如图所示.
从附录的数据中抽取容量为 100 的样本,整理类似的表格,并制作频率分布直方图.
探索新知
同前面一样,如果样本的容量恰当,抽样方法又合理的话,样本的分布与总体分布会差不多.特别地,每一组的频率与总体对应的频率相差不会太大.
如果从上述尝试与发现中提到的数据中,抽取两个容量为 100 的样本(分别记为样本 A,样本 B,具体数据参见这一小节的附录),则可以得到如下频数、频率对应表:
探索新知
它们的频率分布直方图分别如图 (1) (2) 所示:
这就说明,如果容许有一定误差,则可以用样本的分布去估计总体的分布.而且,在总体的分布不可能获得时,只能用样本的分布去估计总体的分布.
探索新知
用样本的分布来估计总体的分布
如果总体在每一个分组的频率记为 π1 , π2 ,…, πn,样本在每一组对应的频率记为p1 , p2 , …, pn,一般来说,
不等于零. 同样,大数定律可以保证,当样本的容量越来越大时,该式很小的可能性将越来越大.
典型例题
例 1 为了快速了解某学校学生体重(单位:kg)的大致情况,随机抽取了 10 名学生称重,得到的数据整理成茎叶图如图所示,估计这个学校学生体重的平均数和方差.
探索新知
(1) 在频率分布直方图中,众数是最高的小长方形的中点.
(2) 在样本中,有 50% 的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应相等.
(3) 平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形的底边中点的横坐标之和.
思考:怎样由频率分布直方图估计样本的众数、中位数、平均数?
典型例题
例 2 我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年 100 个家庭的月均用水量(单位:t),将数据按照 [0 , 1),[1 , 2),[2 , 3),[3 , 4),[4 , 5] 分成了 5 组,制成了如图所示频率分布直方图.
(1) 求图中 a 的值;
解:(1) 因为频率分布直方图所有矩形的面积之和为 1,所以
(0.12+0.22+0.36+a+0.12)×1=1,
解得 a=0.18.
典型例题
例 2 我国是世界上严重缺水的国家之一,某市为了制
定合理的节水方案,对家庭用水情况进行了调查,通
过抽样,获得了某年 100 个家庭的月均用水量(单位:
t),将数据按照 [0 , 1),[1 , 2),[2 , 3),[3 , 4),[4 , 5]
分成了 5 组,制成了如图所示频率分布直方图.
(2) 设该市有 10 万个家庭,估计全市月均用水量不低于 3t 的家庭数;
解:(2) 抽取的样本中,月均用水量不低于 3t 的家庭所占比例为
(a+0.12)×1=0.3=30%,
因此估计全市月均用水量不低于 3t 的家庭所占比例也为 30%,所求家庭数为 100 000×30%=30 000.
典型例题
例 2 我国是世界上严重缺水的国家之一,某市为了制
定合理的节水方案,对家庭用水情况进行了调查,通
过抽样,获得了某年 100 个家庭的月均用水量(单位:
t),将数据按照 [0 , 1),[1 , 2),[2 , 3),[3 , 4),[4 , 5]
分成了 5 组,制成了如图所示频率分布直方图.
(3) 假设同组中的每个数据都用该组区间的中间值代替,估计全市家庭月均用水量的平均数 .
解:(3) 因为
0.12×0.5+0.22×1.5+0.36×2.5+0.18×3.5+0.12×4.5=2.46,
所以估计全市家庭月均用水量的平均数为 2.46.
当堂检测
01
当堂检测
A
当堂检测
当堂检测
当堂检测
当堂检测
当堂检测
当堂检测
当堂检测
祝同学新学期新气象
感谢观看
人教B版(2019)必修第二册
第五章 统计与概率
5.1.4 用样本估计总体
学习目标
会用样本的数字特征估计总体的数字特征
01
能用样本的分布来估计总体的分布
02
探索新知
以下是某高校高一年级 98 位学生的身高(单位:cm):
已知这组数的总体平均数为 163.5,总体方差为 56.3.
161 168 166 168 152 152 163 164 170 167 143 166 153 165
168 167 163 157 160 159 153 169 172 175 165 161 158 172
147 164 171 149 158 155 169 150 173 170 162 157 152 180
178 158 162 164 172 165 165 155 163 178 159 168 161 151
168 168 165 158 162 165 163 166 174 163 163 175 165 160
161 177 163 170 155 156 161 169 167 151 156 158 165 179
161 176 162 168 153 169 155 165 163 166 172 160 173 164
用简单随机抽样的方法从总体中抽取容量为 10 的样本 3 次,分别计算样本平均数与样本方差,并与总体对应的值进行比较.
情境与问题
探索新知
用简单随机抽样样本的数字特征估计总体的数字特征
一般情况下,如果样本的容量恰当,抽样方法又合理的话,样本的特征能够反映总体的特征.特别地,样本平均数(也称为样本均值)、方差(也称为样本方差)与总体对应的值相差不会太大.
例如,上述数据中,如果用简单随机抽样抽得的序号分别为 90,35,63,68,66,9,30,56,50,49,则对应的样本为:169,169,163,175,163,170,164,151,155,165,容易算出,样本均值为 164.4,样本方差为 45.84,它们与总体对应的值差别都不大.
这就说明 , 在容许一定误差存在的前提下 , 可以用样本的数字特征去估计总体的数字特征 , 这样就能节省人力和物力等.
探索新知
用简单随机抽样样本的数字特征估计总体的数字特征
另外,有时候总体的数字特征不可能获得,比如质监部门想知道市场上节能灯的平均使用寿命,不可能把所有节能灯都拿来检测,此时只能用样本的数字特征去估计总体的数字特征.
一般来说,在估计总体的数字特征时,只需直接算出样本对应的数字特征即可.
需要强调的是,估计一般是有误差的. 例如,如果总体平均数记为 ,样本均值记为 ,一般来说,,, 都有可能. 但是,大数定律可以保证,当样本的容量越来越大时,估计的误差很小的可能性将越来越大.
情境与问题
在考察某中学的学生的平均身高时,如果采用分层抽样的方法,得到了男生身高的平均数为 170,方差为 16;女生身高的平均数为 165,方差为 25.
(1)如果没有其它信息,怎样估计总体的平均数与方差?
(2)如果知道抽取的样本中,男生有 20 人,女生有 15 人,怎么估计总体的平均数与方差?
方法一:作为估计来说,我们可以选择男生(或女生)样本的平均数与方差作为总体对应值的估计,但这样的选择没有充分利用已知的数据,显然不够好.
探索新知
情境与问题
探索新知
在考察某中学的学生的平均身高时,如果采用分层抽样的方法,得到了男生身高的平均数为 170,方差为 16;女生身高的平均数为 165,方差为 25.
(1)如果没有其它信息,怎样估计总体的平均数与方差?
(2)如果知道抽取的样本中,男生有 20 人,女生有 15 人,怎么估计总体的平均数与方差?
方法二:取每一层样本数字特征的算术平均值作为总体的估计,即估
计总体平均数为 ,
类似地,总体方差可估计为 .
探索新知
但第二种估计方法也还不太理想,因为对于分层抽样来说,每一层所抽取的个体数目一般来说是不相等的,简单的求数字特征的算术平均值体现不出这一点.
怎样才能体现这一点呢?尤其是,当我们把各层中得到的个体放在一起作为一个样本时,样本均值与样本方差该如何计算呢?
此时,当然可以把各层数据集中在一起来重新计算,但也可以去考虑整个样本的数字特征与每一层的数字特征之间的关系来实现,后者在大数据时代的并行计算中经常使用.
探索新知
我们以分两层抽样的情况为例.
假设第一层抽取 m 个数,分别为 x1 , x2 ,…, xm,平均数为 ,方差为 s2;第二层抽取 n 个数,分别为 y1 , y2 ,…, yn,平均数为 ,方差为 t2. 则
依照上述公式可以算出,前述尝试与发现(2)中总体的平均数可以估计为 167.86,总体的方差可以估计为 25.98.
探索新知
分层抽样的均值与方差
一般地,设样本中不同层的平均数分别为 ,…,,方差分别为 ,…,,,相应的权重分别为 ,则
平均数:
方差:
情境与问题
探索新知
通过对某中学 1 257 名高一学生期中考试的数学成绩(具体数据参见这一小节的附录)进行整理,可以得到如下数据,并由此可作出频率分布直方图和折线图,如图所示.
从附录的数据中抽取容量为 100 的样本,整理类似的表格,并制作频率分布直方图.
探索新知
同前面一样,如果样本的容量恰当,抽样方法又合理的话,样本的分布与总体分布会差不多.特别地,每一组的频率与总体对应的频率相差不会太大.
如果从上述尝试与发现中提到的数据中,抽取两个容量为 100 的样本(分别记为样本 A,样本 B,具体数据参见这一小节的附录),则可以得到如下频数、频率对应表:
探索新知
它们的频率分布直方图分别如图 (1) (2) 所示:
这就说明,如果容许有一定误差,则可以用样本的分布去估计总体的分布.而且,在总体的分布不可能获得时,只能用样本的分布去估计总体的分布.
探索新知
用样本的分布来估计总体的分布
如果总体在每一个分组的频率记为 π1 , π2 ,…, πn,样本在每一组对应的频率记为p1 , p2 , …, pn,一般来说,
不等于零. 同样,大数定律可以保证,当样本的容量越来越大时,该式很小的可能性将越来越大.
典型例题
例 1 为了快速了解某学校学生体重(单位:kg)的大致情况,随机抽取了 10 名学生称重,得到的数据整理成茎叶图如图所示,估计这个学校学生体重的平均数和方差.
探索新知
(1) 在频率分布直方图中,众数是最高的小长方形的中点.
(2) 在样本中,有 50% 的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应相等.
(3) 平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形的底边中点的横坐标之和.
思考:怎样由频率分布直方图估计样本的众数、中位数、平均数?
典型例题
例 2 我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年 100 个家庭的月均用水量(单位:t),将数据按照 [0 , 1),[1 , 2),[2 , 3),[3 , 4),[4 , 5] 分成了 5 组,制成了如图所示频率分布直方图.
(1) 求图中 a 的值;
解:(1) 因为频率分布直方图所有矩形的面积之和为 1,所以
(0.12+0.22+0.36+a+0.12)×1=1,
解得 a=0.18.
典型例题
例 2 我国是世界上严重缺水的国家之一,某市为了制
定合理的节水方案,对家庭用水情况进行了调查,通
过抽样,获得了某年 100 个家庭的月均用水量(单位:
t),将数据按照 [0 , 1),[1 , 2),[2 , 3),[3 , 4),[4 , 5]
分成了 5 组,制成了如图所示频率分布直方图.
(2) 设该市有 10 万个家庭,估计全市月均用水量不低于 3t 的家庭数;
解:(2) 抽取的样本中,月均用水量不低于 3t 的家庭所占比例为
(a+0.12)×1=0.3=30%,
因此估计全市月均用水量不低于 3t 的家庭所占比例也为 30%,所求家庭数为 100 000×30%=30 000.
典型例题
例 2 我国是世界上严重缺水的国家之一,某市为了制
定合理的节水方案,对家庭用水情况进行了调查,通
过抽样,获得了某年 100 个家庭的月均用水量(单位:
t),将数据按照 [0 , 1),[1 , 2),[2 , 3),[3 , 4),[4 , 5]
分成了 5 组,制成了如图所示频率分布直方图.
(3) 假设同组中的每个数据都用该组区间的中间值代替,估计全市家庭月均用水量的平均数 .
解:(3) 因为
0.12×0.5+0.22×1.5+0.36×2.5+0.18×3.5+0.12×4.5=2.46,
所以估计全市家庭月均用水量的平均数为 2.46.
当堂检测
01
当堂检测
A
当堂检测
当堂检测
当堂检测
当堂检测
当堂检测
当堂检测
当堂检测
祝同学新学期新气象
感谢观看
