5.1.3 数据的直观表示(教学课件)__高中数学人教B版(2019)必修第二册(共38张PPT)
文档属性
| 名称 | 5.1.3 数据的直观表示(教学课件)__高中数学人教B版(2019)必修第二册(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 07:17:39 | ||
图片预览







文档简介
(共36张PPT)
人教B版(2019)必修第二册
第五章 统计与概率
5.1.3 数据的直观表示
学习目标
了解柱形图、折线图的意义
01
了解扇形图的意义
02
理解茎叶图及其含义
03
理解频数分布直方图和频率分布直方图的重要性
04
情境与问题
探索新知
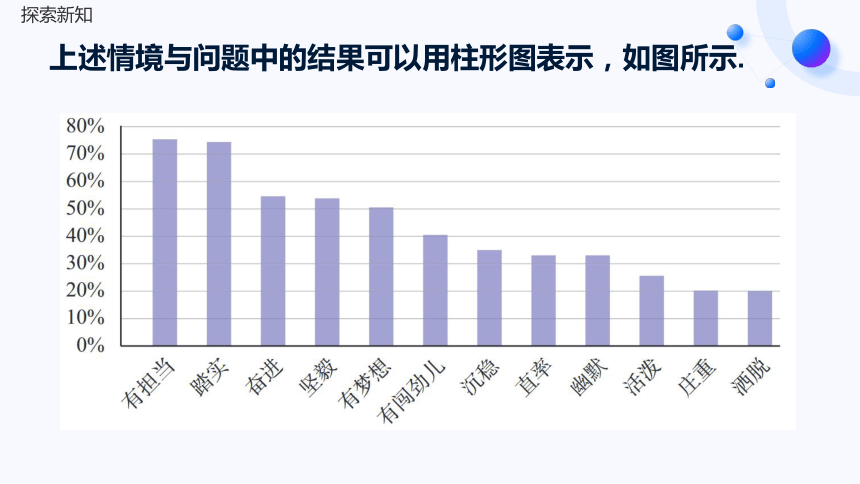
2015 年 7 月 6 日的《中国青年报》报道:“根据调查,有担当(76.3%)和踏实(74.5%)的年轻人最受访者欣赏.奋进(54.7%)、坚毅(54.1%)、有梦想(50.2%)、有闯劲儿(40.1%)、沉稳(36.7%)、直率(34.6%)、幽默(33.4%)、活泼(27.2%)、庄重(20.3%)、洒脱(20.0%)也是受访者欣赏的品质.
你能将这一调查结果用图表进行形象化表示吗?
探索新知
上述情境与问题中的结果可以用柱形图表示,如图所示.
探索新知
柱形图:柱形图(也叫条形图)可以形象地比较各个数据之间的数量关系.
柱形图的特点:
(1) 横轴代表所关注的数据类型;
(2) 纵轴是对应的数量、个数或比例;
(3) 每一个矩形都是等宽的,矩形的高表示相应的数量.
柱形图
情境与问题
探索新知
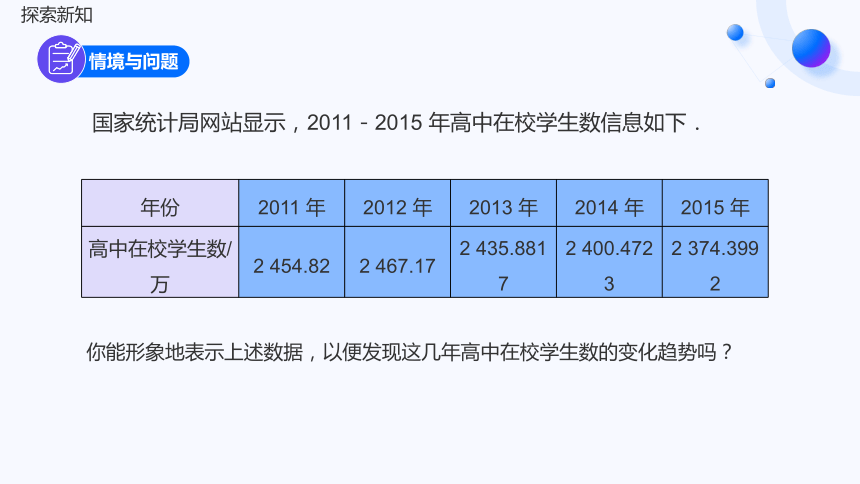
国家统计局网站显示,2011-2015 年高中在校学生数信息如下.
你能形象地表示上述数据,以便发现这几年高中在校学生数的变化趋势吗?
年份 2011 年 2012 年 2013 年 2014 年 2015 年
高中在校学生数/万 2 454.82 2 467.17 2 435.881 7 2 400.472 3 2 374.399 2
探索新知
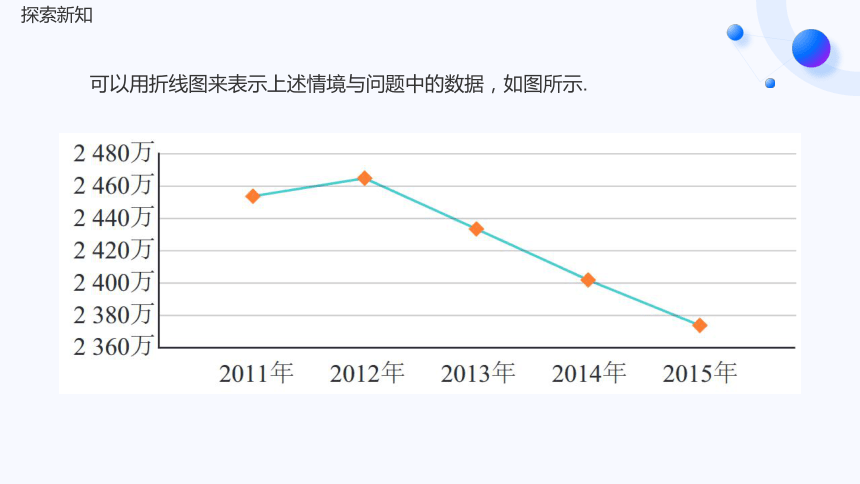
可以用折线图来表示上述情境与问题中的数据,如图所示.
探索新知
折线图:用折线的升降来表示统计数据的变化趋势.
折线图的特点:
(1) 折线图横轴可以是时间等变量;
(2) 纵轴是统计量的数量;
(3) 折线图表示数据随时间变化的趋势更有优势.
折线图
情境与问题
探索新知
2016 年 12 月 17 日至 21 日期间,北京市空气质量呈现重度及以上污染水平,经北京市政府批准,12 月 16 日 20 时至 21 日 24 时,北京市启动了空气重污染红色预警,期间实行了机动车“单双号”现行等措施.《中国青年报》社会调查中心联合问卷网,对 2 002 人进行了调查,得到了以下数据:647 人非常支持,891 人支持,348 人态度一般,116人不支持.
如果你是《中国青年报》的记者,你会怎样整理和报道这些数据?
探索新知
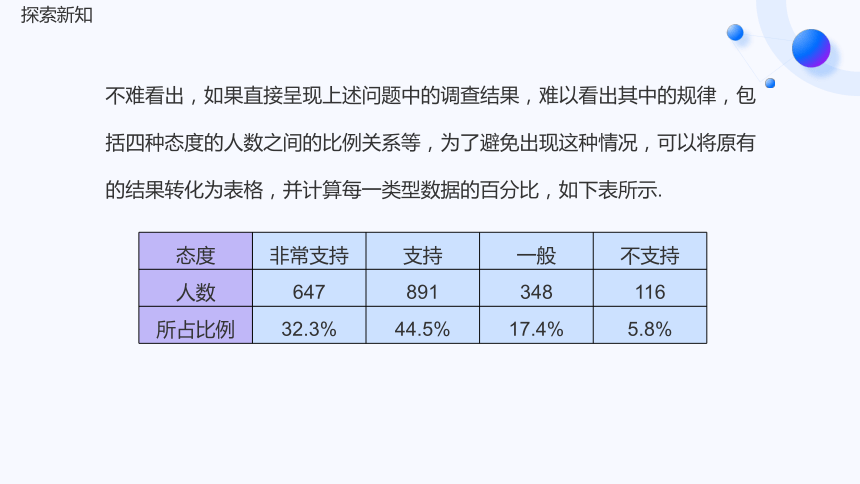
不难看出,如果直接呈现上述问题中的调查结果,难以看出其中的规律,包括四种态度的人数之间的比例关系等,为了避免出现这种情况,可以将原有的结果转化为表格,并计算每一类型数据的百分比,如下表所示.
态度 非常支持 支持 一般 不支持
人数 647 891 348 116
所占比例 32.3% 44.5% 17.4% 5.8%
探索新知
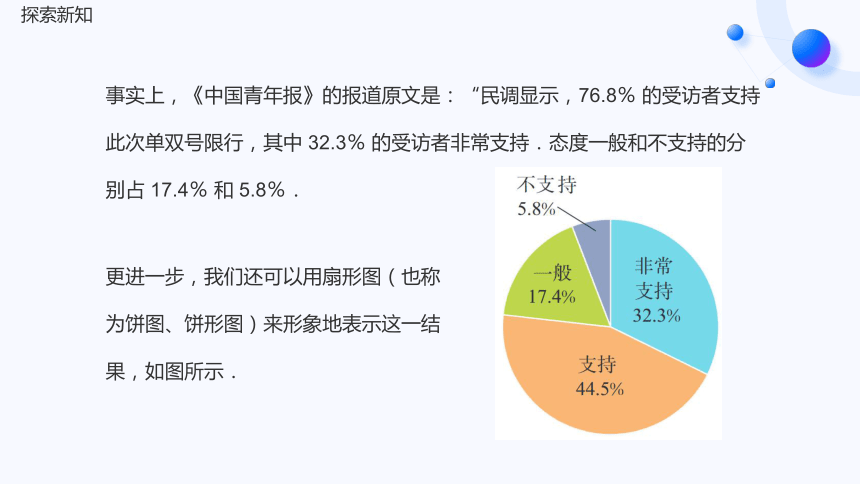
事实上,《中国青年报》的报道原文是:“民调显示,76.8% 的受访者支持此次单双号限行,其中 32.3% 的受访者非常支持.态度一般和不支持的分别占 17.4% 和 5.8%.
更进一步,我们还可以用扇形图(也称为饼图、饼形图)来形象地表示这一结果,如图所示.
探索新知
扇形图也称为饼图、饼形图
扇形图的特点:
(1) 用圆代表整体,用扇形代表各部分,图中每一个扇形的圆心角以及弧长都与这一部分表示的数据大小成正比;
(2) 能直观形象地表达整体与部分的关系.
扇形图
探索新知
柱形图(条形图) 折线图 扇形图
优点 ①可以直观地反映数据分布的大致情况; ②可以清楚地表示出每个项目中具体数目,易于比较数据之间的差别 折线图不但可以表示数量的多少,而且能够用折线的起伏清楚直观地表示数量的增减变化的情况 可以形象地表示出各部分数据在全部数据中所占的比例情况
缺点 会损失数据的部分信息且不能明显显示部分与整体的关系 不能直观反映数据的分布情况且不适合总体分布较多的情况 扇形图中没有具体的数据,不能够看出各部分具体的数量和差距
情境与问题
探索新知
某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲:12,12,24,24,31,31,36,36,37,39,44,49,50;
乙:8,13,13,14,16,23,26,29,33,35,38,39,51.
这两组数据可以用下图来表示.
你能说出上述图是怎样构造出来的吗?由图中可以得出甲、乙两名运动员得分的哪些信息?
探索新知
一般来说,茎叶图中,所有的茎都竖直排列,而叶沿水平方向排列.茎叶图也可以只表示一组数.
类似右图的图称为茎叶图,其名称的由来是因为它的中间像植物的茎,两边像植物茎上生长的叶子.图中,中间的数字表示两位运动员得分的十位数,两边的数字表示得分的个位数.
茎叶图
探索新知
将一组数整理成茎叶图后,如果每一行的数都是按从大到小(或从小到大)顺序排列,则从中可以方便地看出这组数的最值、中位数等数字特征.例如,从图中可以看出:甲得分的最大值是 50,最小值是 12,中位数为 36;乙得分的最大值是 ,最小值是 ,中位数为 .
51
8
26
茎叶图
探索新知
另外,从茎叶图中还可以看出一组数的分布情况,从而可能可以得到一些额外的信息.例如,从图中可以看出:甲的得分大多数集中在 [30 , 40),而且小于 31 分和大于 39 分的次数相差不多,因此可以估计出甲的平均数应该在区间 [30 , 40) 内;类似地,可以估计出乙得分的平均数应该在区间 内.
[20 , 30)
茎叶图
探索新知
从图中我们还可以估计出甲得分和乙得分的方差的相对大小,因为甲得分的数据比较集中,乙得分的数据比较分散,两者的数据个数相等,所以可以得出:甲得分的方差小于乙得分的方差.
茎叶图
情境与问题
探索新知
以下是某学校全体学生一次政治考试的成绩.
(1)能否直接用前面提到过的图来表示上面的数据?为什么?
76 83 88 89 72 67 88 85 90 87 74 65 86 71 88
90 82 90 81 78 76 75 78 86 79 71 73 82 76 90
······
90 76 86 88 86
前边的直观表示方法都是直接引用数据,这里数据众多,直接引用不方便,价值也不大,所以不能用前边的几种直观表示方法表示.
情境与问题
探索新知
以下是某学校全体学生一次政治考试的成绩.
(2)怎样才能直观地表示出上述数据的大致分布情况?
一个自然的想法是,将数据按照一定的方式进行“压缩”,然后再用图来直观地表示压缩后的数据.
76 83 88 89 72 67 88 85 90 87 74 65 86 71 88
90 82 90 81 78 76 75 78 86 79 71 73 82 76 90
······
90 76 86 88 86
探索新知
(1)找出最值,计算极差
上述成绩的最小值是 59,最大值是 94,因此极差为 35.
(2)合理分组,确定区间
数据共有 245 个 , 可以分为 8~12 组 , 这里取 8 组 , 并且按照从 55 分开始 , 组距为 5 确定计数区间 ,即区间为 [55,60),[60,65),…,[85,90),[90,95].
画频率分布直方图的方法步骤:
频数分布直方图与频率分布直方图
探索新知
(3)整理数据
逐个检查原始数据,统计每个区间内数的个数(称为区间对应的频数),并求出频数与数据个数的比值(称为区间对应的频率),如下表所示(频率精确到 0.01).
探索新知
(4)作出有关图示
根据上述整理后的数据,可以作出频数分布直方图与频率分布直方图,分别如图(1)(2)所示.值得注意的是,频数分布直方图的纵坐标是频数,每一组数对应的矩形高度与频数成正比;频率分布直方图的纵坐标是频率/组距,每一组数对应的矩形高度与频率成正比,而且每个矩形的面积等于这一组数对应的频率,从而可知频率分布直方图中,所有矩形的面积之和为 1.
探索新知
频率(数)分布直方图的特点与优势:
(1) 原有数据被“压缩”了,从这两种图中也得不到所有原始数据,也无法恢复成原始数据.
(2) 可以清楚的看出数据的分布趋势,也可以得出有关数字特征的大致情况. 比如,估计出平均数、中位数、百分位数、方差. 当然,利用直方图估计出的这些数字特征与利用原始数据求出的数字特征一般会有差异.
典型例题
例 1 为了了解学生的课业负担,甲、乙两所学校分别抽取了 200 名在校生,了解他们完成作业所需时间,并分别作出了频数分布直方图如图(1)(2)所示,其中分组的区间都为 [0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3].记甲学校所得数据的中位数为 x,乙学校所得数据的中位数为 y,判断 x 和 y 的相对大小.
解:由图(1)可以看出,x ∈ [2,2.5);由图(2)可以看出,y ∈ [1.5,2).因此 x>y.
典型例题
例 2 某射击运动员一次射击训练的成绩可以整理成图所示的统计图表,试计算这次成绩的平均数与方差.
探索新知
借助计算机软件,可以快捷地作出有关统计图表.例如,本小节一开始的柱形图,在 Excel 中输入有关数据后,就可以用有关作图命令画出来,而且可以方便地改变呈现形式.
在 GeoGebra 软件中,利用表格区输入数据,然后利用“单变量分析”,可以得到数据的直方图等信息,而且各种参数都可以自行设定.例如,前面提到的频数分布直方图与折线图可用 GeoGebra 作出,如图所示.
用信息技术对数据进行整理和作统计图表
当堂检测
当堂检测
C
当堂检测
D
当堂检测
D
当堂检测
A
当堂检测
A
当堂检测
当堂检测
祝同学新学期新气象
感谢观看
人教B版(2019)必修第二册
第五章 统计与概率
5.1.3 数据的直观表示
学习目标
了解柱形图、折线图的意义
01
了解扇形图的意义
02
理解茎叶图及其含义
03
理解频数分布直方图和频率分布直方图的重要性
04
情境与问题
探索新知
2015 年 7 月 6 日的《中国青年报》报道:“根据调查,有担当(76.3%)和踏实(74.5%)的年轻人最受访者欣赏.奋进(54.7%)、坚毅(54.1%)、有梦想(50.2%)、有闯劲儿(40.1%)、沉稳(36.7%)、直率(34.6%)、幽默(33.4%)、活泼(27.2%)、庄重(20.3%)、洒脱(20.0%)也是受访者欣赏的品质.
你能将这一调查结果用图表进行形象化表示吗?
探索新知
上述情境与问题中的结果可以用柱形图表示,如图所示.
探索新知
柱形图:柱形图(也叫条形图)可以形象地比较各个数据之间的数量关系.
柱形图的特点:
(1) 横轴代表所关注的数据类型;
(2) 纵轴是对应的数量、个数或比例;
(3) 每一个矩形都是等宽的,矩形的高表示相应的数量.
柱形图
情境与问题
探索新知
国家统计局网站显示,2011-2015 年高中在校学生数信息如下.
你能形象地表示上述数据,以便发现这几年高中在校学生数的变化趋势吗?
年份 2011 年 2012 年 2013 年 2014 年 2015 年
高中在校学生数/万 2 454.82 2 467.17 2 435.881 7 2 400.472 3 2 374.399 2
探索新知
可以用折线图来表示上述情境与问题中的数据,如图所示.
探索新知
折线图:用折线的升降来表示统计数据的变化趋势.
折线图的特点:
(1) 折线图横轴可以是时间等变量;
(2) 纵轴是统计量的数量;
(3) 折线图表示数据随时间变化的趋势更有优势.
折线图
情境与问题
探索新知
2016 年 12 月 17 日至 21 日期间,北京市空气质量呈现重度及以上污染水平,经北京市政府批准,12 月 16 日 20 时至 21 日 24 时,北京市启动了空气重污染红色预警,期间实行了机动车“单双号”现行等措施.《中国青年报》社会调查中心联合问卷网,对 2 002 人进行了调查,得到了以下数据:647 人非常支持,891 人支持,348 人态度一般,116人不支持.
如果你是《中国青年报》的记者,你会怎样整理和报道这些数据?
探索新知
不难看出,如果直接呈现上述问题中的调查结果,难以看出其中的规律,包括四种态度的人数之间的比例关系等,为了避免出现这种情况,可以将原有的结果转化为表格,并计算每一类型数据的百分比,如下表所示.
态度 非常支持 支持 一般 不支持
人数 647 891 348 116
所占比例 32.3% 44.5% 17.4% 5.8%
探索新知
事实上,《中国青年报》的报道原文是:“民调显示,76.8% 的受访者支持此次单双号限行,其中 32.3% 的受访者非常支持.态度一般和不支持的分别占 17.4% 和 5.8%.
更进一步,我们还可以用扇形图(也称为饼图、饼形图)来形象地表示这一结果,如图所示.
探索新知
扇形图也称为饼图、饼形图
扇形图的特点:
(1) 用圆代表整体,用扇形代表各部分,图中每一个扇形的圆心角以及弧长都与这一部分表示的数据大小成正比;
(2) 能直观形象地表达整体与部分的关系.
扇形图
探索新知
柱形图(条形图) 折线图 扇形图
优点 ①可以直观地反映数据分布的大致情况; ②可以清楚地表示出每个项目中具体数目,易于比较数据之间的差别 折线图不但可以表示数量的多少,而且能够用折线的起伏清楚直观地表示数量的增减变化的情况 可以形象地表示出各部分数据在全部数据中所占的比例情况
缺点 会损失数据的部分信息且不能明显显示部分与整体的关系 不能直观反映数据的分布情况且不适合总体分布较多的情况 扇形图中没有具体的数据,不能够看出各部分具体的数量和差距
情境与问题
探索新知
某赛季甲、乙两名篮球运动员每场比赛的得分情况如下:
甲:12,12,24,24,31,31,36,36,37,39,44,49,50;
乙:8,13,13,14,16,23,26,29,33,35,38,39,51.
这两组数据可以用下图来表示.
你能说出上述图是怎样构造出来的吗?由图中可以得出甲、乙两名运动员得分的哪些信息?
探索新知
一般来说,茎叶图中,所有的茎都竖直排列,而叶沿水平方向排列.茎叶图也可以只表示一组数.
类似右图的图称为茎叶图,其名称的由来是因为它的中间像植物的茎,两边像植物茎上生长的叶子.图中,中间的数字表示两位运动员得分的十位数,两边的数字表示得分的个位数.
茎叶图
探索新知
将一组数整理成茎叶图后,如果每一行的数都是按从大到小(或从小到大)顺序排列,则从中可以方便地看出这组数的最值、中位数等数字特征.例如,从图中可以看出:甲得分的最大值是 50,最小值是 12,中位数为 36;乙得分的最大值是 ,最小值是 ,中位数为 .
51
8
26
茎叶图
探索新知
另外,从茎叶图中还可以看出一组数的分布情况,从而可能可以得到一些额外的信息.例如,从图中可以看出:甲的得分大多数集中在 [30 , 40),而且小于 31 分和大于 39 分的次数相差不多,因此可以估计出甲的平均数应该在区间 [30 , 40) 内;类似地,可以估计出乙得分的平均数应该在区间 内.
[20 , 30)
茎叶图
探索新知
从图中我们还可以估计出甲得分和乙得分的方差的相对大小,因为甲得分的数据比较集中,乙得分的数据比较分散,两者的数据个数相等,所以可以得出:甲得分的方差小于乙得分的方差.
茎叶图
情境与问题
探索新知
以下是某学校全体学生一次政治考试的成绩.
(1)能否直接用前面提到过的图来表示上面的数据?为什么?
76 83 88 89 72 67 88 85 90 87 74 65 86 71 88
90 82 90 81 78 76 75 78 86 79 71 73 82 76 90
······
90 76 86 88 86
前边的直观表示方法都是直接引用数据,这里数据众多,直接引用不方便,价值也不大,所以不能用前边的几种直观表示方法表示.
情境与问题
探索新知
以下是某学校全体学生一次政治考试的成绩.
(2)怎样才能直观地表示出上述数据的大致分布情况?
一个自然的想法是,将数据按照一定的方式进行“压缩”,然后再用图来直观地表示压缩后的数据.
76 83 88 89 72 67 88 85 90 87 74 65 86 71 88
90 82 90 81 78 76 75 78 86 79 71 73 82 76 90
······
90 76 86 88 86
探索新知
(1)找出最值,计算极差
上述成绩的最小值是 59,最大值是 94,因此极差为 35.
(2)合理分组,确定区间
数据共有 245 个 , 可以分为 8~12 组 , 这里取 8 组 , 并且按照从 55 分开始 , 组距为 5 确定计数区间 ,即区间为 [55,60),[60,65),…,[85,90),[90,95].
画频率分布直方图的方法步骤:
频数分布直方图与频率分布直方图
探索新知
(3)整理数据
逐个检查原始数据,统计每个区间内数的个数(称为区间对应的频数),并求出频数与数据个数的比值(称为区间对应的频率),如下表所示(频率精确到 0.01).
探索新知
(4)作出有关图示
根据上述整理后的数据,可以作出频数分布直方图与频率分布直方图,分别如图(1)(2)所示.值得注意的是,频数分布直方图的纵坐标是频数,每一组数对应的矩形高度与频数成正比;频率分布直方图的纵坐标是频率/组距,每一组数对应的矩形高度与频率成正比,而且每个矩形的面积等于这一组数对应的频率,从而可知频率分布直方图中,所有矩形的面积之和为 1.
探索新知
频率(数)分布直方图的特点与优势:
(1) 原有数据被“压缩”了,从这两种图中也得不到所有原始数据,也无法恢复成原始数据.
(2) 可以清楚的看出数据的分布趋势,也可以得出有关数字特征的大致情况. 比如,估计出平均数、中位数、百分位数、方差. 当然,利用直方图估计出的这些数字特征与利用原始数据求出的数字特征一般会有差异.
典型例题
例 1 为了了解学生的课业负担,甲、乙两所学校分别抽取了 200 名在校生,了解他们完成作业所需时间,并分别作出了频数分布直方图如图(1)(2)所示,其中分组的区间都为 [0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3].记甲学校所得数据的中位数为 x,乙学校所得数据的中位数为 y,判断 x 和 y 的相对大小.
解:由图(1)可以看出,x ∈ [2,2.5);由图(2)可以看出,y ∈ [1.5,2).因此 x>y.
典型例题
例 2 某射击运动员一次射击训练的成绩可以整理成图所示的统计图表,试计算这次成绩的平均数与方差.
探索新知
借助计算机软件,可以快捷地作出有关统计图表.例如,本小节一开始的柱形图,在 Excel 中输入有关数据后,就可以用有关作图命令画出来,而且可以方便地改变呈现形式.
在 GeoGebra 软件中,利用表格区输入数据,然后利用“单变量分析”,可以得到数据的直方图等信息,而且各种参数都可以自行设定.例如,前面提到的频数分布直方图与折线图可用 GeoGebra 作出,如图所示.
用信息技术对数据进行整理和作统计图表
当堂检测
当堂检测
C
当堂检测
D
当堂检测
D
当堂检测
A
当堂检测
A
当堂检测
当堂检测
祝同学新学期新气象
感谢观看
