4.5.1 机械能守恒定律(共18张ppt)
文档属性
| 名称 | 4.5.1 机械能守恒定律(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 23:27:52 | ||
图片预览



文档简介
(共18张PPT)
粤教版 必修二 第四章
第四章 机械能及守恒定律
第五节 机械能守恒定律
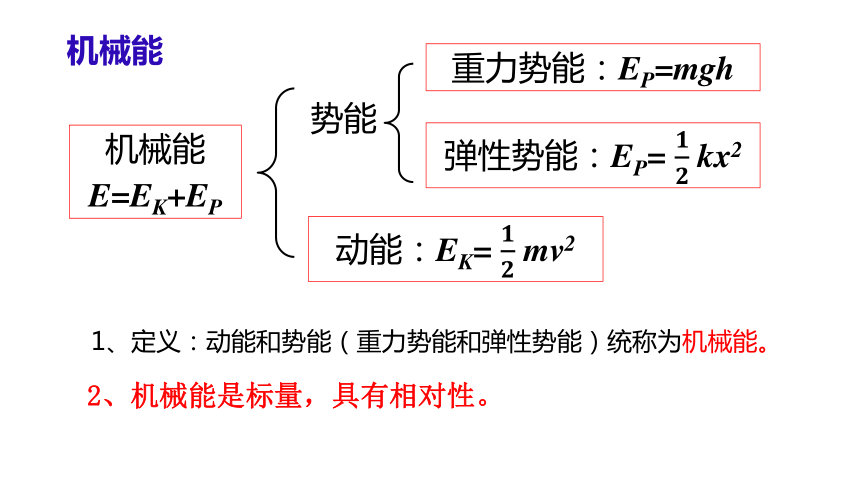
动能:EK= mv2
势能
重力势能:EP=mgh
弹性势能:EP= kx2
机械能
E=EK+EP
机械能
1、定义:动能和势能(重力势能和弹性势能)统称为机械能。
2、机械能是标量,具有相对性。
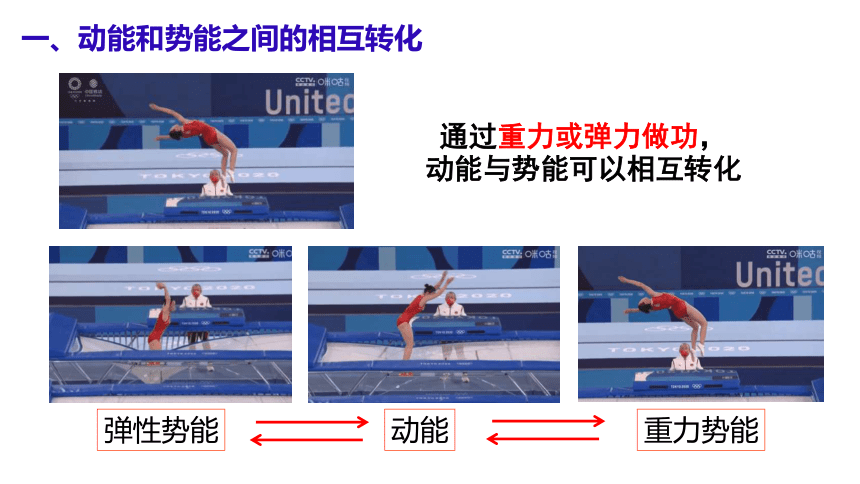
一、动能和势能之间的相互转化
弹性势能
动能
重力势能
通过重力或弹力做功,
动能与势能可以相互转化
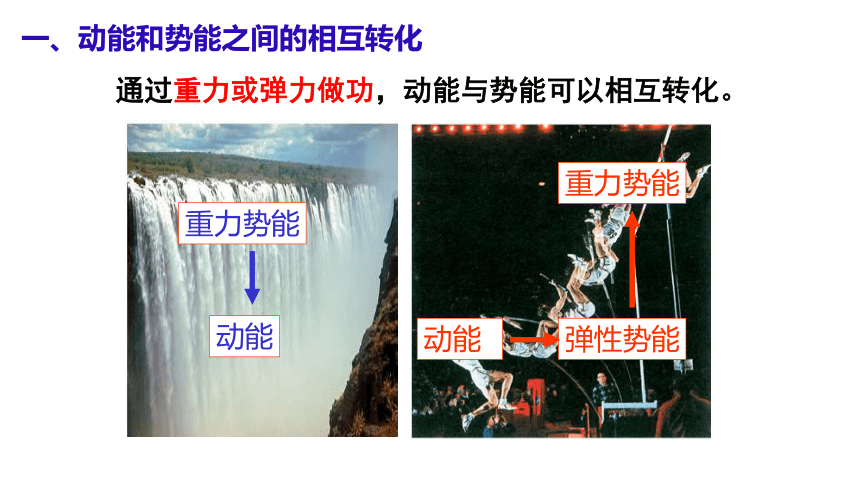
一、动能和势能之间的相互转化
重力势能
动能
动能
弹性势能
重力势能
通过重力或弹力做功,动能与势能可以相互转化。
生活中的现象
某些汽车或列车站的站台都设计有一个小的坡度。这是为什么?
进站前关闭发动机,机车凭惯性上坡,动能变成势能储存起来,出站时下坡,势能变成动能,节省了能源。
动能与势能的相互转化是否存在某种定量关系
情境1:质量为m的小球从点A开始自由下落
机械能守恒:EP1 + Ek1 = EP2 + Ek2
机械能守恒条件:只有重力做功(单个物体)
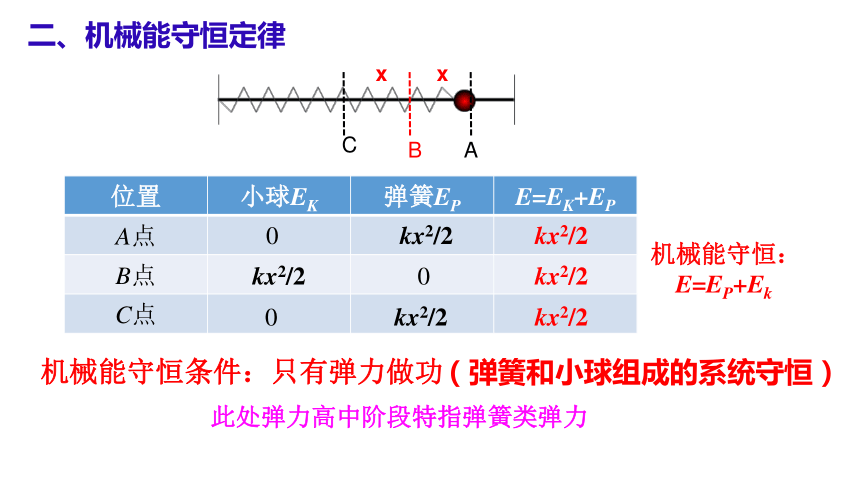
二、机械能守恒定律
A
B
C
x
x
位置 小球EK 弹簧EP E=EK+EP
A点
B点
C点
0
0
0
kx2/2
kx2/2
kx2/2
kx2/2
kx2/2
kx2/2
机械能守恒:
E=EP+Ek
(弹簧和小球组成的系统守恒)
机械能守恒条件:只有弹力做功
此处弹力高中阶段特指弹簧类弹力
二、机械能守恒定律
1. 内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
2. 表达式:
守恒观点
(1)EK2+EP2=EK1+EP1 即 E2=E1
转化观点
转移观点
或 ΔEk减=ΔEp增
或 ΔEA减=ΔEB增
(3)ΔEA=-ΔEB
(2)ΔEk= -ΔEp
注意零势面选取
关注初、末状态动能和势能的变化量
二、机械能守恒定律
关注系统不同物体机械能的变化量
3. 机械能守恒的条件:
(1)系统内只有重力和弹簧弹力做功.
(理解:并非不受其它力,指的是除重力和弹簧弹力以外的力不做功或做功的代数和为零)
(2)系统内只有动能和势能的相互转化,而没有其它形式能量参与转化。
二、机械能守恒定律
在拉力作用下沿斜面向上运动的物体。F=f
自由落体运动的小球
从A向O摆动的摆球
只受重力作用只有重力做功
受重力和其他力只有重力做功
受重力和其他作用力,重力做功外,其他作用力做功的代数和为零
举例:
物体系统只受重力和弹簧弹力,不受其他力。
小球和弹簧组成的系统。
例1 (多选)如图所示,下列关于机械能是否守恒的判断正确的是( )
甲图中,物体将弹簧压缩的过程中,物体和弹簧组成的系统机械能守恒(不计空气阻力)
乙图中,物体在大小等于摩擦力的沿斜面向下的拉力F作用下沿斜面下滑时,物体机械能守恒
丙图中,物体沿斜面匀速下滑的过程中,物体机械能守恒
丁图中,固定的斜面光滑,物体沿斜面下滑的过程中,物体机械能守恒
ABD
情境:各接触面光滑,A自B上端自由下滑的过程中,
A、B及两者组成的系统机械能如何变化?
只有重力和A、B间的弹力做功
——系统机械能守恒
A、B组成的系统:
A物体:
B对A的弹力做负功,这个力对A来说是外力
——机械能不守恒(减少)
B物体:
A对B的弹力做正功,这个力对B来说是外力
——机械能不守恒(增加)
例2 (多选) 如图,一根轻弹簧下端固定,竖立在水平地面上.其上方A位置有一小球,小球从静止开始下落,在B位置时刚接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.不计空气阻力,则小球( )
A. 下落至C位置时速度最大
B. 由A至D下落过程中机械能守恒
C. 由B至D的过程中,动能先增大后减小
D. 由A至D的过程中重力势能的减少量等于弹簧弹性势能的增加量
ACD
例3 如图所示,从某高度处,将质量为m的小球斜向上方抛出,初速度为v0,小球到达最高点时的速度为v1,最大高度为h,重力加速度为g。以地面为参考平面,不计空气阻力。下列正确的是( )
A.落地时,小球的动能为
B.抛出时,小球的机械能为 mgh
C.抛出时,小球的重力势能为 mgh
D.抛出时,人对小球做功为
A
1. 选取研究对象(物体或系统)和研究过程;
应用机械能守恒定律解题的一般步骤:
2. 判断机械能是否守恒(是否只有重力或弹簧弹力做功);
3. 确定研究对象初、末状态的机械能(恰当选取参考平面);
4. 根据机械能守恒定律列方程求解。
应用机械能守恒定律解题,只需考虑过程的初、末状态,不必考虑两个状态间过程的细节,这是它的优点。
例4 如图所示,一端与墙相连的水平轻弹簧处于自由伸长状态,质量为4 kg的木块沿光滑的水平面以5 m/s的速度开始运动并挤压弹簧,不计空气阻力,求:
(1)弹簧的最大弹性势能;
(2)木块被弹回速度增大到3 m/s时弹簧的弹性势能。
机械能守恒定律和动能定理的比较:
在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
1、内容:
2、表达式:
3、守恒条件:
只有重力做功或弹力做功,其他力做功为0.
小结
ΔEk=ΔEp
EK2+EP2=EK1+EP1
ΔEA=-ΔEB
此处弹力高中阶段特指弹簧类弹力
粤教版 必修二 第四章
第四章 机械能及守恒定律
第五节 机械能守恒定律
动能:EK= mv2
势能
重力势能:EP=mgh
弹性势能:EP= kx2
机械能
E=EK+EP
机械能
1、定义:动能和势能(重力势能和弹性势能)统称为机械能。
2、机械能是标量,具有相对性。
一、动能和势能之间的相互转化
弹性势能
动能
重力势能
通过重力或弹力做功,
动能与势能可以相互转化
一、动能和势能之间的相互转化
重力势能
动能
动能
弹性势能
重力势能
通过重力或弹力做功,动能与势能可以相互转化。
生活中的现象
某些汽车或列车站的站台都设计有一个小的坡度。这是为什么?
进站前关闭发动机,机车凭惯性上坡,动能变成势能储存起来,出站时下坡,势能变成动能,节省了能源。
动能与势能的相互转化是否存在某种定量关系
情境1:质量为m的小球从点A开始自由下落
机械能守恒:EP1 + Ek1 = EP2 + Ek2
机械能守恒条件:只有重力做功(单个物体)
二、机械能守恒定律
A
B
C
x
x
位置 小球EK 弹簧EP E=EK+EP
A点
B点
C点
0
0
0
kx2/2
kx2/2
kx2/2
kx2/2
kx2/2
kx2/2
机械能守恒:
E=EP+Ek
(弹簧和小球组成的系统守恒)
机械能守恒条件:只有弹力做功
此处弹力高中阶段特指弹簧类弹力
二、机械能守恒定律
1. 内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
2. 表达式:
守恒观点
(1)EK2+EP2=EK1+EP1 即 E2=E1
转化观点
转移观点
或 ΔEk减=ΔEp增
或 ΔEA减=ΔEB增
(3)ΔEA=-ΔEB
(2)ΔEk= -ΔEp
注意零势面选取
关注初、末状态动能和势能的变化量
二、机械能守恒定律
关注系统不同物体机械能的变化量
3. 机械能守恒的条件:
(1)系统内只有重力和弹簧弹力做功.
(理解:并非不受其它力,指的是除重力和弹簧弹力以外的力不做功或做功的代数和为零)
(2)系统内只有动能和势能的相互转化,而没有其它形式能量参与转化。
二、机械能守恒定律
在拉力作用下沿斜面向上运动的物体。F=f
自由落体运动的小球
从A向O摆动的摆球
只受重力作用只有重力做功
受重力和其他力只有重力做功
受重力和其他作用力,重力做功外,其他作用力做功的代数和为零
举例:
物体系统只受重力和弹簧弹力,不受其他力。
小球和弹簧组成的系统。
例1 (多选)如图所示,下列关于机械能是否守恒的判断正确的是( )
甲图中,物体将弹簧压缩的过程中,物体和弹簧组成的系统机械能守恒(不计空气阻力)
乙图中,物体在大小等于摩擦力的沿斜面向下的拉力F作用下沿斜面下滑时,物体机械能守恒
丙图中,物体沿斜面匀速下滑的过程中,物体机械能守恒
丁图中,固定的斜面光滑,物体沿斜面下滑的过程中,物体机械能守恒
ABD
情境:各接触面光滑,A自B上端自由下滑的过程中,
A、B及两者组成的系统机械能如何变化?
只有重力和A、B间的弹力做功
——系统机械能守恒
A、B组成的系统:
A物体:
B对A的弹力做负功,这个力对A来说是外力
——机械能不守恒(减少)
B物体:
A对B的弹力做正功,这个力对B来说是外力
——机械能不守恒(增加)
例2 (多选) 如图,一根轻弹簧下端固定,竖立在水平地面上.其上方A位置有一小球,小球从静止开始下落,在B位置时刚接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.不计空气阻力,则小球( )
A. 下落至C位置时速度最大
B. 由A至D下落过程中机械能守恒
C. 由B至D的过程中,动能先增大后减小
D. 由A至D的过程中重力势能的减少量等于弹簧弹性势能的增加量
ACD
例3 如图所示,从某高度处,将质量为m的小球斜向上方抛出,初速度为v0,小球到达最高点时的速度为v1,最大高度为h,重力加速度为g。以地面为参考平面,不计空气阻力。下列正确的是( )
A.落地时,小球的动能为
B.抛出时,小球的机械能为 mgh
C.抛出时,小球的重力势能为 mgh
D.抛出时,人对小球做功为
A
1. 选取研究对象(物体或系统)和研究过程;
应用机械能守恒定律解题的一般步骤:
2. 判断机械能是否守恒(是否只有重力或弹簧弹力做功);
3. 确定研究对象初、末状态的机械能(恰当选取参考平面);
4. 根据机械能守恒定律列方程求解。
应用机械能守恒定律解题,只需考虑过程的初、末状态,不必考虑两个状态间过程的细节,这是它的优点。
例4 如图所示,一端与墙相连的水平轻弹簧处于自由伸长状态,质量为4 kg的木块沿光滑的水平面以5 m/s的速度开始运动并挤压弹簧,不计空气阻力,求:
(1)弹簧的最大弹性势能;
(2)木块被弹回速度增大到3 m/s时弹簧的弹性势能。
机械能守恒定律和动能定理的比较:
在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
1、内容:
2、表达式:
3、守恒条件:
只有重力做功或弹力做功,其他力做功为0.
小结
ΔEk=ΔEp
EK2+EP2=EK1+EP1
ΔEA=-ΔEB
此处弹力高中阶段特指弹簧类弹力
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
