3.2 认识万有引力定律(共28张ppt)
文档属性
| 名称 | 3.2 认识万有引力定律(共28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 00:00:00 | ||
图片预览




文档简介
粤教版 必修二 第三章
第三章 万有引力定律
第二节 认识万有引力定律
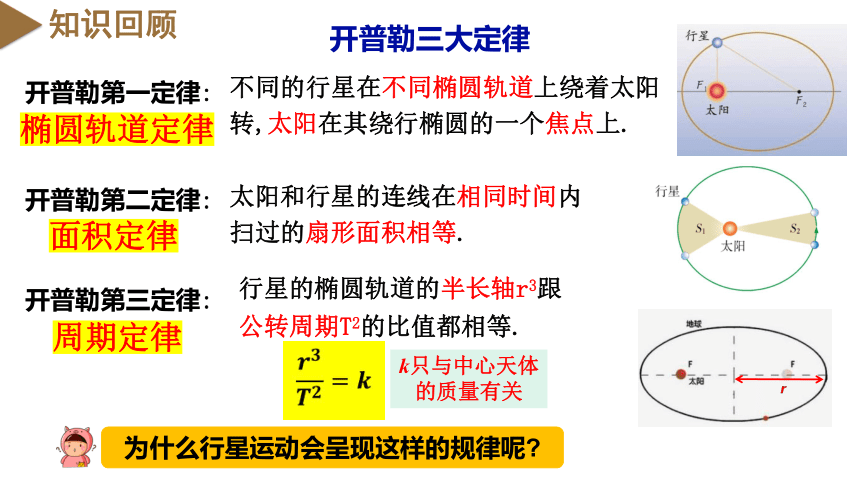
知识回顾
开普勒三大定律
开普勒第一定律:
不同的行星在不同椭圆轨道上绕着太阳转,太阳在其绕行椭圆的一个焦点上.
椭圆轨道定律
开普勒第二定律:
太阳和行星的连线在相同时间内扫过的扇形面积相等.
面积定律
开普勒第三定律:
周期定律
行星的椭圆轨道的半长轴r3跟公转周期T2的比值都相等.
????????????????=????
?
k只与中心天体的质量有关
为什么行星运动会呈现这样的规律呢?
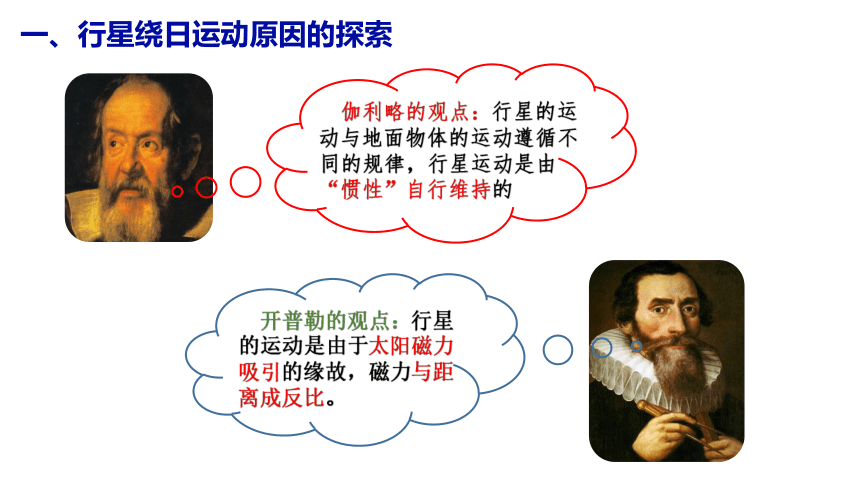
一、行星绕日运动原因的探索
伽利略的观点:行星的运动与地面物体的运动遵循不同的规律,行星运动是由“惯性”自行维持的
开普勒的观点:行星的运动是由于太阳磁力吸引的缘故,磁力与距离成反比。
一、行星绕日运动原因的探索
笛卡尔的观点:太阳的旋涡带动行星和卫星一起运动
胡克的观点:行星的运动是太阳引力的缘故,并且力的大小与到太阳距离的平方成反比。重力是由地球引力引起的
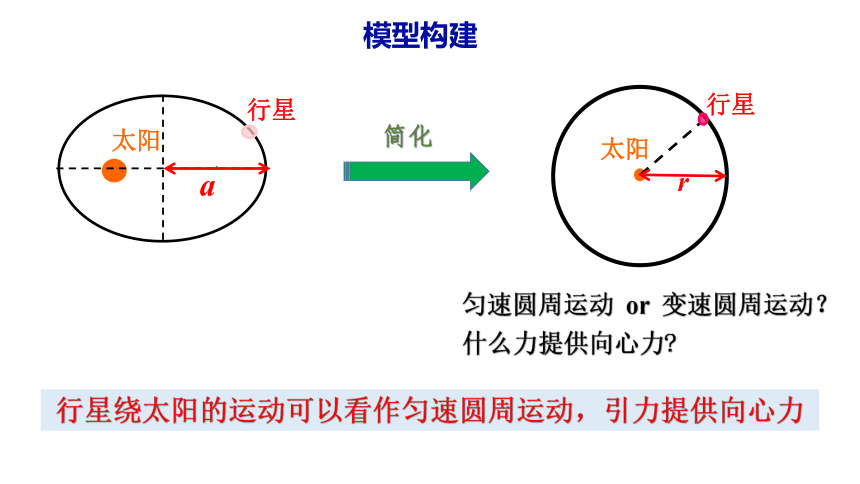
模型构建
简化
太阳
行星
a
太阳
行星
r
匀速圆周运动 or 变速圆周运动?
什么力提供向心力?
行星绕太阳的运动可以看作匀速圆周运动,引力提供向心力
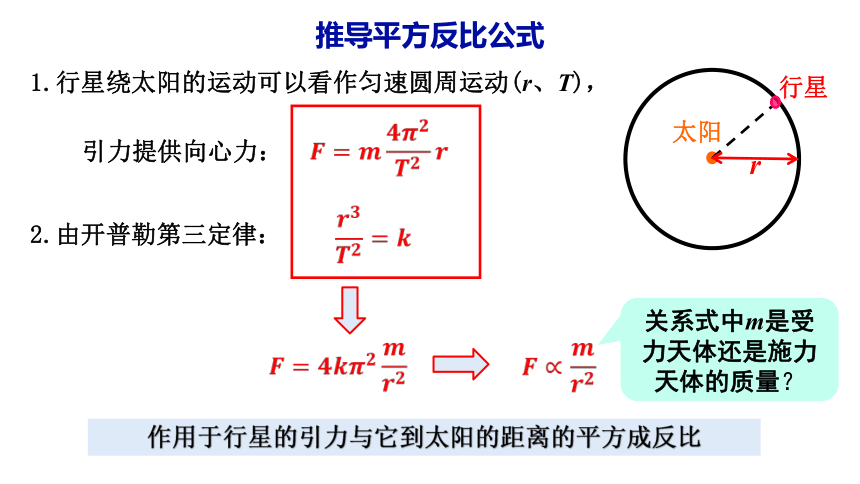
推导平方反比公式
1.行星绕太阳的运动可以看作匀速圆周运动(r、T),
太阳
行星
r
2.由开普勒第三定律:
????????????????=????
?
????=????????????????????????????
?
引力提供向心力:
????=????????????????????????????
?
????∝????????????
?
关系式中m是受力天体还是施力天体的质量?
作用于行星的引力与它到太阳的距离的平方成反比
1684年,哈雷拜访牛顿,征询平方反比定律的轨迹问题。
牛顿回答:轨迹应是椭圆。
同年11月,牛顿给出一篇9页长的论文,论证了在中心吸引力作用下物体的运动轨迹,证明了椭圆轨道运动的平方反比关系
????日对星∝????????????
?
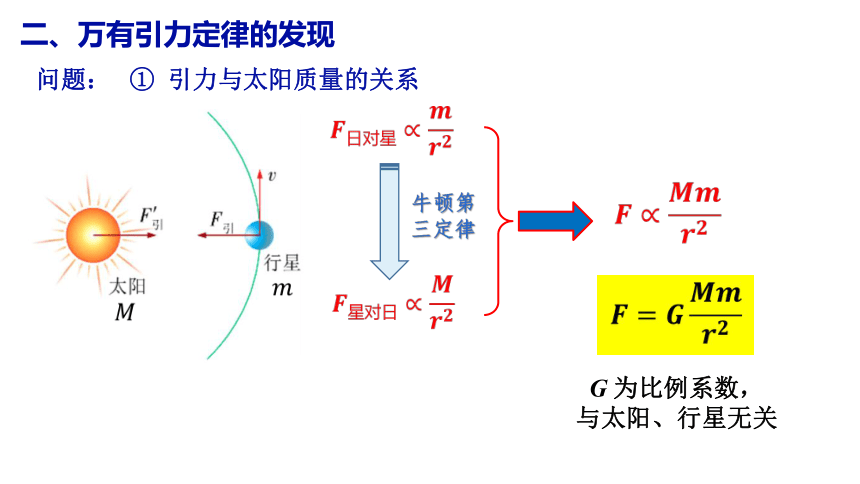
① 引力与太阳质量的关系
② 引力的普遍性
问题:
????日对星∝????????????
?
????
?
????
?
????星对日∝????????????
?
二、万有引力定律的发现
牛顿第三定律
?????∝????????????????
?
?????=????????????????????
?
G 为比例系数,
与太阳、行星无关
① 引力与太阳质量的关系
问题:
二、万有引力定律的发现
② 引力的普遍性
问题:
使苹果落体的重力与地球吸引月球的引力是不是同一种力?
逻辑推理:“平抛石头”思想实验
设想:从山顶水平抛出一块石头。由于重力的作用,石头会沿着弯曲的路径落到地面上,并且石头的抛出速度越大,石头飞行的距离越远。
逻辑推理:当石头抛出的速度足够大时,它会怎么运动?
将绕地球做圆周运动而不再落向地面
月球绕地球运动
猜想:地面上的重力与地吸引月球是同一性质的力
数学演绎推理 —“月地检验”
猜想:地面上的重力与地吸引月球是同一性质的力
牛顿月地检验的基本思路:
假设:维持月球绕地球运动的力及地面物体所受的引力和太阳与行星间的引力都遵循平方反比规律。(已知月球轨道半径是地球半径的60倍 )
地球对地面物体
地球对月球
?????=????????????????????
?
数学演绎推理 —“月地检验”
地面物体
月球
????????向=????2????2=36001
?
思考:如何知道月球的向心加速度呢?
已知:月球的公转周期T=27.3天,月球轨道半径约为地球半径的60倍,地球半径R=6.4×103km,则月球的向心加速度为多少?
数学演绎推理 —“月地检验”
地面物体
月球
????????向=????2????2=36001
?
则在相同的时间内,月球轨道附近自由落体的运动位移是地面附近自由落体的运动位移的 13600
?
根据月球的运行周期、轨道半径,可以算出在较短的时间内月球偏离原速度切线方向的垂直位移y这个位移与在相同时间内月球轨道附近自由落体的运动位移相吻合
二、万有引力定律的发现
② 引力的普遍性
问题:
使苹果落体的重力与地球吸引月球的引力是不是同一种力?
逻辑推理:“平抛石头”思想实验
数学演绎推理 —“月地检验”
结论:使月球绕地球运动的引力以及地面物体所受地球的引力(重力)和太阳与行星之间的力遵循同一规律。
—— 所有行星、所有物体
三、万有引力定律
宇宙间的一切物体都是互相吸引的,两个物体间引力的方向在它们的连线上,引力的大小跟它们的质量的乘积成正比,跟它们的距离的二次方成反比。
2、表达式:
G=6.67×10-11 N.m2/kg2
1、万有引力定律的内容:
3、方向:在两个物体的连线上。
万有引力常量:由英国科学家
卡文迪许利用扭秤实验装置测出
理解1:F=G ????????????????????????
?
公式适用条件:
(1)对于可以看做质点的物体,r为两个质点之间的距离.
m1
m2
r
(2)对于质量分布均匀的球体,r为两个球心之间的距离.
(3)一个均匀球体与球外一个质点,r为球体球心到质点的距离.
理解2:万有引力的四个特性
特性
内容
普遍性
万有引力不仅存在于太阳与行星、地球与月球之间,宇宙间任何两个有质量的物体之间都存在着这种相互吸引的力
相互性
两个有质量的物体之间的万有引力是一对作用力和反作用力,总是满足大小相等,方向相反,作用在两个物体上
宏观性
地面上的物体之间的万有引力一般比较小,与其他力比较可忽略不计,但在质量巨大的天体之间或天体与其附近的物体之间,万有引力起着决定性作用
特殊性
两个物体之间的万有引力只与它们本身的质量和它们间的距离有关,而与它们所在空间的性质无关,也与周围是否存在其他物体无关
思考与讨论
万有引力定律指出,任何物体间都存在着引力。那么,为什么当两个人靠近时,并没有吸引到一起?试估计一下自己和同桌之间的引力有多大.
两人质量均为 60 kg
两人(估算看作质点)相距1m
?????=????????????????????????????
?
=????.????????×?????????????????×????????×????????????????
?
≈????.????×?????????????????
?
一根5cm长的头发,大约0.0005g,重量只有????×?????????????????
?
三、万有引力定律
宇宙间的一切物体都是互相吸引的,两个物体间引力的方向在它们的连线上,引力的大小跟它们的质量的乘积成正比,跟它们的距离的二次方成反比。
2、表达式:
1、万有引力定律的内容:
内容上,万有引力定律适用于一切物体之间
计算时,只适用于质点、质量分布均匀的球体
适用条件:
1. 关于行星对太阳的引力,下列说法正确的是( )
A.行星对太阳的引力提供了行星做匀速圆周运动的向心力
B.行星对太阳的引力大小与行星的质量成正比,与行星和太阳间的距离
成反比
C.太阳对行星的引力公式是由实验得出的
D.太阳对行星的引力公式是由开普勒定律和行星绕太阳做匀速圆周运动
的规律推导出来的
课堂练习
????
?
2. 下列关于万有引力定律的说法中,正确的是( )
①万有引力定律是卡文迪许在实验室中发现的
③对于质量分布均匀的球体,公式中的r是两球心间的距离
④质量大的物体对质量小的物体的引力大于质量小的物体对质量大的物体的引力
A.①③ B.②④ C.②③ D.①④
课堂练习
????
?
3. 如图,两个质量均匀的小球,质量为m,半径为r,两球之间用细杆AB相连,AB长度也为r.某同学认为两球之间的万有引力????=????????????????????.
该同学的看法是否正确?请说明理由.
?
课堂练习
课本P61
4.地球的质量约是月球质量的81倍,若登月飞船通过月地之间的某一个位置时,月球和地球对它的引力大小相等,该位置到月球中心和地球中心的距离之比约为多少
课堂练习
四、万有引力常量G的测定
(1)转换法
将小球和大球之间的万有引力测量转化为对金属丝扭转角度的测量;
又利用横杆与光学仪器,将金属丝扭转角度的测量转化为对光斑在刻度尺上移动距离的测量;
(2)放大法
通过光路放大光斑在刻度尺上移动的距离,以提高测量精度
五、万有引力和重力的关系
1.万有引力是合力
物体受到地球的吸引力为F,
由万有引力公式得F=G ????????????????,方向指向地心O
?
????
?
????
?
2.万有引力有两个分力
除南北两极外,万有引力有两个分力,
一个分力F1提供物体随地球自转的向心力,方向垂直于地轴;另一个分力F2是重力,产生使物体压地面的效果.
一般mg<G ????????????????,重力的方向偏离地心
?
????
?
????
?
五、万有引力和重力的关系
4.重力、重力加速度与高度的关系
(1)地球表面的重力约等于地球的万有引力,
即 mg=G ????????????????,
所以地球表面的重力加速度g=????????????????.
(2)地球上空h高度处,万有引力等于重力,
即 mg=G ????????????+????????,
所以h高度处的重力加速度g=????????????+????????.
?
1.(多选)卡文迪许利用如图所示的扭秤实验装置测量了引力常量G .为了测量石英丝极微小的扭转角,该实验装置中采取的“微小量放大”的主要措施是( )
A.减小石英丝的直径
B.增大T型架横梁的长度
C.利用平面镜对光线的反射
D.增大刻度尺与平面镜的距离
????????
?
2.(多选)已知质量分布均匀的球壳对壳内物体的引力为零.假设沿地轴的方向凿通一条贯穿地球两极的隧道PQ,隧道极窄,地球仍可看作一个球心为O、半径为R、质量分布均匀的球体.以球心O为坐标原点,竖直向下为x轴正方向.从隧道口P点由静止释放一小球,小球能够在隧道PQ内运动,小球运动到某位置时受到的引力大小为F,速度大小为v.小球在运动过程中,下列图像可能正确的是( )
????????
第三章 万有引力定律
第二节 认识万有引力定律
知识回顾
开普勒三大定律
开普勒第一定律:
不同的行星在不同椭圆轨道上绕着太阳转,太阳在其绕行椭圆的一个焦点上.
椭圆轨道定律
开普勒第二定律:
太阳和行星的连线在相同时间内扫过的扇形面积相等.
面积定律
开普勒第三定律:
周期定律
行星的椭圆轨道的半长轴r3跟公转周期T2的比值都相等.
????????????????=????
?
k只与中心天体的质量有关
为什么行星运动会呈现这样的规律呢?
一、行星绕日运动原因的探索
伽利略的观点:行星的运动与地面物体的运动遵循不同的规律,行星运动是由“惯性”自行维持的
开普勒的观点:行星的运动是由于太阳磁力吸引的缘故,磁力与距离成反比。
一、行星绕日运动原因的探索
笛卡尔的观点:太阳的旋涡带动行星和卫星一起运动
胡克的观点:行星的运动是太阳引力的缘故,并且力的大小与到太阳距离的平方成反比。重力是由地球引力引起的
模型构建
简化
太阳
行星
a
太阳
行星
r
匀速圆周运动 or 变速圆周运动?
什么力提供向心力?
行星绕太阳的运动可以看作匀速圆周运动,引力提供向心力
推导平方反比公式
1.行星绕太阳的运动可以看作匀速圆周运动(r、T),
太阳
行星
r
2.由开普勒第三定律:
????????????????=????
?
????=????????????????????????????
?
引力提供向心力:
????=????????????????????????????
?
????∝????????????
?
关系式中m是受力天体还是施力天体的质量?
作用于行星的引力与它到太阳的距离的平方成反比
1684年,哈雷拜访牛顿,征询平方反比定律的轨迹问题。
牛顿回答:轨迹应是椭圆。
同年11月,牛顿给出一篇9页长的论文,论证了在中心吸引力作用下物体的运动轨迹,证明了椭圆轨道运动的平方反比关系
????日对星∝????????????
?
① 引力与太阳质量的关系
② 引力的普遍性
问题:
????日对星∝????????????
?
????
?
????
?
????星对日∝????????????
?
二、万有引力定律的发现
牛顿第三定律
?????∝????????????????
?
?????=????????????????????
?
G 为比例系数,
与太阳、行星无关
① 引力与太阳质量的关系
问题:
二、万有引力定律的发现
② 引力的普遍性
问题:
使苹果落体的重力与地球吸引月球的引力是不是同一种力?
逻辑推理:“平抛石头”思想实验
设想:从山顶水平抛出一块石头。由于重力的作用,石头会沿着弯曲的路径落到地面上,并且石头的抛出速度越大,石头飞行的距离越远。
逻辑推理:当石头抛出的速度足够大时,它会怎么运动?
将绕地球做圆周运动而不再落向地面
月球绕地球运动
猜想:地面上的重力与地吸引月球是同一性质的力
数学演绎推理 —“月地检验”
猜想:地面上的重力与地吸引月球是同一性质的力
牛顿月地检验的基本思路:
假设:维持月球绕地球运动的力及地面物体所受的引力和太阳与行星间的引力都遵循平方反比规律。(已知月球轨道半径是地球半径的60倍 )
地球对地面物体
地球对月球
?????=????????????????????
?
数学演绎推理 —“月地检验”
地面物体
月球
????????向=????2????2=36001
?
思考:如何知道月球的向心加速度呢?
已知:月球的公转周期T=27.3天,月球轨道半径约为地球半径的60倍,地球半径R=6.4×103km,则月球的向心加速度为多少?
数学演绎推理 —“月地检验”
地面物体
月球
????????向=????2????2=36001
?
则在相同的时间内,月球轨道附近自由落体的运动位移是地面附近自由落体的运动位移的 13600
?
根据月球的运行周期、轨道半径,可以算出在较短的时间内月球偏离原速度切线方向的垂直位移y这个位移与在相同时间内月球轨道附近自由落体的运动位移相吻合
二、万有引力定律的发现
② 引力的普遍性
问题:
使苹果落体的重力与地球吸引月球的引力是不是同一种力?
逻辑推理:“平抛石头”思想实验
数学演绎推理 —“月地检验”
结论:使月球绕地球运动的引力以及地面物体所受地球的引力(重力)和太阳与行星之间的力遵循同一规律。
—— 所有行星、所有物体
三、万有引力定律
宇宙间的一切物体都是互相吸引的,两个物体间引力的方向在它们的连线上,引力的大小跟它们的质量的乘积成正比,跟它们的距离的二次方成反比。
2、表达式:
G=6.67×10-11 N.m2/kg2
1、万有引力定律的内容:
3、方向:在两个物体的连线上。
万有引力常量:由英国科学家
卡文迪许利用扭秤实验装置测出
理解1:F=G ????????????????????????
?
公式适用条件:
(1)对于可以看做质点的物体,r为两个质点之间的距离.
m1
m2
r
(2)对于质量分布均匀的球体,r为两个球心之间的距离.
(3)一个均匀球体与球外一个质点,r为球体球心到质点的距离.
理解2:万有引力的四个特性
特性
内容
普遍性
万有引力不仅存在于太阳与行星、地球与月球之间,宇宙间任何两个有质量的物体之间都存在着这种相互吸引的力
相互性
两个有质量的物体之间的万有引力是一对作用力和反作用力,总是满足大小相等,方向相反,作用在两个物体上
宏观性
地面上的物体之间的万有引力一般比较小,与其他力比较可忽略不计,但在质量巨大的天体之间或天体与其附近的物体之间,万有引力起着决定性作用
特殊性
两个物体之间的万有引力只与它们本身的质量和它们间的距离有关,而与它们所在空间的性质无关,也与周围是否存在其他物体无关
思考与讨论
万有引力定律指出,任何物体间都存在着引力。那么,为什么当两个人靠近时,并没有吸引到一起?试估计一下自己和同桌之间的引力有多大.
两人质量均为 60 kg
两人(估算看作质点)相距1m
?????=????????????????????????????
?
=????.????????×?????????????????×????????×????????????????
?
≈????.????×?????????????????
?
一根5cm长的头发,大约0.0005g,重量只有????×?????????????????
?
三、万有引力定律
宇宙间的一切物体都是互相吸引的,两个物体间引力的方向在它们的连线上,引力的大小跟它们的质量的乘积成正比,跟它们的距离的二次方成反比。
2、表达式:
1、万有引力定律的内容:
内容上,万有引力定律适用于一切物体之间
计算时,只适用于质点、质量分布均匀的球体
适用条件:
1. 关于行星对太阳的引力,下列说法正确的是( )
A.行星对太阳的引力提供了行星做匀速圆周运动的向心力
B.行星对太阳的引力大小与行星的质量成正比,与行星和太阳间的距离
成反比
C.太阳对行星的引力公式是由实验得出的
D.太阳对行星的引力公式是由开普勒定律和行星绕太阳做匀速圆周运动
的规律推导出来的
课堂练习
????
?
2. 下列关于万有引力定律的说法中,正确的是( )
①万有引力定律是卡文迪许在实验室中发现的
③对于质量分布均匀的球体,公式中的r是两球心间的距离
④质量大的物体对质量小的物体的引力大于质量小的物体对质量大的物体的引力
A.①③ B.②④ C.②③ D.①④
课堂练习
????
?
3. 如图,两个质量均匀的小球,质量为m,半径为r,两球之间用细杆AB相连,AB长度也为r.某同学认为两球之间的万有引力????=????????????????????.
该同学的看法是否正确?请说明理由.
?
课堂练习
课本P61
4.地球的质量约是月球质量的81倍,若登月飞船通过月地之间的某一个位置时,月球和地球对它的引力大小相等,该位置到月球中心和地球中心的距离之比约为多少
课堂练习
四、万有引力常量G的测定
(1)转换法
将小球和大球之间的万有引力测量转化为对金属丝扭转角度的测量;
又利用横杆与光学仪器,将金属丝扭转角度的测量转化为对光斑在刻度尺上移动距离的测量;
(2)放大法
通过光路放大光斑在刻度尺上移动的距离,以提高测量精度
五、万有引力和重力的关系
1.万有引力是合力
物体受到地球的吸引力为F,
由万有引力公式得F=G ????????????????,方向指向地心O
?
????
?
????
?
2.万有引力有两个分力
除南北两极外,万有引力有两个分力,
一个分力F1提供物体随地球自转的向心力,方向垂直于地轴;另一个分力F2是重力,产生使物体压地面的效果.
一般mg<G ????????????????,重力的方向偏离地心
?
????
?
????
?
五、万有引力和重力的关系
4.重力、重力加速度与高度的关系
(1)地球表面的重力约等于地球的万有引力,
即 mg=G ????????????????,
所以地球表面的重力加速度g=????????????????.
(2)地球上空h高度处,万有引力等于重力,
即 mg=G ????????????+????????,
所以h高度处的重力加速度g=????????????+????????.
?
1.(多选)卡文迪许利用如图所示的扭秤实验装置测量了引力常量G .为了测量石英丝极微小的扭转角,该实验装置中采取的“微小量放大”的主要措施是( )
A.减小石英丝的直径
B.增大T型架横梁的长度
C.利用平面镜对光线的反射
D.增大刻度尺与平面镜的距离
????????
?
2.(多选)已知质量分布均匀的球壳对壳内物体的引力为零.假设沿地轴的方向凿通一条贯穿地球两极的隧道PQ,隧道极窄,地球仍可看作一个球心为O、半径为R、质量分布均匀的球体.以球心O为坐标原点,竖直向下为x轴正方向.从隧道口P点由静止释放一小球,小球能够在隧道PQ内运动,小球运动到某位置时受到的引力大小为F,速度大小为v.小球在运动过程中,下列图像可能正确的是( )
????????
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
