3.3 万有引力定律的应用(共22张ppt)
文档属性
| 名称 | 3.3 万有引力定律的应用(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 23:16:56 | ||
图片预览




文档简介
粤教版 必修二 第三章
第三章 万有引力定律
第三节 万有引力定律的应用
新课导入
一个有趣的现象:
一艘满载5千吨青鱼的渔船,从北极圈附近的挪威人来到非洲赤道附近的一个城市。在货物过磅时,竟发现有19吨青鱼不翼而飞。这条船在航行中从未靠过岸,显然不是失窃所为。这是为什么呢?
新课导入
思考:
1.重力是万有引力吗?
2.二者大小相等吗?
3.可能相等吗?
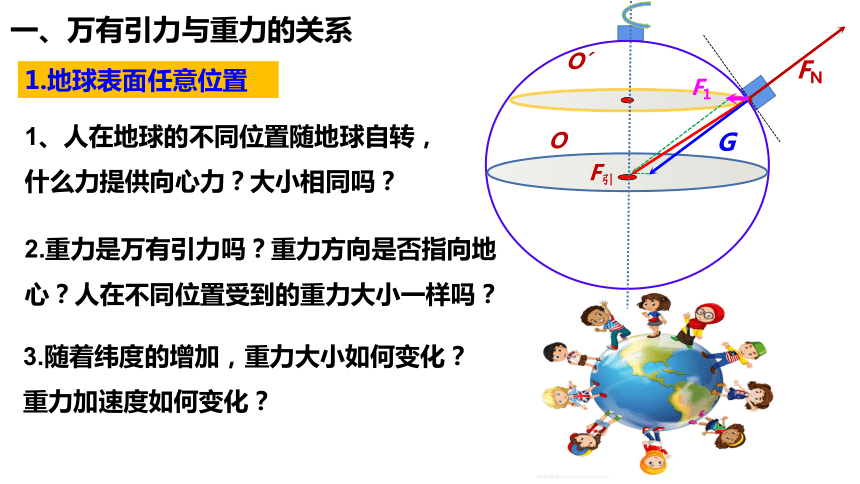
一、万有引力与重力的关系
O
O?
FN
F引
·
F1
G
1、人在地球的不同位置随地球自转,什么力提供向心力?大小相同吗?
2.重力是万有引力吗?重力方向是否指向地心?人在不同位置受到的重力大小一样吗?
3.随着纬度的增加,重力大小如何变化?重力加速度如何变化?
1.地球表面任意位置
O
F引
G
·
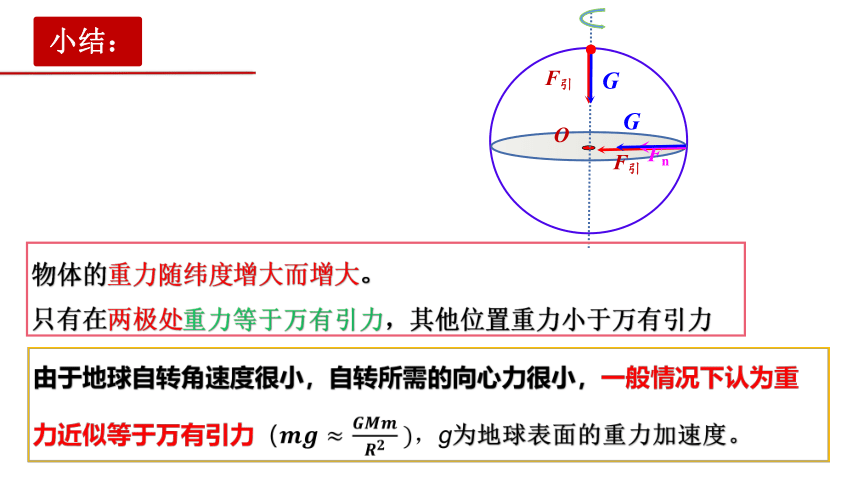
物体的重力随纬度增大而增大。
只有在两极处重力等于万有引力,其他位置重力小于万有引力
Fn
F引
G
小结:
由于地球自转角速度很小,自转所需的向心力很小,一般情况下认为重力近似等于万有引力(????????≈ ?????????????????????),g为地球表面的重力加速度。
?
R
h
F引
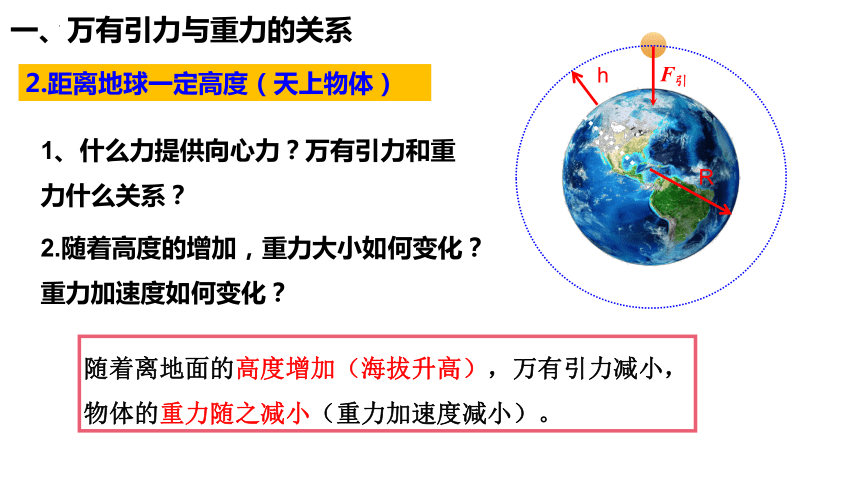
2.距离地球一定高度(天上物体)
1、什么力提供向心力?万有引力和重力什么关系?
2.随着高度的增加,重力大小如何变化?重力加速度如何变化?
随着离地面的高度增加(海拔升高),万有引力减小,物体的重力随之减小(重力加速度减小)。
一、万有引力与重力的关系
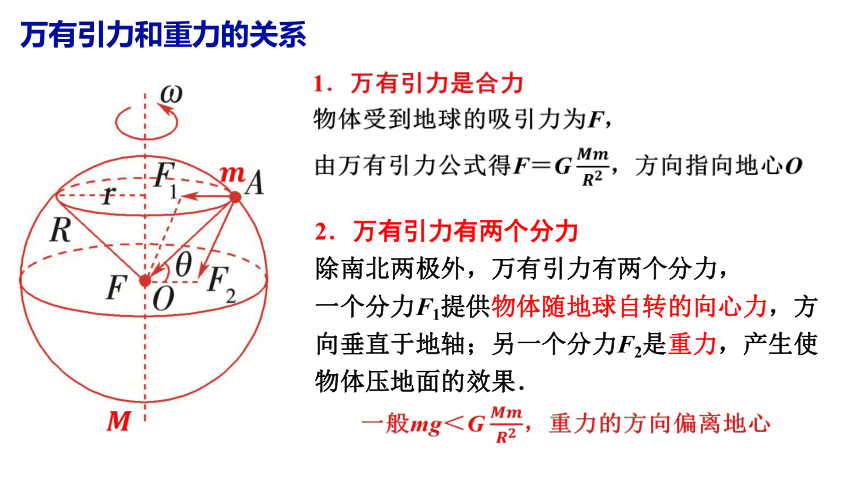
万有引力和重力的关系
1.万有引力是合力
物体受到地球的吸引力为F,
由万有引力公式得F=G ????????????????,方向指向地心O
?
????
?
????
?
2.万有引力有两个分力
除南北两极外,万有引力有两个分力,
一个分力F1提供物体随地球自转的向心力,方向垂直于地轴;另一个分力F2是重力,产生使物体压地面的效果.
一般mg<G ????????????????,重力的方向偏离地心
?
????
?
????
?
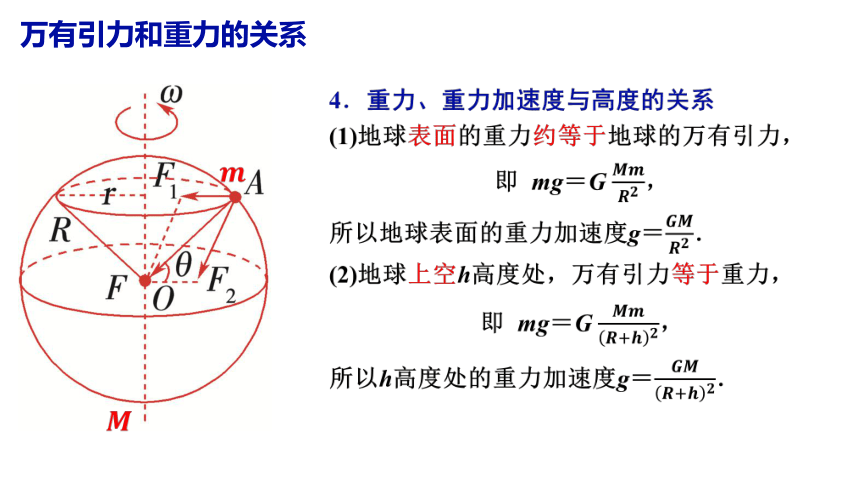
4.重力、重力加速度与高度的关系
(1)地球表面的重力约等于地球的万有引力,
即 mg=G ????????????????,
所以地球表面的重力加速度g=????????????????.
(2)地球上空h高度处,万有引力等于重力,
即 mg=G ????????????+????????,
所以h高度处的重力加速度g=????????????+????????.
?
万有引力和重力的关系
例1
地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
A. 物体在赤道处受到的地球引力等于两极处,而重力小于两极处
B. 赤道处的角速度比南纬30°大
C. 地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度
比两极处大
D. 地面上的物体随地球自转时提供向心力的是重力
????
?
例2 (多选)假如地球自转速度增大,关于物体的重力,
下列说法中正确的是( )
A.放在赤道地面上物体的万有引力不变
B.放在两极地面上物体的重力不变
C.放在赤道地面上物体的重力减小
D.放在两极地面上物体的重力增大
ABC
例3 假设地球可视为质量均匀分布的球体,已知地球表面的重力加速度在两极的大小为g0,在赤道的大小为g;地球自转的周期为T,引力常量为G,则地球的半径为( )
A. (?????????????)???????????????????? B. (????????+????)???????????????????? C. ???????????????????????????? D. ????????????????????????
?
????
?
例4 我国“嫦娥四号”探测器成功在月球背面软着陆.在探测器“奔向”月球的过程中,用h表示探测器与地球表面的距离,F表示它所受的地球引力,能够描述F随h变化关系的图像是( )
????
?
A. B. C. D.
例5
????
?
例6 据报道,科学家们在太阳系外发现了一颗“宜居”行星,其质量约为地球质量的6.4倍.已知一个在地球表面质量为50 kg的人在这个行星表面的重量约为800 N,地球表面处的重力加速度为10 m/s2.求:
(1)该行星表面处的重力加速度.
(2)该行星的半径与地球的半径之比约为多少?
(3)若在该行星上距行星表面8 m高处,以10 m/s的水平初速度抛出一个小球(不计任何阻力),则小球的水平射程是多大?
思考:
1.生活中的物体的质量我们可以通过天平来测量,对于地球,我们又用什么方法来“称量”其质量呢?
2.若已知地球表面重力加速度g,地球半径R,引力常量G,求地球的质量和密度?
3.如果知道月球绕地球的公转周期T,月球与地球中心间距r,引力常量G,求地球的质量与密度?
4.根据题中所给的已知条件,能否求出月球的质量?
二、天体质量、密度的测量
物体在天体表面时受到的重力等于万有引力
g: 天体表面的重力加速度
R: 天体的半径
计算中心天体质量———“表面”法
行星(或卫星)做匀速圆周运动 F万=F向
只能求出中心天体的质量!!!
得,
计算天体质量———“环绕”法
例1 (多选)一卫星绕地球做匀速圆周运动,其轨道半径为r,卫星绕地球做匀速圆周运动的周期为T,已知地球的半径为R,地球表面的重力加速度为g,引力常量为G,则地球的质量可表示为( )
????????
?
例2 (多选)已知下列哪组数据,可以算出地球的质量M( )
A.月球绕地球运动的周期T1及月球到地球中心的距离R1
B.地球绕太阳运行的周期T2及地球到太阳中心的距离R2
C.人造地球卫星在地面附近的运行速度v3和运行周期T3
D.地球绕太阳运行的速度v4及地球到太阳中心的距离R4
????????
?
例3 航天员在某一星球距离星球表面h高度处,以初速度v0沿水平方向抛出一个小球,经过时间t后小球落到该星球表面,已知该星球的半径为R(R?h),引力常量为G,则该星球的质量为( )
A.???????????????????????????? B.???????????????????????? C.???????????????????????? D.????????????????????????????
?
????
?
练习1 为进一步获取月球的相关数据,我国成功地进行了“嫦娥五号”的发射.该卫星在月球上空绕月球做匀速圆周运动时,经过时间t,卫星运动的路程为s,卫星与月球中心连线扫过的角度是θ(弧度),引力常量为G ,月球半径为R,则可推知月球的密度是( )
B
练习2 假设在半径为R的某天体上发射一颗该天体的卫星,已知引力常量为G,忽略该天体自转。
(1)若卫星距该天体表面的高度为h,测得卫星在该处做圆周运动的周期为T1,则该天体的质量、密度是多少?
(2)若卫星贴近该天体的表面做匀速圆周运动的周期为T2,则该天体的质量、密度是多少?
第三章 万有引力定律
第三节 万有引力定律的应用
新课导入
一个有趣的现象:
一艘满载5千吨青鱼的渔船,从北极圈附近的挪威人来到非洲赤道附近的一个城市。在货物过磅时,竟发现有19吨青鱼不翼而飞。这条船在航行中从未靠过岸,显然不是失窃所为。这是为什么呢?
新课导入
思考:
1.重力是万有引力吗?
2.二者大小相等吗?
3.可能相等吗?
一、万有引力与重力的关系
O
O?
FN
F引
·
F1
G
1、人在地球的不同位置随地球自转,什么力提供向心力?大小相同吗?
2.重力是万有引力吗?重力方向是否指向地心?人在不同位置受到的重力大小一样吗?
3.随着纬度的增加,重力大小如何变化?重力加速度如何变化?
1.地球表面任意位置
O
F引
G
·
物体的重力随纬度增大而增大。
只有在两极处重力等于万有引力,其他位置重力小于万有引力
Fn
F引
G
小结:
由于地球自转角速度很小,自转所需的向心力很小,一般情况下认为重力近似等于万有引力(????????≈ ?????????????????????),g为地球表面的重力加速度。
?
R
h
F引
2.距离地球一定高度(天上物体)
1、什么力提供向心力?万有引力和重力什么关系?
2.随着高度的增加,重力大小如何变化?重力加速度如何变化?
随着离地面的高度增加(海拔升高),万有引力减小,物体的重力随之减小(重力加速度减小)。
一、万有引力与重力的关系
万有引力和重力的关系
1.万有引力是合力
物体受到地球的吸引力为F,
由万有引力公式得F=G ????????????????,方向指向地心O
?
????
?
????
?
2.万有引力有两个分力
除南北两极外,万有引力有两个分力,
一个分力F1提供物体随地球自转的向心力,方向垂直于地轴;另一个分力F2是重力,产生使物体压地面的效果.
一般mg<G ????????????????,重力的方向偏离地心
?
????
?
????
?
4.重力、重力加速度与高度的关系
(1)地球表面的重力约等于地球的万有引力,
即 mg=G ????????????????,
所以地球表面的重力加速度g=????????????????.
(2)地球上空h高度处,万有引力等于重力,
即 mg=G ????????????+????????,
所以h高度处的重力加速度g=????????????+????????.
?
万有引力和重力的关系
例1
地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
A. 物体在赤道处受到的地球引力等于两极处,而重力小于两极处
B. 赤道处的角速度比南纬30°大
C. 地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度
比两极处大
D. 地面上的物体随地球自转时提供向心力的是重力
????
?
例2 (多选)假如地球自转速度增大,关于物体的重力,
下列说法中正确的是( )
A.放在赤道地面上物体的万有引力不变
B.放在两极地面上物体的重力不变
C.放在赤道地面上物体的重力减小
D.放在两极地面上物体的重力增大
ABC
例3 假设地球可视为质量均匀分布的球体,已知地球表面的重力加速度在两极的大小为g0,在赤道的大小为g;地球自转的周期为T,引力常量为G,则地球的半径为( )
A. (?????????????)???????????????????? B. (????????+????)???????????????????? C. ???????????????????????????? D. ????????????????????????
?
????
?
例4 我国“嫦娥四号”探测器成功在月球背面软着陆.在探测器“奔向”月球的过程中,用h表示探测器与地球表面的距离,F表示它所受的地球引力,能够描述F随h变化关系的图像是( )
????
?
A. B. C. D.
例5
????
?
例6 据报道,科学家们在太阳系外发现了一颗“宜居”行星,其质量约为地球质量的6.4倍.已知一个在地球表面质量为50 kg的人在这个行星表面的重量约为800 N,地球表面处的重力加速度为10 m/s2.求:
(1)该行星表面处的重力加速度.
(2)该行星的半径与地球的半径之比约为多少?
(3)若在该行星上距行星表面8 m高处,以10 m/s的水平初速度抛出一个小球(不计任何阻力),则小球的水平射程是多大?
思考:
1.生活中的物体的质量我们可以通过天平来测量,对于地球,我们又用什么方法来“称量”其质量呢?
2.若已知地球表面重力加速度g,地球半径R,引力常量G,求地球的质量和密度?
3.如果知道月球绕地球的公转周期T,月球与地球中心间距r,引力常量G,求地球的质量与密度?
4.根据题中所给的已知条件,能否求出月球的质量?
二、天体质量、密度的测量
物体在天体表面时受到的重力等于万有引力
g: 天体表面的重力加速度
R: 天体的半径
计算中心天体质量———“表面”法
行星(或卫星)做匀速圆周运动 F万=F向
只能求出中心天体的质量!!!
得,
计算天体质量———“环绕”法
例1 (多选)一卫星绕地球做匀速圆周运动,其轨道半径为r,卫星绕地球做匀速圆周运动的周期为T,已知地球的半径为R,地球表面的重力加速度为g,引力常量为G,则地球的质量可表示为( )
????????
?
例2 (多选)已知下列哪组数据,可以算出地球的质量M( )
A.月球绕地球运动的周期T1及月球到地球中心的距离R1
B.地球绕太阳运行的周期T2及地球到太阳中心的距离R2
C.人造地球卫星在地面附近的运行速度v3和运行周期T3
D.地球绕太阳运行的速度v4及地球到太阳中心的距离R4
????????
?
例3 航天员在某一星球距离星球表面h高度处,以初速度v0沿水平方向抛出一个小球,经过时间t后小球落到该星球表面,已知该星球的半径为R(R?h),引力常量为G,则该星球的质量为( )
A.???????????????????????????? B.???????????????????????? C.???????????????????????? D.????????????????????????????
?
????
?
练习1 为进一步获取月球的相关数据,我国成功地进行了“嫦娥五号”的发射.该卫星在月球上空绕月球做匀速圆周运动时,经过时间t,卫星运动的路程为s,卫星与月球中心连线扫过的角度是θ(弧度),引力常量为G ,月球半径为R,则可推知月球的密度是( )
B
练习2 假设在半径为R的某天体上发射一颗该天体的卫星,已知引力常量为G,忽略该天体自转。
(1)若卫星距该天体表面的高度为h,测得卫星在该处做圆周运动的周期为T1,则该天体的质量、密度是多少?
(2)若卫星贴近该天体的表面做匀速圆周运动的周期为T2,则该天体的质量、密度是多少?
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
