4.1.2 变力做功(共16张ppt)
文档属性
| 名称 | 4.1.2 变力做功(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-01 23:24:57 | ||
图片预览




文档简介
(共16张PPT)
粤教版 必修二 第四章
第四章 机械能及守恒定律
4.1.2 变力做功
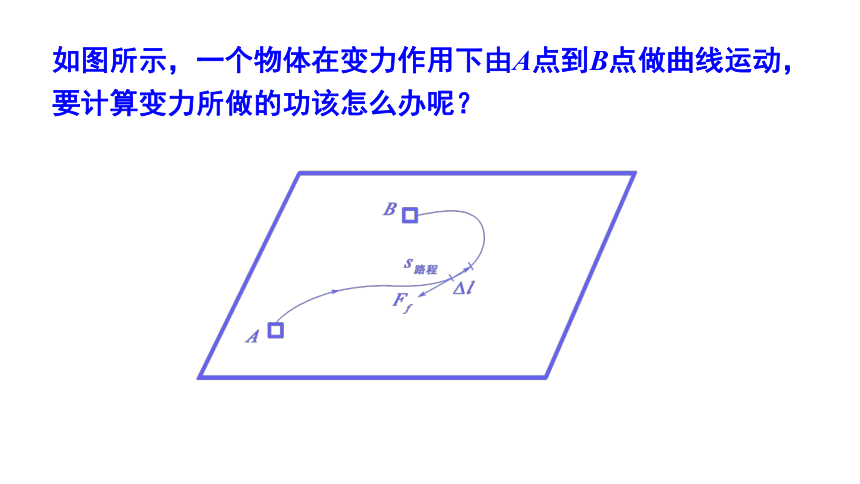
如图所示,一个物体在变力作用下由A点到B点做曲线运动,要计算变力所做的功该怎么办呢?
【典例】质量为m的物体以一定的初速度滑上斜面(斜面足够长),上滑到最高点后又沿原路返回。已知斜面倾角为θ ,物体与斜面的动摩擦因数为μ,上滑的最大高度为h。则物体从开始滑上斜面到滑回到出发点的过程中,重力、摩擦力各做了多少功?
变力做功
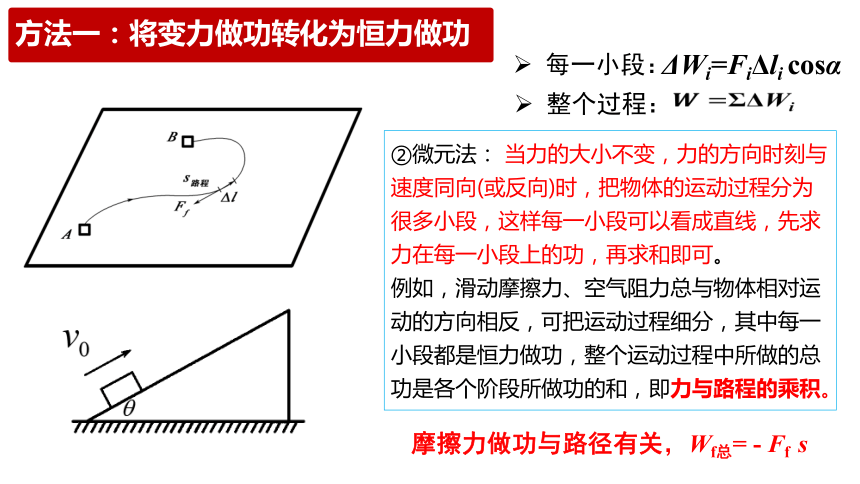
方法一:将变力做功转化为恒力做功
①分段法:
力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段的功,再利用求和的方法计算整个过程中变力做的功。
方法一:将变力做功转化为恒力做功
②微元法: 当力的大小不变,力的方向时刻与速度同向(或反向)时,把物体的运动过程分为很多小段,这样每一小段可以看成直线,先求力在每一小段上的功,再求和即可。
例如,滑动摩擦力、空气阻力总与物体相对运动的方向相反,可把运动过程细分,其中每一小段都是恒力做功,整个运动过程中所做的总功是各个阶段所做功的和,即力与路程的乘积。
摩擦力做功与路径有关,Wf总= - Ff s
每一小段:
整个过程:
ΣΔWi
ΔWi=FiΔli cosα
【例2】如图所示,质量为m的质点在水平面上半径为R的圆槽运动一周.
已知动摩擦因数为μ,求摩擦力对质点做的功.
【例1】质量为m的物体以一定的初速度滑上斜面(斜面足够长),上滑到最高点后又沿原路返回。已知斜面倾角为θ ,物体与斜面的动摩擦因数为μ,上滑的最大高度为h。则物体从开始滑上斜面到滑回到出发点的过程中,重力、摩擦力各做了多少功?
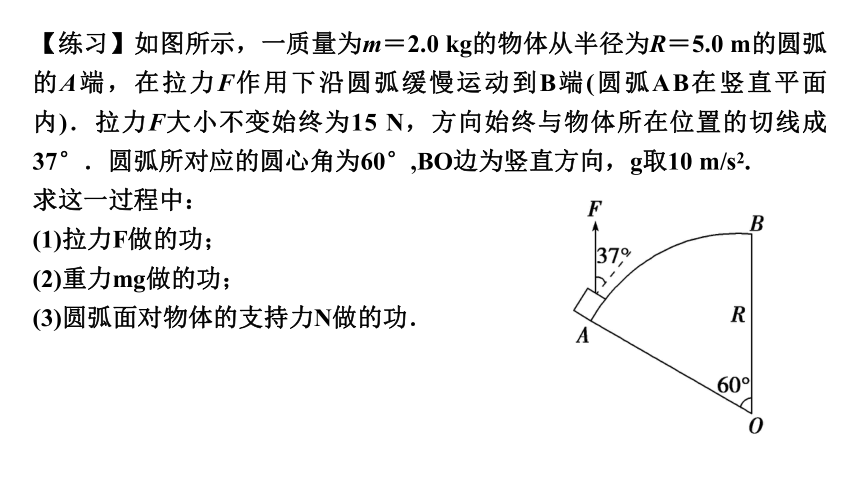
【练习】如图所示,一质量为m=2.0 kg的物体从半径为R=5.0 m的圆弧的A端,在拉力F作用下沿圆弧缓慢运动到B端(圆弧AB在竖直平面内).拉力F大小不变始终为15 N,方向始终与物体所在位置的切线成37°.圆弧所对应的圆心角为60°,BO边为竖直方向,g取10 m/s2.
求这一过程中:
(1)拉力F做的功;
(2)重力mg做的功;
(3)圆弧面对物体的支持力N做的功.
变力做功
方法二:图像法
F/N
O
x
l
F
W=Fl
思考:F-l 图像的面积是否有意义?
v0
v
O
t
t
v4
t1
t2
t3
t4
v3
v2
v1
匀变速直线运动的位移与速度的关系
类比:
v
O
t
t
v
图像法
变力做功
F/N
O
x
l
F
F-l 图像的面积:力F 做的功
位于x轴上方的“面积”为正功
位于x轴下方的“面积”为负功
方法二:图像法
【例3】一物体所受的力F随位移s变化的图像如图所示,在这一过程中,力F对物体做的功为( )
A. 3 J B. 6 J C. 7 J D. 8 J
变式:如图甲所示,静置于光滑水平面上坐标原点处的小物块,在水平拉力F的作用下,沿x轴正方向运动,拉力F随物块所在位置坐标x的变化关系如图乙所示,图线为半圆.则小物块运动到x0处时拉力F 做的功为( )
C
方法三:平均值法
F
O
x
l1
l2
F2
F1
W= l2-l1)
当力的方向不变,大小随位移按线性规律变化时,可先求出力对位移的平均值 ,再由W= Fxcos α计算功
【例4】 用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比。已知铁锤第一次将钉子钉进的深度为1cm,如果铁锤继续钉钉子时对钉子做的功与第一次相同,则第二次钉子进入木板的深度是?
第三次钉子进入木板的深度是?
答案:
方法四:等效转化法
【例5】如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功.
h
A
B
【变式】人在A点拉着绳通过一个光滑定滑轮以加速度a匀加速吊起质量为m的物体,如图所示,保持人手与滑轮间的距离不变,大小为h,开始时绳与水平方向成 600 角,当人拉着绳由A点沿水平方向运动到B点时,绳与水平方向成300 角,求人对绳的拉力做了多少功?(不计摩擦)
h
粤教版 必修二 第四章
第四章 机械能及守恒定律
4.1.2 变力做功
如图所示,一个物体在变力作用下由A点到B点做曲线运动,要计算变力所做的功该怎么办呢?
【典例】质量为m的物体以一定的初速度滑上斜面(斜面足够长),上滑到最高点后又沿原路返回。已知斜面倾角为θ ,物体与斜面的动摩擦因数为μ,上滑的最大高度为h。则物体从开始滑上斜面到滑回到出发点的过程中,重力、摩擦力各做了多少功?
变力做功
方法一:将变力做功转化为恒力做功
①分段法:
力在全程是变力,但在每一个阶段是恒力,这样就可以先计算每个阶段的功,再利用求和的方法计算整个过程中变力做的功。
方法一:将变力做功转化为恒力做功
②微元法: 当力的大小不变,力的方向时刻与速度同向(或反向)时,把物体的运动过程分为很多小段,这样每一小段可以看成直线,先求力在每一小段上的功,再求和即可。
例如,滑动摩擦力、空气阻力总与物体相对运动的方向相反,可把运动过程细分,其中每一小段都是恒力做功,整个运动过程中所做的总功是各个阶段所做功的和,即力与路程的乘积。
摩擦力做功与路径有关,Wf总= - Ff s
每一小段:
整个过程:
ΣΔWi
ΔWi=FiΔli cosα
【例2】如图所示,质量为m的质点在水平面上半径为R的圆槽运动一周.
已知动摩擦因数为μ,求摩擦力对质点做的功.
【例1】质量为m的物体以一定的初速度滑上斜面(斜面足够长),上滑到最高点后又沿原路返回。已知斜面倾角为θ ,物体与斜面的动摩擦因数为μ,上滑的最大高度为h。则物体从开始滑上斜面到滑回到出发点的过程中,重力、摩擦力各做了多少功?
【练习】如图所示,一质量为m=2.0 kg的物体从半径为R=5.0 m的圆弧的A端,在拉力F作用下沿圆弧缓慢运动到B端(圆弧AB在竖直平面内).拉力F大小不变始终为15 N,方向始终与物体所在位置的切线成37°.圆弧所对应的圆心角为60°,BO边为竖直方向,g取10 m/s2.
求这一过程中:
(1)拉力F做的功;
(2)重力mg做的功;
(3)圆弧面对物体的支持力N做的功.
变力做功
方法二:图像法
F/N
O
x
l
F
W=Fl
思考:F-l 图像的面积是否有意义?
v0
v
O
t
t
v4
t1
t2
t3
t4
v3
v2
v1
匀变速直线运动的位移与速度的关系
类比:
v
O
t
t
v
图像法
变力做功
F/N
O
x
l
F
F-l 图像的面积:力F 做的功
位于x轴上方的“面积”为正功
位于x轴下方的“面积”为负功
方法二:图像法
【例3】一物体所受的力F随位移s变化的图像如图所示,在这一过程中,力F对物体做的功为( )
A. 3 J B. 6 J C. 7 J D. 8 J
变式:如图甲所示,静置于光滑水平面上坐标原点处的小物块,在水平拉力F的作用下,沿x轴正方向运动,拉力F随物块所在位置坐标x的变化关系如图乙所示,图线为半圆.则小物块运动到x0处时拉力F 做的功为( )
C
方法三:平均值法
F
O
x
l1
l2
F2
F1
W= l2-l1)
当力的方向不变,大小随位移按线性规律变化时,可先求出力对位移的平均值 ,再由W= Fxcos α计算功
【例4】 用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比。已知铁锤第一次将钉子钉进的深度为1cm,如果铁锤继续钉钉子时对钉子做的功与第一次相同,则第二次钉子进入木板的深度是?
第三次钉子进入木板的深度是?
答案:
方法四:等效转化法
【例5】如图,用恒力F通过跨过光滑定滑轮的轻绳,将静止于水平面上的物体从位置A拉到位置B,物体和滑轮的大小均忽略,定滑轮距水平面高为h,物体在位置A、B时,细绳与水平面的夹角分别为α和β,求绳的拉力F对物体做的功.
h
A
B
【变式】人在A点拉着绳通过一个光滑定滑轮以加速度a匀加速吊起质量为m的物体,如图所示,保持人手与滑轮间的距离不变,大小为h,开始时绳与水平方向成 600 角,当人拉着绳由A点沿水平方向运动到B点时,绳与水平方向成300 角,求人对绳的拉力做了多少功?(不计摩擦)
h
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
