2026届高考数学一轮模拟测试卷三(全国甲卷)(含答案)
文档属性
| 名称 | 2026届高考数学一轮模拟测试卷三(全国甲卷)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 760.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 09:49:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2026届高考数学一轮模拟测试卷三(全国甲卷)
一、选择题
1.(2025·广东模拟)复数( )
A. B. C. D.
2.(2025·浙江模拟)已知,,且,则( )
A.4 B.2 C. D.1
3.(2025·阳西模拟)若集合,则( )
A. B.
C. D.
4.(2025·阳西模拟)投篮测试中,每人投2次,至少投中1次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
A.0.24 B.0.48 C.0.84 D.0.94
5.(2025·四川模拟)已知圆上恰有两个点到直线的距离为2,则m的取值范围是( )
A. B.
C. D.
6.(2025·揭阳模拟)“物竞天择,适者生存”是大自然环境下选择的结果,森林中某些昆虫会通过向后跳跃的方式来躲避偷袭的天敌.经某生物小组研究表明某类昆虫在水平速度为v(单位:分米/秒)时的跳跃高度H(单位:米)近似满足的等量关系,则该类昆虫的最大跳跃高度约为( )
A.米 B.米 C.米 D.米
7.(2025·雅安模拟)已知正四棱锥的所有顶点都在同一个球面上,若该棱锥的高为1,底面边长为2,则球的体积为( )
A. B. C. D.
8.(2025·威海模拟)已知双曲线的左、右焦点分别为,过的直线与的右支交于两点,若,则的离心率为( )
A. B. C.2 D.
二、多项选择题
9.(2025·浙江模拟)已知,,则下列说法正确的是( )
A.若,则
B.的最小值为1
C.若,则的最小值为8
D.若恒成立,则的最小值为
10.(2025·浙江模拟)已知函数(其中,)的最大值为,其图象的相邻两条对称轴之间的距离为,则下列说法正确的是( )
A.
B.函数的图象向左平移单位后关于原点对称
C.函数的图象关于点对称
D.函数在区间上单调递增
11.(2025·阳西模拟)已知球O是棱长为2的正方体的外接球,为球O的直径,点P为该正方体表面上的一动点,则下列说法中正确的是( )
A.当P为中点时,直线与所成角的余弦值为
B.当三棱锥的体积为时,点P轨迹的长度为2
C.的最小值为
D.的最大值为
三、填空题
12.(2025·浙江模拟)已知的展开式中含项的系数为16,则 .
13.(2025·张掖模拟)已知等比数列的前项积为,若,则 .
14.(2025·北京市模拟)已知直线和曲线,给出下列四个结论:
①存在实数和,使直线和曲线没有交点;
②存在实数,对任意实数,直线和曲线恰有个交点;
③存在实数,对任意实数,直线和曲线不会恰有个交点;
④对任意实数和,直线和曲线不会恰有个交点.
其中所有正确结论的序号是 .
四、解答题
15.(2025·上海市模拟)在中,角,,所对边的边长分别为,,,且满足
(1)求角的值;
(2)若,求周长的最大值.
16.(2025·上海市模拟)如图,为圆锥的顶点,是圆锥底面的圆心,,是底面半径,,为劣弧的中点.
(1)证明:平面;
(2)若圆锥底面半径为1,高为2,求平面与平面所成锐二面角的余弦值.
17.(2025·天河模拟)为减少环境污染,保护生态环境,某校进行了“垃圾分类知识普及活动”,并对高一、高二全体学生进行了相关知识测试.现从高一、高二各随机抽取了20名学生,对他们的成绩(百分制)进行了整理和分析后得到如下信息:
高一年级成绩分布表
成绩
人数 1 2 3 4 10
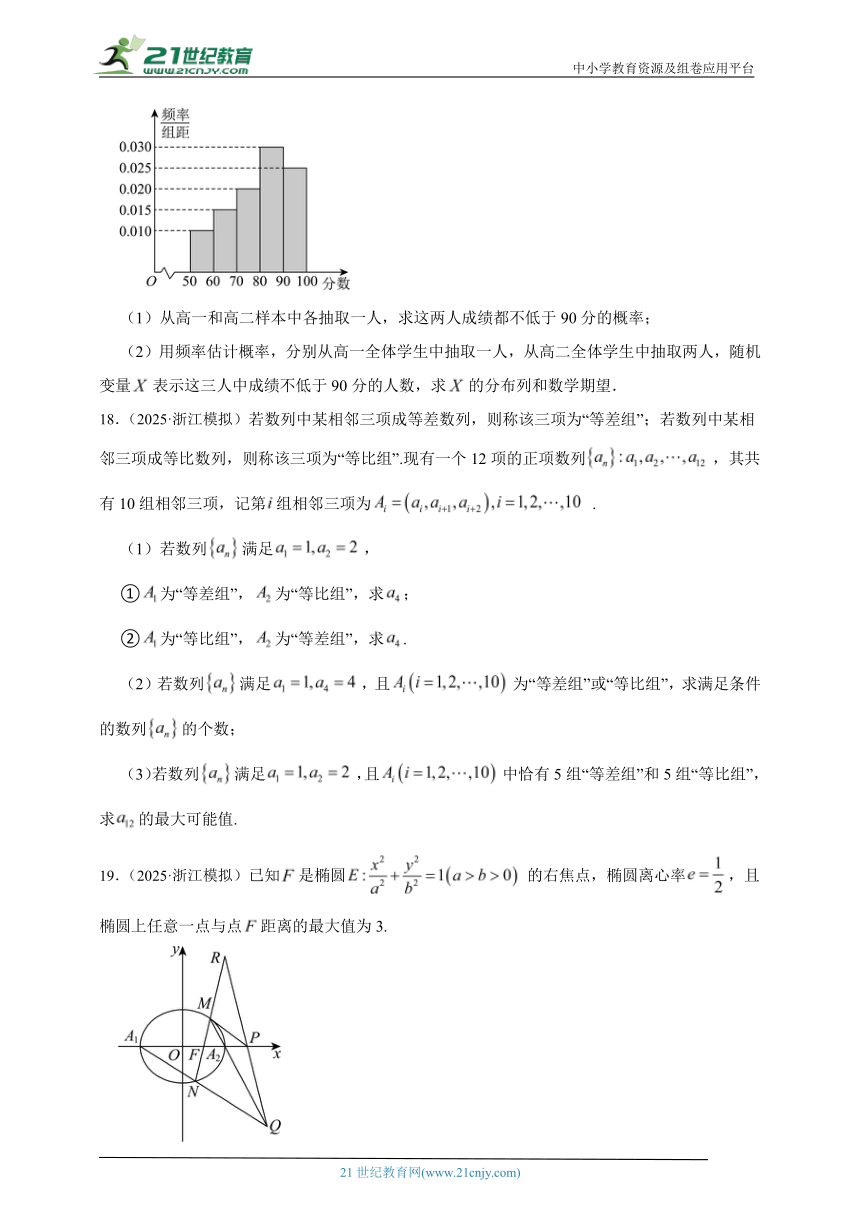
高二年级成绩频率分布直方图
(1)从高一和高二样本中各抽取一人,求这两人成绩都不低于90分的概率;
(2)用频率估计概率,分别从高一全体学生中抽取一人,从高二全体学生中抽取两人,随机变量表示这三人中成绩不低于90分的人数,求的分布列和数学期望.
18.(2025·浙江模拟)若数列中某相邻三项成等差数列,则称该三项为“等差组”;若数列中某相邻三项成等比数列,则称该三项为“等比组”.现有一个12项的正项数列,其共有10组相邻三项,记第组相邻三项为.
(1)若数列满足,
①为“等差组”,为“等比组”,求;
②为“等比组”,为“等差组”,求.
(2)若数列满足,且为“等差组”或“等比组”,求满足条件的数列的个数;
(3)若数列满足,且中恰有5组“等差组”和5组“等比组”,求的最大可能值.
19.(2025·浙江模拟)已知是椭圆的右焦点,椭圆离心率,且椭圆上任意一点与点距离的最大值为3.
(1)求椭圆的方程;
(2)点在椭圆上,椭圆在点处的切线交轴于点.
①求的最小值;
②设分别为椭圆的左 右顶点,不垂直轴的直线交椭圆于另一点,直线与直线交于点,问直线与直线的交点是否在一条定直线上?若是,求出该直线方程;若不是,请说明理由.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】A,C
10.【答案】A,B,D
11.【答案】A,C,D
12.【答案】2
13.【答案】1
14.【答案】①②③
15.【答案】(1)解:由正弦定理可得,即
由余弦定理可得,
因为所以
(2)解:由余弦定理可知, ,所以
所以
所以,当且仅当时,等号成立,
所以
所以三角形的周长的最大值为
16.【答案】(1)证明:如图所示,连接,
因为点是劣弧的中点,,
所以.
因为,所以为等边三角形.
所以,所以,
因为平面,不在平面上,
所以平面.
(2)解:如图所示,过点作交于点,以,,所在直线分别为轴,轴,轴建立空间直角坐标系
所以、、、,
所以,,,
设平面的一个法向量为,
所以,令,则x1=4,y1=0,
所以,
设平面的一个法向量为,
所以,令,则,,
所以,
所以,
所以平面与平面所成锐二面角的余弦值为.
17.【答案】(1)解:由题意可知:高一年级成绩成绩不低于90分的概率为;
高二年级成绩不低于90分的概率为,
则从高一和高二样本中各抽取1人,这两人的成绩都不低于90分的概率为:;
(2)解:由题意可知,随机变量的可能取值为0,1,2,3,
,
,
,
,
的分布列为:
0 1 2 3
.
18.【答案】(1)①因为为“等差组”,故成等差数列,故,故,而为“等比组”,故成等比数列,故,故.
②若为“等比组”,为“等差组”,则成等比数列,故,
且成等差数列,故.
(2)因为为“等差组”或“等比组”,故有4种情形:若为“等差组”,为“等差组”,则;
若为“等差组”,为“等比组”,则,
而为正项数列,故即,
故,而,故,故,;
若为“等比组”,为“等比组”,则,;
若为“等比组”,为“等差组”,则,
故,而,故,.
从而开始的相邻三项,要么为“等比组”,要么为“等差组”,
对于确定的、,此后等比组的公比、等差组的公差均确定,
故此时有个满足条件的数列,
故满足条件的数列的个数为.
(3)先考虑一个一般命题:若,若正项数列中中一个“等差组”,另一个为“等比组”,则先“等比组”再“等差组”得到的较大.
证明:若先“等差组”,再“等比组”,则,
若先“等比组”,再“等差组”,则,其中,
此时
,
故先“等比组”再“等差组”得到的较大..
再考虑另一个一般命题:若,若正项数列中的为“等差组”或“等比组”,则当增大时,也增大.
证明:若均为“等差组”或“等比组”,
由等差数列的性质和等比数列的性质可得当增大时,也增大.
若先“等差组”,再“等比组”,则,
由得,
故由双勾函数的性质可得增大时,也增大;
若先“等比组”,再“等差组”,则,
而,故增大时,也增大,故命题成立.
对于数列满足,,
而中恰有5组“等差组”和5组“等比组”,
要使得的最大,则前述两个命题可得需前5组为“等比组”,
后5组为“等差组”,此时个数分别为,
故的最大可能值为.
19.【答案】(1)由已知,解得,
所以,所以椭圆方程为;
(2)由已知,解得,
所以,所以椭圆方程为;
(2)
①因为切线交轴于点,所以,,
因为点在椭圆上,所以,即,
又,
因为,所以,所以,
所以,
所以,
当且仅当,即时等号成立,所以的最小值为;
②由已知设直线:,,
由消元得,
则,,
所以,
因为,,所以,
因为,,所以,
所以
,
即点,所以直线的方程为,
与直线联立,得,
因为,所以,代入上式可得
,
即,解得,
即点在直线上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2026届高考数学一轮模拟测试卷三(全国甲卷)
一、选择题
1.(2025·广东模拟)复数( )
A. B. C. D.
2.(2025·浙江模拟)已知,,且,则( )
A.4 B.2 C. D.1
3.(2025·阳西模拟)若集合,则( )
A. B.
C. D.
4.(2025·阳西模拟)投篮测试中,每人投2次,至少投中1次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
A.0.24 B.0.48 C.0.84 D.0.94
5.(2025·四川模拟)已知圆上恰有两个点到直线的距离为2,则m的取值范围是( )
A. B.
C. D.
6.(2025·揭阳模拟)“物竞天择,适者生存”是大自然环境下选择的结果,森林中某些昆虫会通过向后跳跃的方式来躲避偷袭的天敌.经某生物小组研究表明某类昆虫在水平速度为v(单位:分米/秒)时的跳跃高度H(单位:米)近似满足的等量关系,则该类昆虫的最大跳跃高度约为( )
A.米 B.米 C.米 D.米
7.(2025·雅安模拟)已知正四棱锥的所有顶点都在同一个球面上,若该棱锥的高为1,底面边长为2,则球的体积为( )
A. B. C. D.
8.(2025·威海模拟)已知双曲线的左、右焦点分别为,过的直线与的右支交于两点,若,则的离心率为( )
A. B. C.2 D.
二、多项选择题
9.(2025·浙江模拟)已知,,则下列说法正确的是( )
A.若,则
B.的最小值为1
C.若,则的最小值为8
D.若恒成立,则的最小值为
10.(2025·浙江模拟)已知函数(其中,)的最大值为,其图象的相邻两条对称轴之间的距离为,则下列说法正确的是( )
A.
B.函数的图象向左平移单位后关于原点对称
C.函数的图象关于点对称
D.函数在区间上单调递增
11.(2025·阳西模拟)已知球O是棱长为2的正方体的外接球,为球O的直径,点P为该正方体表面上的一动点,则下列说法中正确的是( )
A.当P为中点时,直线与所成角的余弦值为
B.当三棱锥的体积为时,点P轨迹的长度为2
C.的最小值为
D.的最大值为
三、填空题
12.(2025·浙江模拟)已知的展开式中含项的系数为16,则 .
13.(2025·张掖模拟)已知等比数列的前项积为,若,则 .
14.(2025·北京市模拟)已知直线和曲线,给出下列四个结论:
①存在实数和,使直线和曲线没有交点;
②存在实数,对任意实数,直线和曲线恰有个交点;
③存在实数,对任意实数,直线和曲线不会恰有个交点;
④对任意实数和,直线和曲线不会恰有个交点.
其中所有正确结论的序号是 .
四、解答题
15.(2025·上海市模拟)在中,角,,所对边的边长分别为,,,且满足
(1)求角的值;
(2)若,求周长的最大值.
16.(2025·上海市模拟)如图,为圆锥的顶点,是圆锥底面的圆心,,是底面半径,,为劣弧的中点.
(1)证明:平面;
(2)若圆锥底面半径为1,高为2,求平面与平面所成锐二面角的余弦值.
17.(2025·天河模拟)为减少环境污染,保护生态环境,某校进行了“垃圾分类知识普及活动”,并对高一、高二全体学生进行了相关知识测试.现从高一、高二各随机抽取了20名学生,对他们的成绩(百分制)进行了整理和分析后得到如下信息:
高一年级成绩分布表
成绩
人数 1 2 3 4 10
高二年级成绩频率分布直方图
(1)从高一和高二样本中各抽取一人,求这两人成绩都不低于90分的概率;
(2)用频率估计概率,分别从高一全体学生中抽取一人,从高二全体学生中抽取两人,随机变量表示这三人中成绩不低于90分的人数,求的分布列和数学期望.
18.(2025·浙江模拟)若数列中某相邻三项成等差数列,则称该三项为“等差组”;若数列中某相邻三项成等比数列,则称该三项为“等比组”.现有一个12项的正项数列,其共有10组相邻三项,记第组相邻三项为.
(1)若数列满足,
①为“等差组”,为“等比组”,求;
②为“等比组”,为“等差组”,求.
(2)若数列满足,且为“等差组”或“等比组”,求满足条件的数列的个数;
(3)若数列满足,且中恰有5组“等差组”和5组“等比组”,求的最大可能值.
19.(2025·浙江模拟)已知是椭圆的右焦点,椭圆离心率,且椭圆上任意一点与点距离的最大值为3.
(1)求椭圆的方程;
(2)点在椭圆上,椭圆在点处的切线交轴于点.
①求的最小值;
②设分别为椭圆的左 右顶点,不垂直轴的直线交椭圆于另一点,直线与直线交于点,问直线与直线的交点是否在一条定直线上?若是,求出该直线方程;若不是,请说明理由.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】A,C
10.【答案】A,B,D
11.【答案】A,C,D
12.【答案】2
13.【答案】1
14.【答案】①②③
15.【答案】(1)解:由正弦定理可得,即
由余弦定理可得,
因为所以
(2)解:由余弦定理可知, ,所以
所以
所以,当且仅当时,等号成立,
所以
所以三角形的周长的最大值为
16.【答案】(1)证明:如图所示,连接,
因为点是劣弧的中点,,
所以.
因为,所以为等边三角形.
所以,所以,
因为平面,不在平面上,
所以平面.
(2)解:如图所示,过点作交于点,以,,所在直线分别为轴,轴,轴建立空间直角坐标系
所以、、、,
所以,,,
设平面的一个法向量为,
所以,令,则x1=4,y1=0,
所以,
设平面的一个法向量为,
所以,令,则,,
所以,
所以,
所以平面与平面所成锐二面角的余弦值为.
17.【答案】(1)解:由题意可知:高一年级成绩成绩不低于90分的概率为;
高二年级成绩不低于90分的概率为,
则从高一和高二样本中各抽取1人,这两人的成绩都不低于90分的概率为:;
(2)解:由题意可知,随机变量的可能取值为0,1,2,3,
,
,
,
,
的分布列为:
0 1 2 3
.
18.【答案】(1)①因为为“等差组”,故成等差数列,故,故,而为“等比组”,故成等比数列,故,故.
②若为“等比组”,为“等差组”,则成等比数列,故,
且成等差数列,故.
(2)因为为“等差组”或“等比组”,故有4种情形:若为“等差组”,为“等差组”,则;
若为“等差组”,为“等比组”,则,
而为正项数列,故即,
故,而,故,故,;
若为“等比组”,为“等比组”,则,;
若为“等比组”,为“等差组”,则,
故,而,故,.
从而开始的相邻三项,要么为“等比组”,要么为“等差组”,
对于确定的、,此后等比组的公比、等差组的公差均确定,
故此时有个满足条件的数列,
故满足条件的数列的个数为.
(3)先考虑一个一般命题:若,若正项数列中中一个“等差组”,另一个为“等比组”,则先“等比组”再“等差组”得到的较大.
证明:若先“等差组”,再“等比组”,则,
若先“等比组”,再“等差组”,则,其中,
此时
,
故先“等比组”再“等差组”得到的较大..
再考虑另一个一般命题:若,若正项数列中的为“等差组”或“等比组”,则当增大时,也增大.
证明:若均为“等差组”或“等比组”,
由等差数列的性质和等比数列的性质可得当增大时,也增大.
若先“等差组”,再“等比组”,则,
由得,
故由双勾函数的性质可得增大时,也增大;
若先“等比组”,再“等差组”,则,
而,故增大时,也增大,故命题成立.
对于数列满足,,
而中恰有5组“等差组”和5组“等比组”,
要使得的最大,则前述两个命题可得需前5组为“等比组”,
后5组为“等差组”,此时个数分别为,
故的最大可能值为.
19.【答案】(1)由已知,解得,
所以,所以椭圆方程为;
(2)由已知,解得,
所以,所以椭圆方程为;
(2)
①因为切线交轴于点,所以,,
因为点在椭圆上,所以,即,
又,
因为,所以,所以,
所以,
所以,
当且仅当,即时等号成立,所以的最小值为;
②由已知设直线:,,
由消元得,
则,,
所以,
因为,,所以,
因为,,所以,
所以
,
即点,所以直线的方程为,
与直线联立,得,
因为,所以,代入上式可得
,
即,解得,
即点在直线上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
