【2025秋人教九上数学情境课堂教学课件】 21.2.1.2 配方法 课件(共24张PPT)
文档属性
| 名称 | 【2025秋人教九上数学情境课堂教学课件】 21.2.1.2 配方法 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 20:28:12 | ||
图片预览







文档简介
(共24张PPT)
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.1 配方法
第2课时 配方法
主题情境·柜子刷漆
1.理解并掌握配方法的一般步骤.
2.能根据方程的结构特点熟练、灵活地运用配方法解一元二次方程.
某小区计划设置一块面积为1 200 m2的矩形绿地,并且长比宽多40m. 这块绿地的长、宽各为多少?
解:设矩形绿地的宽为x m,则长为(x + 40)m,
根据长方形面积公式,可得
x ( x + 40 )=1 200
不能直接通过降次解方程
能否将方程转化为可以直接降次的形式再求解呢?
观察 等式左边的常数项和一次项系数有什么关系?对于形如 x2 + ax的式子,如何配成完全平方式?
(1) x2 + 2 x+___= ( )2; (2) x2 + 8 x + ___ = ( x + ____ )2.
1 2
4 2
4
x+1
一半
一半
通过观察可以发现,对于二次项系数为 1 的单字母二次三项式,将常数项配成一次项系数一半的平方时,可得完全平方式.
x2 + ax + ( )2 = ( x + )2
对于形如 x2 + ax的式子,不妨猜测: .
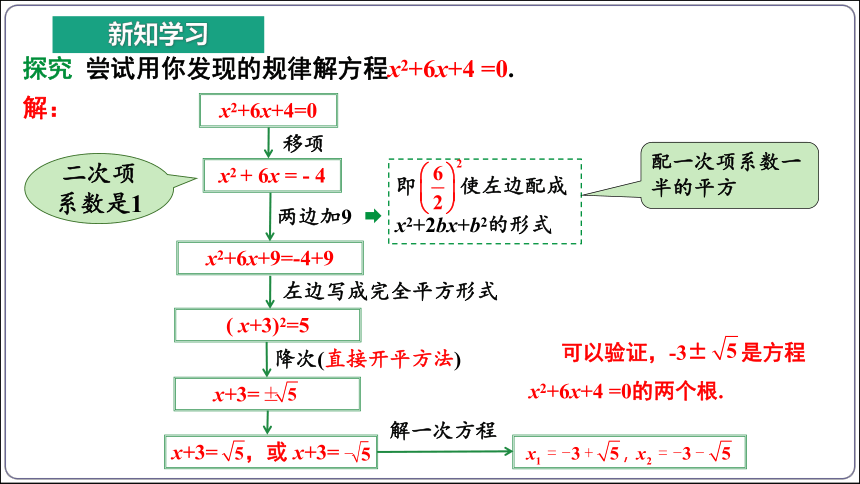
x2 + 6x = - 4
x2+6x+9=-4+9
( x+3)2=5
降次(直接开平方法)
解:
x2+6x+4=0
移项
两边加9
二次项系数是1
即 使左边配成
x2+2bx+b2的形式
左边写成完全平方形式
配一次项系数一半的平方
x+3=
x+3= ,或 x+3=
解一次方程
可以验证,-3± 是方程x2+6x+4 =0的两个根.
探究 尝试用你发现的规律解方程x2+6x+4 =0.
归纳总结
通过配成完全平方形式来解一元二次方程的方法,叫做配方法.
基本思路:将一般式 ax +bx+c=0 (a≠0) 转化为(x+n)2 = p 的形式,再通过直接开平方法(降次),转化为一元一次方程求解.
核心思想:配方是为了降次,把一个一元二次方程转化成两个一元一次方程.
问题解决 某小区计划设置一块面积为1 200 m2的矩形绿地,并且长比宽多40 m. 这块绿底的长、宽各为多少?
解:设矩形绿地的宽为x m,则长为(x + 40)m,
根据长方形面积公式,可得, x ( x + 40 )=1 200 .
化简,得 x2 + 40x = 1 200 .
配方,得 x2 + 40x + (20)2 = 1 200 + (20)2, (x + 20)2 = 1 600 .
由此可得 x + 20 = ±40 ,x1 = 20,x2 = - 60 .
根据问题的实际意义,矩形绿地的宽为20 m,则这块绿地的长为(20+40)=60 m.
(1)x2-8x+1=0
解:移项,得
x2-8x=-1,
由此可得
配方,得
x2-8x+( 4 )2=-1+42,
( x-4)2=15
即
分析:方程的二次项系数为1,直接运用配方法.
例 解下列方程:
(2)2x2+1=3x
分析:先把方程化为2x2 - 3x + 1= 0.它的二次项系数为2,为了便于配方,需将二次项系数化为1,为此方程两边都除以2.
解:移项,得
2x2-3x=-1,
二次项系数化为1,得
配方,得
由此可得
例 解下列方程:
(3)3x2-6x+4=0
例 解下列方程:
分析:与(2)类似,将二次项系数化为1后再配方.
解:移项,得
二次项系数化为1,得
配方,得
因为实数的平方不会是负数,所以 x 取任何实数时,(x-1)2都是非负数,上式都不成立,即原方程无实数根.
变式 应用配方法求最值:
(1) 2x2 - 4x+5的最小值; (2) -3x2 + 6x -7的最大值.
解:原式 = 2(x2 - 2x) +5
= 2(x2 - 2x + 1 ) -2 + 5
= 2(x - 1)2 +3
当x =1时,有最小值3.
解:原式= - 3 (x2 - 2x) - 7
= -3(x2 - 2x + 1 )+3 - 7
= -3(x - 1)2 - 4
当x =1时,有最大值-4.
思考 将一元二次方程通过配方法转化成(x+n)2 = p 形式后,它的根和 p 有什么关系?
一般地,如果一个一元二次方程通过配方转化成
(x+n) =p (Ⅱ)
的形式,那么就有:
(1)当 p > 0时,方程(Ⅱ)有两个不等的实数根:
(2)当 p = 0时,方程(Ⅱ)有两个相等的实数根:
(3)当 p < 0时,因为对任意实数x,都有( x + n )2 ≥ 0 ,所以方程(Ⅱ)无实数根.
配方法解一元二次方程的步骤:
一移,化成一般式,把常数项移到等号右边;
二化,二次项系数化为1(等式两边同时除以二次项系数);
三配,等式两边同时加上一次项系数一半的平方;
四写,方程写成(x+n)2=p的形式;
五开,将等式两边直接开平方;
六解,解一元一次方程;
七定,写出原方程的根.
注意:移项要改变符号
注意:p≥0,才有根.
归纳总结
类别 解题策略
求最值或证明代数式的值恒为正(或负) 对于一个关于x的二次多项式通过配方成 a(x+m)2+n的形式后,(x+m)2≥0,n为常数,当a>0时,可知其最小值;当a<0时,可知其最大值.
利用配方构成非负数和的形式 对于含有多个未知数的二次式的等式,求未知数的值,解题突破口往往是配方成多个完全平方式得其和为 0,再根据非负数的和为 0,各项均为 0,从而求解.
如:a2+b2 - 4b+4=0,则 a2+(b-2)2=0,即 a=0,b=2.
归纳总结
配方法的应用
1. (2023新疆)用配方法解一元二次方程x2-6x+8 = 0配方后得到的方程是( )
A. (x + 6)2 = 28
B. (x - 6)2 = 28
C. (x + 3)2 = 1
D. (x - 3)2 = 1
D
(1) x2 - 4x + 3 = - 1
2. 用配方法解下列方程:
(2)x2 - x + 1 = 25
解:
解:x2 - 4x + 4 = 0
(x - 2)2 = 0
x1 = x2 = 2
(3) 2x2 - 3x - 1 = 1
2. 用配方法解下列方程:
解:
(4) x(x-4) = - 8x + 12
解:x2 + 4x = 12
x2 + 4x + 4 = 16
(x + 2)2 = 16
x1 = 2 ,x2 = - 6
3. 试用配方法说明:不论k取何实数,多项式 k2-2k+4 的值必定大于零.
解:k2-2k+4=k2-2k+1+3
=(k-1)2+3
因为(k-1)2 ≥ 0,所以(k-1)2+3 ≥ 3.
所以k2-2k+4的值必定大于零.
4.(解题方法型阅读理解)【阅读材料】若x +y +8x-6y+25=0,求x,y的值.解:(x2+8x+16)+(y2-6y+9)=0,(x+4)2+(y-3)2=0,
∴x+4=0,y-3=0. ∴x= - 4,y=3.
【解决问题】(1)已知m +n2-12n+10m+61=0,求(m+n)2023的值;
解: (1)∵m +n -12n+10m+61=0,将61拆分为25和36,
可得:(m +10m+25)+(n2-12n+36)=0,
根据完全平方公式得(m+5)2+(n-6)2=0,
∴m+5=0, n-6=0,∴m=-5,n=6,
∴(m+n)2023=(-5+6)2023=1.
(2)已知a,b,c是△ABC的三边长,且b,c满足b2+c2=8b+4c-20, a是△ABC中最长的边,求a的取值范围.
(2) ∵b2 + c2 = 8b + 4c - 20,∴b2 + c2 - 8b - 4c + 20 = 0,
将20拆分为16和4,可得(b2-8b+16)+(c2-4c+4) =0,
根据完全平方公式得(b-4)2+ (c-2)2=0,
∴b - 4 = 0, c - 2 = 0,∴b = 4, c = 2 .
在△ABC中,b - c< a < b + c,即2 < a < 6 .
又∵a是△ABC中最长的边,
∴4 ≤ a<6,即a的取值范围为4 ≤ a <6.
一移,化成一般式,把常数项移到等号右边;
二化,二次项系数化为1(等式两边同时除以二次项系数);
三配,等式两边同时加上一次项系数一半的平方;
四写,方程写成(x+n)2=p的形式;
五开,将等式两边直接开平方;
六解,解一元一次方程;
七定,写出原方程的根.
配方法
通过配成完全平方形式解一元二次方程的方法.
步骤
定义
Thanks!
https://www.21cnjy.com/recruitment/home/fine
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.1 配方法
第2课时 配方法
主题情境·柜子刷漆
1.理解并掌握配方法的一般步骤.
2.能根据方程的结构特点熟练、灵活地运用配方法解一元二次方程.
某小区计划设置一块面积为1 200 m2的矩形绿地,并且长比宽多40m. 这块绿地的长、宽各为多少?
解:设矩形绿地的宽为x m,则长为(x + 40)m,
根据长方形面积公式,可得
x ( x + 40 )=1 200
不能直接通过降次解方程
能否将方程转化为可以直接降次的形式再求解呢?
观察 等式左边的常数项和一次项系数有什么关系?对于形如 x2 + ax的式子,如何配成完全平方式?
(1) x2 + 2 x+___= ( )2; (2) x2 + 8 x + ___ = ( x + ____ )2.
1 2
4 2
4
x+1
一半
一半
通过观察可以发现,对于二次项系数为 1 的单字母二次三项式,将常数项配成一次项系数一半的平方时,可得完全平方式.
x2 + ax + ( )2 = ( x + )2
对于形如 x2 + ax的式子,不妨猜测: .
x2 + 6x = - 4
x2+6x+9=-4+9
( x+3)2=5
降次(直接开平方法)
解:
x2+6x+4=0
移项
两边加9
二次项系数是1
即 使左边配成
x2+2bx+b2的形式
左边写成完全平方形式
配一次项系数一半的平方
x+3=
x+3= ,或 x+3=
解一次方程
可以验证,-3± 是方程x2+6x+4 =0的两个根.
探究 尝试用你发现的规律解方程x2+6x+4 =0.
归纳总结
通过配成完全平方形式来解一元二次方程的方法,叫做配方法.
基本思路:将一般式 ax +bx+c=0 (a≠0) 转化为(x+n)2 = p 的形式,再通过直接开平方法(降次),转化为一元一次方程求解.
核心思想:配方是为了降次,把一个一元二次方程转化成两个一元一次方程.
问题解决 某小区计划设置一块面积为1 200 m2的矩形绿地,并且长比宽多40 m. 这块绿底的长、宽各为多少?
解:设矩形绿地的宽为x m,则长为(x + 40)m,
根据长方形面积公式,可得, x ( x + 40 )=1 200 .
化简,得 x2 + 40x = 1 200 .
配方,得 x2 + 40x + (20)2 = 1 200 + (20)2, (x + 20)2 = 1 600 .
由此可得 x + 20 = ±40 ,x1 = 20,x2 = - 60 .
根据问题的实际意义,矩形绿地的宽为20 m,则这块绿地的长为(20+40)=60 m.
(1)x2-8x+1=0
解:移项,得
x2-8x=-1,
由此可得
配方,得
x2-8x+( 4 )2=-1+42,
( x-4)2=15
即
分析:方程的二次项系数为1,直接运用配方法.
例 解下列方程:
(2)2x2+1=3x
分析:先把方程化为2x2 - 3x + 1= 0.它的二次项系数为2,为了便于配方,需将二次项系数化为1,为此方程两边都除以2.
解:移项,得
2x2-3x=-1,
二次项系数化为1,得
配方,得
由此可得
例 解下列方程:
(3)3x2-6x+4=0
例 解下列方程:
分析:与(2)类似,将二次项系数化为1后再配方.
解:移项,得
二次项系数化为1,得
配方,得
因为实数的平方不会是负数,所以 x 取任何实数时,(x-1)2都是非负数,上式都不成立,即原方程无实数根.
变式 应用配方法求最值:
(1) 2x2 - 4x+5的最小值; (2) -3x2 + 6x -7的最大值.
解:原式 = 2(x2 - 2x) +5
= 2(x2 - 2x + 1 ) -2 + 5
= 2(x - 1)2 +3
当x =1时,有最小值3.
解:原式= - 3 (x2 - 2x) - 7
= -3(x2 - 2x + 1 )+3 - 7
= -3(x - 1)2 - 4
当x =1时,有最大值-4.
思考 将一元二次方程通过配方法转化成(x+n)2 = p 形式后,它的根和 p 有什么关系?
一般地,如果一个一元二次方程通过配方转化成
(x+n) =p (Ⅱ)
的形式,那么就有:
(1)当 p > 0时,方程(Ⅱ)有两个不等的实数根:
(2)当 p = 0时,方程(Ⅱ)有两个相等的实数根:
(3)当 p < 0时,因为对任意实数x,都有( x + n )2 ≥ 0 ,所以方程(Ⅱ)无实数根.
配方法解一元二次方程的步骤:
一移,化成一般式,把常数项移到等号右边;
二化,二次项系数化为1(等式两边同时除以二次项系数);
三配,等式两边同时加上一次项系数一半的平方;
四写,方程写成(x+n)2=p的形式;
五开,将等式两边直接开平方;
六解,解一元一次方程;
七定,写出原方程的根.
注意:移项要改变符号
注意:p≥0,才有根.
归纳总结
类别 解题策略
求最值或证明代数式的值恒为正(或负) 对于一个关于x的二次多项式通过配方成 a(x+m)2+n的形式后,(x+m)2≥0,n为常数,当a>0时,可知其最小值;当a<0时,可知其最大值.
利用配方构成非负数和的形式 对于含有多个未知数的二次式的等式,求未知数的值,解题突破口往往是配方成多个完全平方式得其和为 0,再根据非负数的和为 0,各项均为 0,从而求解.
如:a2+b2 - 4b+4=0,则 a2+(b-2)2=0,即 a=0,b=2.
归纳总结
配方法的应用
1. (2023新疆)用配方法解一元二次方程x2-6x+8 = 0配方后得到的方程是( )
A. (x + 6)2 = 28
B. (x - 6)2 = 28
C. (x + 3)2 = 1
D. (x - 3)2 = 1
D
(1) x2 - 4x + 3 = - 1
2. 用配方法解下列方程:
(2)x2 - x + 1 = 25
解:
解:x2 - 4x + 4 = 0
(x - 2)2 = 0
x1 = x2 = 2
(3) 2x2 - 3x - 1 = 1
2. 用配方法解下列方程:
解:
(4) x(x-4) = - 8x + 12
解:x2 + 4x = 12
x2 + 4x + 4 = 16
(x + 2)2 = 16
x1 = 2 ,x2 = - 6
3. 试用配方法说明:不论k取何实数,多项式 k2-2k+4 的值必定大于零.
解:k2-2k+4=k2-2k+1+3
=(k-1)2+3
因为(k-1)2 ≥ 0,所以(k-1)2+3 ≥ 3.
所以k2-2k+4的值必定大于零.
4.(解题方法型阅读理解)【阅读材料】若x +y +8x-6y+25=0,求x,y的值.解:(x2+8x+16)+(y2-6y+9)=0,(x+4)2+(y-3)2=0,
∴x+4=0,y-3=0. ∴x= - 4,y=3.
【解决问题】(1)已知m +n2-12n+10m+61=0,求(m+n)2023的值;
解: (1)∵m +n -12n+10m+61=0,将61拆分为25和36,
可得:(m +10m+25)+(n2-12n+36)=0,
根据完全平方公式得(m+5)2+(n-6)2=0,
∴m+5=0, n-6=0,∴m=-5,n=6,
∴(m+n)2023=(-5+6)2023=1.
(2)已知a,b,c是△ABC的三边长,且b,c满足b2+c2=8b+4c-20, a是△ABC中最长的边,求a的取值范围.
(2) ∵b2 + c2 = 8b + 4c - 20,∴b2 + c2 - 8b - 4c + 20 = 0,
将20拆分为16和4,可得(b2-8b+16)+(c2-4c+4) =0,
根据完全平方公式得(b-4)2+ (c-2)2=0,
∴b - 4 = 0, c - 2 = 0,∴b = 4, c = 2 .
在△ABC中,b - c< a < b + c,即2 < a < 6 .
又∵a是△ABC中最长的边,
∴4 ≤ a<6,即a的取值范围为4 ≤ a <6.
一移,化成一般式,把常数项移到等号右边;
二化,二次项系数化为1(等式两边同时除以二次项系数);
三配,等式两边同时加上一次项系数一半的平方;
四写,方程写成(x+n)2=p的形式;
五开,将等式两边直接开平方;
六解,解一元一次方程;
七定,写出原方程的根.
配方法
通过配成完全平方形式解一元二次方程的方法.
步骤
定义
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
