【2025秋人教九上数学情境课堂教学课件】 21.2.4 一元二次方程的根与系数的关系 课件(共21张PPT)
文档属性
| 名称 | 【2025秋人教九上数学情境课堂教学课件】 21.2.4 一元二次方程的根与系数的关系 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 20:25:09 | ||
图片预览








文档简介
(共21张PPT)
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.4 一元二次方程根
与系数的关系
1. 了解一元二次方程的根与系数的关系.
2. 会用一元二次方程的根与系数的关系解决简单问题.
方程的两根 x1和 x2与系数a、b、c还有其他关系吗?
1. 方程ax +bx+c=0(a≠0)的求根公式是什么?
2. 如何用判别式 b2 - 4ac 来判断方程 ax2 + bx +c = 0(a≠0)根的情况?
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
从因式分解法可知,方程(x-x1)(x-x2)=0 ( x1,x2为已知数)的两根为x1和x2,将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗
思考1
把方程( x - x1 ) ( x - x2 ) = 0的左边展开,化成一般形式,得
x2 - ( x1 + x2 ) x + x1 x2 = 0
二次项系数为1
一次项系数p = - ( x1+x2 )
常数项q = x1x2
可以发现,方程x2+px+q=0的两根的和、积与系数的关系为:
x1+x2= -p, x1x2=q.
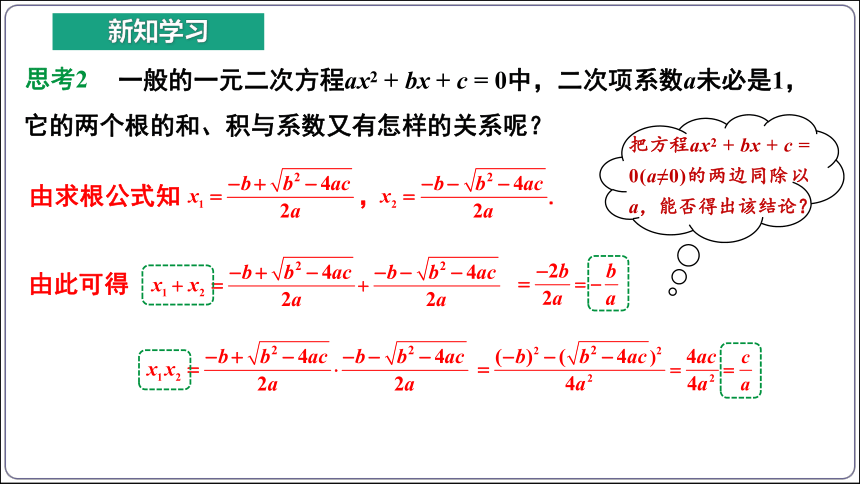
一般的一元二次方程ax2 + bx + c = 0中,二次项系数a未必是1,它的两个根的和、积与系数又有怎样的关系呢?
思考2
由求根公式知 , .
由此可得
把方程ax2 + bx + c = 0(a≠0)的两边同除以a,能否得出该结论?
归纳总结
若 x1,x2是一元二次方程ax2 + bx + c = 0(a≠0)的两个根,则有:
任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数;
两个根的积等于常数项与二次项系数的比.
例1 根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2的和与积:
(1) x2 - 6x - 15 = 0; (2) 3x2 + 7x - 9 = 0; (3) 5x - 1 = 4x2.
解:(1)x1+x2=-(-6)=6,x1x2=-15.
(3)方程化为 4x2-5x+1=0,∴
变式 已知x1,x2 是 一元二次方程 x +ax+16 = 0的两个根, ,求 a 的值.
解:由方程有两个实数根,得 Δ = a2 - 4×1×16 ≥ 0,
即 a ≥ 8或a ≤ -8.
由根与系数的关系得 x1 + x2 = - a,x1 x2 = 16.
所以 ,
解得 a = -16.
运用根与系数的关系需注意前提条件:
(1)方程必须是一元二次方程;
(2)一定要将方程化为一般形式;
(3)方程必须有实数根,即 b2-4 ac ≥0.
例2 已知x1,x2 是 一元二次方程 3x +4x - 3 = 0的两个根,利用根与系数之间的关系,求下列各式的值.
(1) ; (2) ; (3) ; (4) .
解:根据根与系数的关系得:
(1)
(2)
例2 已知x1,x2 是 一元二次方程 3x +4x - 3 = 0的两个根,利用根与系数之间的关系,求下列各式的值.
(1) ; (2) ; (3) ; (4) .
解:根据根与系数的关系得:
(3)
(4)
常见求值公式变形
归纳总结
1.已知关于x的一元二次方程x2+4ax﹣4=0,则此方程根的情况是( )
A. 两个相等的实数根 B.两根之和为﹣4
C. 两根之积为﹣4 D. 无实数根
C
2.(2024绥化)小影与小冬一起写作业,在解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是﹣2和﹣5.则原来的方程是( )
A. x2 + 6x + 5 = 0 B. x2 - 7x + 10 = 0
C. x2 - 5x + 2 = 0 D. x2 - 6x - 10 = 0
B
3.填空:
(1)(2024烟台)若一元二次方程2x2﹣4x﹣1=0的两根为m,n,则3m2﹣4m+n2的值为____________.
6
引导思路
3m2﹣4m+n2
变形
含m+n,mn的形式
2m2﹣4m+(m+n)2﹣2mn
2x2﹣4x﹣1=0
2m2﹣4m = 1
m + n = 2
mn =
代入
求值
m,n为一元二次方程2x2﹣4x﹣1=0的根
(2)(2024成都)若m,n是一元二次方程x2﹣5x+2=0的两个实数根,则m+(n﹣2)2的值为____________.
3.填空:
引导思路
x2﹣5x+2=0
m,n为一元二次方程x2﹣5x + 2=0的根
m2﹣5m= - 2
m+n = 5
n= 5 - m
m+(n﹣2)2可化为
m2﹣5m+ 9
代入
求值
7
4.已知关于x的一元二次方程x2﹣px+1=0 ( p为常数 )有两个不相等的实数根x1和x2.
(1)填空:x1+x2=______,x1x2=_______;
(2)求 , ;
p
1
解:∵x1 + x2 = p,x1x2 = 1,
∴ ;
∵关于x的一元二次方程x2﹣px+1=0 ( p为常数 )有两个不相等的实数根x1和x2 ,
∴x12 - px1 +1 = 0 ,
∴x1- p + = 0 ,即 .
4.已知关于x的一元二次方程x2﹣px+1=0 ( p为常数 )有两个不相等的实数根x1和x2.
(3)已知x12 +x22 = 2p+1,求 p 的值.
解:由根与系数的关系得:x1 + x2 = p,x1x2 = 1,
∵x12 +x22 = 2p+1,
∴(x1 +x2)2 ﹣2x1x2= 2p+1,∴p2﹣2 = 2p + 1,
解得 p1 = 3,p2 = ﹣1,
当 p=3 时,Δ=p2﹣4=9﹣4=5>0;
当 p=﹣1 时,Δ=p2﹣4=﹣3<0; ∴p=3.
若 x1,x2是一元二次方程 ax2 + bx + c = 0 (a≠0) 的两个根,则有:
常见应用
一元二次方程的
根与系数的关系
内容
Thanks!
https://www.21cnjy.com/recruitment/home/fine
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.4 一元二次方程根
与系数的关系
1. 了解一元二次方程的根与系数的关系.
2. 会用一元二次方程的根与系数的关系解决简单问题.
方程的两根 x1和 x2与系数a、b、c还有其他关系吗?
1. 方程ax +bx+c=0(a≠0)的求根公式是什么?
2. 如何用判别式 b2 - 4ac 来判断方程 ax2 + bx +c = 0(a≠0)根的情况?
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
从因式分解法可知,方程(x-x1)(x-x2)=0 ( x1,x2为已知数)的两根为x1和x2,将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗
思考1
把方程( x - x1 ) ( x - x2 ) = 0的左边展开,化成一般形式,得
x2 - ( x1 + x2 ) x + x1 x2 = 0
二次项系数为1
一次项系数p = - ( x1+x2 )
常数项q = x1x2
可以发现,方程x2+px+q=0的两根的和、积与系数的关系为:
x1+x2= -p, x1x2=q.
一般的一元二次方程ax2 + bx + c = 0中,二次项系数a未必是1,它的两个根的和、积与系数又有怎样的关系呢?
思考2
由求根公式知 , .
由此可得
把方程ax2 + bx + c = 0(a≠0)的两边同除以a,能否得出该结论?
归纳总结
若 x1,x2是一元二次方程ax2 + bx + c = 0(a≠0)的两个根,则有:
任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数;
两个根的积等于常数项与二次项系数的比.
例1 根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2的和与积:
(1) x2 - 6x - 15 = 0; (2) 3x2 + 7x - 9 = 0; (3) 5x - 1 = 4x2.
解:(1)x1+x2=-(-6)=6,x1x2=-15.
(3)方程化为 4x2-5x+1=0,∴
变式 已知x1,x2 是 一元二次方程 x +ax+16 = 0的两个根, ,求 a 的值.
解:由方程有两个实数根,得 Δ = a2 - 4×1×16 ≥ 0,
即 a ≥ 8或a ≤ -8.
由根与系数的关系得 x1 + x2 = - a,x1 x2 = 16.
所以 ,
解得 a = -16.
运用根与系数的关系需注意前提条件:
(1)方程必须是一元二次方程;
(2)一定要将方程化为一般形式;
(3)方程必须有实数根,即 b2-4 ac ≥0.
例2 已知x1,x2 是 一元二次方程 3x +4x - 3 = 0的两个根,利用根与系数之间的关系,求下列各式的值.
(1) ; (2) ; (3) ; (4) .
解:根据根与系数的关系得:
(1)
(2)
例2 已知x1,x2 是 一元二次方程 3x +4x - 3 = 0的两个根,利用根与系数之间的关系,求下列各式的值.
(1) ; (2) ; (3) ; (4) .
解:根据根与系数的关系得:
(3)
(4)
常见求值公式变形
归纳总结
1.已知关于x的一元二次方程x2+4ax﹣4=0,则此方程根的情况是( )
A. 两个相等的实数根 B.两根之和为﹣4
C. 两根之积为﹣4 D. 无实数根
C
2.(2024绥化)小影与小冬一起写作业,在解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是﹣2和﹣5.则原来的方程是( )
A. x2 + 6x + 5 = 0 B. x2 - 7x + 10 = 0
C. x2 - 5x + 2 = 0 D. x2 - 6x - 10 = 0
B
3.填空:
(1)(2024烟台)若一元二次方程2x2﹣4x﹣1=0的两根为m,n,则3m2﹣4m+n2的值为____________.
6
引导思路
3m2﹣4m+n2
变形
含m+n,mn的形式
2m2﹣4m+(m+n)2﹣2mn
2x2﹣4x﹣1=0
2m2﹣4m = 1
m + n = 2
mn =
代入
求值
m,n为一元二次方程2x2﹣4x﹣1=0的根
(2)(2024成都)若m,n是一元二次方程x2﹣5x+2=0的两个实数根,则m+(n﹣2)2的值为____________.
3.填空:
引导思路
x2﹣5x+2=0
m,n为一元二次方程x2﹣5x + 2=0的根
m2﹣5m= - 2
m+n = 5
n= 5 - m
m+(n﹣2)2可化为
m2﹣5m+ 9
代入
求值
7
4.已知关于x的一元二次方程x2﹣px+1=0 ( p为常数 )有两个不相等的实数根x1和x2.
(1)填空:x1+x2=______,x1x2=_______;
(2)求 , ;
p
1
解:∵x1 + x2 = p,x1x2 = 1,
∴ ;
∵关于x的一元二次方程x2﹣px+1=0 ( p为常数 )有两个不相等的实数根x1和x2 ,
∴x12 - px1 +1 = 0 ,
∴x1- p + = 0 ,即 .
4.已知关于x的一元二次方程x2﹣px+1=0 ( p为常数 )有两个不相等的实数根x1和x2.
(3)已知x12 +x22 = 2p+1,求 p 的值.
解:由根与系数的关系得:x1 + x2 = p,x1x2 = 1,
∵x12 +x22 = 2p+1,
∴(x1 +x2)2 ﹣2x1x2= 2p+1,∴p2﹣2 = 2p + 1,
解得 p1 = 3,p2 = ﹣1,
当 p=3 时,Δ=p2﹣4=9﹣4=5>0;
当 p=﹣1 时,Δ=p2﹣4=﹣3<0; ∴p=3.
若 x1,x2是一元二次方程 ax2 + bx + c = 0 (a≠0) 的两个根,则有:
常见应用
一元二次方程的
根与系数的关系
内容
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
