【2025秋人教九上数学情境课堂教学课件】 21.3.1 传播问题、循环问题和数字问题 课件(共28张PPT)
文档属性
| 名称 | 【2025秋人教九上数学情境课堂教学课件】 21.3.1 传播问题、循环问题和数字问题 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 29.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 20:38:16 | ||
图片预览







文档简介
(共28张PPT)
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.3 实际问题与一元二次方程
第1课时 传播问题、
循环问题和数字问题
1.能正确分析实际问题中的数量关系.
2.能根据实际问题中的等量关系,列出一元二次方程解决相关实际问题.
3.感受用一元二次方程解决相关实际问题的必要性以及在实际背景下检验解的合理性,增强应用意识.
点击播放视频
观看右边视频,了解传染病的特征和防护措施.
传染病是如何传播的呢?
让我们通过一道流感传播问题来看看吧.
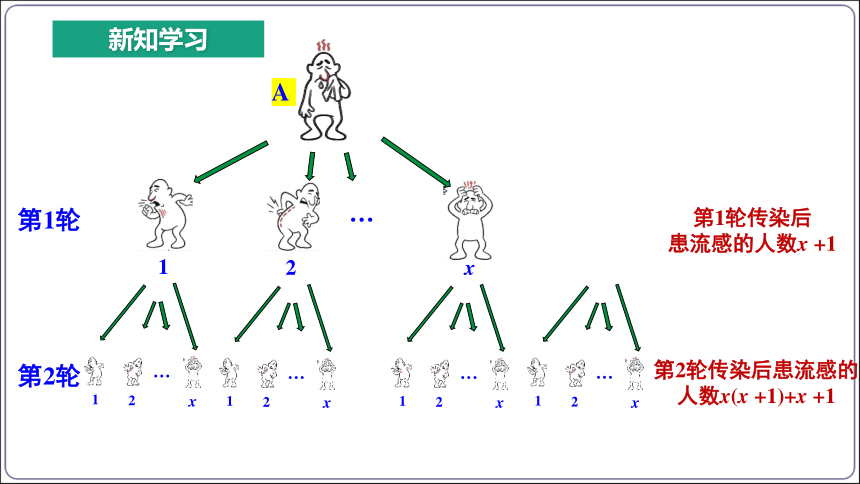
有一个人患了流感,经过两轮传染后共有 121 个人患了流感,每轮传染中平均一个人传染了几个人?
分析:设每轮传染中平均一个人传染了 x 个人.
探究 1
第1轮
第1轮传染后
患流感的人数x +1
···
1
2
x
A
第2轮
···
1
2
x
···
1
2
x
···
1
2
x
A
···
1
2
x
第2轮传染后患流感的人数x(x +1)+x +1
有一个人患了流感,经过两轮传染后共有 121 个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了 x 个人.
列方程 x+1+x(x+1)=121
解方程,得 x1=10,x2= -12(不合题意,舍去)
答:平均一个人传染了 10个人.
探究 1
传播问题
方法总结
问题 类比解决一次方程 ( 组 ) 实际问题的一般步骤写出解决一元二次方程实际问题的一般步骤.
实际问题
建立一元二
次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系设未知数
检 验
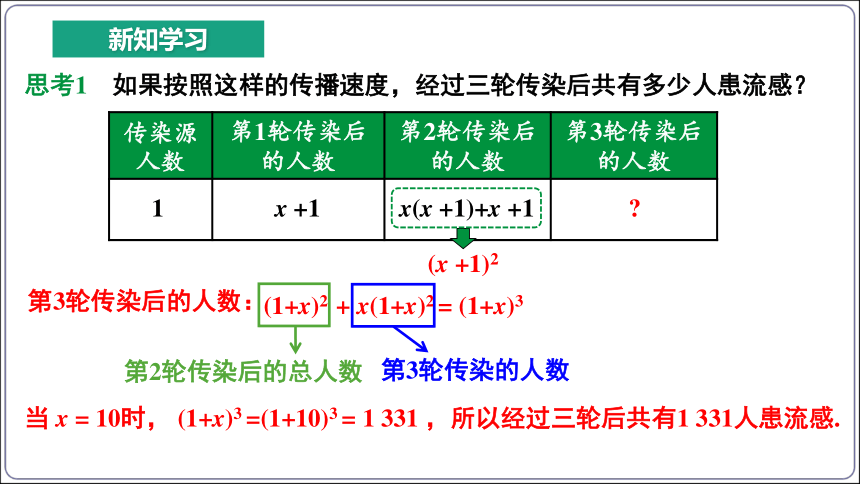
思考1 如果按照这样的传播速度,经过三轮传染后共有多少人患流感?
传染源人数 第1轮传染后的人数 第2轮传染后的人数 第3轮传染后的人数
1
x +1
x(x +1)+x +1
第3轮传染后的人数:
(1+x)2 + x(1+x)2 = (1+x)3
第2轮传染后的总人数
第3轮传染的人数
(x +1)2
当 x = 10时, (1+x)3 =(1+10)3 = 1 331 ,所以经过三轮后共有1 331人患流感.
思考2 观察上面的式子你发现了什么?并回答n轮传染后有多少人患流感
发现了是第几轮传染后的人数就是(1+x)的几次方,
所以第n轮传染后有(1+x)n 个人患流感.
传染源人数 第1轮传染后的人数 第2轮传染后的人数 第3轮传染后的人数
1
x +1
(x +1)2
(x +1)3
变式 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少个小分支?
只有1个主干
1个主干产生 x个支干
1个支干产生x个小分支,所以x个支干会产生(x· x)个小分支
解:设每个支干长出x个小分支.
列方程 1 + x + x · x=91.
解方程,得x1 = 9,x2 = -10 (不合题意,舍去).
答:每个支干长出9个小分支.
方法总结
(1)传播问题中最开始的感染者在第一轮传播给n个人,第二轮会继续传播,所以第二轮有n(n+1)人被传播,总共有1+n+n(n+1)个人被传播.
(2)树干问题中主干长出n个支干,第二轮主干不再分支,n个支干进行分支,第二轮有n2 个支干,主干和支干总共有1+n+n2 个.
循环问题
学校组织了一次篮球单循环比赛(每两队之间都进行了一次比赛),共进行了15场比赛,那么有几个球队参加了这次比赛?
第1队
···
其他(n-1)个参赛队
第2队
第3队
第n队
分析:每个队要和其他(n - 1)个队比赛一场.
两个队之间只需要比赛一场,
所以n个队共有 场比赛.
探究 2
解:设有n个球队参加了这次比赛.
由题意,得 =15.
解得n1=6,n2= - 5(不合题意,舍去)
答:有6个球队参加了这次比赛.
学校组织了一次篮球单循环比赛(每两队之间都进行了一次比赛),共进行了15场比赛,那么有几个球队参加了这次比赛?
循环问题
探究 2
变式 某校九年级组织一次篮球赛,各班均组队参赛,每两班之间都进行两场比赛,共需比赛12场,则九年级班级的个数为多少?
分析:每个队要和其他 (n-1) 个队比赛一场,两个队之间需要比赛2场,所以 n 个队共有 n(n-1) 场比赛.
解:设九年级班级的个数为n,则:n(n-1)=12
解得n1=4,n2= - 3 (不合题意,舍去)
答:九年级班级的个数为4个
方法总结
循环问题包括单循环问题和双循环问题,以比赛背景为例:
设比赛场数为N,队伍数量为n,则:
单循环比赛:N= .
双循环比赛:N= n (n-1) .
数字问题
有一个两位数等于其各位数字之积的3倍,其十位数字比个位数字小2,求这个两位数.
解:设这个两位数的个位数字为x,则十位数字为 (x-2),这个两位数字是 10 (x-2) + x.
根据题意,得10 (x-2) +x=3x (x-2),
整理,得3x2-17x + 20=0,
解得, x1=4,x2= (不合题意,舍去),
当 x=4时,x-2=2,∴这个两位数是24.
探究 3
方法总结
整数的常用表示方法:
①两位数=十位上的数字×10 + 个位上的数字;
②三位数=百位上的数字×100 + 十位上的数字×10 + 个位上的数字;
③三个连续的整数,令最小的数为x,则中间的数为x+1,最大的数为x+2.
1.为了宣传环保,某学生写了一份倡议书在微博传播,规则为:将倡议书发表在自己的微博,再邀请 n 个好友转发倡议书,每个好友转发倡议书,又邀请 n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有1641人参与了传播活动,则方程可列为( )
A.(n+1)2=1641 B.(n﹣1)2=1641
C.n(n+1)=1641 D.1+n+n2=1641
D
2.(2024河北)淇淇在计算正数a的平方时,误算成a与2的积,求得的答案比正确答案小1,则a = ( )
C
A.1 B.
C. D.
3.中秋节到了,班上某个小组的每位同学都互赠了礼物,共送出了30份礼物,这个小组的人数为( )
C
A.4人 B.5人
C.6人 D.7人
4.某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有 81 台电脑被感染. 请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过 700 台?
解:设每轮感染中平均一台电脑会感染 x 台电脑.
则(1 + x)2 = 81,解得x1 = 8, x2 = 10(不合题意,舍去).
(1 + 8)3 = 729(台).
答:每轮感染中平均一台电脑会感染 8 台电脑,若病毒得不到有效控制,三轮感染后,被感染的电脑会超过 700 台,达到 729 台.
5.(代数推理)在学习一元二次方程的课堂上,老师设计了“猜数字”游戏.
规则:由一名同学写出一个两位数,然后告诉大家这个两位数个位与十位上的数字之和,再将之位置交换,告诉大家交换后的新两位数与开始的两位数的乘积,最后大家根据已知信息猜一猜原来的两位数是多少.
下面是小红同学给出的信息,请“猜一猜”小红所写的两位数是多少?
信息1:个位与十位上的数字之和为3;
信息2:个位与十位上的数字交换位置后组成的新两位数与开始写的两位数的乘积为252;
信息3:原数个位上的数字小于十位上的数字.
解:设小红所写的两位数十位上的数字为 x,则个位上的数字为( 3 - x ),
交换位置前的两位数为 10x+(3-x) = 9x + 3,
交换位置后的两位数为 10(3-x)+x = 30 - 9x,
由题意可知,(9x+3)(30-9x)=252,
解得x1=2,x2=1(不合题意,舍去)
∵3-x=1,
∴这个两位数是21.
信息1:个位与十位上的数字之和为3;
信息2:个位与十位上的数字交换位置后组成的新两位数与开始写的两位数的乘积为252;
信息3:原数个位上的数字小于十位上的数字.
(1)传播问题中最开始的感染者在第一轮传播给n个人,第二轮会继续传播,所以第二轮有n(n+1)人被传播,总共有1+n+n(n+1)个人被传播.
(2)树干问题中主干长出n个支干,第二轮主干不再分支,n个支干进行分支,第二轮有n2个支干,主干和支干总共有1+n+n2个.
传播问题
传播问题、
循环问题和
数字问题
解一元二次方程
应用题的步骤
循环比赛问题包括单循环问题和双循环问题,以比赛背景为例:
设比赛场数为N,队伍数量为n,
单循环比赛:N= .
双循环比赛:N= n (n-1) .
整数的常用表示方法:
①两位数=十位上的数字×10 +个位上的数字;
②三位数=百位上的数字×100 +十位上的数字×10 +个位上的数字;
③三个连续的整数,令最小的数为x,则中间的数为x+1,最大的数为x+2.
循环问题
数字问题
传播问题、
循环问题和
数字问题
Thanks!
https://www.21cnjy.com/recruitment/home/fine
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.3 实际问题与一元二次方程
第1课时 传播问题、
循环问题和数字问题
1.能正确分析实际问题中的数量关系.
2.能根据实际问题中的等量关系,列出一元二次方程解决相关实际问题.
3.感受用一元二次方程解决相关实际问题的必要性以及在实际背景下检验解的合理性,增强应用意识.
点击播放视频
观看右边视频,了解传染病的特征和防护措施.
传染病是如何传播的呢?
让我们通过一道流感传播问题来看看吧.
有一个人患了流感,经过两轮传染后共有 121 个人患了流感,每轮传染中平均一个人传染了几个人?
分析:设每轮传染中平均一个人传染了 x 个人.
探究 1
第1轮
第1轮传染后
患流感的人数x +1
···
1
2
x
A
第2轮
···
1
2
x
···
1
2
x
···
1
2
x
A
···
1
2
x
第2轮传染后患流感的人数x(x +1)+x +1
有一个人患了流感,经过两轮传染后共有 121 个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了 x 个人.
列方程 x+1+x(x+1)=121
解方程,得 x1=10,x2= -12(不合题意,舍去)
答:平均一个人传染了 10个人.
探究 1
传播问题
方法总结
问题 类比解决一次方程 ( 组 ) 实际问题的一般步骤写出解决一元二次方程实际问题的一般步骤.
实际问题
建立一元二
次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系设未知数
检 验
思考1 如果按照这样的传播速度,经过三轮传染后共有多少人患流感?
传染源人数 第1轮传染后的人数 第2轮传染后的人数 第3轮传染后的人数
1
x +1
x(x +1)+x +1
第3轮传染后的人数:
(1+x)2 + x(1+x)2 = (1+x)3
第2轮传染后的总人数
第3轮传染的人数
(x +1)2
当 x = 10时, (1+x)3 =(1+10)3 = 1 331 ,所以经过三轮后共有1 331人患流感.
思考2 观察上面的式子你发现了什么?并回答n轮传染后有多少人患流感
发现了是第几轮传染后的人数就是(1+x)的几次方,
所以第n轮传染后有(1+x)n 个人患流感.
传染源人数 第1轮传染后的人数 第2轮传染后的人数 第3轮传染后的人数
1
x +1
(x +1)2
(x +1)3
变式 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少个小分支?
只有1个主干
1个主干产生 x个支干
1个支干产生x个小分支,所以x个支干会产生(x· x)个小分支
解:设每个支干长出x个小分支.
列方程 1 + x + x · x=91.
解方程,得x1 = 9,x2 = -10 (不合题意,舍去).
答:每个支干长出9个小分支.
方法总结
(1)传播问题中最开始的感染者在第一轮传播给n个人,第二轮会继续传播,所以第二轮有n(n+1)人被传播,总共有1+n+n(n+1)个人被传播.
(2)树干问题中主干长出n个支干,第二轮主干不再分支,n个支干进行分支,第二轮有n2 个支干,主干和支干总共有1+n+n2 个.
循环问题
学校组织了一次篮球单循环比赛(每两队之间都进行了一次比赛),共进行了15场比赛,那么有几个球队参加了这次比赛?
第1队
···
其他(n-1)个参赛队
第2队
第3队
第n队
分析:每个队要和其他(n - 1)个队比赛一场.
两个队之间只需要比赛一场,
所以n个队共有 场比赛.
探究 2
解:设有n个球队参加了这次比赛.
由题意,得 =15.
解得n1=6,n2= - 5(不合题意,舍去)
答:有6个球队参加了这次比赛.
学校组织了一次篮球单循环比赛(每两队之间都进行了一次比赛),共进行了15场比赛,那么有几个球队参加了这次比赛?
循环问题
探究 2
变式 某校九年级组织一次篮球赛,各班均组队参赛,每两班之间都进行两场比赛,共需比赛12场,则九年级班级的个数为多少?
分析:每个队要和其他 (n-1) 个队比赛一场,两个队之间需要比赛2场,所以 n 个队共有 n(n-1) 场比赛.
解:设九年级班级的个数为n,则:n(n-1)=12
解得n1=4,n2= - 3 (不合题意,舍去)
答:九年级班级的个数为4个
方法总结
循环问题包括单循环问题和双循环问题,以比赛背景为例:
设比赛场数为N,队伍数量为n,则:
单循环比赛:N= .
双循环比赛:N= n (n-1) .
数字问题
有一个两位数等于其各位数字之积的3倍,其十位数字比个位数字小2,求这个两位数.
解:设这个两位数的个位数字为x,则十位数字为 (x-2),这个两位数字是 10 (x-2) + x.
根据题意,得10 (x-2) +x=3x (x-2),
整理,得3x2-17x + 20=0,
解得, x1=4,x2= (不合题意,舍去),
当 x=4时,x-2=2,∴这个两位数是24.
探究 3
方法总结
整数的常用表示方法:
①两位数=十位上的数字×10 + 个位上的数字;
②三位数=百位上的数字×100 + 十位上的数字×10 + 个位上的数字;
③三个连续的整数,令最小的数为x,则中间的数为x+1,最大的数为x+2.
1.为了宣传环保,某学生写了一份倡议书在微博传播,规则为:将倡议书发表在自己的微博,再邀请 n 个好友转发倡议书,每个好友转发倡议书,又邀请 n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有1641人参与了传播活动,则方程可列为( )
A.(n+1)2=1641 B.(n﹣1)2=1641
C.n(n+1)=1641 D.1+n+n2=1641
D
2.(2024河北)淇淇在计算正数a的平方时,误算成a与2的积,求得的答案比正确答案小1,则a = ( )
C
A.1 B.
C. D.
3.中秋节到了,班上某个小组的每位同学都互赠了礼物,共送出了30份礼物,这个小组的人数为( )
C
A.4人 B.5人
C.6人 D.7人
4.某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有 81 台电脑被感染. 请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,三轮感染后,被感染的电脑会不会超过 700 台?
解:设每轮感染中平均一台电脑会感染 x 台电脑.
则(1 + x)2 = 81,解得x1 = 8, x2 = 10(不合题意,舍去).
(1 + 8)3 = 729(台).
答:每轮感染中平均一台电脑会感染 8 台电脑,若病毒得不到有效控制,三轮感染后,被感染的电脑会超过 700 台,达到 729 台.
5.(代数推理)在学习一元二次方程的课堂上,老师设计了“猜数字”游戏.
规则:由一名同学写出一个两位数,然后告诉大家这个两位数个位与十位上的数字之和,再将之位置交换,告诉大家交换后的新两位数与开始的两位数的乘积,最后大家根据已知信息猜一猜原来的两位数是多少.
下面是小红同学给出的信息,请“猜一猜”小红所写的两位数是多少?
信息1:个位与十位上的数字之和为3;
信息2:个位与十位上的数字交换位置后组成的新两位数与开始写的两位数的乘积为252;
信息3:原数个位上的数字小于十位上的数字.
解:设小红所写的两位数十位上的数字为 x,则个位上的数字为( 3 - x ),
交换位置前的两位数为 10x+(3-x) = 9x + 3,
交换位置后的两位数为 10(3-x)+x = 30 - 9x,
由题意可知,(9x+3)(30-9x)=252,
解得x1=2,x2=1(不合题意,舍去)
∵3-x=1,
∴这个两位数是21.
信息1:个位与十位上的数字之和为3;
信息2:个位与十位上的数字交换位置后组成的新两位数与开始写的两位数的乘积为252;
信息3:原数个位上的数字小于十位上的数字.
(1)传播问题中最开始的感染者在第一轮传播给n个人,第二轮会继续传播,所以第二轮有n(n+1)人被传播,总共有1+n+n(n+1)个人被传播.
(2)树干问题中主干长出n个支干,第二轮主干不再分支,n个支干进行分支,第二轮有n2个支干,主干和支干总共有1+n+n2个.
传播问题
传播问题、
循环问题和
数字问题
解一元二次方程
应用题的步骤
循环比赛问题包括单循环问题和双循环问题,以比赛背景为例:
设比赛场数为N,队伍数量为n,
单循环比赛:N= .
双循环比赛:N= n (n-1) .
整数的常用表示方法:
①两位数=十位上的数字×10 +个位上的数字;
②三位数=百位上的数字×100 +十位上的数字×10 +个位上的数字;
③三个连续的整数,令最小的数为x,则中间的数为x+1,最大的数为x+2.
循环问题
数字问题
传播问题、
循环问题和
数字问题
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
