【2025秋人教九上数学情境课堂教学课件】21.2.1.1 直接开平方法(主题情境:柜子刷漆) 课件(共21张PPT)
文档属性
| 名称 | 【2025秋人教九上数学情境课堂教学课件】21.2.1.1 直接开平方法(主题情境:柜子刷漆) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 20:36:00 | ||
图片预览







文档简介
(共21张PPT)
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.1 配方法
第1课时 直接开平方法
主题情境·柜子刷漆
1. 理解一元二次方程降次的转化思想,会运用开平方法解形如
x2 = p 或 (x+n)2 = p (p≥0) 的方程.
2. 熟练运用直接开平方法解一元二次方程.
李林家要翻新家里正方体形状的柜子,为了避免浪费,需要估算出所需油漆的量.
这是一道很有趣的数学问题,棱长和所用油漆量之间有什么关系呢?
解:设其中一个柜子的棱长为x dm,
则这个柜子的表面积为 6x2 dm2.
根据一桶油漆可刷的面积,列出方程
10×6x2 = 1500. ①
从工人师傅那获悉,一个小桶油漆可刷的面积为 1 500 dm2,恰好能刷完李林家10个同样的正方体形状柜子的全部外表面,李林很快的算出自己家柜子的棱长?你知道他是怎么算的吗?
x dm
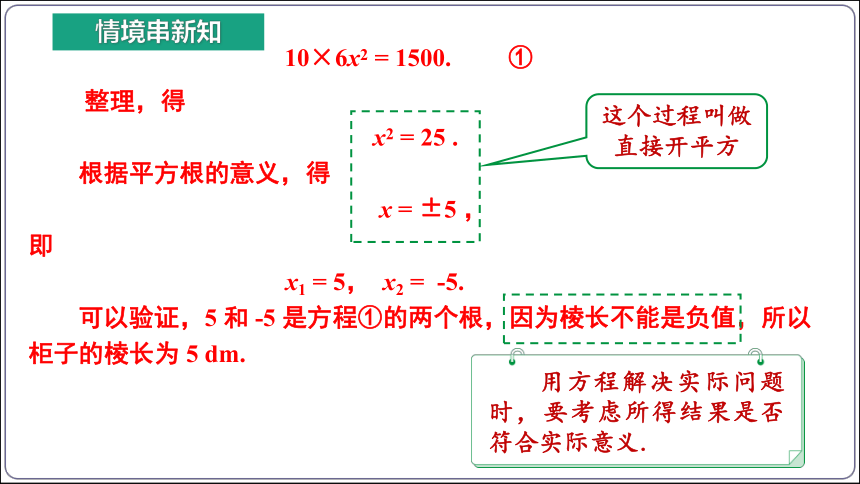
整理,得
x2 = 25 .
根据平方根的意义,得
x = ±5 ,
即
x1 = 5, x2 = -5.
可以验证,5 和 -5 是方程①的两个根,因为棱长不能是负值,所以柜子的棱长为 5 dm.
这个过程叫做直接开平方
用方程解决实际问题时,要考虑所得结果是否符合实际意义.
10×6x2 = 1500. ①
归纳总结
利用平方根的意义直接开平方来求一元二次方程的解的方法叫做直接开平方法.
试一试 解下列方程,并说明你所用的方法.
(1) x2=4
(2) x2=0
(3) x2+1=0
解:根据平方根的意义,得
x1=2, x2=-2.
解:根据平方根的意义,得
x1=x2=0.
解:整理,得x2 = - 1,
因为负数没有平方根,所以原方程无解.
思考 若 x2=p ,则x的值是多少呢?
方程左边x2≥0,右边p的取值不确定,可能是正数、0或负数,因此要分类讨论.
(2)当 p=0 时,方程有两个相等的实数根 x1 = x2 = 0;
(3)当 p<0 时,因为对任意实数 x,都有 x2≥0,所以方程无实数根.
一般地,对于方程 x2 = p ,
(1)当 p>0 时,根据平方根的意义,方程有两个不等的实数根
, ;
聪明的李林又发现,一个大桶油漆可刷的面积为 2 400 dm2,这桶油漆恰好能刷完比妈妈房间柜子的棱长长 2 dm的8个正方体柜子的全部外表面,你能算出妈妈房间柜子的棱长吗?
解:设妈妈房间柜子的棱长为x dm,
则大桶油漆要刷的每个正方体柜子的表面积为 6(x+2)2 dm2,
根据一桶油漆可刷的面积,列出方程 8×6 (x+2)2 = 2400.
整理,得 (x+2)2= 50 .
这个方程可以直接开平方吗?
对照 x2 = 25的解法,试一试怎样解方程 (x+2)2= 50
将x+2看成一个整体
解: (x+2)2=50
直接开平方得
即
解得
一元二次方程
一元一次方程
降次
从以上的解法中,你发现了什么?
思考
一元二次方程
(代数式)2=常数
一元一次方程
转化
开平方
降次
解一元二次方程的思路是将方程转化为 ( x + m )2 = p的形式,它的一边是一个完全平方式,另一边是一个常数,当 p ≥ 0 时,两边同时开平方,转化为一元一次方程,便可求出它的根.
方法总结
用直接开平方法解一元二次方程的步骤:
(1)将方程化为x2=p或(mx+n)2=p ( p ≥ 0,m≠0)的形式;
(2)直接开平方化为两个一元一次方程;
(3)解两个一元一次方程得到原方程的解.
(1) 2x2 - 900=x2;
解:(1)移项,得
x2 = 900.
直接开平方,得
x = ±30,
即x1=30,x2=-30.
例 用直接开平方法解下列方程:
(2) x - 6x + 9 =16.
解:(2) x - 6x+9 = (x - 3) = 16
直接开平方,得
x - 3 = ±4 ,
即x1= 7
,x2= -1 .
1. 如图,这是一个简单的数值运算程序,则输入 x 的值为( )
A.x1=2,x2=﹣2 B.x1=3,x2=﹣3
C.x1=3,x2=﹣1 D.x1=﹣3,x2=1
C
2.对于一元二次方程x2=m-1.
(1)若方程有两个不相等的实数根,则m________;
(2)若方程有两个相等的实数根,则m________;
(3)若方程无实数根,则m________.
m-1>0
>1
m-1= 0
=1
m-1< 0
<1
(1) (x+1)2 - 3 = 2 ;
3. 计算:
(2) 2x2-8=-10;
解:
(2)移项,得2x2 = - 2,
系数化为1,得x2 = - 1,
因为-1无法开平方,所以方程无解.
解:(1) 移项,得 (x + 1) =5,
直接开平方得:
即x1=
,x2= .
x+1= ,
(3)(2x-1)2=(x-2)2 ;
3. 计算:
解:(3)直接开平方得:
2x-1= ,
即 2x-1=±(x-2) ,
∴2x-1=x-2或 2x-1 = - x+2 ,
即x1=-1,x2=1.
(4) x2 - x + 6 = 0 .
解:(4)x2 - x + 6
= ( x - )2 = 0.
直接开平方得:x - = 0
即x1 = x2= .
4. (新定义运算)在实数范围内定义运算“ ”,其法则为:a b = a2 - b2,求方程(4 3) x = 24的解.
解:∵a b = a2 - b2,
∴(4 3) x = (42 - 32) x = 7 x = 72 - x2,
∴ 72 - x2 = 24,
∴ x2 = 25,
∴ x = ±5.
利用平方根的意义直接开平方来求一元二次方程的解的方法叫做直接开平方法.
直接开
平方法
方程x2=p的
根的情况
概念
(1)将方程化为x2=p或(mx+n)2=p(p≥0,m≠0)的形式;
(2)直接开平方化为两个一元一次方程;
(3)解两个一元一次方程得到原方程的解.
步骤
Thanks!
https://www.21cnjy.com/recruitment/home/fine
人教新版 九上 数学
同步课件
2025年秋人教九上数学情境课堂教学课件
第二十一章 一元二次方程
21.2 解一元二次方程
21.2.1 配方法
第1课时 直接开平方法
主题情境·柜子刷漆
1. 理解一元二次方程降次的转化思想,会运用开平方法解形如
x2 = p 或 (x+n)2 = p (p≥0) 的方程.
2. 熟练运用直接开平方法解一元二次方程.
李林家要翻新家里正方体形状的柜子,为了避免浪费,需要估算出所需油漆的量.
这是一道很有趣的数学问题,棱长和所用油漆量之间有什么关系呢?
解:设其中一个柜子的棱长为x dm,
则这个柜子的表面积为 6x2 dm2.
根据一桶油漆可刷的面积,列出方程
10×6x2 = 1500. ①
从工人师傅那获悉,一个小桶油漆可刷的面积为 1 500 dm2,恰好能刷完李林家10个同样的正方体形状柜子的全部外表面,李林很快的算出自己家柜子的棱长?你知道他是怎么算的吗?
x dm
整理,得
x2 = 25 .
根据平方根的意义,得
x = ±5 ,
即
x1 = 5, x2 = -5.
可以验证,5 和 -5 是方程①的两个根,因为棱长不能是负值,所以柜子的棱长为 5 dm.
这个过程叫做直接开平方
用方程解决实际问题时,要考虑所得结果是否符合实际意义.
10×6x2 = 1500. ①
归纳总结
利用平方根的意义直接开平方来求一元二次方程的解的方法叫做直接开平方法.
试一试 解下列方程,并说明你所用的方法.
(1) x2=4
(2) x2=0
(3) x2+1=0
解:根据平方根的意义,得
x1=2, x2=-2.
解:根据平方根的意义,得
x1=x2=0.
解:整理,得x2 = - 1,
因为负数没有平方根,所以原方程无解.
思考 若 x2=p ,则x的值是多少呢?
方程左边x2≥0,右边p的取值不确定,可能是正数、0或负数,因此要分类讨论.
(2)当 p=0 时,方程有两个相等的实数根 x1 = x2 = 0;
(3)当 p<0 时,因为对任意实数 x,都有 x2≥0,所以方程无实数根.
一般地,对于方程 x2 = p ,
(1)当 p>0 时,根据平方根的意义,方程有两个不等的实数根
, ;
聪明的李林又发现,一个大桶油漆可刷的面积为 2 400 dm2,这桶油漆恰好能刷完比妈妈房间柜子的棱长长 2 dm的8个正方体柜子的全部外表面,你能算出妈妈房间柜子的棱长吗?
解:设妈妈房间柜子的棱长为x dm,
则大桶油漆要刷的每个正方体柜子的表面积为 6(x+2)2 dm2,
根据一桶油漆可刷的面积,列出方程 8×6 (x+2)2 = 2400.
整理,得 (x+2)2= 50 .
这个方程可以直接开平方吗?
对照 x2 = 25的解法,试一试怎样解方程 (x+2)2= 50
将x+2看成一个整体
解: (x+2)2=50
直接开平方得
即
解得
一元二次方程
一元一次方程
降次
从以上的解法中,你发现了什么?
思考
一元二次方程
(代数式)2=常数
一元一次方程
转化
开平方
降次
解一元二次方程的思路是将方程转化为 ( x + m )2 = p的形式,它的一边是一个完全平方式,另一边是一个常数,当 p ≥ 0 时,两边同时开平方,转化为一元一次方程,便可求出它的根.
方法总结
用直接开平方法解一元二次方程的步骤:
(1)将方程化为x2=p或(mx+n)2=p ( p ≥ 0,m≠0)的形式;
(2)直接开平方化为两个一元一次方程;
(3)解两个一元一次方程得到原方程的解.
(1) 2x2 - 900=x2;
解:(1)移项,得
x2 = 900.
直接开平方,得
x = ±30,
即x1=30,x2=-30.
例 用直接开平方法解下列方程:
(2) x - 6x + 9 =16.
解:(2) x - 6x+9 = (x - 3) = 16
直接开平方,得
x - 3 = ±4 ,
即x1= 7
,x2= -1 .
1. 如图,这是一个简单的数值运算程序,则输入 x 的值为( )
A.x1=2,x2=﹣2 B.x1=3,x2=﹣3
C.x1=3,x2=﹣1 D.x1=﹣3,x2=1
C
2.对于一元二次方程x2=m-1.
(1)若方程有两个不相等的实数根,则m________;
(2)若方程有两个相等的实数根,则m________;
(3)若方程无实数根,则m________.
m-1>0
>1
m-1= 0
=1
m-1< 0
<1
(1) (x+1)2 - 3 = 2 ;
3. 计算:
(2) 2x2-8=-10;
解:
(2)移项,得2x2 = - 2,
系数化为1,得x2 = - 1,
因为-1无法开平方,所以方程无解.
解:(1) 移项,得 (x + 1) =5,
直接开平方得:
即x1=
,x2= .
x+1= ,
(3)(2x-1)2=(x-2)2 ;
3. 计算:
解:(3)直接开平方得:
2x-1= ,
即 2x-1=±(x-2) ,
∴2x-1=x-2或 2x-1 = - x+2 ,
即x1=-1,x2=1.
(4) x2 - x + 6 = 0 .
解:(4)x2 - x + 6
= ( x - )2 = 0.
直接开平方得:x - = 0
即x1 = x2= .
4. (新定义运算)在实数范围内定义运算“ ”,其法则为:a b = a2 - b2,求方程(4 3) x = 24的解.
解:∵a b = a2 - b2,
∴(4 3) x = (42 - 32) x = 7 x = 72 - x2,
∴ 72 - x2 = 24,
∴ x2 = 25,
∴ x = ±5.
利用平方根的意义直接开平方来求一元二次方程的解的方法叫做直接开平方法.
直接开
平方法
方程x2=p的
根的情况
概念
(1)将方程化为x2=p或(mx+n)2=p(p≥0,m≠0)的形式;
(2)直接开平方化为两个一元一次方程;
(3)解两个一元一次方程得到原方程的解.
步骤
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
