1.1 课时1 几何体的认识 课件(共22张PPT)2025-2026学年数学北师大版(2024)七年级上册
文档属性
| 名称 | 1.1 课时1 几何体的认识 课件(共22张PPT)2025-2026学年数学北师大版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 06:02:38 | ||
图片预览






文档简介
(共22张PPT)
课时1 几何体的认识
第一章 丰富的图形世界
1.1 生活中的立体图形
1.在具体情境中认识圆柱、圆锥、棱柱、球等常见的几何体,并能描述它们的基本特征.
2.通过认识常见几何体的特征,初步形成空间观念,感受图形世界的丰富多彩.
观察周围的世界,你会看到许许多多的图形。你能从中发现哪些熟悉的图形
以下常见物体的形状跟哪些几何体类似?
圆柱
圆锥
正方体
长方体
棱柱
球
探究点 1 常见的几何体及其分类
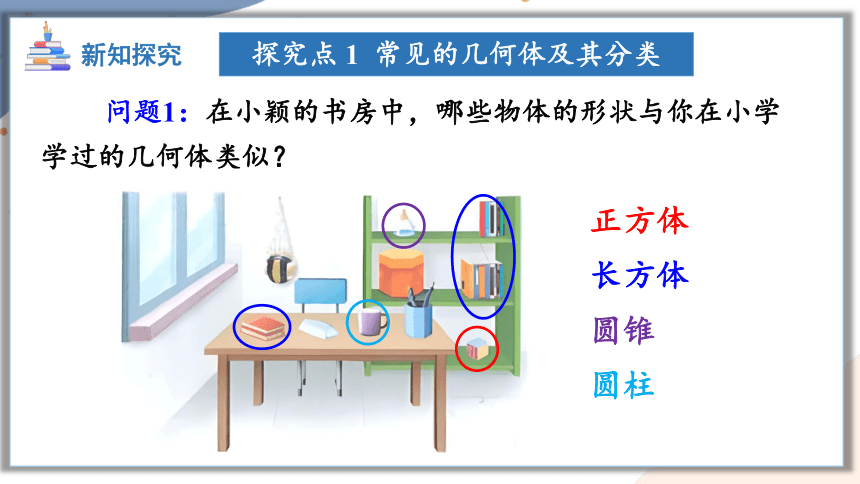
问题1:在小颖的书房中,哪些物体的形状与你在小学学过的几何体类似?
正方体
长方体
圆锥
圆柱
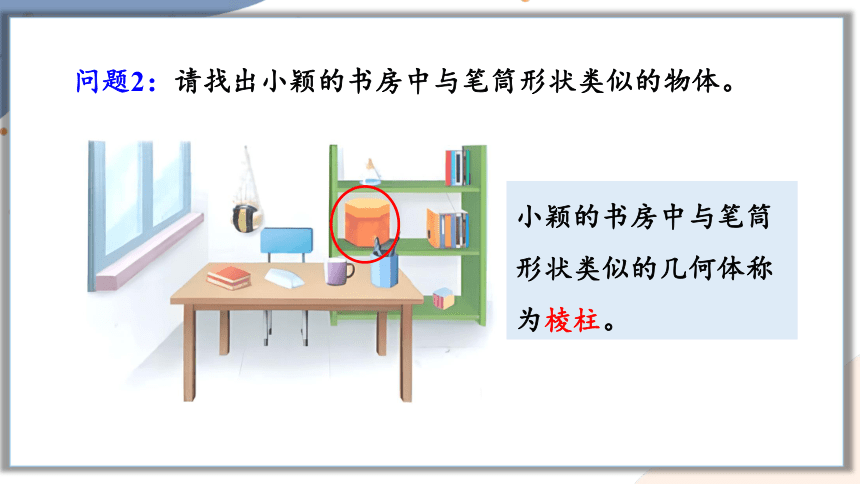
问题2:请找出小颖的书房中与笔筒形状类似的物体。
小颖的书房中与笔筒形状类似的几何体称为棱柱。
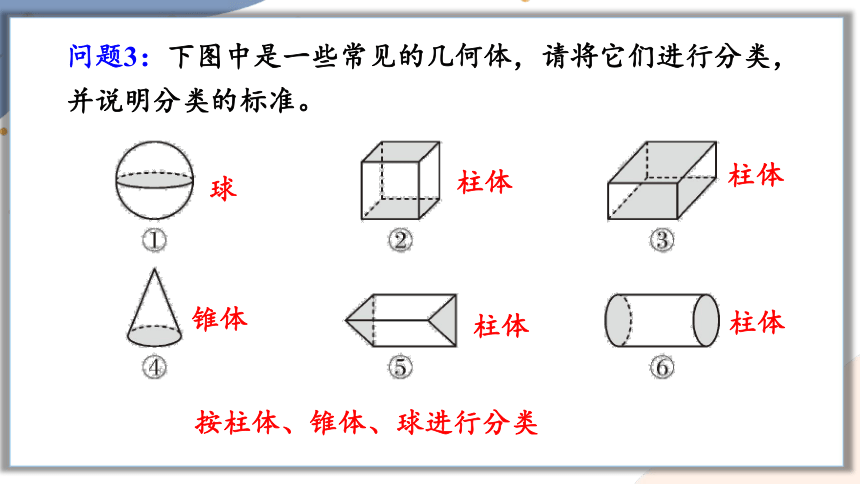
问题3:下图中是一些常见的几何体,请将它们进行分类,并说明分类的标准。
按柱体、锥体、球进行分类
球
柱体
锥体
柱体
柱体
柱体
1. 与图中实物图相类似的立体图形按从左至右的顺序依次是( )
A. 圆柱、圆锥、正方体、长方体
B. 圆柱、球、正方体、长方体
C. 棱柱、球、正方体、棱柱
D. 棱柱、圆锥、棱柱、长方体
B
练一练
2. 说一说生活中哪些物体的形状分别类似于棱柱、圆柱、圆锥与球。
练一练
问题1:下图中指出了六棱柱的顶点、侧棱、侧面和底面,请你指出图中其他棱柱的顶点、侧棱、侧面和底面。
三棱柱
四棱柱
五棱柱
六棱柱
底面
顶点
侧棱
侧面
探究点 2 棱柱的特征
三棱柱
底面
顶点
侧棱
侧面
四棱柱
底面
顶点
侧棱
侧面
五棱柱
底面
顶点
侧棱
侧面
在棱柱中,相邻两个面的交线叫作棱,相邻两个侧面的交线叫作侧棱。
问题2:通过对上面几个棱柱的观察,小组内合作、交流,指出棱柱的侧棱、侧面和底面分别有什么特点?
侧棱长相等,上下底面形状相同,
侧面的形状是平行四边形。
三棱柱
四棱柱
五棱柱
六棱柱
问题3:图中三棱柱、四棱柱、五棱柱、六棱柱的底面分别是什么图形? 据此你认为棱柱是怎么命名的?
三棱柱
四棱柱
五棱柱
六棱柱
三角形
四边形
五边形
六边形
命名规则:棱柱是按底面图形的边数来命名的。
问题4:棱柱可以分为直棱柱和斜棱柱(如图),观察这两种棱柱,它们有什么区别?
侧面是
侧面是
本书只讨论直棱柱
(简称棱柱)
直棱柱
斜棱柱
平行四边形
长方形
问题5:小组内讨论,总结出棱柱与圆柱的相同点与不同点。
几何体 图形 不同点 相同点
底面 侧面 顶点 棱
n棱柱
圆柱
n边形
圆
n个平的面
1个曲的面
2n个
无
3n条
无
都有两个底面,
并且两个底面
是形状、大小相同且相互平行的图形
例 下面物体可以近似地看成由一些常见几何体组合而成,你能找出其中常见的几何体吗?你还能举出其他组合几何体的例子吗?
圆锥、圆柱
棱锥、棱柱
圆柱、球
1. 将下列几何体分类.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
解法1:按照柱体、锥体、球可以分为三类:
柱体:
锥体:
球:
(1)、(2)、(4)、(6)、(7)
(5)
(3)
1. 将下列几何体分类.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
解法2:按照有无曲面分为两类:
有曲面:
无曲面:
(3)、(4)、(5)
(1)、(2)、(6)、(7)
2. 八棱柱的面的个数为 ,顶点个数为 ,棱的条数为 .
3. 若一个棱柱有12个顶点,且所有侧棱长的和为30 cm,则
每条侧棱长为 cm.
10
5
16
24
4.如图所示是一个六棱柱,它的底面边长都是4 cm,高是6 cm.
(1)这个棱柱共有多少条棱?所有的棱长的和是多少?
解:这个棱柱共有6+6+6=18(条)棱,
所有的棱长的和是12×4+6×6=84(cm).
(2)这个棱柱所有侧面的面积之和是多少?
解:S侧=4×6×6=144(cm2).
几何体
的认识
常见的几何体
棱柱
棱柱、圆柱、棱锥、圆锥、球等
特征
按柱体、锥体、球分类
所有侧棱长都相等
上、下底面的形状相同
侧面的形状都是平行四边形
棱柱与圆柱的异同
按有无曲的面分类
按有无顶点分类
课时1 几何体的认识
第一章 丰富的图形世界
1.1 生活中的立体图形
1.在具体情境中认识圆柱、圆锥、棱柱、球等常见的几何体,并能描述它们的基本特征.
2.通过认识常见几何体的特征,初步形成空间观念,感受图形世界的丰富多彩.
观察周围的世界,你会看到许许多多的图形。你能从中发现哪些熟悉的图形
以下常见物体的形状跟哪些几何体类似?
圆柱
圆锥
正方体
长方体
棱柱
球
探究点 1 常见的几何体及其分类
问题1:在小颖的书房中,哪些物体的形状与你在小学学过的几何体类似?
正方体
长方体
圆锥
圆柱
问题2:请找出小颖的书房中与笔筒形状类似的物体。
小颖的书房中与笔筒形状类似的几何体称为棱柱。
问题3:下图中是一些常见的几何体,请将它们进行分类,并说明分类的标准。
按柱体、锥体、球进行分类
球
柱体
锥体
柱体
柱体
柱体
1. 与图中实物图相类似的立体图形按从左至右的顺序依次是( )
A. 圆柱、圆锥、正方体、长方体
B. 圆柱、球、正方体、长方体
C. 棱柱、球、正方体、棱柱
D. 棱柱、圆锥、棱柱、长方体
B
练一练
2. 说一说生活中哪些物体的形状分别类似于棱柱、圆柱、圆锥与球。
练一练
问题1:下图中指出了六棱柱的顶点、侧棱、侧面和底面,请你指出图中其他棱柱的顶点、侧棱、侧面和底面。
三棱柱
四棱柱
五棱柱
六棱柱
底面
顶点
侧棱
侧面
探究点 2 棱柱的特征
三棱柱
底面
顶点
侧棱
侧面
四棱柱
底面
顶点
侧棱
侧面
五棱柱
底面
顶点
侧棱
侧面
在棱柱中,相邻两个面的交线叫作棱,相邻两个侧面的交线叫作侧棱。
问题2:通过对上面几个棱柱的观察,小组内合作、交流,指出棱柱的侧棱、侧面和底面分别有什么特点?
侧棱长相等,上下底面形状相同,
侧面的形状是平行四边形。
三棱柱
四棱柱
五棱柱
六棱柱
问题3:图中三棱柱、四棱柱、五棱柱、六棱柱的底面分别是什么图形? 据此你认为棱柱是怎么命名的?
三棱柱
四棱柱
五棱柱
六棱柱
三角形
四边形
五边形
六边形
命名规则:棱柱是按底面图形的边数来命名的。
问题4:棱柱可以分为直棱柱和斜棱柱(如图),观察这两种棱柱,它们有什么区别?
侧面是
侧面是
本书只讨论直棱柱
(简称棱柱)
直棱柱
斜棱柱
平行四边形
长方形
问题5:小组内讨论,总结出棱柱与圆柱的相同点与不同点。
几何体 图形 不同点 相同点
底面 侧面 顶点 棱
n棱柱
圆柱
n边形
圆
n个平的面
1个曲的面
2n个
无
3n条
无
都有两个底面,
并且两个底面
是形状、大小相同且相互平行的图形
例 下面物体可以近似地看成由一些常见几何体组合而成,你能找出其中常见的几何体吗?你还能举出其他组合几何体的例子吗?
圆锥、圆柱
棱锥、棱柱
圆柱、球
1. 将下列几何体分类.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
解法1:按照柱体、锥体、球可以分为三类:
柱体:
锥体:
球:
(1)、(2)、(4)、(6)、(7)
(5)
(3)
1. 将下列几何体分类.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
解法2:按照有无曲面分为两类:
有曲面:
无曲面:
(3)、(4)、(5)
(1)、(2)、(6)、(7)
2. 八棱柱的面的个数为 ,顶点个数为 ,棱的条数为 .
3. 若一个棱柱有12个顶点,且所有侧棱长的和为30 cm,则
每条侧棱长为 cm.
10
5
16
24
4.如图所示是一个六棱柱,它的底面边长都是4 cm,高是6 cm.
(1)这个棱柱共有多少条棱?所有的棱长的和是多少?
解:这个棱柱共有6+6+6=18(条)棱,
所有的棱长的和是12×4+6×6=84(cm).
(2)这个棱柱所有侧面的面积之和是多少?
解:S侧=4×6×6=144(cm2).
几何体
的认识
常见的几何体
棱柱
棱柱、圆柱、棱锥、圆锥、球等
特征
按柱体、锥体、球分类
所有侧棱长都相等
上、下底面的形状相同
侧面的形状都是平行四边形
棱柱与圆柱的异同
按有无曲的面分类
按有无顶点分类
同课章节目录
