5.4.2 二项式系数的性质(教学课件)__高二数学北师大(2019)选择性必修第一册(共28页PPT)
文档属性
| 名称 | 5.4.2 二项式系数的性质(教学课件)__高二数学北师大(2019)选择性必修第一册(共28页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 20:30:38 | ||
图片预览








文档简介
(共28张PPT)
5.4.2 二项式系数的性质
学习目标
1.了解杨辉三角,会用杨辉三角求二项式乘方次数较小时的各项的二项式系数,体现逻辑推理能力(重点)
2.理解二项式系数的性质并灵活运用,体现数学运算能力(难点)
新课导入
被誉为“世界七大奇迹”之一的古埃及的金字塔,以其宏伟的气势、严密的结构、精美绝伦的整体外观让世界叹服.而数学上也有“金字塔”,这就是二项式(a+b)n的展开式在n=1,2,…时的二项式系数而垒成的金字塔,称为杨辉三角,它是我国南宋数学家杨辉首先发现的,比欧洲的帕斯卡整整早发现了500年左右.
这节课我们将学习杨辉三角的规律.
新课学习
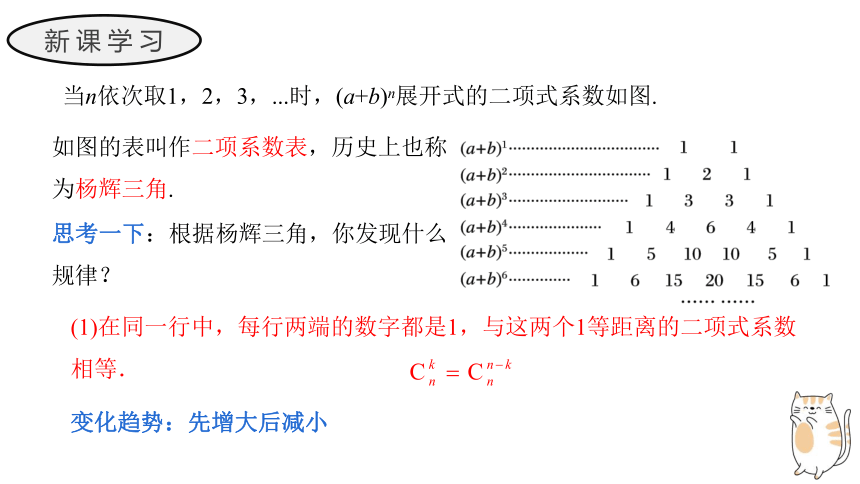
当n依次取1,2,3,...时,(a+b)n展开式的二项式系数如图.
如图的表叫作二项系数表,历史上也称为杨辉三角.
思考一下:根据杨辉三角,你发现什么规律?
(1)在同一行中,每行两端的数字都是1,与这两个1等距离的二项式系数相等.
变化趋势:先增大后减小
新课学习
思考一下:根据杨辉三角,你发现什么规律?
(2)在相邻的两行中,除1以外的每一个数都等于它"肩上"两个数的和(由组合数的性质:
即得); 当二项式的次数不大时,可借助杨辉三角直接写出各项的二项式系数.
新课学习
思考一下:二项式系数有什么性质?
1.各二项式系数的和
(1)在二项式定理中,令a=b=1,则有
这表明在二项展开式中各项的二项式系数之和为2.即
(与a,b的值无关,只与n的值有关)
新课学习
思考一下:二项式系数有什么性质?
1.各二项式系数的和
(2)在二项式定理中,令a=1,b=-1,则有
这表明在二项展开式中奇数项的二项式系数之和与偶数项的二项式系数之和相等且都等于2n-1.即
新课学习2.对称性思考一下:二项式系数有什么性质?与首末两端“等距离”的两项的二项式系数相等的直线将函数f(k)=的图象分成对称的两部分,它是图象的对称轴.1 11 2 11 3 3 11 4 6 4 11 5 10 10 5 11 6 15 20 15 6 1
新课学习
思考一下:二项式系数有什么性质?
3.增减性与最大值
因为
即
当
,即 时, 随k的增加而增加;
由对称性知, 时, 随k的增加而减小.
新课学习
思考一下:二项式系数有什么性质?
3.增减性与最大值
当n是偶数时,中间的一项 取得最大值;
当n是奇数时,中间的两项 和 相等,且同时取得最大值.
新课学习
例1:根据杨辉三角,写出(a+b)7展开式的二项式系数.
从图中的杨辉三角知道,展开式的二项式系数分别为1,6,15,20,15,6,1 ,根据其规律,有
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
所以(a+b)7展开式的二项式系数分别为1,7,21,35,35,21,7,1
于是,可以根据杨辉三角将二项式系数表延伸下去,从而可根据这个表来求二项式系数.
课堂巩固
例2:求证:
由二项式定理,有
令a=b=1, 则
新课学习
练一练:若 展开式前三项的二项式系数之和为22.
(1)求展开式中二项式系数最大的项及所有二项式系数和;
由题意可知,
即
得n=6或n=7(舍),
则展开式中最大的二项式系数为 ,
所以展开式中二项式系数最大的项为第4项,
即
所有二项式系数和为26=64.
新课学习
(2)求展开式中的常数项.
令
得r=4 ,
则
故展开式中的常数项为135.
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
60
课堂巩固
课堂总结
1.杨辉三角
2.二项式系数的性质
THANK YOU
5.4.2 二项式系数的性质
学习目标
1.了解杨辉三角,会用杨辉三角求二项式乘方次数较小时的各项的二项式系数,体现逻辑推理能力(重点)
2.理解二项式系数的性质并灵活运用,体现数学运算能力(难点)
新课导入
被誉为“世界七大奇迹”之一的古埃及的金字塔,以其宏伟的气势、严密的结构、精美绝伦的整体外观让世界叹服.而数学上也有“金字塔”,这就是二项式(a+b)n的展开式在n=1,2,…时的二项式系数而垒成的金字塔,称为杨辉三角,它是我国南宋数学家杨辉首先发现的,比欧洲的帕斯卡整整早发现了500年左右.
这节课我们将学习杨辉三角的规律.
新课学习
当n依次取1,2,3,...时,(a+b)n展开式的二项式系数如图.
如图的表叫作二项系数表,历史上也称为杨辉三角.
思考一下:根据杨辉三角,你发现什么规律?
(1)在同一行中,每行两端的数字都是1,与这两个1等距离的二项式系数相等.
变化趋势:先增大后减小
新课学习
思考一下:根据杨辉三角,你发现什么规律?
(2)在相邻的两行中,除1以外的每一个数都等于它"肩上"两个数的和(由组合数的性质:
即得); 当二项式的次数不大时,可借助杨辉三角直接写出各项的二项式系数.
新课学习
思考一下:二项式系数有什么性质?
1.各二项式系数的和
(1)在二项式定理中,令a=b=1,则有
这表明在二项展开式中各项的二项式系数之和为2.即
(与a,b的值无关,只与n的值有关)
新课学习
思考一下:二项式系数有什么性质?
1.各二项式系数的和
(2)在二项式定理中,令a=1,b=-1,则有
这表明在二项展开式中奇数项的二项式系数之和与偶数项的二项式系数之和相等且都等于2n-1.即
新课学习2.对称性思考一下:二项式系数有什么性质?与首末两端“等距离”的两项的二项式系数相等的直线将函数f(k)=的图象分成对称的两部分,它是图象的对称轴.1 11 2 11 3 3 11 4 6 4 11 5 10 10 5 11 6 15 20 15 6 1
新课学习
思考一下:二项式系数有什么性质?
3.增减性与最大值
因为
即
当
,即 时, 随k的增加而增加;
由对称性知, 时, 随k的增加而减小.
新课学习
思考一下:二项式系数有什么性质?
3.增减性与最大值
当n是偶数时,中间的一项 取得最大值;
当n是奇数时,中间的两项 和 相等,且同时取得最大值.
新课学习
例1:根据杨辉三角,写出(a+b)7展开式的二项式系数.
从图中的杨辉三角知道,展开式的二项式系数分别为1,6,15,20,15,6,1 ,根据其规律,有
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
所以(a+b)7展开式的二项式系数分别为1,7,21,35,35,21,7,1
于是,可以根据杨辉三角将二项式系数表延伸下去,从而可根据这个表来求二项式系数.
课堂巩固
例2:求证:
由二项式定理,有
令a=b=1, 则
新课学习
练一练:若 展开式前三项的二项式系数之和为22.
(1)求展开式中二项式系数最大的项及所有二项式系数和;
由题意可知,
即
得n=6或n=7(舍),
则展开式中最大的二项式系数为 ,
所以展开式中二项式系数最大的项为第4项,
即
所有二项式系数和为26=64.
新课学习
(2)求展开式中的常数项.
令
得r=4 ,
则
故展开式中的常数项为135.
课堂巩固
A
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
60
课堂巩固
课堂总结
1.杨辉三角
2.二项式系数的性质
THANK YOU
同课章节目录
