6.1.1 条件概率的概念(教学课件)__高二数学北师大(2019)选择性必修第一册(共33页PPT)
文档属性
| 名称 | 6.1.1 条件概率的概念(教学课件)__高二数学北师大(2019)选择性必修第一册(共33页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 20:31:23 | ||
图片预览











文档简介
(共33张PPT)
6.1.1 条件概率的概念
学习目标
1.结合古典概型,了解条件概率的定义,体现逻辑推理能力(重点)
2.掌握条件概率的计算方法,体现数学运算能力(重点)
3.利用条件概率公式解决一些简单的实际问题,体现数学运算能力(难点)
新课导入
复习一下:什么是古典概率模型的概念?
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型.
那么,如何利用古典概率求下面问题的概率呢?
新课学习
问题1:三张奖券中只有一张能中奖,现分别由三名同学不放回地抽取,那么最后一名同学中奖的概率是否比前两位小?
分析:在3名同学抽取奖券的试验中,设事件Y表示“抽到中奖奖券”,事件N1,N2分别表示“抽到未中奖奖券1”“抽到未中奖奖券2”,则该试验的样本空间为Ω={YN1N2,YN2N1,N1YN2,N2YN1,N1N2Y,N2N1Y}.
事件B表示“最后一名同学抽到中奖奖券”,则B={N1N2Y,N2N1Y},
由古典概型概率公式,P(B)=
其中,n(B)和n(Ω)分别表示事件B和样本空间Ω包含的样本点个数.
新课学习
问题1:三张奖券中只有一张能中奖,现分别由三名同学不放回地抽取,那么最后一名同学中奖的概率是否比前两位小?
这说明最后一名同学抽到中奖奖券的概率不比其他同学的小.事实上,我们之前也研究过抽签问题,知道抽签虽有先后,但抽签是公平的,即每个人抽到中奖奖券的概率相等.
新课学习
问题2:继续考虑上面的问题,如果已知第一名同学没有抽到中奖奖券,那么最后一名同学抽到中奖奖券的概率又是多少呢?
分析:用事件A表示"第一名同学未抽到中奖奖券", 事件B表示 "最后一名同学抽到中奖奖券",则A={N1YN2,N2YN1,N1N2Y,N2N1Y},B={N1N2Y,N2N1Y}.
第一名同学没有抽到中奖奖券,所以此时样本点的个数由原来的6个减少为4个.
由古典概型计算概率的公式可知,如果已知第一名同学没有抽到中奖奖券,那么最后一名同学抽到中奖奖券的概率为 ,即 .
显然, 知道第一名同学的抽取结果, 即知道了事件A的发生与否,会影响事件B发生的概率.
新课学习
问题3:知道第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
分析:因为已经知道事件A发生,所以只需局限在事件A发生的范围内考虑问题, 即样本空间Ω由缩小为A.
此外,在事件A发生的情况下事件B发生,等价于事件A和事件B同时发生,即原来的事件B缩小为AB. 因此相应的概率会发生变化.
新课学习
问题4:如何计算在事件A发生的情况下事件B发生的概率呢?
以古典概型为例. 由于样本空间由Ω缩小为A,同时原来的事件B缩小为AB,因此在事件A发生的情况下事件B发生的概率为
其中,n(A),n(AB)和n(Ω)分别表示事件A、事件AB和样本空间Ω包含的样本点个数.
新课学习
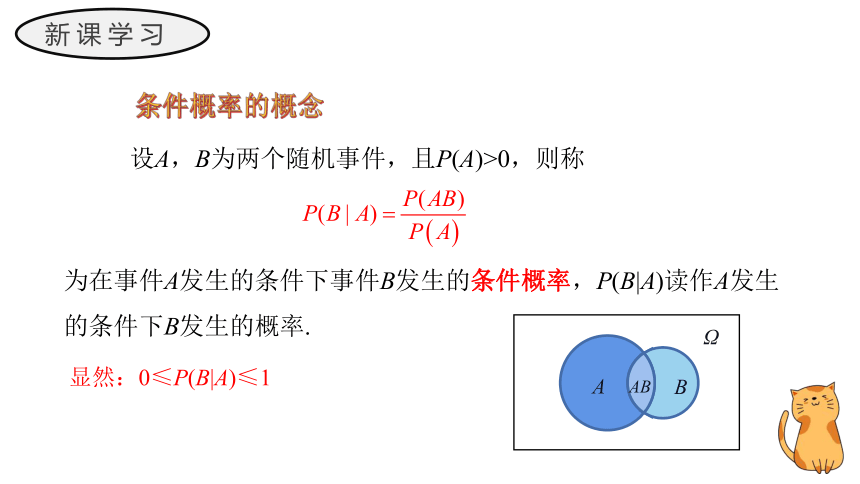
条件概率的概念
设A,B为两个随机事件,且P(A)>0,则称
为在事件A发生的条件下事件B发生的条件概率,P(B|A)读作A发生的条件下B发生的概率.
显然:0≤P(B|A)≤1
A
B
AB
Ω
新课学习
思考一下:怎么从集合的角度来看条件概率?
从集合的角度看,若事件A已发生,则为使B也发生,试验结果必须是既在A中又在B中的样本点, 即此点必属于AB (如图).
由于已知A已经发生, 故A成为计算条件概率P(B|A)新的样本空间.
新课学习
条件概率的性质
设P(A)>0,则
(1)P(Ω|A)=1;
(2)如果B,C是两个互斥事件,则P(B∪C | A)=P(B|A)+P(C|A);
(3)设和B互为对立事件,则
新课学习
思考交流:概率P(B|A)与P(AB)有什么区别和联系?
区别:P(B|A)是在事件A发生的条件下事件B发生的概率,P(AB)是事件A,B同时发生的概率.
联系:事件A,B 都发生.
新课学习
思考交流:若B和C是两个互斥事件,则P[(B∪C)|A]=P(B|A)+P(C|A)是否成立?
因为B和C是两个互斥事件,
所以P[(B∪C)|A]=
=P(B|A)+P(C|A)
所以P[(B∪C)|A]=P(B|A)+P(C|A)成立.
新课学习
例1:在5道题中有3道选择题和2道填空题.如果不放回地依次抽取2道题,求:
(1)第一次抽到选择题的概率;
设事件A=“第一次抽到选择题”,事件B=“第二次抽到选择题”,则事件AB=“第一次和第二次都抽到选择题”.
样本空间包含的样本点个数为:n(Ω)= =20.
由分步乘法计数原理,得
于是
新课学习
(2)第一次和第二次都抽到选择题的概率;
因为n(AB)= =6,所以
新课学习
(3)在第一次抽到选择题的条件下,第二次抽到选择题的概率.
方法1:由(1)(2)可知P(A)= P(AB)= 所以
故在第一次抽到选择题的条件下,第二次抽到选择题的概率为
方法2:由(1)(2)可知n(AB)=6,n(AB)=12,所以
故在第一次抽到选择题的条件下,第二次抽到选择题的概率为
新课学习
思考一下:计算条件概率有什么方法?
(1)在样本空间Ω中,先求概率P(AB)和P(A),再按定义计算P(B|A);
(2)随机事件A的样本点构成了一个小样本空间A,在样本空间A中求事件B的概率,就得到P(B|A).
新课学习
例2:一张储蓄卡的密码共有6位数字,每位数字都可从0-9中任选一个.某人在银行自动取款机上取钱时,忘记了密码的最后一位数字.求:
(1)任意按最后一位数字,不超过两次就按对的概率;
设事件Ai(i=1,2)=“第i次按对密码”,事件A=“不超过两次就按对密码”,则
依题意知事件A1与事件 互斥,由概率的加法公式得
故任意按最后一位数字,不超过两次就按对的概率为
新课学习
(2)如果他记得密码的最后一位是偶数,不超过两次就按对的概率.
设事件B=“密码的最后一位数字按偶数”,则
P(A|B)=
故如果他记得密码的最后一位是偶数,不超过两次就按对的概率为
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
0.75
课堂巩固
课堂总结
1.条件概率的概念
2.条件概率的性质
THANK YOU
6.1.1 条件概率的概念
学习目标
1.结合古典概型,了解条件概率的定义,体现逻辑推理能力(重点)
2.掌握条件概率的计算方法,体现数学运算能力(重点)
3.利用条件概率公式解决一些简单的实际问题,体现数学运算能力(难点)
新课导入
复习一下:什么是古典概率模型的概念?
(1)有限性:样本空间的样本点只有有限个;
(2)等可能性:每个样本点发生的可能性相等.
我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型.
那么,如何利用古典概率求下面问题的概率呢?
新课学习
问题1:三张奖券中只有一张能中奖,现分别由三名同学不放回地抽取,那么最后一名同学中奖的概率是否比前两位小?
分析:在3名同学抽取奖券的试验中,设事件Y表示“抽到中奖奖券”,事件N1,N2分别表示“抽到未中奖奖券1”“抽到未中奖奖券2”,则该试验的样本空间为Ω={YN1N2,YN2N1,N1YN2,N2YN1,N1N2Y,N2N1Y}.
事件B表示“最后一名同学抽到中奖奖券”,则B={N1N2Y,N2N1Y},
由古典概型概率公式,P(B)=
其中,n(B)和n(Ω)分别表示事件B和样本空间Ω包含的样本点个数.
新课学习
问题1:三张奖券中只有一张能中奖,现分别由三名同学不放回地抽取,那么最后一名同学中奖的概率是否比前两位小?
这说明最后一名同学抽到中奖奖券的概率不比其他同学的小.事实上,我们之前也研究过抽签问题,知道抽签虽有先后,但抽签是公平的,即每个人抽到中奖奖券的概率相等.
新课学习
问题2:继续考虑上面的问题,如果已知第一名同学没有抽到中奖奖券,那么最后一名同学抽到中奖奖券的概率又是多少呢?
分析:用事件A表示"第一名同学未抽到中奖奖券", 事件B表示 "最后一名同学抽到中奖奖券",则A={N1YN2,N2YN1,N1N2Y,N2N1Y},B={N1N2Y,N2N1Y}.
第一名同学没有抽到中奖奖券,所以此时样本点的个数由原来的6个减少为4个.
由古典概型计算概率的公式可知,如果已知第一名同学没有抽到中奖奖券,那么最后一名同学抽到中奖奖券的概率为 ,即 .
显然, 知道第一名同学的抽取结果, 即知道了事件A的发生与否,会影响事件B发生的概率.
新课学习
问题3:知道第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
分析:因为已经知道事件A发生,所以只需局限在事件A发生的范围内考虑问题, 即样本空间Ω由缩小为A.
此外,在事件A发生的情况下事件B发生,等价于事件A和事件B同时发生,即原来的事件B缩小为AB. 因此相应的概率会发生变化.
新课学习
问题4:如何计算在事件A发生的情况下事件B发生的概率呢?
以古典概型为例. 由于样本空间由Ω缩小为A,同时原来的事件B缩小为AB,因此在事件A发生的情况下事件B发生的概率为
其中,n(A),n(AB)和n(Ω)分别表示事件A、事件AB和样本空间Ω包含的样本点个数.
新课学习
条件概率的概念
设A,B为两个随机事件,且P(A)>0,则称
为在事件A发生的条件下事件B发生的条件概率,P(B|A)读作A发生的条件下B发生的概率.
显然:0≤P(B|A)≤1
A
B
AB
Ω
新课学习
思考一下:怎么从集合的角度来看条件概率?
从集合的角度看,若事件A已发生,则为使B也发生,试验结果必须是既在A中又在B中的样本点, 即此点必属于AB (如图).
由于已知A已经发生, 故A成为计算条件概率P(B|A)新的样本空间.
新课学习
条件概率的性质
设P(A)>0,则
(1)P(Ω|A)=1;
(2)如果B,C是两个互斥事件,则P(B∪C | A)=P(B|A)+P(C|A);
(3)设和B互为对立事件,则
新课学习
思考交流:概率P(B|A)与P(AB)有什么区别和联系?
区别:P(B|A)是在事件A发生的条件下事件B发生的概率,P(AB)是事件A,B同时发生的概率.
联系:事件A,B 都发生.
新课学习
思考交流:若B和C是两个互斥事件,则P[(B∪C)|A]=P(B|A)+P(C|A)是否成立?
因为B和C是两个互斥事件,
所以P[(B∪C)|A]=
=P(B|A)+P(C|A)
所以P[(B∪C)|A]=P(B|A)+P(C|A)成立.
新课学习
例1:在5道题中有3道选择题和2道填空题.如果不放回地依次抽取2道题,求:
(1)第一次抽到选择题的概率;
设事件A=“第一次抽到选择题”,事件B=“第二次抽到选择题”,则事件AB=“第一次和第二次都抽到选择题”.
样本空间包含的样本点个数为:n(Ω)= =20.
由分步乘法计数原理,得
于是
新课学习
(2)第一次和第二次都抽到选择题的概率;
因为n(AB)= =6,所以
新课学习
(3)在第一次抽到选择题的条件下,第二次抽到选择题的概率.
方法1:由(1)(2)可知P(A)= P(AB)= 所以
故在第一次抽到选择题的条件下,第二次抽到选择题的概率为
方法2:由(1)(2)可知n(AB)=6,n(AB)=12,所以
故在第一次抽到选择题的条件下,第二次抽到选择题的概率为
新课学习
思考一下:计算条件概率有什么方法?
(1)在样本空间Ω中,先求概率P(AB)和P(A),再按定义计算P(B|A);
(2)随机事件A的样本点构成了一个小样本空间A,在样本空间A中求事件B的概率,就得到P(B|A).
新课学习
例2:一张储蓄卡的密码共有6位数字,每位数字都可从0-9中任选一个.某人在银行自动取款机上取钱时,忘记了密码的最后一位数字.求:
(1)任意按最后一位数字,不超过两次就按对的概率;
设事件Ai(i=1,2)=“第i次按对密码”,事件A=“不超过两次就按对密码”,则
依题意知事件A1与事件 互斥,由概率的加法公式得
故任意按最后一位数字,不超过两次就按对的概率为
新课学习
(2)如果他记得密码的最后一位是偶数,不超过两次就按对的概率.
设事件B=“密码的最后一位数字按偶数”,则
P(A|B)=
故如果他记得密码的最后一位是偶数,不超过两次就按对的概率为
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
0.75
课堂巩固
课堂总结
1.条件概率的概念
2.条件概率的性质
THANK YOU
同课章节目录
