6.3.1 离散型随机变量的均值(教学课件)__高二数学北师大(2019)选择性必修第一册(共31页PPT)
文档属性
| 名称 | 6.3.1 离散型随机变量的均值(教学课件)__高二数学北师大(2019)选择性必修第一册(共31页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-02 20:35:16 | ||
图片预览











文档简介
(共31张PPT)
6.3.1 离散型随机变量的均值
学习目标
1.理解离散型随机变量的均值的含义,了解随机变量的均值与样本均值的区别与联系,体现逻辑推理能力(重点)
2.能计算简单离散型随机变量的均值,并能解决一些实际问题,体现数学计算能力(难点)
新课导入
回顾一下本章第2节中的例1:
已知在10件产品中有2件不合格品. 从这10件产品中任取3件, 用X表示取得产品中的不合格品的件数. 我们可求得X的分布列如表:
k 0 1 2
p
现在我们关心, 取 3 件该产品时, 平均会取到几件不合格品
那么, 怎样的一个数能够 "代表" 这个随机变量取值的平均水平呢
新课学习
分析上面的问题:
我们来看看一个常见的求平均值的问题.设有12个西瓜,其中有4个质量是5kg,3个质量是6kg,5个质量是7kg,求这12个西瓜的平均质量?
有平均数的意义,西瓜的平均质量应为12个西瓜的总重量除以西瓜的总个数,即
①式也可以写出如下的形式:
其中 , , 分别为质量是5kg,6kg,7kg的西瓜质量个数在西瓜总个数中所占的比例.②式告诉我们,如果我们知道各个质量所占的比例,则平均质量等于各个质量乘相应的比例,再求和.
新课学习
那么,前面“取不合格品的问题”中,根据X的分布列,有
③式表示,在一次抽取中,3件产品中平均有0.6件是不合格品.这样,平均数0.6就代表“取次品的问题”中随机变量X的平均取值.
新课学习
离散型随机变量X的均值的概念
设离散型随机变量X的分布列如下表:
X x1 x2 … xi … xn
p p1 p2 … pi … pn
则称为
EX=x1p1+x2p2+…+xipi+xnpn
为随机变量X的均值或者数学期望(简称期望).
新课学习
拓展:对离散型随机变量数学期望理解:
1.均值EX刻画的是X取值的“中心位置”,反映了离散型随机变量X取值的平均水平,是随机变量X的一个重要特征.
2.两个不同的分布可以有相同的均值.
3.均值EX是随机变量取各个值的加权平均,由X的分布列完全确定.
4.均值只是刻画了随机变量取值的“中心位置”这一重要特征,并不能完全决定随机变量的性质.
新课学习
思考一下:随机变量的均值与样本均值的联系与区别是什么?
区别:随机变量的均值是一个确定的数,而样本均值具有随机性,它围绕随机变量的均值波动.
联系:随着重复试验次数的增加,样本均值的波动幅度一般会越来越小.常用随机变量的观测值的均值去估计随机变量的均值.
新课学习
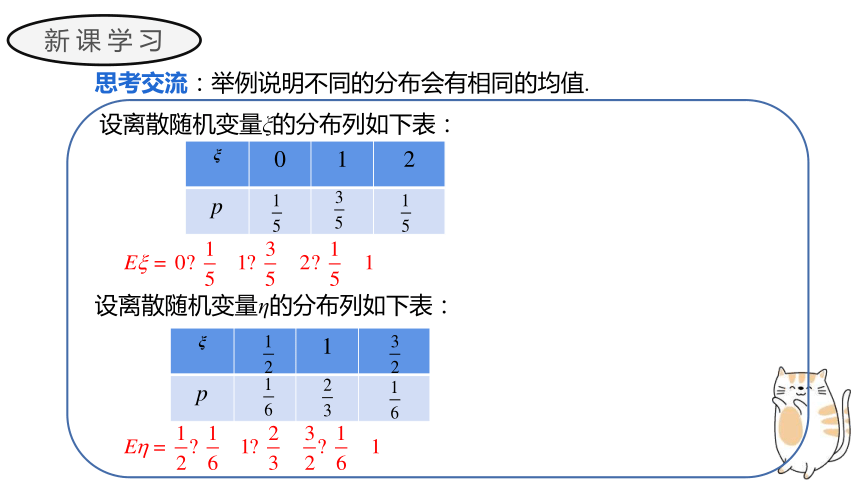
思考交流:举例说明不同的分布会有相同的均值.
设离散随机变量ξ的分布列如下表:
ξ 0 1 2
p
设离散随机变量η的分布列如下表:
ξ 1
p
新课学习
例1:设随机变量X服从参数为p的两点分布,求EX.
依题意知
EX=0·P(X=0)+1·P(X=1)
=0·(1-p)+1·p=p
因此,当X服从参数为p的两点分布时,其均值EX=p.
新课学习
例2:设X表示抛掷一枚均匀骰子掷出的点数,求EX.
依题意知X的分布列为
P(X=i)= (i=1,2,3,4,5,6)
如下表:
i 0 1 2 3 4 5 6
P(X=i)
根据均值的定义,可知
新课学习
思考交流:拋掷一枚均匀的骰子,掷出的点数只可能是1,2,3,4,5,6,怎样解释这个均值 呢
均值 ,指的是掷出的点数1,2,…,6的中心位置,反应了点数值的平均水平,是概率意义下的平均值,不是指某次投掷出现的结果.
新课学习
例3:一个袋子里装有除颜色外完全相同的3个红球和2个黄球,从中同时取出2个球,则取出的红球个数的均值是多少?
设X表示取出红球的个数,则X的取值为0,1,2.
故X的分布列如下表:
新课学习
例3:一个袋子里装有除颜色外完全相同的3个红球和2个黄球,从中同时取出2个球,则取出的红球个数的均值是多少?
X 0 1 2
P
根据均值的定义,可知
新课学习
思考一下:根据上面的例题,总结一下求离散型随机变量X的均值的步骤?
1.理解X的实际意义,写出X全部可能取值;
2.求出X取每个值时的概率;
3.写出X的分布列;
4.利用定义公式 求出均值.
新课学习
例4:根据气象预报,某地区近期暴发小洪水的概率为0.25,暴发大洪水的概率为0.01.该地区某工地上有一台大型设备,为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元.
方案2:建一保护围墙,建设费为2000元,但围墙只能防小洪水.
方案3:不采取措施,希望不发生洪水,此时遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.
你会选择哪一种方案呢?
新课学习
用X1,X2,X3和分别表示以上3种方案的损失
采用方案1,无论有无洪水,都损失3800元,即X1=3800,故EX1=3800(元)
采用方案2,遇到大洪水时,损失2000+60000=62000元;没有大洪水时,损失2000元.因此
EX2=62000×0.01+2000×(1-0.01)=2600(元)
采用方案3,遇到大洪水时,损失60000元;遇到小洪水时,损失10000元;无洪水时,损失为0元,因此
EX3=60000×0.01+10000×0.25+0×(1-0.01-0.25)=3100(元)
由此可见,就平均而言,方案2的损失最小.
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
0
课堂巩固
课堂总结
1.离散型随机变量X的均值概念
2.求离散型随机变量X的均值的步骤
THANK YOU
6.3.1 离散型随机变量的均值
学习目标
1.理解离散型随机变量的均值的含义,了解随机变量的均值与样本均值的区别与联系,体现逻辑推理能力(重点)
2.能计算简单离散型随机变量的均值,并能解决一些实际问题,体现数学计算能力(难点)
新课导入
回顾一下本章第2节中的例1:
已知在10件产品中有2件不合格品. 从这10件产品中任取3件, 用X表示取得产品中的不合格品的件数. 我们可求得X的分布列如表:
k 0 1 2
p
现在我们关心, 取 3 件该产品时, 平均会取到几件不合格品
那么, 怎样的一个数能够 "代表" 这个随机变量取值的平均水平呢
新课学习
分析上面的问题:
我们来看看一个常见的求平均值的问题.设有12个西瓜,其中有4个质量是5kg,3个质量是6kg,5个质量是7kg,求这12个西瓜的平均质量?
有平均数的意义,西瓜的平均质量应为12个西瓜的总重量除以西瓜的总个数,即
①式也可以写出如下的形式:
其中 , , 分别为质量是5kg,6kg,7kg的西瓜质量个数在西瓜总个数中所占的比例.②式告诉我们,如果我们知道各个质量所占的比例,则平均质量等于各个质量乘相应的比例,再求和.
新课学习
那么,前面“取不合格品的问题”中,根据X的分布列,有
③式表示,在一次抽取中,3件产品中平均有0.6件是不合格品.这样,平均数0.6就代表“取次品的问题”中随机变量X的平均取值.
新课学习
离散型随机变量X的均值的概念
设离散型随机变量X的分布列如下表:
X x1 x2 … xi … xn
p p1 p2 … pi … pn
则称为
EX=x1p1+x2p2+…+xipi+xnpn
为随机变量X的均值或者数学期望(简称期望).
新课学习
拓展:对离散型随机变量数学期望理解:
1.均值EX刻画的是X取值的“中心位置”,反映了离散型随机变量X取值的平均水平,是随机变量X的一个重要特征.
2.两个不同的分布可以有相同的均值.
3.均值EX是随机变量取各个值的加权平均,由X的分布列完全确定.
4.均值只是刻画了随机变量取值的“中心位置”这一重要特征,并不能完全决定随机变量的性质.
新课学习
思考一下:随机变量的均值与样本均值的联系与区别是什么?
区别:随机变量的均值是一个确定的数,而样本均值具有随机性,它围绕随机变量的均值波动.
联系:随着重复试验次数的增加,样本均值的波动幅度一般会越来越小.常用随机变量的观测值的均值去估计随机变量的均值.
新课学习
思考交流:举例说明不同的分布会有相同的均值.
设离散随机变量ξ的分布列如下表:
ξ 0 1 2
p
设离散随机变量η的分布列如下表:
ξ 1
p
新课学习
例1:设随机变量X服从参数为p的两点分布,求EX.
依题意知
EX=0·P(X=0)+1·P(X=1)
=0·(1-p)+1·p=p
因此,当X服从参数为p的两点分布时,其均值EX=p.
新课学习
例2:设X表示抛掷一枚均匀骰子掷出的点数,求EX.
依题意知X的分布列为
P(X=i)= (i=1,2,3,4,5,6)
如下表:
i 0 1 2 3 4 5 6
P(X=i)
根据均值的定义,可知
新课学习
思考交流:拋掷一枚均匀的骰子,掷出的点数只可能是1,2,3,4,5,6,怎样解释这个均值 呢
均值 ,指的是掷出的点数1,2,…,6的中心位置,反应了点数值的平均水平,是概率意义下的平均值,不是指某次投掷出现的结果.
新课学习
例3:一个袋子里装有除颜色外完全相同的3个红球和2个黄球,从中同时取出2个球,则取出的红球个数的均值是多少?
设X表示取出红球的个数,则X的取值为0,1,2.
故X的分布列如下表:
新课学习
例3:一个袋子里装有除颜色外完全相同的3个红球和2个黄球,从中同时取出2个球,则取出的红球个数的均值是多少?
X 0 1 2
P
根据均值的定义,可知
新课学习
思考一下:根据上面的例题,总结一下求离散型随机变量X的均值的步骤?
1.理解X的实际意义,写出X全部可能取值;
2.求出X取每个值时的概率;
3.写出X的分布列;
4.利用定义公式 求出均值.
新课学习
例4:根据气象预报,某地区近期暴发小洪水的概率为0.25,暴发大洪水的概率为0.01.该地区某工地上有一台大型设备,为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元.
方案2:建一保护围墙,建设费为2000元,但围墙只能防小洪水.
方案3:不采取措施,希望不发生洪水,此时遇到大洪水时要损失60000元,遇到小洪水时要损失10000元.
你会选择哪一种方案呢?
新课学习
用X1,X2,X3和分别表示以上3种方案的损失
采用方案1,无论有无洪水,都损失3800元,即X1=3800,故EX1=3800(元)
采用方案2,遇到大洪水时,损失2000+60000=62000元;没有大洪水时,损失2000元.因此
EX2=62000×0.01+2000×(1-0.01)=2600(元)
采用方案3,遇到大洪水时,损失60000元;遇到小洪水时,损失10000元;无洪水时,损失为0元,因此
EX3=60000×0.01+10000×0.25+0×(1-0.01-0.25)=3100(元)
由此可见,就平均而言,方案2的损失最小.
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
0
课堂巩固
课堂总结
1.离散型随机变量X的均值概念
2.求离散型随机变量X的均值的步骤
THANK YOU
同课章节目录
